長短波方程的兩個守恒型緊致有限差分格式
蔣佳平, 王廷春
(南京信息工程大學數學與統計學院,南京 210044)
1 引言
長短波方程是無窮維動力系統中一類重要的共振模型,用來描述流體力學中的長短波相互作用,也被用來描述重力和毛細管的波模型[1,2],此外,該方程的研究在等離子物理學[3]中也有廣泛應用.長短波方程在描述長波和短波的共振時,短波通常用薛定諤方程描述,而長波則常用帶有色散項的波方程描述[1],其數學形式為

其中參數λ, α, ε 是三個正常數,短波曲線u = u(x,t)是未知的復值函數,長波振幅v =v(x,t)為未知的實值函數,外力項f 和g 分別為已知的復值和實值函數,其在很多物理問題取值為零.我們考慮長短波(LS)方程的初邊值問題,其初邊值條件為

其中u0(x)和v0(x)分別為已知的復值和實值函數.
不難驗證,當外力項f(x,t)=0, g(x,t)=0 時,初值問題(1)–(4)滿足總質量與總能量守恒律
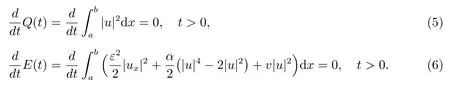
文獻[4–7]中已給出關于長短波方程初值問題的精確解及其性質的研究,其中Guo[5]討論了關于長短波方程的全局解,Tsutsumi 和Hatano[7]研究了關于長短波共振方程柯西問題的適定性.近年來,許多數值方法被用于求解長短波方程,其中包括有限元法、譜方法、有限差分法等.Liu 和Lv[8]提出了關于長短波方程的一類擬譜方法.Chang 等[9]也提出了一些數值格式,包括Crank-Nicolson 隱格式(CNI),三層Richardson 外推格式以及分裂步譜方法.由于高階緊致有限差分格式[10-16]通常能保持較高的精度和分辨率,經常被用來計算難以直接求解的偏微分方程(組).王蘭和段亞麗[10]首次對LS 方程給出了幾個高階緊致差分格式,包括一個能量守恒格式和幾個非守恒格式,所有格式對短波曲線函數的數值解在空間方向上都達到了四階收斂精度.本文在上述文獻的基礎上,進一步對LS 方程構造出兩個四階緊致有限差分格式,使短波曲線函數與長波振幅函數收斂精度在空間方向上均達到四階精度,時間方向達到二階精度,并且能在離散意義下保持原問題的兩個守恒性質.
本文的結構如下:在第2 部分中,我們提出了兩個關于LS 方程的緊致有限差分格式,并證明兩個格式在離散意義下均保持原問題的兩個守恒律.在第3 部分中,我們給出了幾個數值實驗,數值結果表明我們的格式在空間方向和時間方向分別具有四階和二階精度,同時驗證兩個格式都非常好地保持總質量和總能量守恒.在第4 部分中,我們給出了結論.
2 有限差分格式和守恒律
取空間步長和時間步長分別為h = (b ?a)/J 和τ = T/N,其中J 和N 是兩個正整數.令 (xj,tn) = (a+jh,nτ), j = 0,1,2,··· ,J, n = 0,1,2,··· ,N 為網格點.記分別為(u,v)在點(xj,tn)處的數值解和精確解,記分別為v 在點處的數值解和精確解.定義網格函數空間Xh為

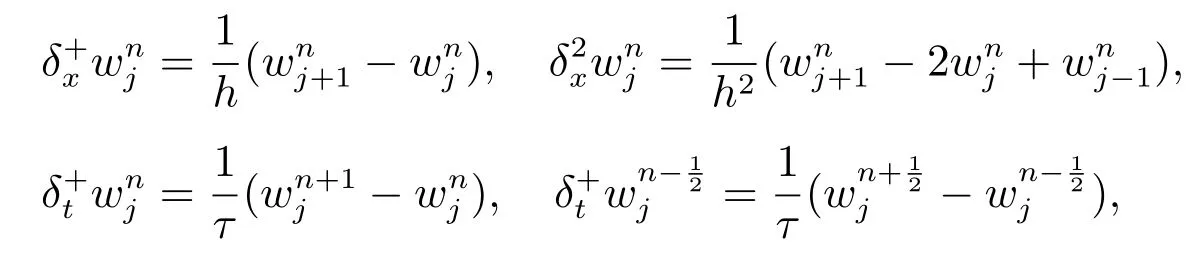

關于緊致算子Ah, Bh和負拉普拉斯算子,我們引入如下三個三對角矩陣

同時,有
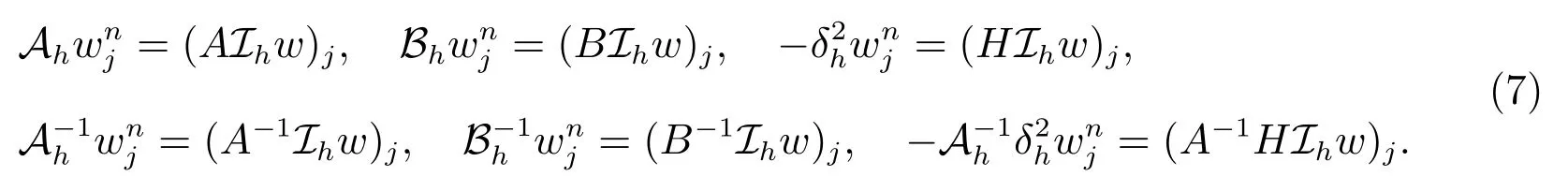
定義網格函數空間Xh中的離散內積和離散范數如下

本文需要用到如下引理:
引理1[16]對稱正定矩陣A, B 和H,我們有如下結論:
(a) 矩陣A, B 和H 是三個對稱正定矩陣,且具有如下特征

(b) 它們有相同的特征向量,即

由(7)及引理1,可得


引理2[16]對任何un∈ Xh, n=0,1,··· ,N,我們有
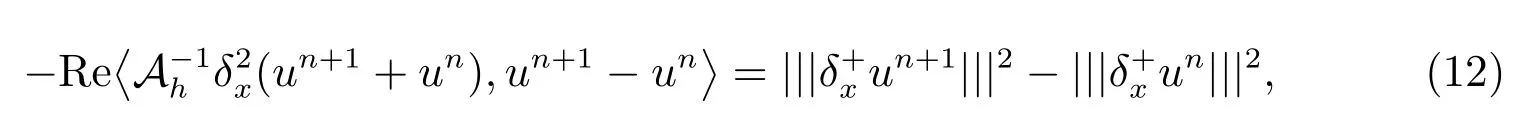
其中Re(w)表示w 的實部.
分別用緊致有限差分法和Crank-Nicolson 離散方法對未知函數在空間和時間兩個方向的導數進行離散,可得初邊值問題(1)–(4)的如下緊致有限差分格式,即:
格式1

格式2

與原問題(1)–(4)的齊次形式保持總質量和總能量守恒相對應,格式1 與格式2 在離散意義下也保持總質量和總能量守恒.
引理3格式1 在離散意義下保持原問題的兩個守恒性質,即總質量和總能量守恒

證明 將(13)式與Un+1+Un做內積并取虛部,可得
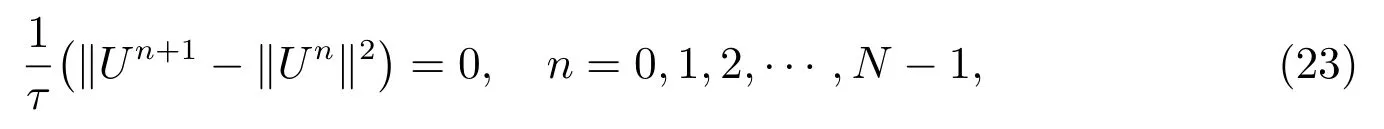
由此可得離散意義下的總質量守恒律(20).
將(13)式與Un+1?Un做內積,運用引理(8),取實部得

將(14)式與|Un+1|2?|Un|2做內積,可得

對于(25)式左邊部分,我們有

對于(25)式右邊部分,結合邊界條件,有

將(26)和(27)帶入(25),可得

將(28)和(24)分別乘以1/2 和2,然后將兩者相加可得

由此可得離散意義下的總能量守恒律(21).
類似證明可得格式2 所滿足的兩個守恒性質,即:
引理4格式2 在離散意義下保持原問題的兩個守恒性質,即總質量和總能量守恒

3 數值實驗
便于檢驗格式的整體精度,我們引入如下記號

3.1 數值算例1
本例中,我們取ε=α=λ=1,考慮長短波(LS)方程如下

其邊值條件為

初值條件為


上述初邊值問題具有以下精確解

測試空間方向的精度時,我們取時間步長τ = 0.0001,從而可以忽略時間方向的誤差,同樣在測試時間方向精度時,我們取空間步長h = π/100,從而可以忽略空間方向的誤差.在表1 和表2 中,我們分別列出了格式1 在t=1 時,空間與時間方向的誤差數值結果.而在表3 和表4 中,我們則列出了格式2 在t = 1 時,空間與時間方向的誤差數值結果.在表5 中,我們將格式2 與文獻[10]中的格式做了精度比較,圖1 和圖2 我們分別展示了un和vn在不同時間層下精確解和格式1 數值解的變化.

表1: 格式1 在t=1 時刻取不同空間步長時關于空間方向的精度測試

表2: 格式1 在t=1 時刻取不同時間步長時關于時間方向的精度測試

表3: 格式2 在t=1 時刻取不同空間步長時關于空間方向的精度測試

表4: 格式2 在t=1 時刻取不同時間步長時關于時間方向的精度測試

表5: 格式2 與WDFD 格式精度比較

圖1: un 在不同時間層下解的變化:左圖為精確解,右圖為數值解,其中h=π/100, τ =0001

圖2: un 在不同時間層下解的變化:左圖為精確解,右圖為數值解,其中h=π/100, τ =0001
3.2 數值算例2
為了驗證格式1 與格式2 在離散意義下的總能量和總質量守恒律,我們令算例1 中的f =0 和g =0,取計算區域為[0,π]×[0,100],并將數值結果列于圖3 至圖6.

圖3: 格式1 的能量守恒性:左圖為不同時間層總能量,右圖為不同時間層總能量與初始值的誤差

圖4: 格式1 的質量守恒性:左圖為不同時間層總質量,右圖為不同時間層總質量與初始值的誤差

圖5: 格式2 的能量守恒性:左圖為不同時間層總能量,右圖為不同時間層總能量與初始值的誤差

圖6: 格式2 的質量守恒性:左圖為不同時間層總質量,右圖為不同時間層總質量與初始值的誤差
3.3 數值算例3
長短波方程可以描述物理中的孤立波現象,為此,我們添加算例3 用以模擬孤立波的演化,本例中我們考慮如下長短波(LS)方程


實驗中我們采用的是格式1 進行計算,取時間T = 5 時,時間為步長τ = 0.01,空間步長為h=π/10,并將數值結果列于圖7.

圖7: 方程的初始解與T =5 時刻的數值解
從表1 至表4 的數值結果中,清楚地表明本文提出的兩個格式在空間方向和時間方向分別具有四階和二階精度.圖1 和圖2 則顯示數值解與精確解幾乎一致.由表5 則可以看出,格式2 相比WDFD 格式在計算精度上有顯著提高.圖3 至圖6 表明格式1 和格式2 在離散意義下保持原問題的總能量和總質量守恒,這與引理3 和引理4 的結論相符.圖7 模擬了孤立波的演化現象.
4 結論
本文對一類長短波方程組提出了兩個緊致有限差分格式,即格式1 和格式2,兩格式的主要區別在于對非線性項采取了不同的離散方法,但它們均在離散意義下保持總質量和總能量守恒.數值實驗表明,兩個格式在時空分別具有二階和四階精度,具有很好的穩定性而且很好地保持了原問題的兩個守恒性質.同時,數值算例還成功模擬了孤立波的演化過程.

