污染環境中廣義單種群模型的動力學行為分析
曹 明, 王 霞, 唐三一
(陜西師范大學數學與信息科學學院,西安 710119)
1 引言
隨著現代工業和農業技術的迅速發展,大量的有毒物質和污染物被排放到生態環境中,已經嚴重威脅到自然界中物種的生存,導致許許多多的物種滅絕或者處于滅絕的邊緣,甚至影響到人類自身[1].環境污染問題日益嚴峻促使人們去研究環境中有毒物質對物種的影響和評估污染物給物種的生存帶來的風險.因此,污染環境中物種的生存問題的研究變得越來越重要.
早在1980 年,一些學者已經研究了環境毒素對單種群的影響,例如,Hallam 和Clark[2]通過假設種群的增長率是線性依賴于物種吸收毒素的濃度研究了環境中出現的有毒物質對單種群的影響.李冬梅等人[3]研究了一類小容量污染環境中脈沖輸入毒素對具有階段結構的單種群生存問題,分別找到了種群生存與滅絕的閾值.He 和Ma[4]研究了污染環境中的Logistic 單種群模型的生存問題,考慮了生物個體從環境中吸收的毒素濃度和生物個體排泄到環境中的毒素濃度.但是,上述所有的文章中,都忽視了其他外界因素和生物個體將毒素輸入到環境中去的問題.此外,很多文章沒有考慮食物鏈中的毒素對種群的影響問題,為了研究這個問題,Luo 等人[5]提出了污染環境中的單種群模型
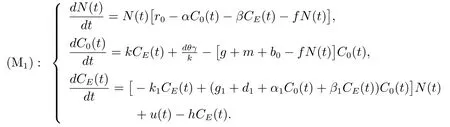
模型(M1)研究了生物體內毒素αC0(t)N(t)、環境毒素βCE(t)N(t)和種內競爭fN2(t)對種群數量的影響.生物體內毒素主要來源于從環境中吸收的毒素(kCE(t))和從食物鏈中吸收的毒素生物體內毒素也可以通過新陳代謝和排泄消除((g + m + b0?fN(t))C0(t)).然而模型(M1)僅考慮了比較特殊的種間競爭關系,不具有一般性,不能較全面的刻畫出種群的動力學行為.為了研究這個問題,本文中,我們將對模型進行改進,提出污染環境中廣義單種群模型,并利用平均積分法深入分析其動力學行為,從而得到更有普遍意義的結果,有利于模型的推廣.
本文中,我們假設環境是一個均勻的完備空間,種群沒有發生遷移并且假設種群中的生物個體間沒有顯著性的差異,建立一個既考慮了環境毒素又考慮了食物鏈毒素對生物個體的影響的更一般的單種群模型,來研究污染環境中毒素對種群生存的影響.在第2 節中,首先給出我們的模型、一些記號、預備知識和重要引理;第3 節中,給出我們的主要結果,即種群一致持久、平均非持久、平均弱持久和滅絕的充分條件,并得到平均弱持久與滅絕之間的閾值條件;第4 節中,通過具體例子來說明我們的主要結論,并利用Matlab 軟件做數值模擬來驗證我們的主要結果;最后,在第5 節中給出了結果討論.
2 模型假設
為了刻畫種群間的不同競爭關系,我們將模型(M1)中的線性競爭函數fN(t)改進成一般函數f(N(t)),從而得到如下更一般地污染環境中廣義單種群模型
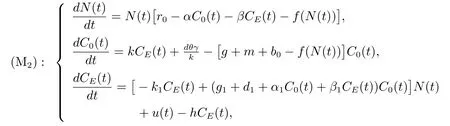
其中r0= b0?d0,表示沒有毒素污染時候種群的內稟增長率,函數u(t)是一個定義在[0,+∞)上的非負連續有界函數,并且此外,我們還定義如下幾個參數的形式[5]:

設模型(M2)初值滿足
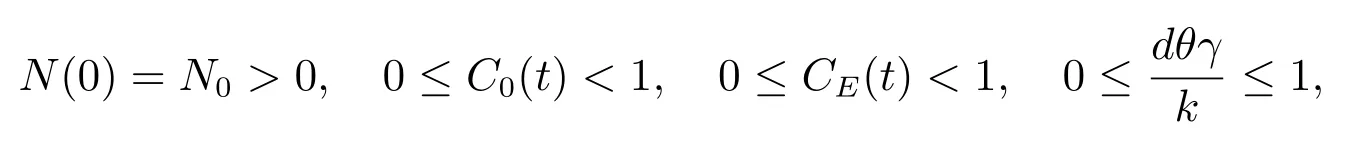
各參數含義如表1 所示.
這里,f(N(t))表示種內競爭關系且滿足如下假設:
(A1): 函數f(N)關于N 滿足局部Lipschitz 條件,關于N 可微,且對于任意N ≥0 函數連續;
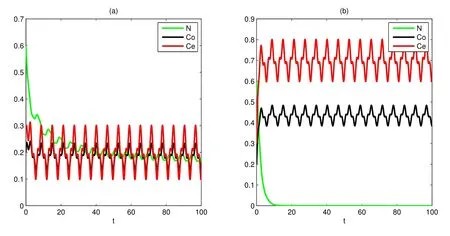
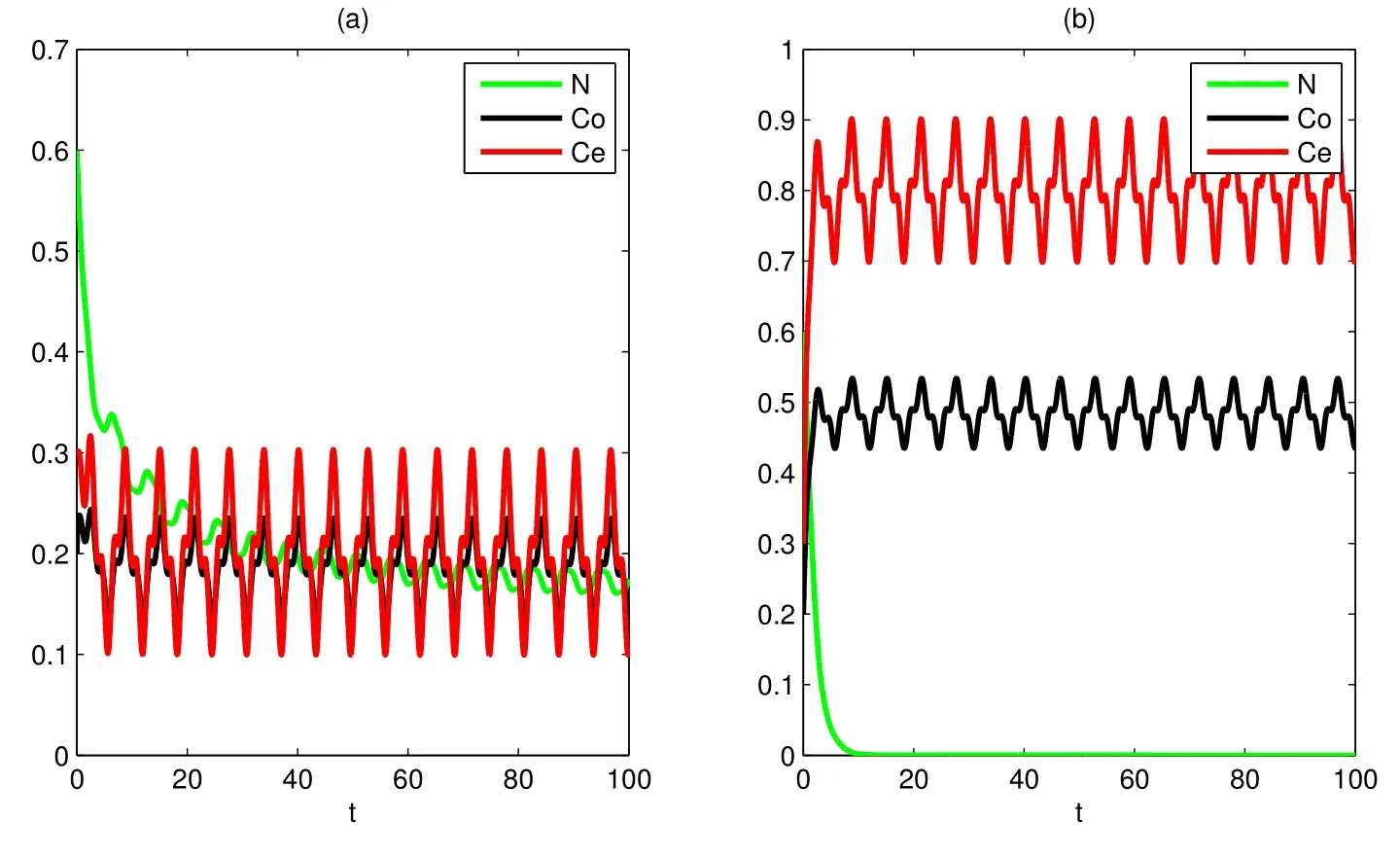
(A3): f(0) 函數f(N(t))更具有一般性,能更全面的反映各種類型的種內競爭關系,因此,模型(M2)更具有一般性,從而能更好地刻畫污染環境中單種群模型的動力學行為. 為了研究方便,首先介紹如下符號表示: R+= [0+ ∞)表示自然數集;表示函數g(t)在區間[0,t]上積分的平均值;表示函數g(t)上確界極限;表示函數g(t)下確界極限;其中g(t)是一個任意函數. 同時給出種群一致持久、平均非持久、平均弱持久和滅絕的定義: 1) 對于任意初值N(0) = N0> 0,若存在常數0 < H1< H2< +∞,使得H1≤N?(t)≤N?(t)≤H2,則稱種群N(t) 是一致持久的; 2) 若?N(t)??=0,則稱種群N(t)是平均非持久的; 3) 若存在正常數K,使得0 在證明我們的主要結論之前,我們先給出幾個重要的引理: 引理1對于模型(M2),集合 是一個不變集.若假設條件(A1)、(A2)和(A3)都滿足,則方程(M2)的任意解N(t)都是有界的. 證明 因為N(t) = 0 是模型(M2)中第一個方程的解,所以對于任意初值N(0) >0,都有N(t)>0, t ∈R+,很顯然有 模型(M2)的解軌線在相空間中不能穿過任何坐標平面,所以 是一個不變集. 從假設(A2),我們知道f(N)是一個增函數,因此存在一個正常數c1,使得f(c1) >r0.令c2= max{x0,c1},如果對于N(t)中所有t 的存在區間,都有不等式N(t) < c2成立,則結論明顯成立.現在假設N(t2) > c2僅對N(t)中t 的存在區間中的某些值成立,根據假設(A1),必定存在一個t1且0 ≤ t1< t2,則有N(t1) = c2.所以對于任意t ∈[t1,t2],我們得到N(t)≥c2,根據模型(M2)中第一個方程,有 這個矛盾意味著N(t) ≤ max{x0,c1}.因此,N(t)在定義區間上是有界的,所以N(t)是定義在R+上的. 其中ε<δ 由于ε 的任意性,f(N)是連續函數,上述不等式意味著當t ∈R+時,有 由模型(M2)中第一個方程,可得 考慮如下方程 由于模型(M2)中第一個方程有一個正穩定平衡點因而對于任意ε > 0,當t ∈R+時,有 根據比較定理可知 根據引理1,我們知道對于模型(M2),從任意正初值出發的解都是正的.下面給出C0(t)和CE(t)的有界性. 引理2對于模型(M2),若g+d0+α+β 引理2 的證明參見文獻[5]中引理2.2 的證明. 在本節內容中,我們將討論種群模型(M2)的一致持久、平均非持久、平均弱持久和走向滅絕的條件.我們假設文章第三部分所有定理都滿足引理2 的條件.由于模型(M2)的最后兩個方程是非線性的,難以用u(t)將C0(t)和CE(t)表示出來,在這種情況下,我們通過平均積分方法來分析模型(M2)的動力學行為,模型動力學行為的條件僅受到模型參數或者已知函數u(t)的影響. 接下來的定理1,我們將證明得到種群N(t)一致持久的充分條件. 定理1對于模型(M2),若假設條件(A1)、(A2)、(A3)和 同時滿足,則種群N(t)從任意初值N0> 0 出發都將一致持久.其中f(0)表示在初值N0處的任意種內競爭關系. 證明 通過引理1,我們知道對于任意t ∈R+,有和 0 ≤ CE(t) ≤1.因此,對于任意ε1> 0,存在t1> 0,使得當t > t1時,有成立.從模型(M2)的第二個方程我們知道 由于方程 有一個穩定的平衡點 因而,對于任意的ε2>0,存在常數t2>t1,使得當t2>t1時,有 從(3)式和(4)式,我們知道 因此,可知 根據定理假設條件,我們可以選擇充分小的ε1和ε2,使得 其中θ 是一個正常數,由(5)和(6)式,可得 考慮方程 顯然方程(8)是一個Logistic 方程,其解析解為 由(9)可知 故根據標準比較定理可知 所以有 根據引理1 可知種群將會一致持久,定理證畢. 說明1定理1 說明了當種群內稟增長率r0較大時,種群是很容易持續存活下去的,生物體本身對毒素的排泄和凈化能力比較強也是有益于種群的持續生存的.但是,種群對環境毒素的吸收率k 較大,對體內毒素反應系數α 和對環境毒素反應系數β 較大時都不利于種群的持續生存,這是符合實際的. 研究種群N(t)平均非持久的充分條件,我們將會得到如下定理. 定理2對于模型(M2),若假設條件(A1)、(A2)、(A3)和r0= f(0)同時滿足,則種群N(t)從任意初值N0>0 出發都將會平均非持久,即?N(t)??=0. 證明 因為當t ∈R+時,N(t) > 0,所以N(t)在閉區間[0,t]上的積分是正值,即因此,存在充分小的ε>0,使得 (10)式兩邊同時除以t 并取上極限,得到 因為r0=f(0),可知道?N(t)??≤0.根據夾逼準則可得?N(t)??=0.定理證畢. 種群的持久與滅絕情況是我們最關心的問題,我們將在接下來的定理3 中證明得到種群平均弱持久與滅絕之間的閾值條件以及種群平均弱持久的充分條件和種群走向滅絕的充分條件. 定理3對于模型(M2),滿足假設條件(A1)、(A2)、(A3),并令 (i) 若 則: (a) 當 時,種群N(t)將平均弱持久; (b) 當 時,種群N(t)將會滅絕. (ii) 若 則: (a) 當 時,種群N(t)將平均弱持久; (b) 當 時,種群N(t)將走向滅絕.其中f(0)表示在初值N0處的任意種內競爭關系. 證明 對模型(M2),將每個方程從0 到t 進行積分,然后在等式兩端同時除以t,可得到 由方程(12)引出 將等式(14)代入等式(11),可得 模型(M2)的第一個方程可以引出 因此可得 結合等式(13)–(16),可得 若?N(t)??= 0,即和?N(t)??= 0,將得出矛盾.因為N(t)是非負有界的,0 ≤C0(t)≤1, 0 ≤CE(t)≤1,由(15)式,我們得到 這與(i)中的條件(a)及(ii)中的條件(a)矛盾. 接下來,我們將證明(i)中的條件(b)及(ii)中的條件(b).若(i)中的條件(b)和(ii)中的條件(b)的結論不成立,即?N(t)??> 0 時,我們將證明它與(i)中的條件(b)和(ii)中的條件(b)是相互矛盾的. 因為對于任意t>0,有0 ≤C0(t)≤1, 0 ≤CE(t)≤1,由(13)式,我們有 現在我們有 若?N(t)??≥ 0,則我們知道 ?u(t)??≤ ?G(N)??.根據引理1 我們知道N(t) ≤所以很容易看出G(N)在區間上取得大值的點必然在區間的端點處,即 這與(i)中的條件(b)矛盾.若 則與(ii)中的條件(b)矛盾.定理證畢. 說明2定理3 說明了當外部毒素輸入量?u(t)?最低極限水平低于 值時,種群是平均弱持續的.若生物體對環境毒素的吸收能力k 值減小,體內毒素反應系數α 和環境毒素反應系數β 減小,而生物體內毒素的排泄率g 和生物體自身對毒素的凈化率m 的都增大,且種群內稟增長率r0與環境的自我凈化能力h 增大,則生物種群抵抗污染的能力更強.但是過量對環境輸入毒素必定會使種群走向滅絕. 在模型(M2)中,若令f(N(t)) = fNσ(t),其中σ 是個正常數且σ1,我們得到如下模型 顯然,當σ =1 時,模型(M3)就是模型(M1),所以模型(M1)是模型(M2)的特殊情況. 若N > 0,易知函數f(N) = fNσ滿足假設(A1)、(A2)和(A3).根據引理2,我們得到如下推論: 推論1對于模型(M3),若 則任意從初始條件N0> 0 出發的解(N(t),C0(t),CE(t)),對所有t ∈ R+,有N?(t) ≤成立,且 0 ≤ C0(0) ≤ 1 和 0 ≤ C0≤ 1 也成立. 推論1 的證明參見文獻[6]中推論1.1 的證明. 若f(N)=fNσ時,有f(0)=0,根據定理1 很容易得到如下推論: 推論2若 則對于模型(M3)的解N(t)從任意初值N0>0 出發,種群都將一致持久. 當f(N(t))=fNσ(t)和f(0)=0 時,根據定理3 可得到如下推論: 推論3假設模型(M3)滿足條件(A1)、(A2)、(A3),令 (i) 若 則: (a) 當 時,種群N(t)將會平均弱持久; (b) 當 時,種群將走向滅絕N(t). (ii) 若 則: (a) 當 時,種群N(t)將會平均弱持久; (b) 當 時,種群N(t)將走向滅絕. 接下來我們利用數值模擬來說明我的實例,考慮模型(M3),當α = 1, β = 0.5, f =0.5, σ = 2, k = 4, d = 4.5, θ = 1, γ = 0.6, g +m+b0= 8, k1= 0.004, α1=0.001, β1= 0.004, h = 1, u(t) = 0.1 sin(t) + 0.1 cos(3t) + δ(δ ∈ R+)時,令r0=2.5, g1+d1=0.001, δ =0.5 模型(M3)滿足推論1 的條件.我們給模型(M3)設置初始值 模型(M3)的解如圖1(a)和圖1(b)所示,種群N(t)從初值N0>0 出發將一致持久. 令r0= 0.3, g1+d1= 0.001,當δ = 0.2 時,模型 (M3)滿足推論 3 中(i)(a)的條件,模型(M3)從初始值(N0(0),C0(0),CE(0)) = (0.6,0.2,0.3)出發,其解如圖2(a)所示,很顯然種群N(t)從初值N0> 0 出發將平均弱持久;當δ = 0.7,模型(M3)滿足推論3 中(i)(b)的條件,模型(M3)從初始值(N0(0),C0(0),CE(0))=(0.6,0.2,0.3)出發,其解如圖2(b)所示,種群N(t)從初值N0>0 出發將走向滅絕. 圖1: 當r0 =2.5,初始值為(0.6,0.2,0.3)和(2.6,0.5,0.7)時,模型(M3)的動力學行為 圖2: 推論3 中條件(i)成立時,模型(M3)的動力學行為 令r0=0.3, g1+d1=0.04,當δ =0.2 時,模型(M3)滿足推論3 中(ii)(a)的條件,模型(M3)從初始值(N0(0),C0(0),CE(0)) = (0.6,0.2,0.3)出發,其解如圖3(a)所示,很顯然種群N(t)從初值N0> 0 出發將平均弱持久;當δ = 0.8 時,模型(M3)滿足推論3 中(ii)(b)的條件,模型(M3)從初始值(N0(0),C0(0),CE(0)) = (0.6,0.2,0.3)出發,其解如圖3(b)所示,種群N(t)從初值N0>0 出發將走向滅絕. 圖3: 推論3 中條件(ii)成立時,模型(M3)的動力學行為 污染環境中的單種群模型在以往文獻中已有很多研究,本文中在以往模型的基礎上對模型進行推廣提出了污染環境中的廣義單種群模型(M2),不僅同時考慮環境毒素和食物鏈毒素對種群的影響,而且用一般函數來刻畫種群間的競爭關系,從而考慮多種不同競爭關系下環境污染對種群生存的影響.通過研究我們得到了污染環境中單種群模型一致持久、平均非持久、平均弱持久和滅絕的充分條件,并且還得到平均弱持久與滅絕之間的閾值條件.與已有的模型相比較,我們的模型(M2)不僅考慮了環境毒素對種群的影響,還考慮了食物鏈毒素對種群的影響,特別是我們將種間相互作用關系函數fN(t)改進成f(N(t))的形式,使得我們的模型與已有的模型相比而言更具有一般性.因此,與前人的研究成果相比,本文的結論更具有一般性.改進后的模型(M2)有利于我們將模型進行推廣應用,對于各種不同的生物種群,刻畫它們之間的種間競爭關系的函數也是不同的,但是不論對于什么樣類型的生物種群,它們之間的復雜的種間關系都能夠在我們改進的模型模型(M2)中通過一般函數f(N(t))反映出來,就可以用本文的結論來研究不同生物種群的動力學行為.







3 主要結果
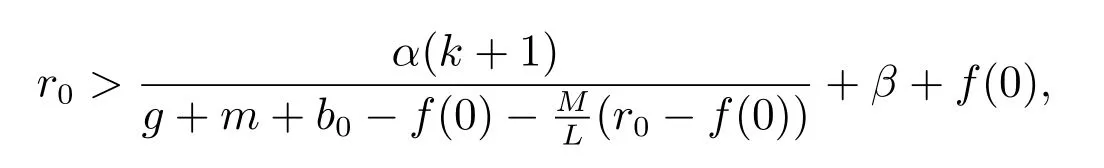



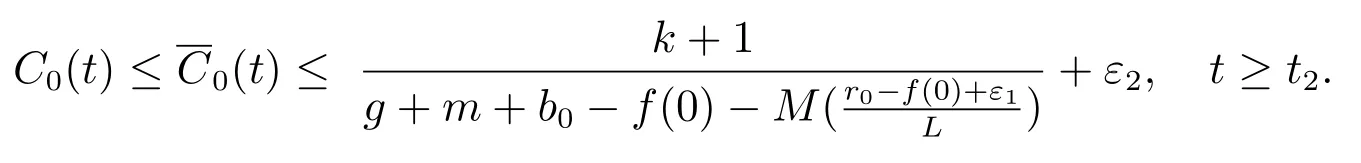
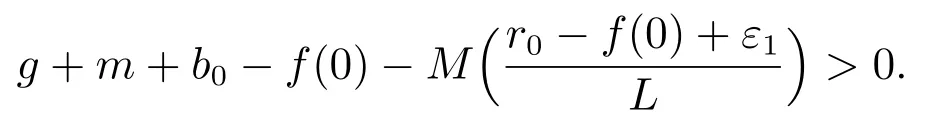

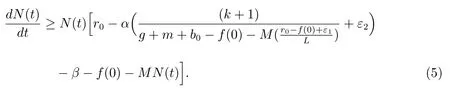





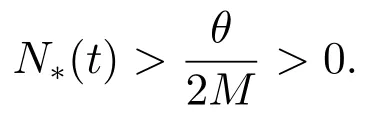

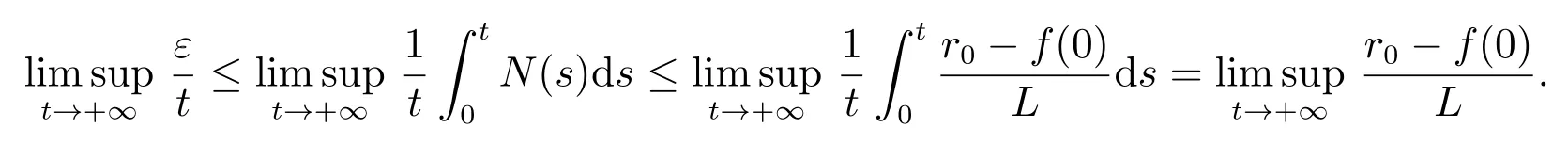








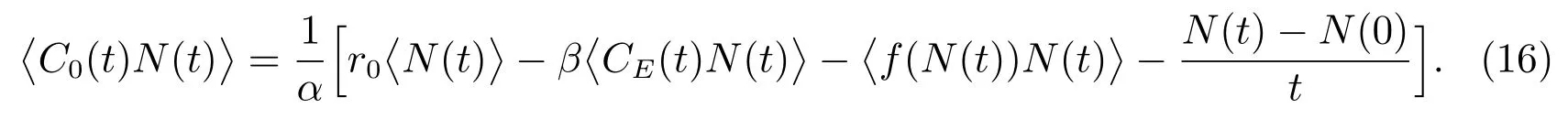







4 實例分析
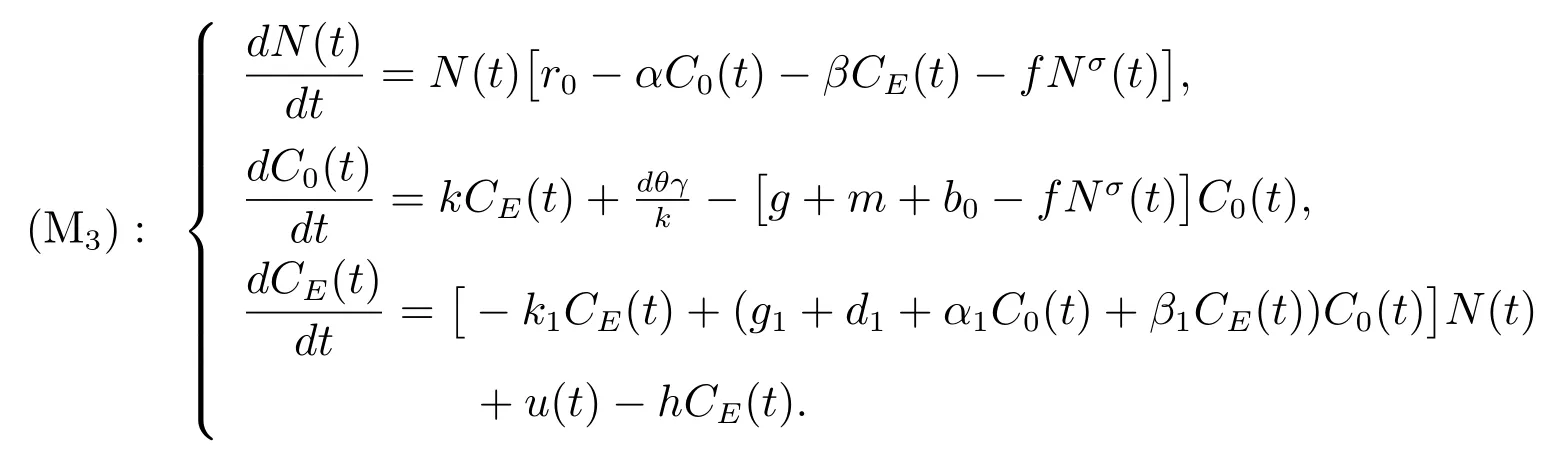
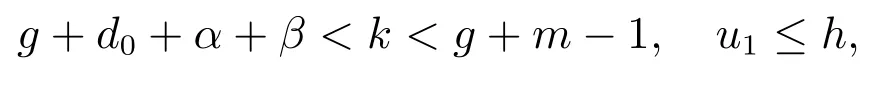

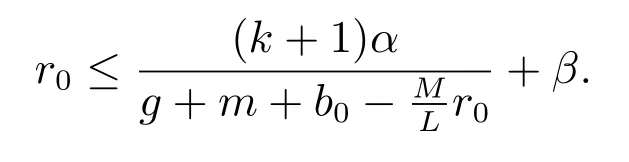

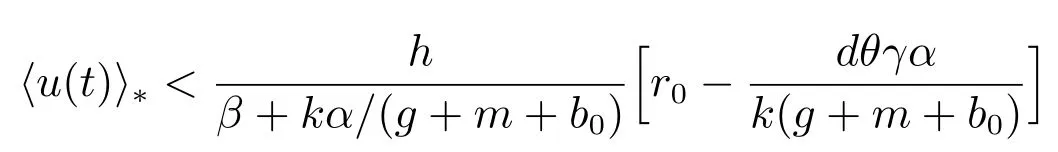
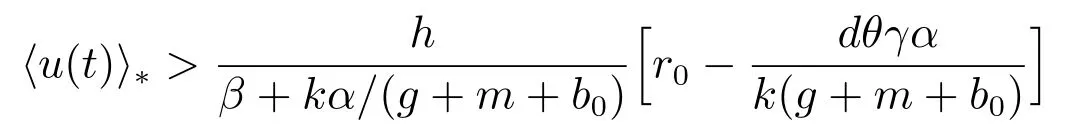
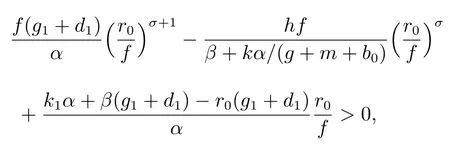

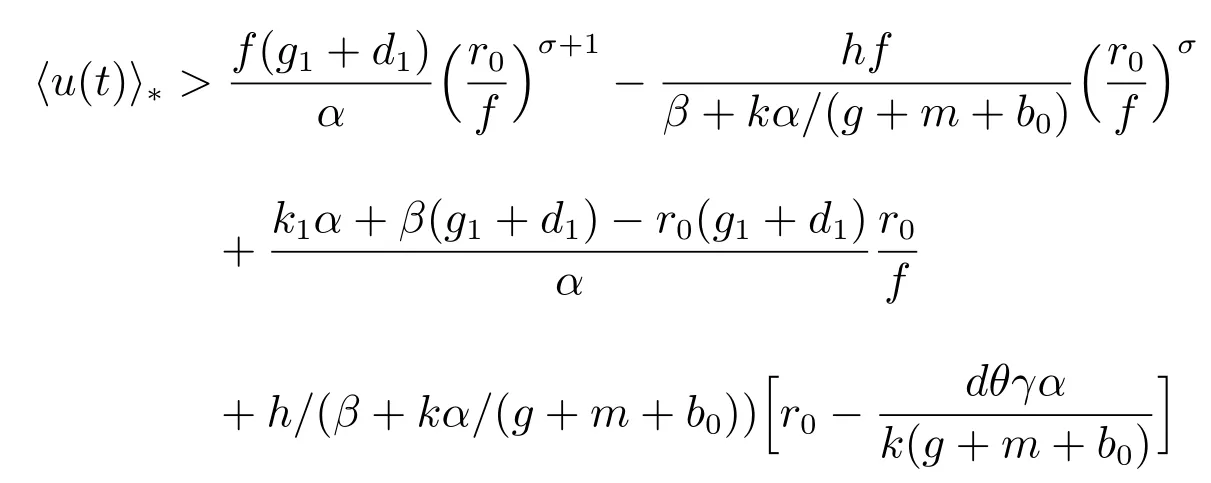


5 討論

