基于概率統計的BK7玻璃磨削亞表層損傷深度在線預測技術
呂東喜,陳明達,姚友強,趙 岳,祝穎丹,2*
(1. 中國科學院 寧波材料技術與工程研究所 浙江省機器人與智能制造裝備技術重點實驗室,浙江 寧波 315201;2. 中國科學院大學 材料與光電研究中心,北京 100049)
1 引 言
硬脆材料的磨粒加工過程通過宏/微觀裂紋的成核及擴展,在去除材料的同時不可避免地引起工件的亞表層損傷(Subsurface Damage Depth,SSD)[1-2]。鑒于亞表層裂紋對硬脆材料工件機械和光學性能的負面影響,需要在后續加工過程中通過優化工藝參數逐步降低工件的亞表層裂紋深度,其前提是對工件SSD深度的準確、快速預測,以縮短后續加工時間,提高加工效率。
為了快速準確地預測工件的SSD深度,人們提出了大量基于磨粒粒度[3-4]及工件表面粗糙度[5-7]的亞表層裂紋擴展深度預測方法,極大地方便了光學零件的加工。然而,基于磨粒粒度的預測技術精度十分有限,預測結果甚至相差數倍,難以實現對裂紋深度的精確評估[8]。為了提高預測精度,人們提出了基于表面粗糙度的SSD深度預測方法。Li等人[6]基于壓痕斷裂力學理論,綜合考慮彈/塑應力場對中位裂紋擴展的促進作用,建立了表面粗糙度與亞表面裂紋深度之間的非線性關系模型,實現了對工件SSD深度的預測。LV等人[7]分析了磨粒壓痕過程中側向裂紋成核深度和中位裂紋擴展長度之間的內在關聯,建立了基于工件表面粗糙度(p-v值)的快速、準確、無損預測亞表層裂紋深度的理論模型。
雖然基于表面粗糙度的SSD深度預測技術精度較高,但是該類方法并不能對工件的亞表層裂紋深度進行在線預測。為此,Wang等人[9]分析了單磨粒壓痕力與中位裂紋深度的內在關聯,結合對刀具端面磨粒數目的統計分析,建立了刀具切削力與亞表層裂紋深度之間的非線性關系模型,實現了對旋轉超聲加工過程中SSD深度的在線預測。該理論模型假設刀具端面上的磨粒具有相同的高度,且均參與亞表層裂紋的形成。然而實際參與切削的磨粒僅占刀具端面磨粒數目的很少一部分[10],并且參與切削的磨粒尺寸明顯不同,導致單個磨粒的切削深度存在較大差異,并最終影響亞表層裂紋的擴展深度。
本文首先基于硬脆材料的壓痕斷裂力學理論,研究單個磨粒壓痕深度與中位裂紋擴展長度之間的內在關聯;隨后利用概率統計法對刀具端面邊緣的磨粒數目進行分析,建立了刀具切削力與單個磨粒切削深度之間的理論關系模型;在此基礎上,提出了快速、準確、在線預測工件SSD深度的方法,并結合BK7玻璃的磨削實驗進行了驗證。
2 單磨粒壓痕深度與中位裂紋擴展長度的映射關系
從材料去除機理角度而言,硬脆材料的磨削加工過程可以簡化為大量尖銳壓頭對工件加工面的隨機性印壓過程[11]。因此可以借助于壓痕斷裂力學理論,研究實際磨削加工過程中亞表層裂紋的形成機理,如1(a)所示。在磨粒-工件的相互擠壓作用下,材料內部會形成復雜的彈/塑性應力場,并產生兩種基本的裂紋構型[12]。側向裂紋成核于塑性變形區域的底部,并沿平行于加工面的方向橫向擴展,當延伸至工件的自由面時,實現材料的脆性斷裂去除。 而中位裂紋同樣成核于塑性變形區域底部,并沿垂直于加工面方向向下擴展,最終形成工件的亞表層損傷(見圖1(a))。
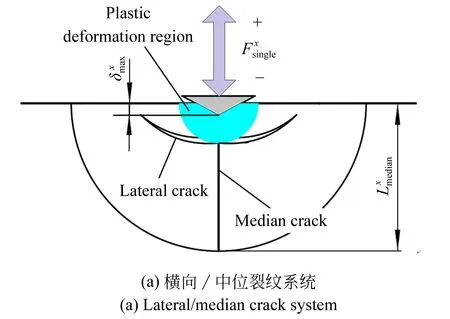

圖1 單磨粒印壓作用誘發的裂紋系統


(1)
其中HV為材料的維氏硬度。

(2)
其中:q=0.5,為無量綱常數;αk=0.027+0.090×(q-1/3);E和KIC分別為材料的彈性模量和斷裂韌性。

(3)
3 刀具端面邊緣磨粒數目的統計分析
3.1 刀具端面邊緣的磨粒數目
現有的SSD深度預測方法假設刀具端面上所有的磨粒均參與材料去除[6],然而對刀具磨損形貌的顯微觀察表明,只有端面邊緣的磨粒參與了材料去除[15]。磨削加工過程及刀具端面上磨粒的分布特征如圖2所示。
為了準確獲得參與切削的磨粒數目,LV等人分析了磨粒的平均間距b與其進給量之間的關系,并指出只有距離端面邊緣小于b范圍內的磨粒才有可能參與實際加工[7],并推導出端面邊緣磨粒數目Nall的計算公式:
(4)

需要特別指出的是,在實際磨削加工過程中,參加切削的磨粒數目不僅取決于磨粒的尺寸,還與刀具的切削深度密切相關,即有效磨粒數目僅為刀具端面邊緣磨粒數目Nall的一部分。
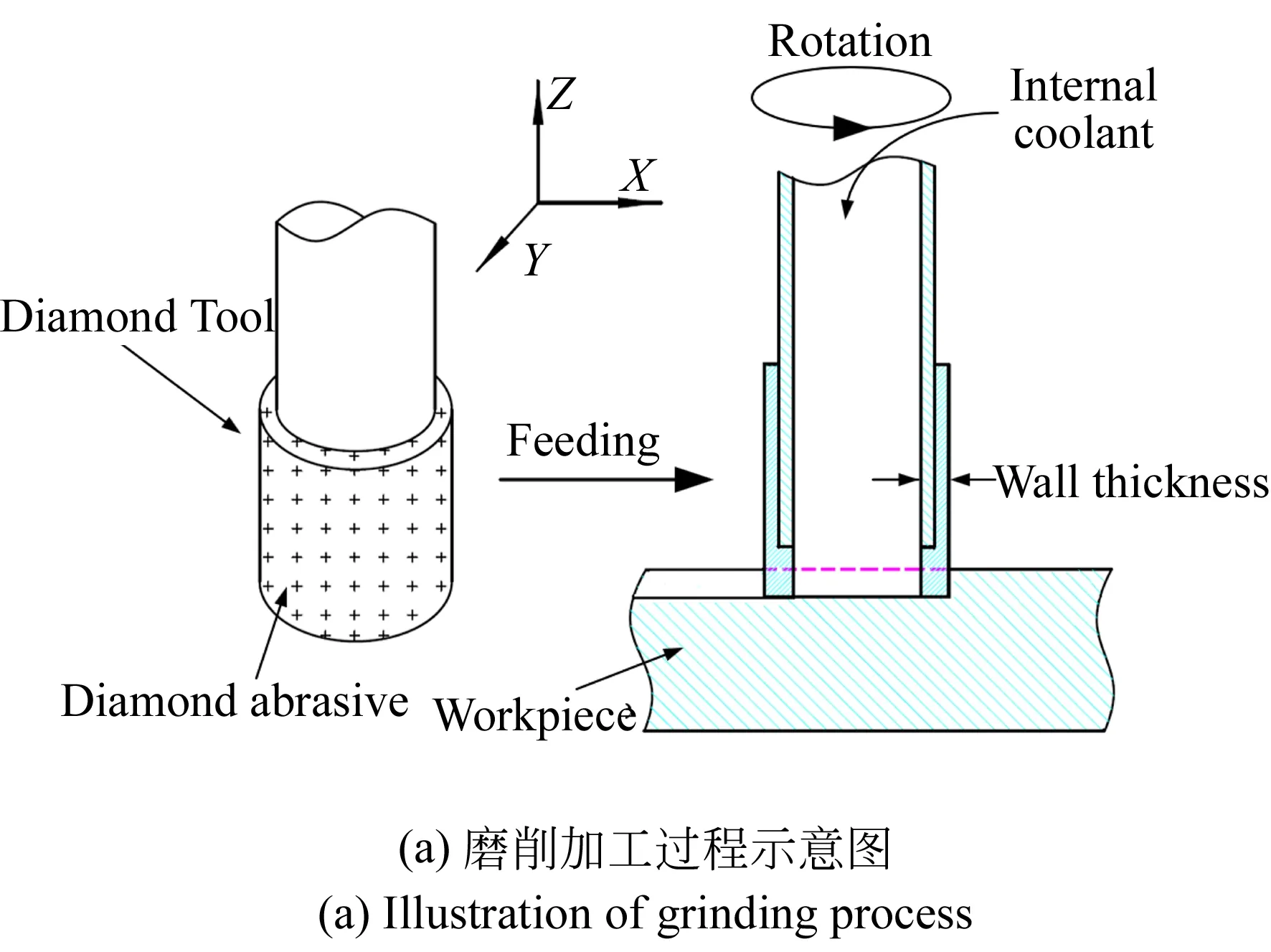
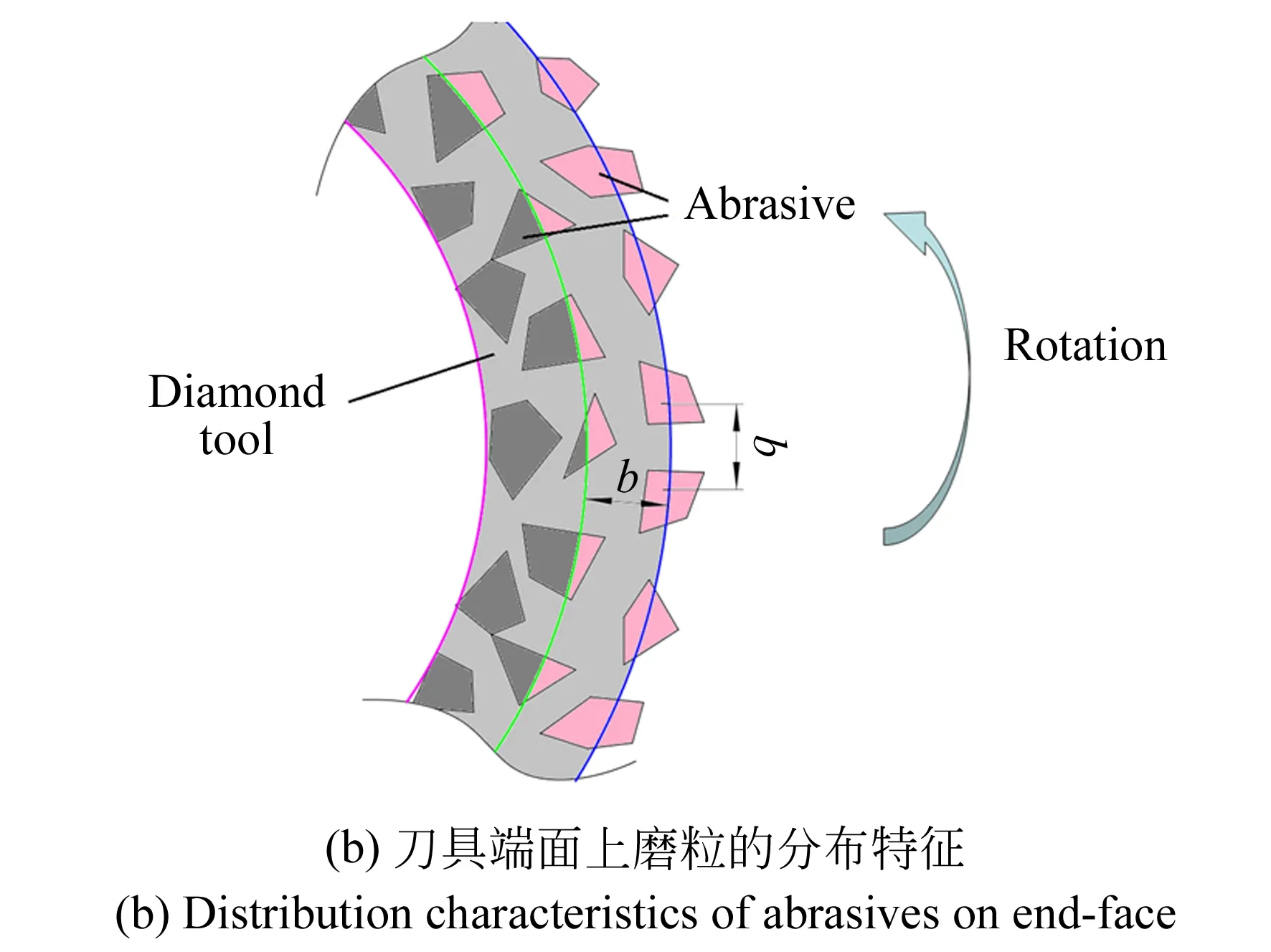
圖2 磨削加工過程示意圖及磨粒分布
3.2 磨粒高度的高斯分布特征
Hou等人借助于光學顯微鏡對刀具表面磨粒的高度dx進行了統計分析,發現最大高度為dmax和最小高度為dmin磨粒的數目都非常少,而平均高度的磨粒最多,并且磨粒高度在一定范圍內服從高斯分布[10](見圖3),其分布函數為:
(5)
式中:x為隨機變量;y為隨機變量x的方差。

圖3 磨粒高度的高斯分布特征
顯然,磨粒高度的概率方程P(p)為圖3中綠色區域的面積(彩圖見期刊電子版),其值可以通過對式(5)從p到+進行積分獲得:
(6)
4 SSD深度預測模型的建立
4.1 刀具切削力和磨粒切削深度的內在關聯
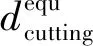
(7)
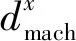
(8)


(9)
式中:Δ為最大磨粒高度dmax與最小磨粒高度dmin的差值,即Δ=dmax-dmin。
(10)
(11)
在這種情況下,所有參與切削的磨粒的合力可以近似認為是刀具的切削力F,其值可通過對式(11)進行積分獲得:
(12)
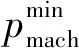

(13)
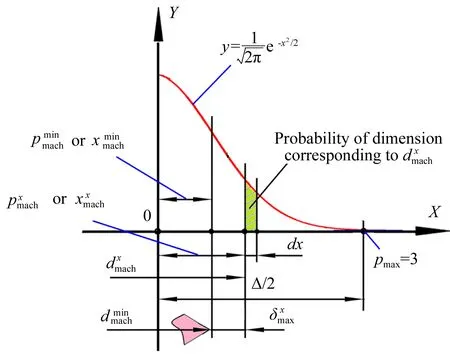
圖4 高度為磨粒的分布概率
將式(1)和式(4)帶入式(12),可得刀具的切削力F與單個磨粒切削深度δx的理論關系模型:
(14)
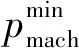
(15)
將式(15)帶入式(14)可得刀具的切削力為:
(16)


4.2 基于刀具切削力的SSD深度在線預測方法

(17)
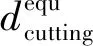
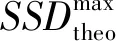
(18)
其中:ξ為比例系數,j為定值。ξ和j可以通過擬合一系列的實驗數據獲得,其值與工藝參數無關。因此,在已經ξ和j的基礎上,結合式(16)~式(18)可以實現對實際磨削加工過程中工件亞表層裂紋深度的在線預測。需要特別指出的是,本研究假設脆性斷裂為唯一的材料去除方式,因此上述方法并不適用于預測材料在延性和半延性去除過程中引起的SSD深度。
5 實 驗
5.1 實驗條件
Wang等人使用金剛石刀具在德國德瑪吉公司生產的Sauer Ultrasonic 50 數控加工中心上進行了普通磨削加工實驗,詳細的實驗參數如表1所示[9]。實驗過程中,采用瑞士Kistler公司的9256C2型測力儀對磨削過程中的切削力進行了檢測。

表1 磨削實驗的加工參數[9]
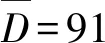

表2 BK7玻璃的材料屬性[9]
5.2 實驗結果與分析

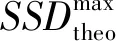

圖和SSDmax之間的關系曲線
6 結 論


