一招割補法 制勝求面積
姚娟妹
數學世界浩瀚如海,代數幾何變幻無窮。平面直角坐標系中求不規則圖形的面積問題時常出現。求不規則圖形的面積沒有公式可直接運用,看似不可能解決,但是如果能把它變成可以計算出面積的規則圖形,那么問題就迎刃而解。我們以平面直角坐標系中求三角形的面積為例,領略其中的奧妙。
一、直接利用三角形面積公式
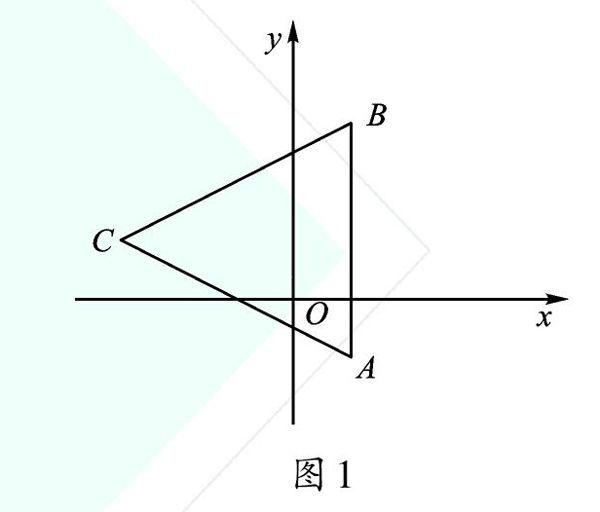
例1 如圖1,已知A(1,-1),B(1,3),C(-3,1),求△ABC的面積。
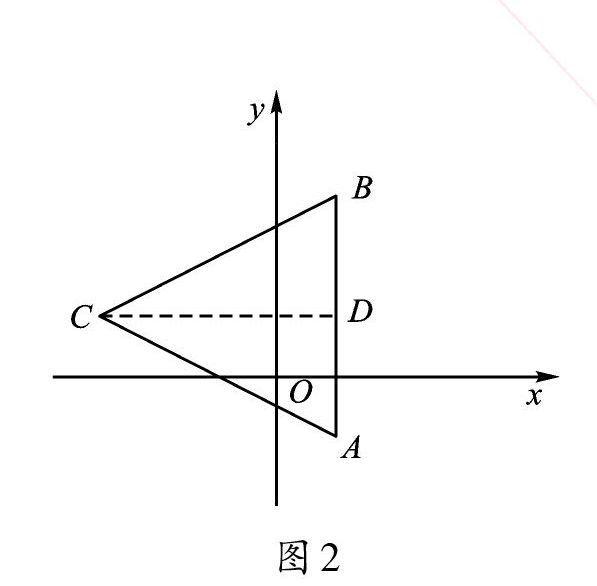
【點撥】如圖2,該三角形有一條邊AB∥y軸,AB的長度等于A、B兩點的縱坐標差的絕對值,AB邊上的高CD等于C、D兩點的橫坐標差的絕對值,再將AB、CD的長度代入三角形面積公式即可。當三角形有一邊平行于坐標軸時,通常以這條平行于坐標軸的邊作為三角形的底邊,易于求解。
【解析】如圖2,過點C作CD⊥AB于D,AB=4,CD=4,S△ABC=1/2×AB×CD=1/2×4×4=8。
二、化“不規則”為“規則”
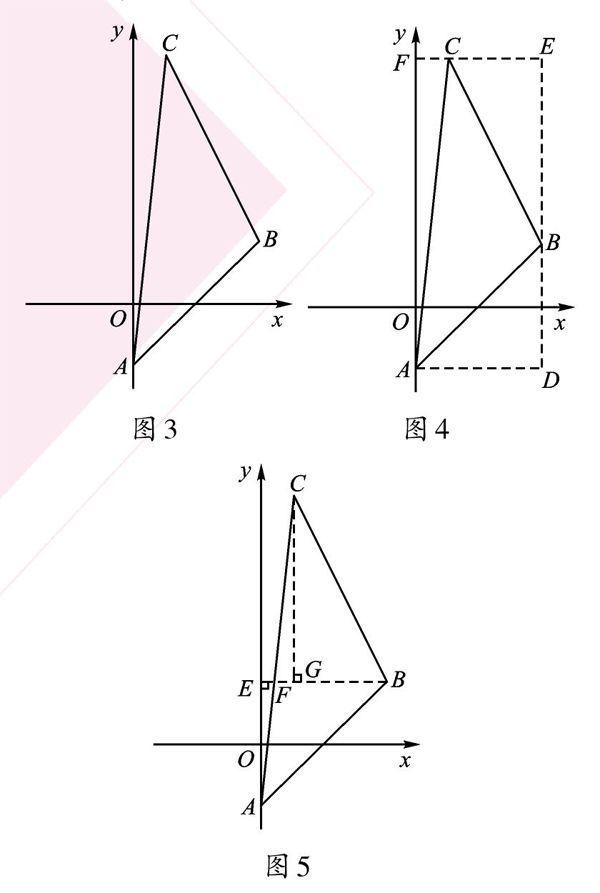
例2 如圖3,在平面直角坐標系中,已知A(0,-2),B(4,2),C(1,8),求△ABC的面積。
【點撥一】初看此題,△ABC為“不規則”圖形,感覺無從下筆。仔細看圖就會發現,我們只要過三角形的頂點作x軸或y軸的平行線,把三角形補成一個矩形,再用該矩形的面積減去其他3個“規則”三角形的面積,即可求解。這種方法我們稱為“補形”。
【方法一】如圖4,分別過A、C作x軸的平行線,過B作y軸的平行線,得到矩形ADEF,S△ABC=S矩形ADEF-S△ABD-S△BCE-S△ACF=18。
【點撥二】當三角形的三邊都不平行于坐標軸時,可以過三角形的某一頂點作z軸或者y軸的平行線,將三角形分割成兩個三角形,再分別求這兩個三角形的面積。這種方法稱為“分割”。
【方法二】(有興趣的同學可嘗試)如圖5,過B作BE∥x軸,交y軸于點E,交AC于點F;過C作CG_LBE于點G。CG=8-2=6,AE=2-(-2)=4。由A(0,-2),C(1,8),可以求得直線AC的解析式為y=10x-2,又由BE∥x軸,可得F點坐標為(2/5,2),所以BF=4-2/5=18/5,故:S△ABC=S△ABF+S△BCF=1/2×BF×AE+1/2×BF×CG=18。
2
求平面直角坐標系中三角形面積一般先確定三角形的頂點坐標,找準三角形的底和高。也可以將三角形補成一個規則圖形,如矩形。或者將三角形分割成兩個三角形,然后再求解。上述題目除了用割補法求解,還可以考慮用等積變換等方法來解,有興趣的同學可以嘗試一下。

