水中航行器控制分配技術應用現狀

李岳明，王小平，張英浩，龐家明，閆力新

(哈爾濱工程大學船舶工程學院 水下機器人技術重點實驗室，黑龍江 哈爾濱 150001)

0 引 言

近年來，過驅動航行器越來越流行，例如飛行器F-22戰機，水下航行器X舵潛艇，陸地上的獨立四輪驅動汽車。過驅動航行器采用多操縱面布局，相比于傳統布局，能提供多種操縱面組合方式進行運動控制，極大提高了機動性、操縱性、容錯性。增加操縱面的同時也帶來復雜的控制分配問題，控制分配相關研究始于20世紀90年代，經過幾十年的研究發展，飛行器控制分配技術已經比較成熟，常見的控制分配方法有廣義偽逆法、加權偽逆分配法、直接分配法、鏈式分配法、數學規劃法等[1-3]，以及考慮動態約束的動態分配[4-5]。

相比飛行器，水中航行器（包括特種船舶、海洋平臺、智能水下機器人等）在控制分配技術的研究還不夠深入。將來人們必將對水中航行器的操縱性提出更高的要求，X-舵潛艇是一種具有代表性的過驅動水中航行器，德國212A型潛艇，荷蘭“海象”級潛艇都采用了X-舵，X-舵擁有比十字舵更小的回轉半徑等優點。現代船舶設計中，船舶通過裝備多個推進器、舵、減搖鰭等執行機構來提高操縱性，981海洋鉆井平臺就配備8臺全方位推進器[6]。除船舶外，許多ROV和AUV也涉及過驅動控制分配[7]，沈陽自動化研究所研制了一型X-舵AUV[8]，但是采用對角聯動的控制方式，是獨立四舵X舵的一種特殊操縱組合方式。關于AUV的控制分配技術研究并不多見，特別是在基于舵的控制分配技術方面。已經成功應用于水中航行器的控制分配方法有偽逆法、偽逆再分配法[9]、最優化分配法[10]、不動點迭代[11]、數學規劃法[12]等。本文重點分析水中航行器的控制分配技術應用研究現狀，并對將來的發展方向做一個展望。

1 過驅動航行器

過驅動系統是一類控制輸入數（執行機構數量）多于輸出數（期望產生力矩數）的系統，其基本思想是采用多組執行機構實現近似的控制效果，并通過控制分配將控制指令合理、有效地分配到各個執行器上。過驅動系統不僅可以提高航行器的機動性，可靠性，并且具備靈活的操控組合方式，能提高系統容錯性。具有代表性的過驅動航行器對象如圖1所示，采用X舵的AUV，擁有4個獨立的舵葉。圖2為采用X舵的德國212A型潛艇，圖3為上海交通大學研制的配備8臺推進器的深海作業型ROV，圖4為法國ECA公司的Alistar 3000型AUV。

圖1 X-舵AUVFig. 1 X-rudder AUV

圖2 德國212A型潛艇Fig. 2 German 212A submarine

2 控制分配問題描述

對于虛擬控制指令v(t)∈Rn，操縱面輸入為u(t)∈Rm。實際輸入與期望控制力矩的映射可以表示為f：。操縱面與期望力矩之間的線性關系可以表示為：

圖3 上海交通大學4 500米級ROV“海馬”號Fig. 3 Shanghai Jiaotong University 4 500 m ROV Haima

圖4 法國ECA Alistar 3 000 AUVFig. 4 The ECA Alistar 3000 AUV of France

約束條件式中：B為控制效率陣；u為 所有執行機構組成的操縱向量；v為期望操縱力矩，在水下機器人中，由俯仰力矩、偏航力矩和滾轉力矩組成；和分別為所有執行機構約束向量。

非線性的分配關系可表示為：

3 水上航行器推力控制分配

文獻[13]論述對于船舶運動控制，通常安裝多個可以實時改變推力和轉矩的執行機構，包括螺旋槳、舵、鰭等裝置，由它們共同產生控制器計算得到系統所需要的力和力矩，而控制分配技術是關鍵。

3.1 基于增加約束的控制分配法

在船舶增加了各種操縱機構后，控制分配的組合方式也變得多樣化，這給求解問題帶來一定難度。基于約束的控制分配是其中簡單有效的控制分配方法。增加約束后，求解未知數的個數等于方程個數，將多解問題變為一個求解線性方程組唯一解的問題，使計算簡單方便，但解的精度可能不高，也不一定是最優解。增加約束條件主要靠經驗，但同時也要根據實際目的，遵守簡單實用的原則。文獻[14]將此方法用于控制分配，分配模型如下：

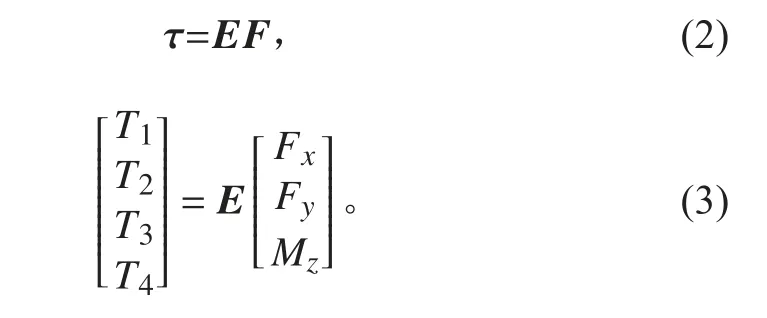
式中：τ為所需推力（矩）；E為推進器配置矩陣；F 為各個推進器產生的力（矩）矩陣。由于求得τ有4個未知量，但是只有3個等式，因此會有無窮解，甘永在其論文中提出了增加約束的一種控制分配方法，例如增加

文獻[15]也將此方法用于水下機器人的控制分配。

3.2 偽逆法

控制分配技術中應用最廣，最具代表性的當屬偽逆控制分配，許多的控制分配方法都是以偽逆控制分配為基礎進行開發。偽逆法[16]具有計算量小和易于實現等優點，但沒有考慮操縱面的飽和（位置和偏轉速率）約束限制，也不能實現可達集的全覆蓋。Bordignon等[17]通過F-18HARV實驗得出偽逆法只可實現可達集中的部分虛擬指令，最好的情況也只能達到其中的42.7%。

這里所介紹的偽逆是Moore-Penrose逆矩陣，可以通過證明矩陣的偽逆是唯一的[18]，欠定方程組的偽逆解是方程組的一個可行解，如下：Bu

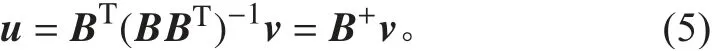
式中： 為 的偽逆矩陣，為一個可行解。基于偽逆法控制分配方法還有偽逆加權分配法。

3.3 鏈式分配法

Roger Skjetn等[9]提出了基于偽逆法的通用遞歸算法用于控制分配，并且為期望產生的各方向力矩設定優先級，這樣做的好處是：遞歸設計將確保首先在最高優先級控制方向上使用可用控制容量，然后在次要方向上使用剩余容量，依此類推。換句話說，避免在無法實現可行性的情況下違反τ的所有方向，而只是那些只有最低優先級的可行性。此方法與文獻[19]中應用于飛行器的鏈式分配法大同小異，其算法步驟如下：

步驟1：

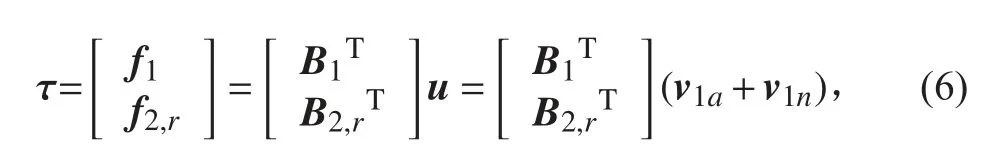
式中：f1為第1優先級需要產生的力矩。如果步驟1的分配已經滿足要求，計算將結束，并且f2,r為0，如若不滿足要求，將跳到步驟2。

步驟2：

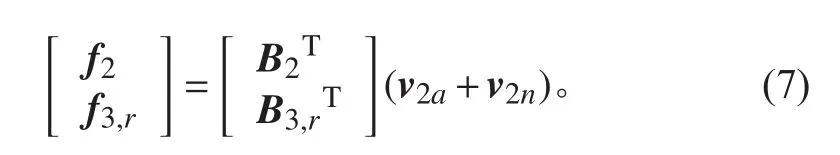
如果步驟2仍然不滿足，將會產生步驟3，以此類推，直到滿足分配要求，或者無法再繼續分配為止。這樣就保證了即使超出了執行器約束，船舶總體上仍然會朝著期望的方向運動，違反的只是低優先級的分配。此方法在一艘極地航行的船舶上進行了實驗，效果良好。

3.4 數學規劃法

數學規劃法也是常用的控制分配方法，可將控制分配問題轉化為線性規劃問題。序列二次規劃方法（Sequential Quadratic Programming，SQP）是其中求解約束問題的最有效方法之一。其基本思想是：在每一步迭代步驟通過求解一個二次規劃子問題來確立一個下降方向，以減少價值函數來取得步長，重復這些步驟直到求得原問題的解。文獻[14，20]中就使用了二次規劃分配法。

數學規劃法是以某一個優化目標函數而設計的一種方法，用此方法求得解能達到最優，并且在滿足約束以及其他要求的情況下能夠保證分配精度。

4 水下機器人控制分配

目前，已經開發出了功能各樣水下機器人，用于滿足各種不同的作業需求。常見的有載人潛水器；ROV，即遙控無人潛水器，無人水下航行器的一種，通過臍帶纜與母船連接，母船為其提供能源，功能多種多樣。AUV，其自帶能源，自推進，自主控制的潛器，不需要母船為其供電，通過自身攜帶的能源，航程從幾十千米到幾千千米不等。3.2節提到的偽逆法也應用于水下機器人。

4.1 加權偽逆再分配法

Edin Omerdic和Geoff Roberts[21]在2004年針對ROV提出了一種加權偽逆再分配法。首先假定推力大小與輸入為線性關系，并且執行器產生力矩u與期望力矩τ的映射關系也為線性，表示為：

首先根據推進器的布置與安裝情況求出操縱矩陣B，在矩陣B中加入W權重矩陣，用偽逆法求出一個可行解：

在2016年的印度控制會議上，Mohit.achada等[22]提出了一種加權力矩分配方法，用于控制分配，并且對超出約束的分配結果進行截斷處理。

4.2 數學規劃算法

數學規劃法不僅應用于船舶控制分配中，也應用于水下機器人。文獻[23]將其用于7 000 m載人潛水器有約束非線性控制分配，并且其采用的半物理仿真平臺實驗表明該優化控制分配算法的正確性和有效性，在控制量過大時，該算法可以給出穩定的優化解。文獻[24]將其用于舵槳聯控式水下機器人容錯控制，對比于單純的加權偽逆法，能夠解決控制量超出飽和限制的問題。

4.3 不動點迭代法

不動點迭代法是研究較多的方法之一，它利用遞歸不動點緊縮算法，易于編程實現，對于大多數輸入指令是快速而有效的。Omerdicd等將此方法用于過驅動的URISROV。小型AUV都不會裝備太多的推進器，因為其攜帶的能源有限，為了滿足操縱性要求，一般會裝備水平舵與垂直舵，也有裝備X-舵的AUV，擁有4個可以獨立運作的舵葉，直接對其舵角進行控制分配。張英浩等[11]針對X-舵的運動控制提出了一種基于Levy flight理論的控制分配方法，并且與基于偽逆不動點迭代的控制分配方法做了對比。迭代格式為：

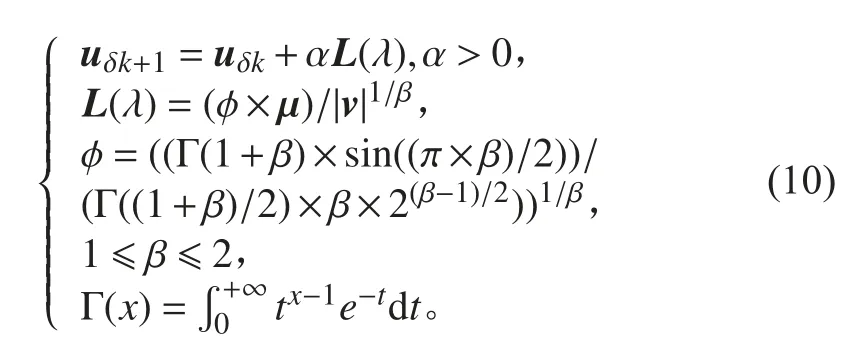
式中：μ，v 為隨機矩陣。基于Levy flight理論的控制分配方法可以達到原先的偽逆迭代控制分配一樣的效果，但是卻減少了舵的操縱量。

4.4 智能分配法

智能分配是一種新型的控制分配方法，與數學規劃法不同，其不需要依賴目標優化函數的梯度信息，可以設計更接近系統實際情況的凸空間集搜索，收斂快，最終解的精度高，例如粒子群優化算法。但是智能控制分配算法計算量比較大，對硬件要求高。劉通[25]在研究氣墊船舵槳聯合控制分配問題上應用了粒子群優化算法。

除了以上分配方法，用于水下機器人的還有基于約束的控制分配[15]，以及Tarun Kanti Podder等[26]的將控制律與控制分配結合的分配方式。

5 結 語

水中航行器在控制分配技術應用了許多控制分配方法，例如偽逆法、偽逆再分配、數學規劃、不動點迭代等。在AUV的研究當中，航程是一個重要的指標，而控制分配方法的優劣可以很大程度上影響能源的消耗，將來必將對AUV、ROV的操縱性提出更高的要求，更多的過驅動水下機器人將被設計出來，因此有必要繼續研究控制分配技術。現階段水下機器人的控制分配還存在以下幾個問題：

1）將期望產生的力矩與輸入看作是線性關系，實際上多為非線性關系，這與實際情況不符。

2）推進器與推進器之間，執行器與載體的耦合效應沒有充分考慮。

3）沒有考慮執行器的動態約束，例如舵的偏轉速度，執行舵角越大，舵到達指定位置的時間越長。

對于將來控制分配技術的發展，智能控制分配有很大潛力，智能控制分配收斂速度快、精度高，結果一般能達到最優，而且適合解決控制分配當中的非線性問題。例如采用神經網絡的控制分配，擁有強大的非線性逼近能力。現在可用于控制分配的智能算法包括神經網絡、粒子群優化、遺傳算法等。但是人工智能對硬件要求比較高，而水下機器人搭載的硬件設備少，性能不夠高，如何將人工智能融入到控制分配中，還需要更多的研究。