船體阻力數值預報研究及黏性流場計算

王英第，陳彥臻，周偉健，張盛龍

(1. 渤海船舶職業學院 船舶工程學院，遼寧 葫蘆島 125001；2. 上海海事大學 商船學院，上海 201306；3. 哈爾濱工程大學 動力與能源工程學院，黑龍江 哈爾濱 150001；4. 常熟理工學院 汽車學院，江蘇 常熟 215500)

0 引 言

自從能效設計指數（EEDI）標準實施以來，學者們紛紛開始關注船舶的能源利用和環境保護問題。在船舶運營中，燃料的消耗不僅和能源利用、環保等問題息息相關，燃料成本也是公司的巨大開銷之一。因此，設計出阻力更小的船舶以減少船舶運營成本、提高燃料利用效率，成為各國船舶研究人員的共同目標。能夠在設計階段準確預報出船體阻力變得非常重要。

隨著計算機技術的高速發展以及數值理論的日益成熟，昂貴的船模實驗開始漸漸被建立在仿真基礎上的設計方法所替代。近年來計算流體力學（CFD）方法得到了廣泛的認可，隨著許多優秀的CFD軟件如Fluent、CFX、SHIPFLOW等在工程問題中被大量應用，CFD方法體現出了其巨大價值，也使CFD方法應用于船舶阻力預報成為可能[1-3]。CFD方法能夠獲得與試驗數據相符的計算結果，同時計算周期短，成本低廉[4-6]。近年來，CFD方法已經成為計算船舶阻力的一種有效途徑，有相當多的CFD方法被應用在船體阻力預報中，基于CFD的數值計算成為一種新的經濟、高效的研究船舶水動力性能的工具。倪崇本[7]采用基于CFD理論的動網格技術對某多體船進行了數值模擬，探討了多體船船體姿態對船體表面壓力及船體附近波形等方面的影響。張艷等[8]利用CFD方法算得船身周圍水壓分布情況，并預測了水流對船舶產生的航行阻力。孔金平等[9]用CFD軟件對雙螺旋槳系統進行了數值計算，并采用湍流模型預報螺旋槳的水動力性能。

為了準確預報船體阻力，首先以自由模為例，討論了邊界層劃分方式及湍流模型中系數的選擇對阻力預報的影響。然后，在合適的網格方式上，采用NLPQL方法建立基于湍流系數的阻力優化系統來獲得最佳湍流系數。其次，根據最合適的網格劃分方式及數值計算方法模擬不同航速下KCS船在海面上的水動力性能，討論約束模和自由模在流場捕捉及阻力預報方面的差異。

1 CFD數學模型建立

整個CFD數學模型的流場控制方程由連續方程和運動方程構成。采用Realizable k-ε模型作為整個流場的湍流模型。采用VOF[10]方法精確捕捉自由水平面，VOF法是一種在固定的歐拉網格下的表面跟蹤方法，通過求解動量方程和一處或多處流體的體積分數來模擬多項流模型。采用SIMPLE法對壓力場和速度場進行耦合。

為了精確模擬KCS船在海面上的運動情況，將船體縱搖和垂蕩運動添加到阻力預報之中。在建立船舶運動方程時，建立2個參考坐標系：一個是固定于大地的固定坐標系，另一個是固定于船體的隨船動坐標系，其中動坐標系的原點在船體的重心處。

2 幾何模型及網格劃分

本文以KCS船型作為研究對象，該船的主尺度如表1所示。

整個計算域尺度設置為5Lpp×3Lpp×4Lpp。為了減小網格數量，取半船作為研究對象。在水池入口邊界給定船體航行速度，水池兩側設為對稱邊界，水池頂部和底部設為速度入口，出口處設為壓力出口，邊界條件設置如圖1所示。

切割體網格技術同時包含了非結構網格和結構網格的優點，對模擬大幅度物體運動問題具有較高的計算精度，是一種新發展起來的網格生成技術。本文采用切割體網格技術劃分計算域，網格劃分如圖2～圖4所示。圖2為整個流域網格圖，自由液面附近網格加密。圖3為船體及舵網格劃分圖，船體首尾及舵網格加密。圖4為自由液面網格劃分圖，船體附近網格加密，以準確捕捉船體周圍的流場。

表1 KCS船型主尺度Tab. 1 Principal dimensions of KCS ship types

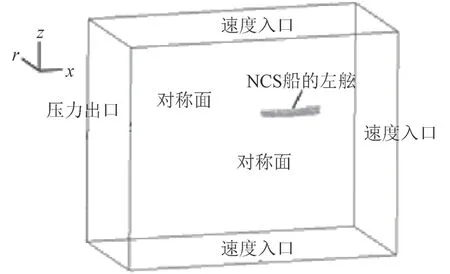
圖1 邊界條件設置Fig. 1 Boundary conditions

圖2 整個計算域網格劃分Fig. 2 Mesh on the computational domain

圖3 船體及舵表面網格劃分Fig. 3 Mesh on the hull and rudder surface

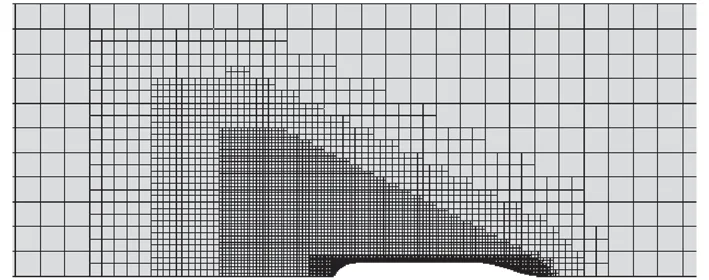
圖4 自由液面網格劃分Fig. 4 Mesh on the free surface

3 阻力預報流程

以KCS為例，采用RANS法模擬不同航速下船體水動力性能，其中船體分別設置成約束模和自由模，具體計算流程如圖5所示。

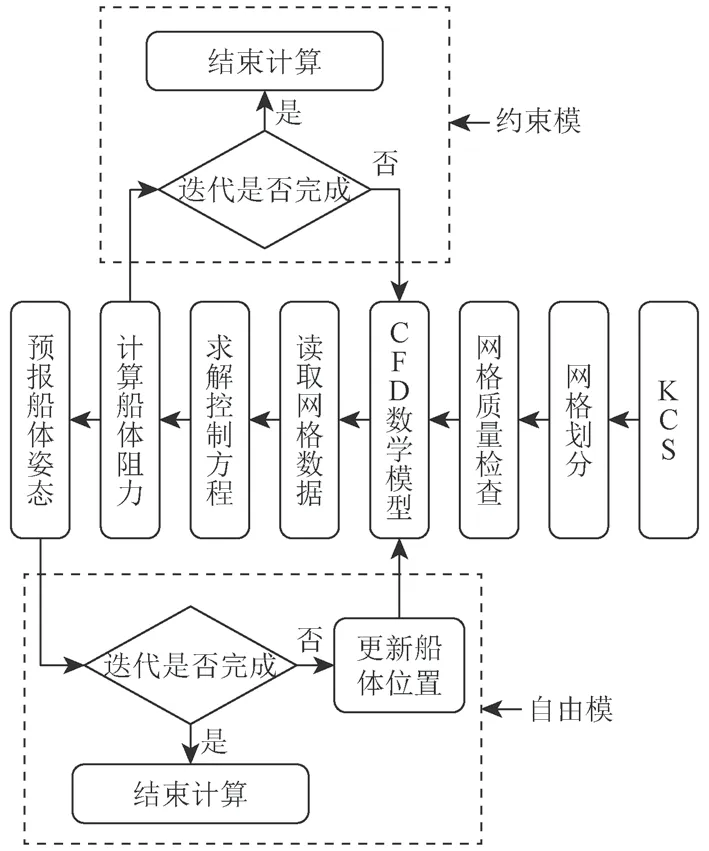
圖5 計算流程圖Fig. 5 Computational flow chart

4 CFD模型參數影響分析

4.1 邊界層對阻力的影響

船體在水中直航時，船體壁面附近會受到流體黏性的影響。對于黏性很小的空氣和水來說，黏性對流動的影響僅限于貼近船體表面的一個薄層內，這一薄層以外的黏性影響可以完全忽略。因此，為了準確預報KCS船型阻力，這一層網格的劃分顯得非常重要。以無因次參數y+表示船體表面第1層網格節點的高度，計算公式為：

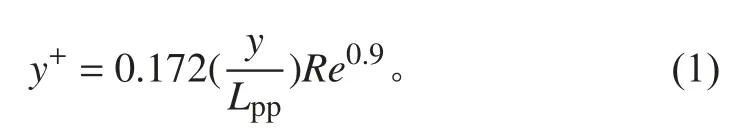
式中：y為第1層網格節點距離船體表面的高度（首層邊界層厚度）；Lpp為船體垂線間長；Re為相對船體長度所定義的雷諾數；y+取值范圍在30～200。

在邊界層網格劃分中，首層邊界層厚度、網格增長因子和邊界層數決定了網格劃分方式。因此，按照這3個因子依次討論邊界層劃分方式與阻力之間的關系，計算結果如表2～表4所示。

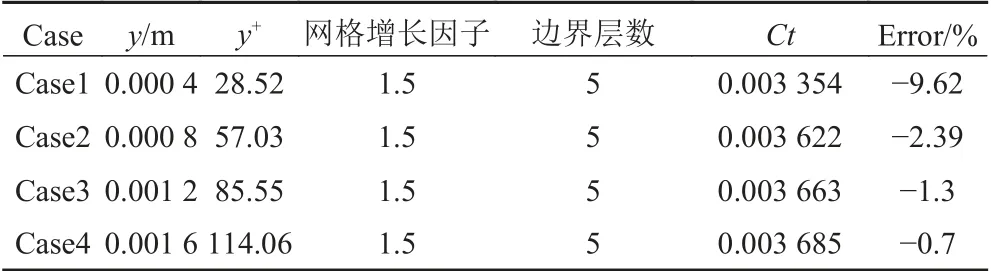
表2 首層邊界層厚度與阻力之間的關系Tab. 2 The relation between the thickness of the first boundary layer and the resistance

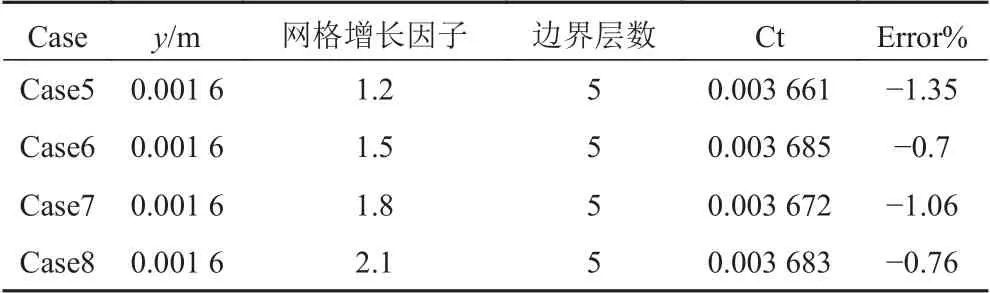
表3 網格增長因子與阻力之間的關系Tab. 3 The relationship between grid growth factor and resistance

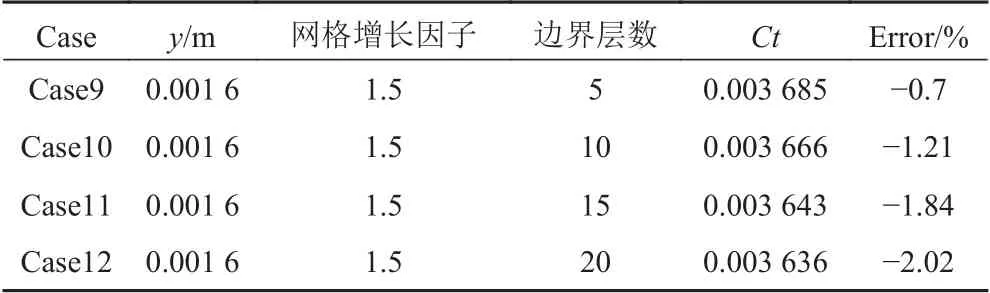
表4 邊界層數與阻力之間的關系Tab. 4 The relationship between the number ofboundary layers and resistance

從計算結果可以看出，誤差變化幅值均低于10%。其中，總阻力隨著首層邊界層厚度的增加變化明顯，而隨著網格增長因子和邊界層數的增加變化較小。隨著首層邊界層厚度的增加，船體總阻力增加；隨著邊界層數的增加，船體總阻力減小；而網格增長因子與船體總阻力之間沒有明顯的線性關系。從表3可以看出，當網格增長因子為1.5時，計算結果與實驗值更接近。

4.2 湍流系數對阻力的影響

根據經驗，網格數量的增加會提高阻力預報的準確性。但是隨著網格數量的不斷增加，計算效率將大大降低，并且網格數量增加到一定程度反而導致計算精度下降。所以在合適的網格數量上探討高精度的求解方式成為CFD數值模擬的關鍵。

雖然許多湍流模型已經取得了一定計算效果，但迄今為止仍舊沒有得到有效而統一的湍流模型，并且在分析湍流模型方程的一系列參數對計算結果及不確定度的影響這方面，很少有學者進行深入研究。因此，以Realizable k-ε模型作為研究對象，其中該模型的推薦計算值如表5所示。在湍流系數取值范圍附近改變取值并分別用來計算船舶阻力，其計算工況及阻力結果如表6～表10所示。

從計算結果可以看出，隨著湍流系數的變化，船體總阻力變化范圍在2.5%以內。隨著Cμ和αk的增加，船體總阻力減小；隨著C2ε和αε的增加，船體總阻力增加；而隨著C1ε的增加，阻力計算結果沒有明顯的線性關系。當C1ε＞1.42時，阻力隨著C1ε的增加而減小。

表5 Realizable k-ε湍流模型系數Tab. 5 Realizable k-ε turbulence model coefficients

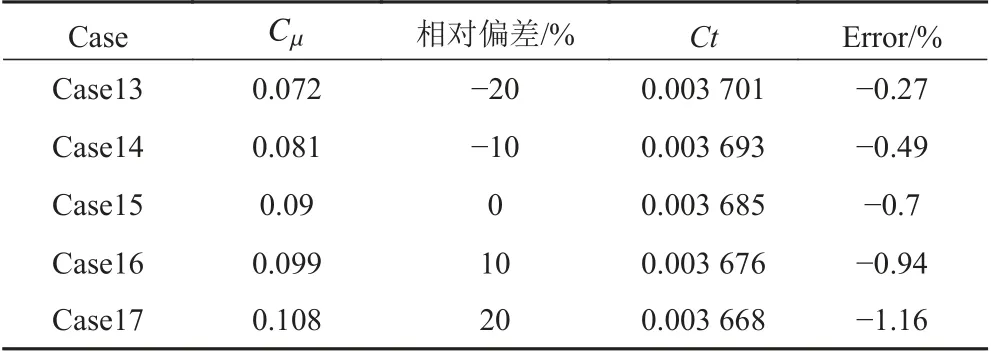
表6 Cμ與阻力之間關系Tab. 6 The relationship between Cμ and resistance

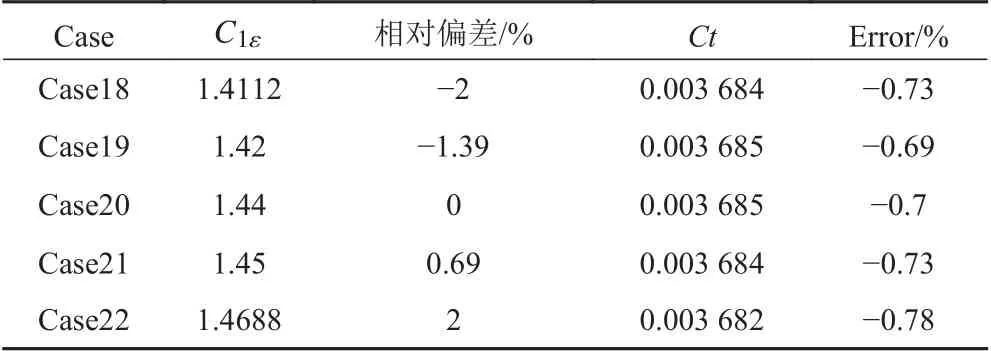
表7 C1ε與阻力之間關系Tab. 7 The relationship between C1ε and resistance

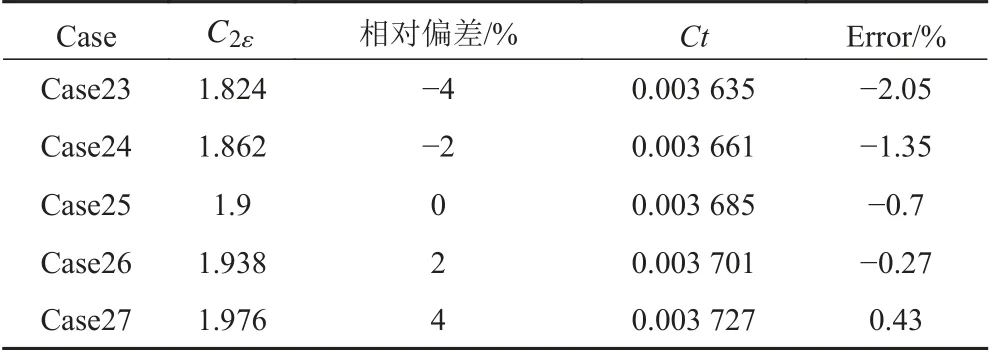
表8 C2ε與阻力之間關系Tab. 8 The relationship between C2ε and resistance

表10 αε與阻力之間關系Tab. 10 The relationship between and resistance

Caseαε 相對偏差/%CtError/%Case330.96-200.003 64-1.91 Case341.08-100.003 665-1.24 Case351.200.003 685-0.7 Case361.32100.003 695-0.43 Case371.44200.003 7230.32

5 模型參數優化及多航速阻力預報

5.1 模型參數優化

為了尋找到更適合KCS船體阻力預報的湍流系數，構建基于NLPQL算法[11]的優化系統。由之前的討論可以看出，C2ε和αε對阻力的影響較大，而C1ε和αk的變化對阻力影響較小。為了減小設計變量提高優化效率，固定C1ε=1.44，αk=1.0，選取其余3個參數作為優化設計變量。目標函數||RtCFD-RtEFD||為最小值。優化流程圖如圖6所示，優化過程如圖7所示。最優解集如表11所示。可以看出，經過一系列的優化得到了最優湍流系數。按照最優解計算的總阻力與實驗值最接近，誤差僅有0.054%。

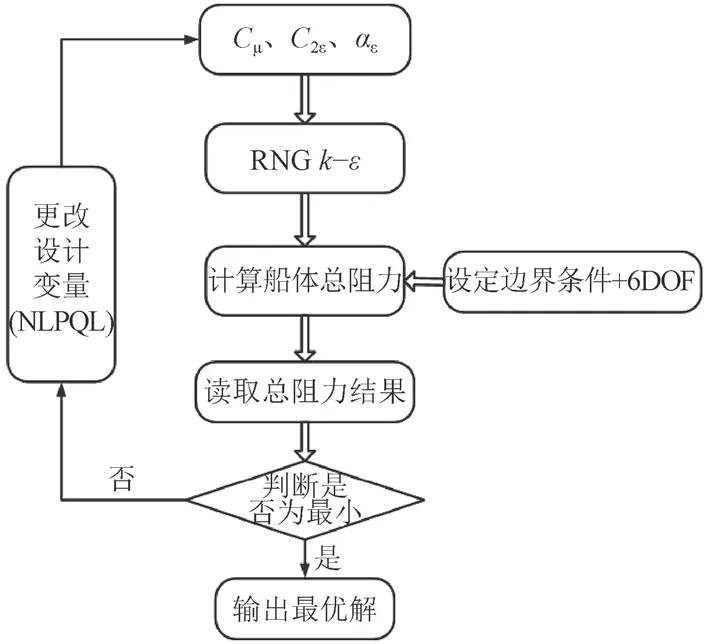
圖6 優化流程Fig. 6 Optimization process

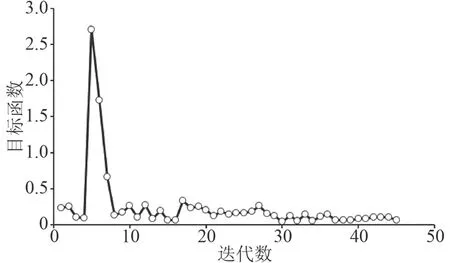
圖7 序列二次規劃算法優化過程Fig. 7 The optimization process for the NLPQL algorithm

表11 模型系數選取Tab. 11 The selection of Realizable k-ε turbulence model coefficients

5.2 多航速阻力預報

通過以上研究與討論，明確了船體阻力預報的邊界層劃分方式和最優湍流系數取值，以下采用該方法預報KCS船在靜水中直航的總阻力。

分別根據推薦系數和最優系數對船體總阻力進行預報，表12給出了CFD計算結果與實驗值的對比。可以看出，船體設置成自由模型比約束模型計算精度高，平均誤差為0.95%。且在高航速時，約束模型誤差較大而自由模型阻力預報值與實驗值吻合較好，誤差只有1.38%。

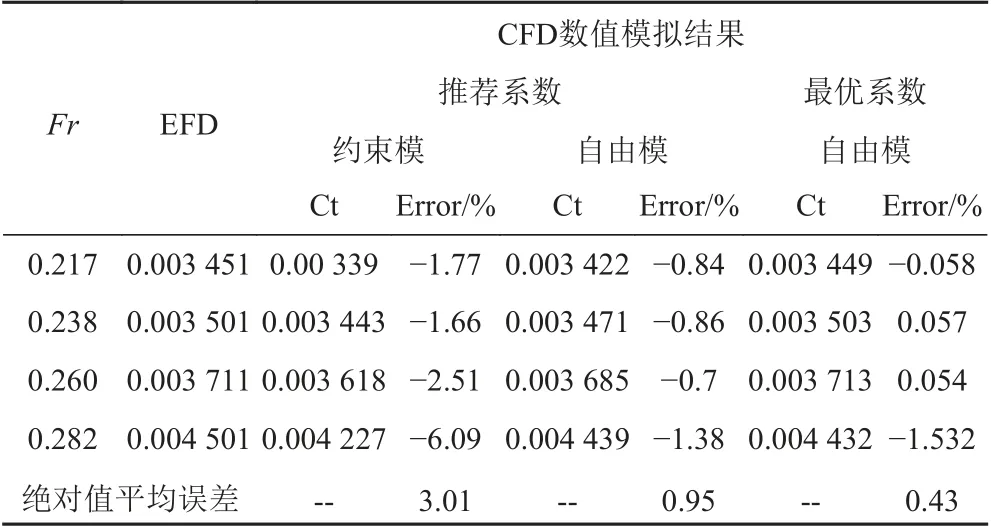
表12 總阻力計算結果與實驗值對比Tab. 12 The comparison of the Ct calculated by CFD and EFD methods

圖8和圖9為船體表面壓力分布圖。從圖中可以發現，在每個航速下，船體表面壓力等值線分布變化不大，但在球鼻首部分壓力等值線有明顯的不同，此處產生的壓阻是興波阻力的主要組成部分。由此可知，只有考慮了船體自身的運動姿態才能更全面的反應船體實際航行特性。在自由模計算中，最優系數在船體總阻力預報上平均誤差只有0.43%以內，而推薦系數的阻力計算結果誤差在0.95%。可以看出，最優系數在阻力預報精度明顯高于推薦系數，只有在Fr=0.282時計算結果較差，以此驗證了該湍流系數在多航速船體阻力預報上的實用性與可靠性。

圖8 船首表面壓力分布（約束模—推薦系數）Fig. 8 Static pressure distribution on the bow section（restraint mode-recommendation coefficients）

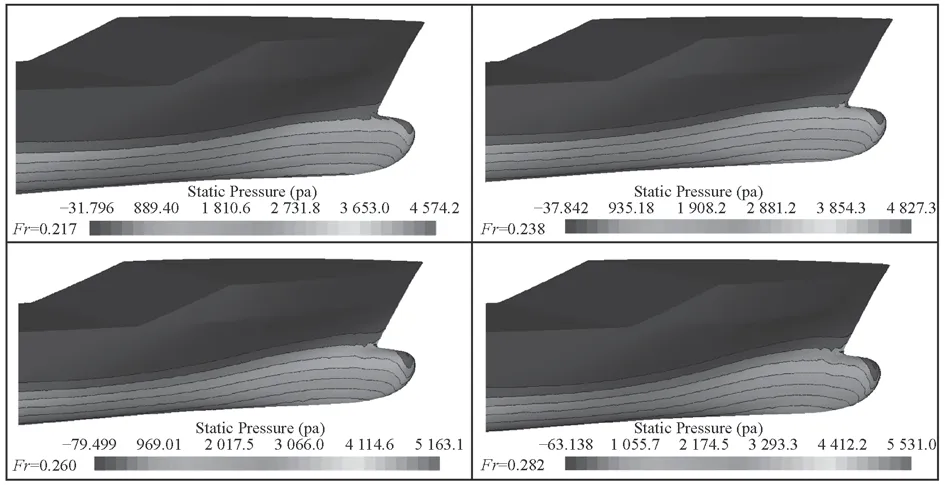
圖9 船首表面壓力分布（自由模—推薦系數）Fig. 9 Static pressure distribution on the bow section（free moderecommended coefficients）

表13給出了船體穩定時刻的縱傾角度和垂蕩位移隨Fr變化的數值大小。可以看出，本文計算結果與文獻[12]中的計算結果較吻合。隨著航速的增加，船體升沉明顯增大，而縱傾角增加較為緩慢。圖10為計算穩定時刻船體航行姿態。

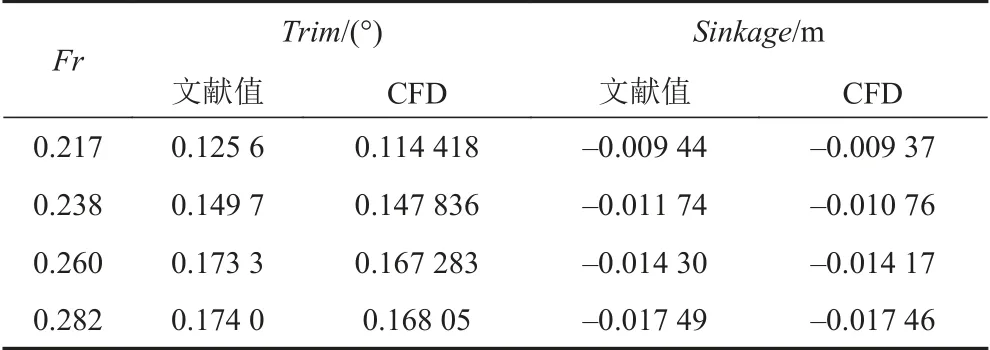
表13 縱傾值和垂蕩變化值與文獻值對比Tab. 13 The comparison of pitch and heave values obtained by CFD method and previous literature

圖10 穩定時刻船體姿態（自由模—最優系數）Fig. 10 Ship attitude at stable time（free mode-optimal coefficients）

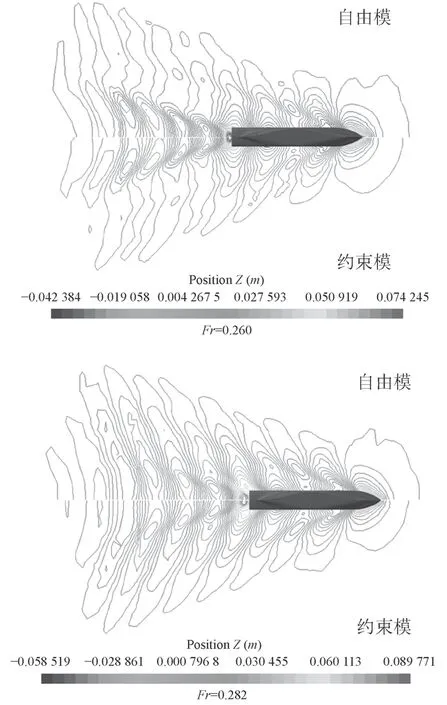
圖11 推薦系數波形等高線對比圖Fig. 11 The comparison of the waveform contour obtained by recommended coefficients

圖11為采用推薦系數計算的自由模與約束模波形等高線對比圖。可以看出，2種方法均能較清晰地捕捉到船體周圍的波浪形狀，說明VOF方法在自由液面捕捉上的優勢。雖然2種波形圖相似，但是在船首附近的波形相差較大。這主要是由于穩定后自由模在流場中的航行姿態與約束模不同，使得自由模的船體首尾壓力差大于約束模。圖12為采用自由模計算的KCS船波形等高線對比圖。可以看出，在Fr=0.282工況下波形等高線較為相似，而在Fr=0.260時波形等高線差別較大。這與表12中阻力計算結果相符。可見波形等高線的捕捉同樣可以作為船體阻力預報正確與否的評價標準之一。

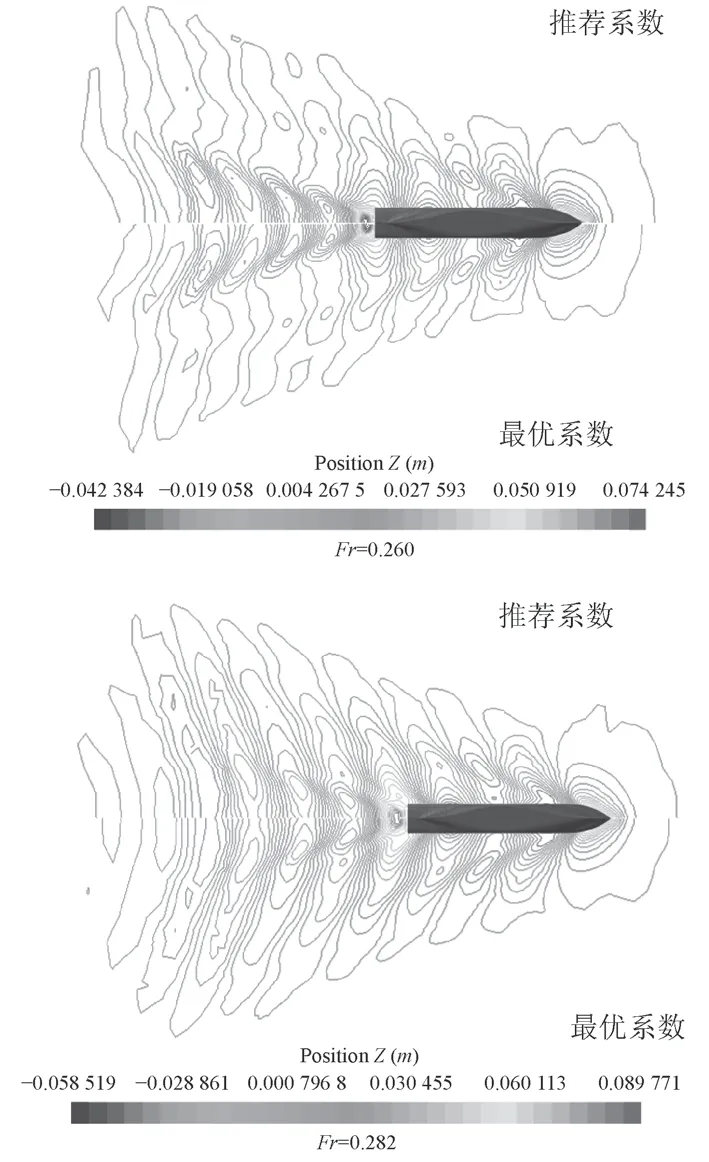
圖12 自由模波形等高線對比圖Fig. 12 The comparison of the waveform contour obtained by free-mode

6 結 語

本文采用SIMPLE算法求解不可壓縮RANS方程，對KCS船在靜水中的阻力預報精度進行研究，模擬了不同Fr時KCS船受到的總阻力、船體表面及周圍流場分布情況。結果表明：

1）船體附近邊界層劃分方式對阻力預報有較大的影響。隨著首層邊界層厚度的增加，阻力也隨之增加；隨著邊界層數的增加，阻力減小；而網格增長因子與阻力之間沒有明顯的線性關系。

2）C2ε和αε對阻力的影響較大，而C1ε和αk的變化對阻力影響較小。隨著Cμ和αk的增加，阻力減小；隨著C2ε和αε的增加，阻力增加；而C1ε與阻力之間沒有明顯的線性關系，但當C1ε＞1.42時，阻力隨著C1ε的增加而減小。其次，構建了基于NLPQL法的優化系統，得到了適合KCS船體阻力預報的湍流系數：Cμ=0.09，C1ε=1.44，C2ε=1.950 5，αk=1.0，αε=1.187 5。

3）自由模在船體阻力預報精確度上優于約束模，誤差只有0.95%。采用最優湍流系數對船體阻力進行預報時，除了Fr=0.282以外，其他航速阻力計算精確度均高于推薦湍流系數。