地下管線在地表爆炸荷載下的位移響應與參數分析

王亞光， 廖晨聰， 張 琪

(上海交通大學 土木工程系； 海洋工程國家重點實驗室， 上海 200240)

隨著我國城市規模的不斷擴張，地下管線作為城市生活功能的主要設施在全國范圍內大量鋪設.此外，我國大型暗埋管道工程如南水北調以及西氣東輸等工程中，地下管道承擔著運輸石油、天然氣以及水資源等的重要作用.然而，目前大部分管道暗埋深度較淺、地理跨度較大，所處環境復雜.管道周邊地面爆炸，比如汽車炸彈、戰爭爆炸以及意外爆炸都可能對既有管線造成不同程度的破壞.一旦管道發生破壞，管線內運輸資源的泄漏就會帶來巨大經濟損失及環境問題.因此，對既有管線進行爆炸荷載下動態響應的評估尤為重要.

在以往的地下頂管設計中，往往僅考慮管道內部荷載、穿越地質條件以及埋設方式等因素，較少評估地面爆炸等高度非線性荷載的影響[1].劉建民等[2]通過數值計算分析了埋地管道在淺埋爆炸和地面爆炸荷載下的動態響應.梁政等[3]和Yang等[4]應用LS-DYNA軟件分析了地下隧道在地表爆炸荷載下的結構響應，分別討論了藥量、管道壁厚等參數以及結構脆弱區范圍的問題.Wang等[5]通過SPH與FEM方法的聯合應用分析了地下結構物在淺埋爆炸荷載下的動態響應.Jiang等[6]研究了地表爆炸對既有地下結構的環境影響，建立了隧道單元和圍巖單元之間相對速度和有效拉應力的關系.Shin等[7]以隧道振動為主要觀測指標分析了側向爆炸對于巖石中隧道的影響.但是上述研究中均忽略了土中孔隙水的作用.Yu等[8-9]對隧道在爆炸荷載下的響應做了深入研究，側重分析了爆炸導致的振動對結構帶來的影響.Kouretzis等[10]在忽略了土-結相互作用基礎上，推導出柔性管線分別在P波和瑞利波作用下的管線應變,但該解析解簡化條件過多，應用有限.Feldgun等[11]基于耦合Godunov變分法，計算了土體-管線接觸應力，分析了飽和多孔介質中管線在側向爆炸荷載作用下的動態響應，其中孔壓分析是通過本構內嵌經驗公式所得，并沒有考慮水土相互作用.De等[12-13]通過離心機模型試驗以及數值模型分析了地面爆炸對于地下結構物的影響,研究了干砂中地下隧道維護材料的結構保護效果.Liao等[14]分析了動力荷載下的孔壓和液化，但荷載相比于爆炸工況則沒有很強的參考價值.Li等[15-16]利用數值方法分析了低非線性荷載對于地下結構物的影響.

由此可見，既有研究主要側重于爆炸振動對結構造成的影響，但忽略了土中孔隙水的作用.然而在我國東部沿海地區，鋼頂管等地下結構大多位于地下水位之下，孔隙水會對飽和土在動荷載下的響應產生不可忽視的影響[17]，忽略孔隙水壓力會使得計算結果產生一定偏差.因此，本文在前述研究基礎上，將u-p模型嵌入有限元程序，分析地下頂管在地面爆炸荷載作用下的響應，以結構位移為觀測對象，對炸藥當量、起爆位置、鋼頂管上覆土厚度、管徑等進行參數分析，以期對地下工程結構的設計施工提供有益的參考.

1 數值計算模型

1.1 高爆材料及理想氣體本構

地面爆炸荷載采用的是High_Explosive_Burn高爆材料模型和Jones-Wilkins-Lee(JWL)狀態方程模擬爆炸產物與比體積的關系.JWL狀態方程的表達式如下[18]：

(1)

式中：pt為爆炸產物的壓力；e為炸藥的內能；v為比體積；C1,C2,r1,r2,ω均為實驗確定的材料參數.本文中的炸藥采用TNT，參數如表1所示.表中：ρ為炸藥密度；vD為爆炸速度；pCJ為爆轟波陣面壓力；E0為單位體積炸藥內能；V為氣體體積.長方體炸藥位于地表，平面尺寸為1 m×1 m,通過改變炸藥材料高度模擬不同爆炸當量.

表1 TNT材料參數Tab.1 Material parameters of TNT

采用NULL空材料和線性多項式狀態方程描述爆炸作用下的空氣，其狀態方程如下：

pair=(0.4+0.4μ2)Eair

(2)

1.2 多孔介質本構方程和鋼頂管材料本構

多孔介質飽和度對于土體的動力響應影響顯著[19]，因此選取合適的土體本構模型對于計算精度與可靠性非常關鍵.本文選用了基于摩爾庫倫破壞準則的Federal Highway Administration (FHWA)模型[18]，該模型可以考慮土體的應變速率、應變軟化、隨動強化等特性，通過嵌入孔隙水壓力與有效塑性體積應變的經驗公式考慮孔壓特性.本文所得孔隙水壓力則是通過將u-p模型嵌入有限元程序，計算過程在下一小節中詳細描述.

研究表明，爆炸波的衰減速率隨著土體飽和度的上升而下降[20]，即飽和土中的地下結構相比非飽和土中的結構在爆炸荷載的作用下更加危險.考慮到大多數鋼頂管處于地下水位以下，同時為了計算模型的簡化，將土體模型視為完全飽和土.本文中選用的土體參數模擬長江三角洲地區的土體特性[21]，另外選擇理想彈塑性本構模擬鋼頂管在爆炸荷載下的響應，參數設置如表2所示.

表2 土體和鋼頂管參數Tab.2 Paremeters of soil and pipe jacking

1.3 u-p模型

土體是由土骨架，空氣以及孔隙水組成的多相介質，飽和土的動力學性質是由土骨架和孔隙水的相互作用決定的[17].考慮到土體在爆炸荷載作用下，孔隙水壓力的改變會影響土體強度，采用土骨架和孔隙水視為分別運動又相互作用的耦合方法更為適合.依據Biot流固耦合理論，土體介質由動量守恒方程、能量守恒方程以及質量守恒方程共同控制.

(3)

(4)

(5)

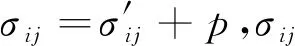
式中：M為全局質量矩陣；C為黏性阻尼矩陣；K為剛度矩陣；Q為耦合矩陣；G為動態滲流力矩陣；S為流體壓縮矩陣；H為滲透系數矩陣；U和P分別代表位移和孔隙水壓力向量；FP和FU分別為節點力和節點流量.

2 模型驗證

選取實驗數據[20]對數值模型進行驗證.驗證模型如圖1所示，炸藥埋置于地表以下2.5 m處，應力監測點水平分布于地表以下2.5 m處.在炸藥周圍2 m范圍內，爆炸會造成巨額能量的瞬間釋放，使得爆炸點毗鄰區域產生巨大變形，如果采用傳統的Lagrange算法，網格畸變后則會造成計算不收斂.所以在驗證模型中，距離炸藥附近2 m×6 m范圍內采用ALE算法處理爆炸引起的土體大變形問題，局部單元網格尺寸為20 cm，遠端土體模型采用Lagrange算法.模型左側為對稱邊界，底部單元節點固定，右側遠離爆炸端為固定邊界.由于爆炸現象的高度非線性，模型邊界設為不透水條件.通過應力初始化完成地應力平衡.

圖1 土中爆炸原型模型Fig.1 Prototype model for underground explosion

高爆材料的起爆會釋放巨額的能量，爆炸產生的高溫、高壓氣體會在相鄰介質中以爆炸波的形式向遠方傳遞.爆炸波在多孔介質中隨著傳播距離的增大呈指數衰減，在lgσmax-lgls坐標系下，衰減曲線為直線，其中σmax為峰值應力，ls為等效距離.如圖2所示，本文在驗證模型中通過10 kg(綠色)和30 kg(藍色)TNT當量的爆炸算例對模型進行校準.可以看到不同爆炸當量的模型計算所得峰值應力隨傳播距離均呈線性減小的趨勢，計算所得衰減曲線與實驗總結規律基本保持一致.在炸藥10倍半徑內，爆炸波的傳播速度遠高于介質聲速，同時，飽和土中的爆炸波傳播速度約為 1 200～1 500 m/s，很難捕捉到土體單元真正的應力峰值.所以考慮到計算結果的輸出間隔有限，計算所得土單元的峰值應力的衰減曲線整體上會略低于實驗規律，但誤差結果較小可以接受.因此，將基于本文模型對地下鋼頂管在爆炸荷載下動力響應的深入研究.

圖2 爆炸應力峰值衰減校準圖Fig.2 Peak pressure attenuation in saturated soil

3 結果與參數分析

對地下頂管的動力響應進行建模.如圖3所示，模型由炸藥、空氣、土體和鋼頂管組成.炸藥的平面尺寸為1 m×1 m，模擬地面汽車炸彈，在炸藥下方建立6 m×6 m×3 m的ALE土體區域.為了簡化計算模型，對頂管周圍土體采用一套參數，同時將地下水位設為與地表齊平.三維模型的邊界條件采取底部固定，左右兩側及前后兩側僅允許z向位移.同時由于爆炸荷載的高度非線性，傳播速度快，作用時間短，將模型邊界設為不透水邊界.研究參數為炸藥當量、起爆位置、埋置深度(觀測點至起爆點的z向距離)以及頂管管徑.

圖3 計算模型簡圖Fig.3 Sketch of calculation model

圖4分別為起爆點正下方6 m和15 m處的土體應力(σ)和孔隙水壓力(p)的時程曲線.可以看到孔隙水壓力與土應力的變化一致，在爆炸波波峰到達觀測單元時，土應力和孔隙水壓力驟升，稀疏波緊隨爆炸壓縮波之后，由于孔隙水不能受拉，孔隙水壓力瞬間消散，由于土體單元在爆炸波的作用下整體處于受壓狀態，最終在土體單元應力的波動中，孔隙水壓力又出現累積.

圖4 起爆點下方土體應力和孔壓時程曲線Fig.4 Time series of soil pressure and pore pressure below the explosion position

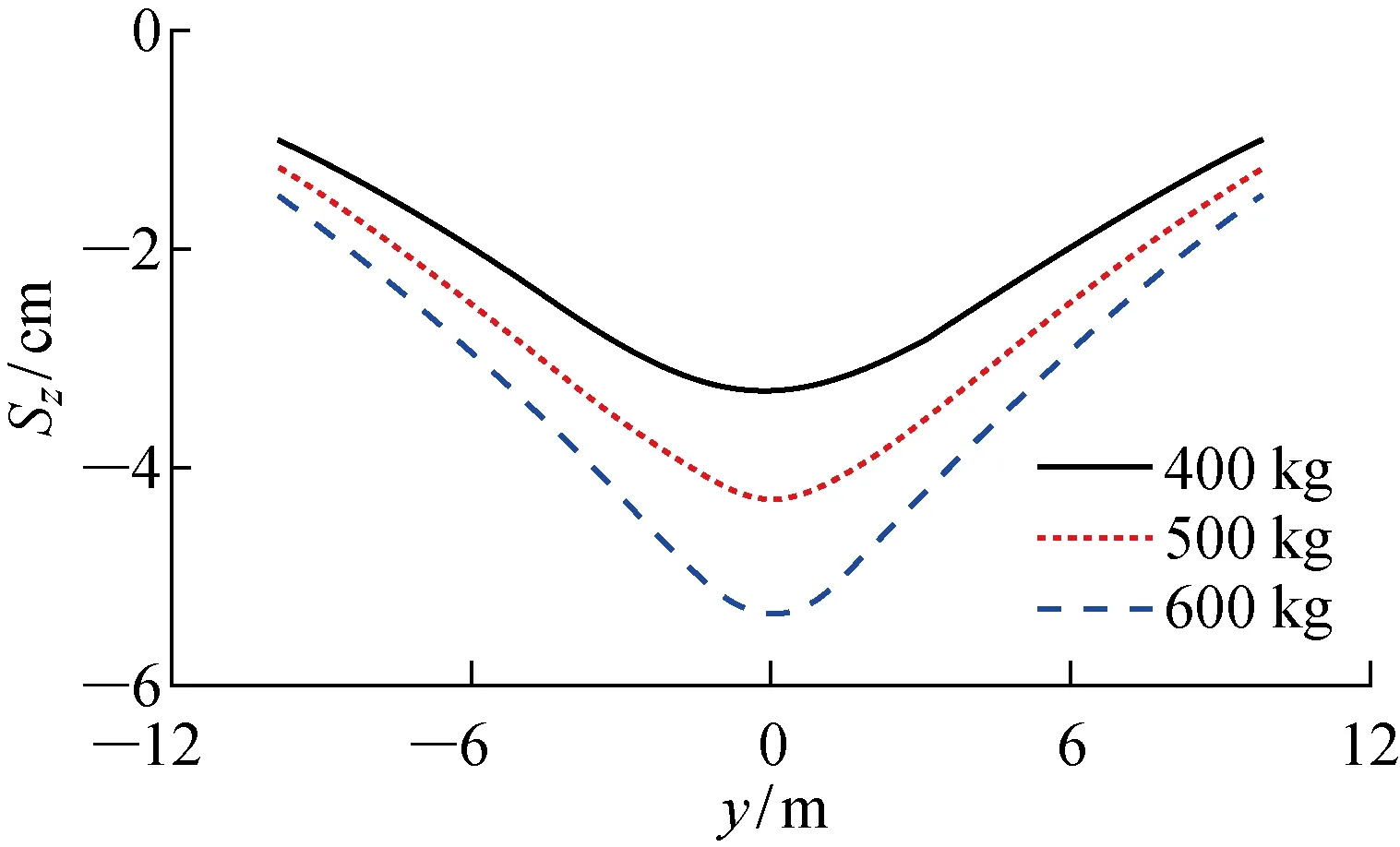
圖5 不同炸藥量下頂管最大豎向位移分布Fig.5 Distribution of peak z-displacement of pipe jacking under various explosive charges

首先分析炸藥當量對于鋼頂管的影響.在模型中，鋼頂管上覆土厚8 m，頂管半徑1 m，管壁厚2 cm.圖5所示為不同炸藥當量情況下頂管最大豎向位移(Sz)，其沿頂管軸向對稱分布，且隨炸藥量的增加而線性增大.當炸藥量達到600 kg時，頂管結構未出現位移突變，表明頂管仍在塑性變形階段，未達破壞階段.

爆炸波在土中指數衰減趨勢，故上覆土對頂管起到一定保護作用.基于600 kg TNT，半徑為1 m，管壁厚2 cm的鋼頂管模型研究埋深(D)對頂管動態響應的影響.如圖6所示，隨著上覆土厚度的增大，-5～5 m范圍內的頂管核心受壓區的豎向位移明顯減小.在目前爆炸當量下，埋深超過11 m時，上覆土對于鋼頂管的保護作用開始減弱.當埋深僅為5 m時，-3～3 m范圍內位移較大，而y=±5 m左右的頂管下方土體則起到了類似杠桿支點的效果，進而導致埋深5 m的鋼頂管在6 m范圍外的豎向位移反而較小.

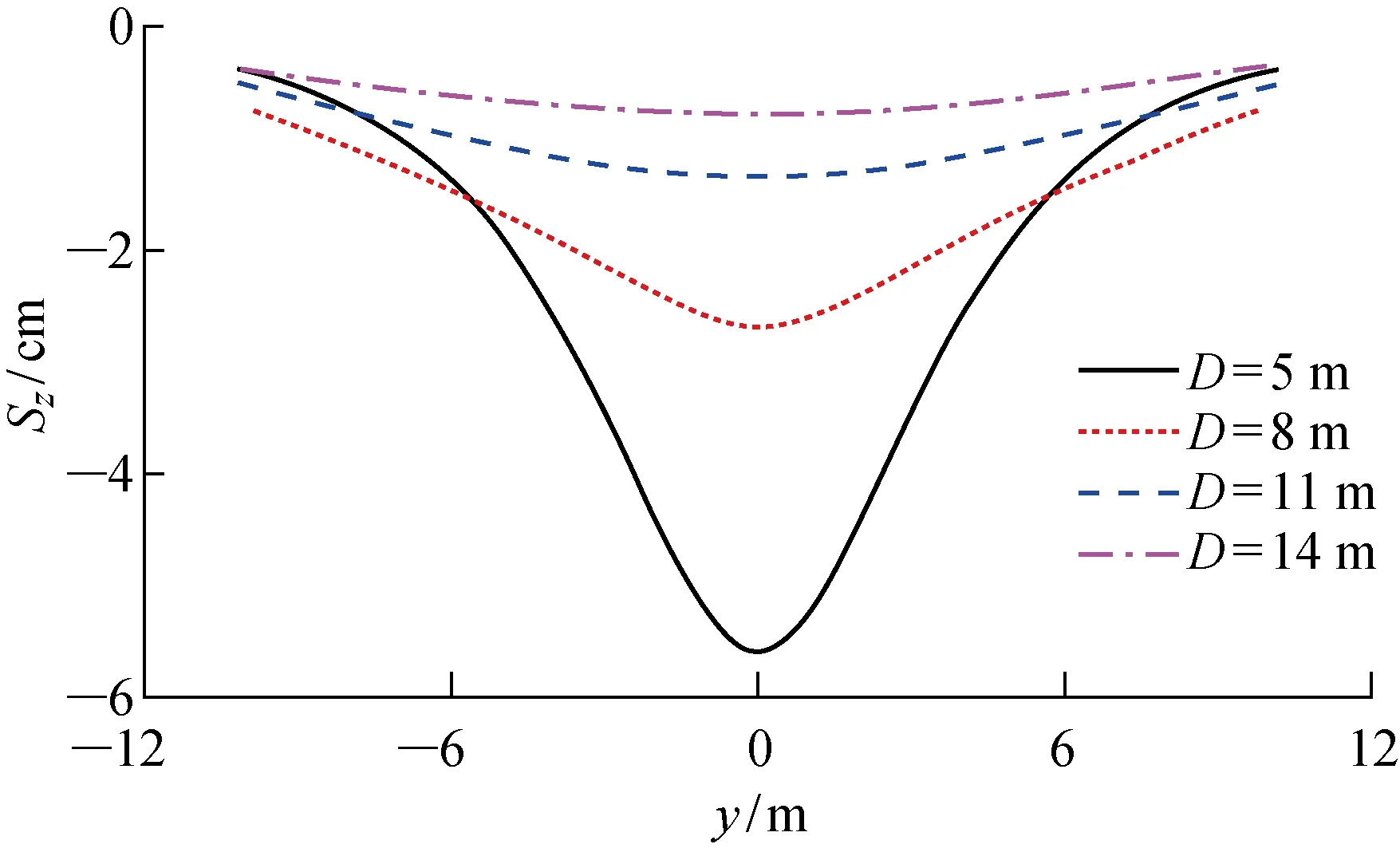
圖6 不同埋深下頂管最大豎向位移分布Fig.6 Distribution of peak z-displacement of pipe jacking under various embedment depths

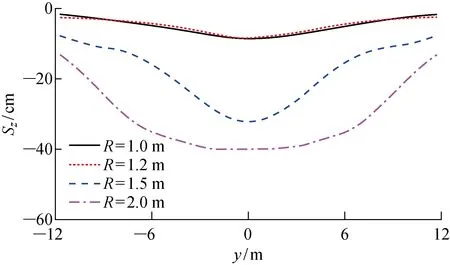
圖7 不同頂管半徑最大豎向位移分布Fig.7 Distribution of peak z-displacement of pipe jacking under various pipe jacking radii

頂管管徑(R)同樣會對結構的動態響應造成影響.從圖7可以看到，在頂管上覆土厚度為8 m，地面爆炸荷載為600 kg TNT當量的情況下，當頂管半徑小于1.2 m時，頂管最大豎向位移分布相似.當頂管半徑為1.5 m時，距離起爆點橫向距離5 m以內出現明顯塑性變形，并不斷發展，最終結構局部破壞.而當頂管半徑為2.0 m時，結構平面內結構破壞范圍進一步擴大.

當地表爆炸荷載真正出現時，往往不會在頂管的正上方，所以本文對起爆點的偏移位置進行了討論分析.研究模型中，鋼頂管埋深8 m，頂管半徑1 m，管壁厚度為2 cm，起爆點的偏移x=0，4，8，12 m，如圖8所示.當偏移距離小于4 m時，頂管的豎向位移分布模式相似.而當偏移距離大于8 m時，鋼頂管傾向于整體位移.需要指出的是，洋紅色實線是起爆點的偏移距離12 m時的頂管最大豎向位移結果，洋紅色虛線是起爆點偏移距離為12 m時頂管豎向位移最終穩定狀態.可以看到頂管沿軸向豎向位移最終穩定狀態(洋紅色虛線)為正.炸藥起爆后會在土體中產生體波和面波，體波傳入土體深處，按照運動方式又分為P波和S波.P波在多孔介質中衰減較快，僅能在起爆點鄰近土體中起到加固作用；而S波傳播較遠，會對土體產生擾動，同時爆炸區附近的土體壓縮對遠處的土中結構物起到了側向擠壓作用，這也就造成了偏移距離為12 m的算例中，最終穩定狀態時頂管略微上浮(洋紅色虛線).

圖8 不同起爆點偏移位置下鋼頂管最大豎向位移分布Fig.8 Distribution of peak z-displacement of pipe jacking under various explosion offsets

此外，起爆位置的偏移會對鋼頂管產生橫向推力.如圖9所示，起爆點在頂管正上方時，頂管也會產生少量的橫向位移(Sx)，整體豎向向下運動.在偏移距離增至8 m的過程中，頂管沿軸線的橫向位移逐漸變大，形態穩定.而當偏移距離為12 m時，在 -6～6 m范圍內，頂管整體平移，平移量略小于偏移距離為8 m的算例.

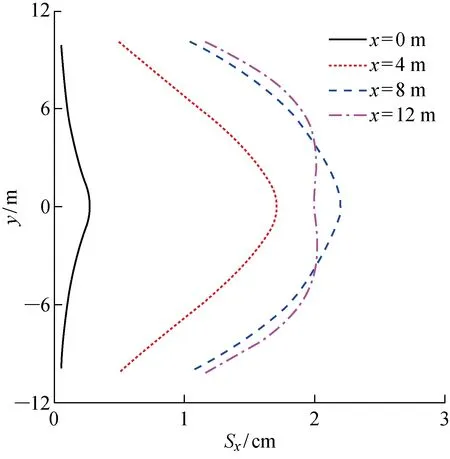
圖9 不同起爆點偏移位置下鋼頂管最大橫向位移分布Fig.9 Distribution of peak x-displacement of pipe jacking under various explosion offsets

4 結論

在本文中，通過將u-p模型植入有限元程序，實現水土耦合計算，建立了地表爆炸荷載作用下地下鋼頂管的動態響應模型，通過將ALE-Lagrange的耦合算法解決爆炸荷載導致的網格畸變問題，進而對飽和土中地下鋼頂管在地面爆炸荷載下的動態響應問題進行研究.隨后基于前人實驗規律對本文模型進行了驗證，最后對炸藥量、起爆位置、鋼頂管埋置深度以及頂管半徑等參數進行了參數分析.基于計算結果，可以得到如下結論：

(1) 將u-p模型嵌入有限元程序，實現了在高度非線性荷載作用下的水土耦合計算，可以用于研究沿海高地下水位地區地下結構物在爆炸荷載作用下的動態響應問題.

(2) 建立驗證模型，通過已有實驗數據對本文模型進行了驗證，應力波在飽和土中指數衰減，與實驗規律基本一致，證明了本文模型預測既有管線在爆炸荷載作用下的動態響應的可行性.

(3) 實驗結果表明，在地下鋼頂管結構局部破壞前，頂管豎向位移隨炸藥量線性增大；頂管豎向位移隨上覆土厚度的增大而減小，埋深設為11 m左右，上覆土對頂管的保護效果較好，同時保證施工經濟性.

(4) 頂管直徑的增大會降低結構在地表爆炸荷載作用下的承載能力，隨著埋深的增加需要對管線進行有效的力學分析，設計合理的管徑和壁厚.

(5) 頂管最大豎向位移隨起爆點偏移距離的增大而減小，當偏移距離為12 m時，頂管在爆炸波的作用下最終略微上浮，同時，頂管的橫向位移也會隨著偏移距離先增大后降低.