吸力錨吊裝入水動力學分析
李 俊,郭睿男,昝英飛,羅 超,郝高正
(1. 海洋石油工程股份有限公司,天津 300450;2. 哈爾濱工程大學 船舶工程學院,哈爾濱 150001)
0 引 言
吸力錨結構被廣泛應用于海底結構物的固定、海上風機樁腿和鋼懸鏈線立管安裝作業,是海上石油生產的重要基礎設施。利用起重安裝船垂直吊放的安裝方法在國內外應用廣泛[1]。Selv?g[2]對海底壓縮機模塊進行拘束規則波砰擊實驗,發現測量模塊受到的水平力和垂直力,并將實驗結果與Simulation of Marine Operations (SIMO)和Orcaflex的軟件結果進行對比,評估預報模塊砰擊載荷的準確性。陳勇等[3]基于Det Norske Veritas規范的結構物吊裝入水簡化算法獲得相應的動態放大系數,并與采用Orcaflex軟件的結果進行了對比分析。梁海青[4]利用有限元軟件FLUENT研究采油樹下放過程中動力學影響因素,最終確定采油樹安裝環境要求。周傲[5]以海底模塊的吊裝試驗為依據,驗證SIMO的模擬并進行結構物入水耦合響應仿真研究。Li等[6]利用SIMO程序建立船舶系留系統的耦合數值模型,計算了瞬態下降過程中閥芯上的砰擊載荷和浸沒載荷。Chilinski等[7]利用幅值響應算子(response amplitude operators,RAO)建立激勵函數計算船舶的運動,不考慮吊物和船舶的耦合,根據第二類拉格朗日方程推導三自由度的吊裝系統運動模型,進行重量和吊臂頂端位移的參數化研究,并研究規則和不規則波的響應。Naess等[8]研究了吸力錨經過飛濺區時空氣和水的相互作用,根據軟件ANSYS CFX求解附加質量并進行吸力錨吊裝的時域仿真。Ha等[9]通過實驗和時域模擬,研究在波浪中使用浮吊對浮托進行吊裝時不同載荷分配和不同波浪條件下起重機鋼索的動張力,并討論了樁腿的沖擊力。
吸力錨入水時大量空氣僅由通風孔排出,除控制速度外,開孔率不足將引發較大的浮力進而發生突變載荷或引發吸力錨的傾斜[10]。吸力錨的開孔會在空腔中和錨壁附近產生回流和大面積的渦[11]。因此吸力錨中空氣的狀態是吸力錨入水過程的重要影響因素之一。然而,關于空氣對吸力錨吊裝作業影響的研究尚不足,目前僅確定在通過飛濺區時為了避免較大的浮力,確保空氣被充分排出,必須在吸力錨的頂部安裝一個通風孔。為了避免較大的浮力可能導致吊索松弛,通風孔水平面積與錨頂的比值(開孔率)必須足夠[12]。
本文利用計算流體力學軟件Star-CCM+ 2020.1,基于雷諾時間平均navier-stokes (Reynolds-averaged navier-stokes,RANS)方程,對由四個吸力錨構成的結構物在可壓縮和不可壓縮空氣環境中的飛濺區吊裝作業進行研究。在評估結構物總體載荷的同時,進一步對可壓縮和不可壓縮空氣在吸力錨內的壓力進行分析,為將來吸力錨結構的載荷評估和結構優化提供參考。
1 數值方法
1.1 控制方程
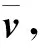
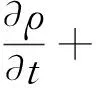
(1)
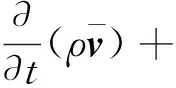
(2)
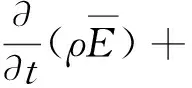
(3)
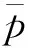
采用流體體積函數法(the volume of fluid,VOF)求解多相流,VOF的實現屬于預測非混合相界面分布和運動界面捕捉的方法。相的分布和界面的位置由相體積分數αi來描述。定義相i的體積分數為
(4)
其中:αi=0時,表示完全沒有相i;αi=1時,網格完全充滿了相i; 0<αi<1時,網格內存在相的交界面。
本文分別對可壓縮空氣和不可壓縮空氣進行建模,設定如下:
(1) 不可壓縮空氣,密度恒定,不使用能量模型。
(2) 可壓縮空氣,等溫模型,理想氣體,初始溫度為15℃,比熱比k=1。
(3) 可壓縮空氣,絕熱模型,初始溫度為15℃,比熱比k=1.4。
對于條件(3),雙原子氣體,如空氣,在絕熱條件時比熱比為1.4[14]。根據Tregde[15],初始空氣密度(ρg0)和壓強(p0),瞬時空氣密度(ρg)與壓強(p)的關系定義為
(5)
密度隨壓強的導數為
(6)
本文還做出如下假設: 研究中分別設置水和空氣的特性,對水進行建模時應用定常密度,從而保證水是不可壓縮的;假設結構物為剛體且不考慮水彈性效應。
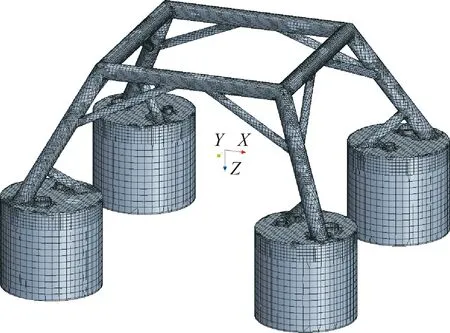
1.2 研究對象
考慮纜繩張力、網格精細度以及計算量,設定模型與實物間的比例尺為0.5。結構物模型主要由4個吸力錨和鋼管焊接形成的鋼架構成,模型高H為6.65 m,寬B為13.9 m,空氣中質量為25 t;吸力錨直徑為3 m,高2.75 m,錨壁厚0.01 m,設有兩個通風孔,直徑分別為0.305 m和0.51 m。重心距結構物底端3.281 m。選取起重機實際釋放速度為0.1 m/s,模型的釋放速度為0.07 m/s[16]。結構物模型、吸力錨的編號及隨體坐標如圖1所示。吸力錨尺寸相同,但通氣孔的布置并非對稱,如圖1(a)所示。固定坐標系位于重心正下方與吸力錨頂部的上表面等高的平面上,坐標軸方向與隨體坐標一致,如圖1(b)所示。模擬中吸力錨進行六自由度運動。
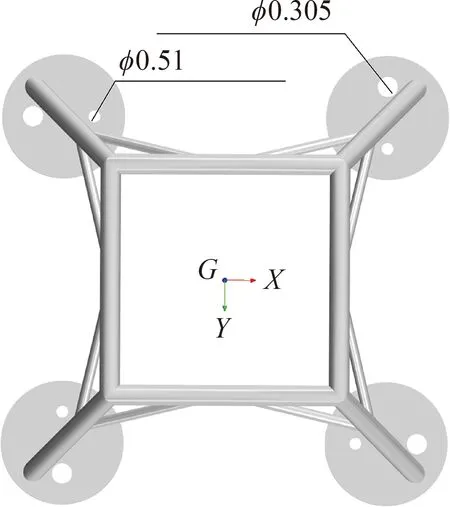
(a)
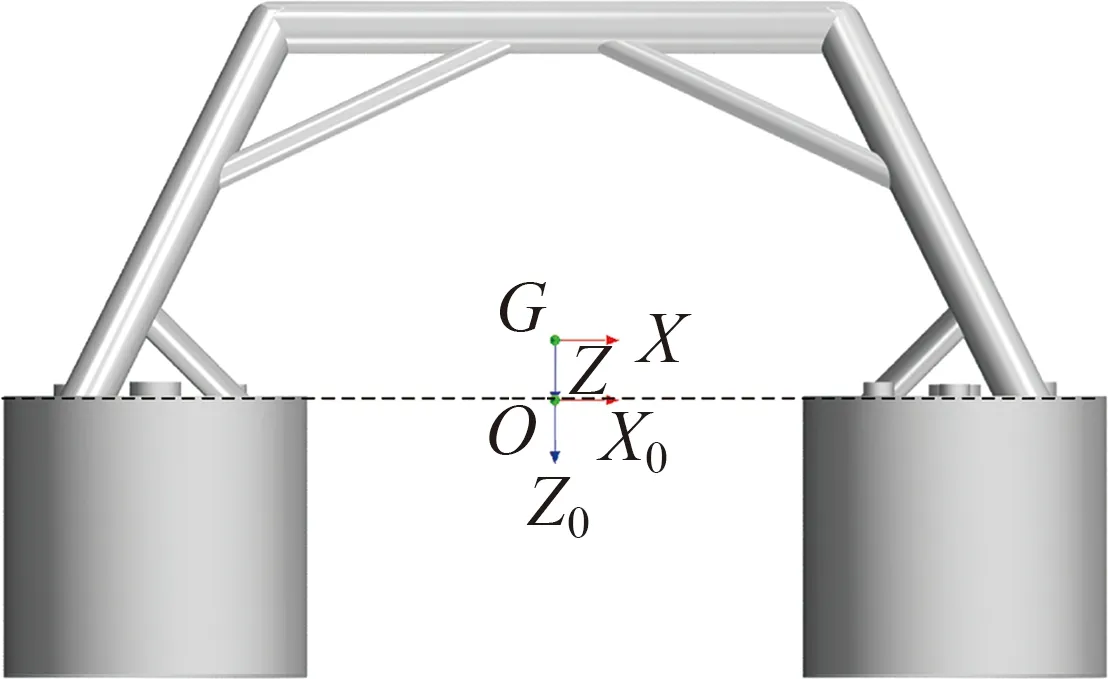
(b)
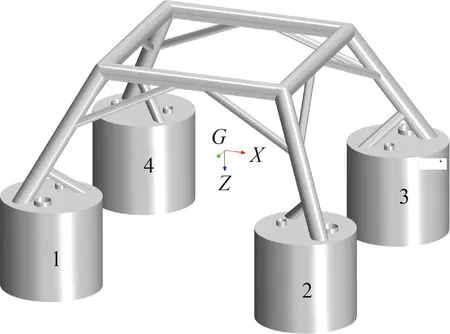
(c)
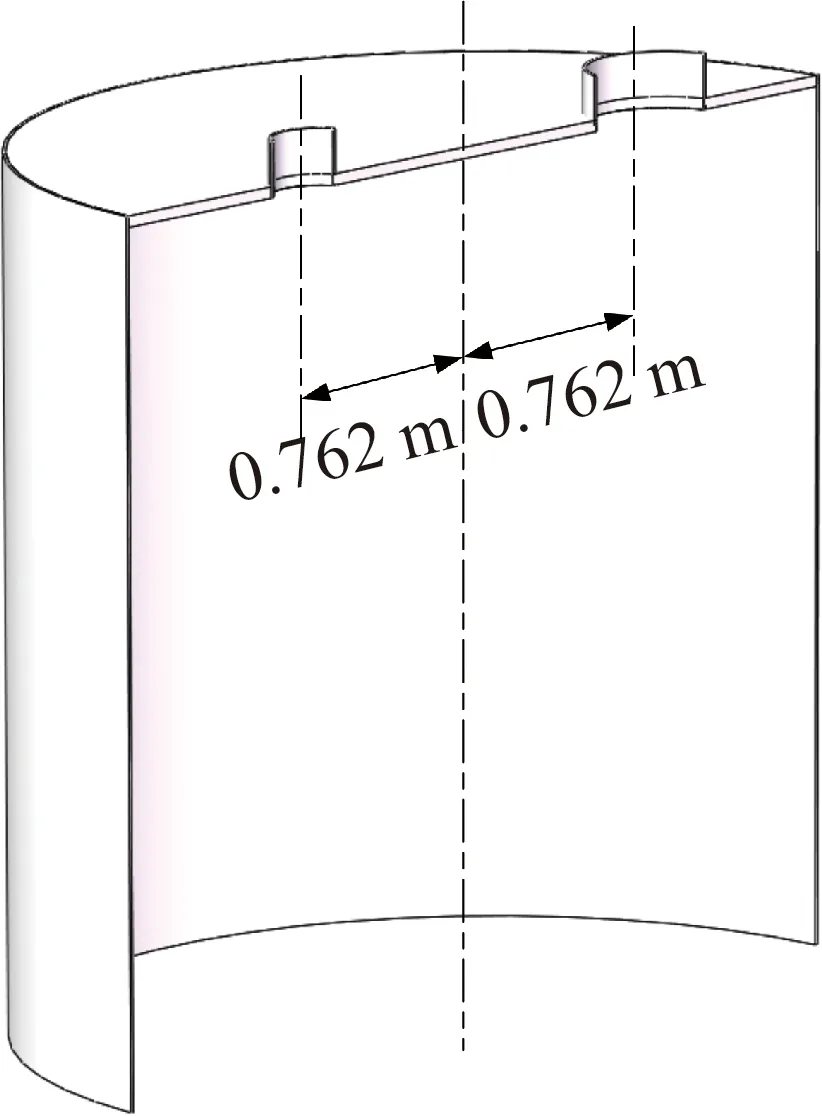
(d)
1.3 計算域與模型網格劃分
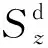
(7)
式中:f1和f2為一階和二階阻尼系數,nd為阻尼指數,xed為波浪阻尼區域的終點(邊界),xsd為阻尼區域的起點[見圖2(b)中的紅色矩形],x為阻尼區域[見圖2(b)中灰色區域]內水平方向的坐標。
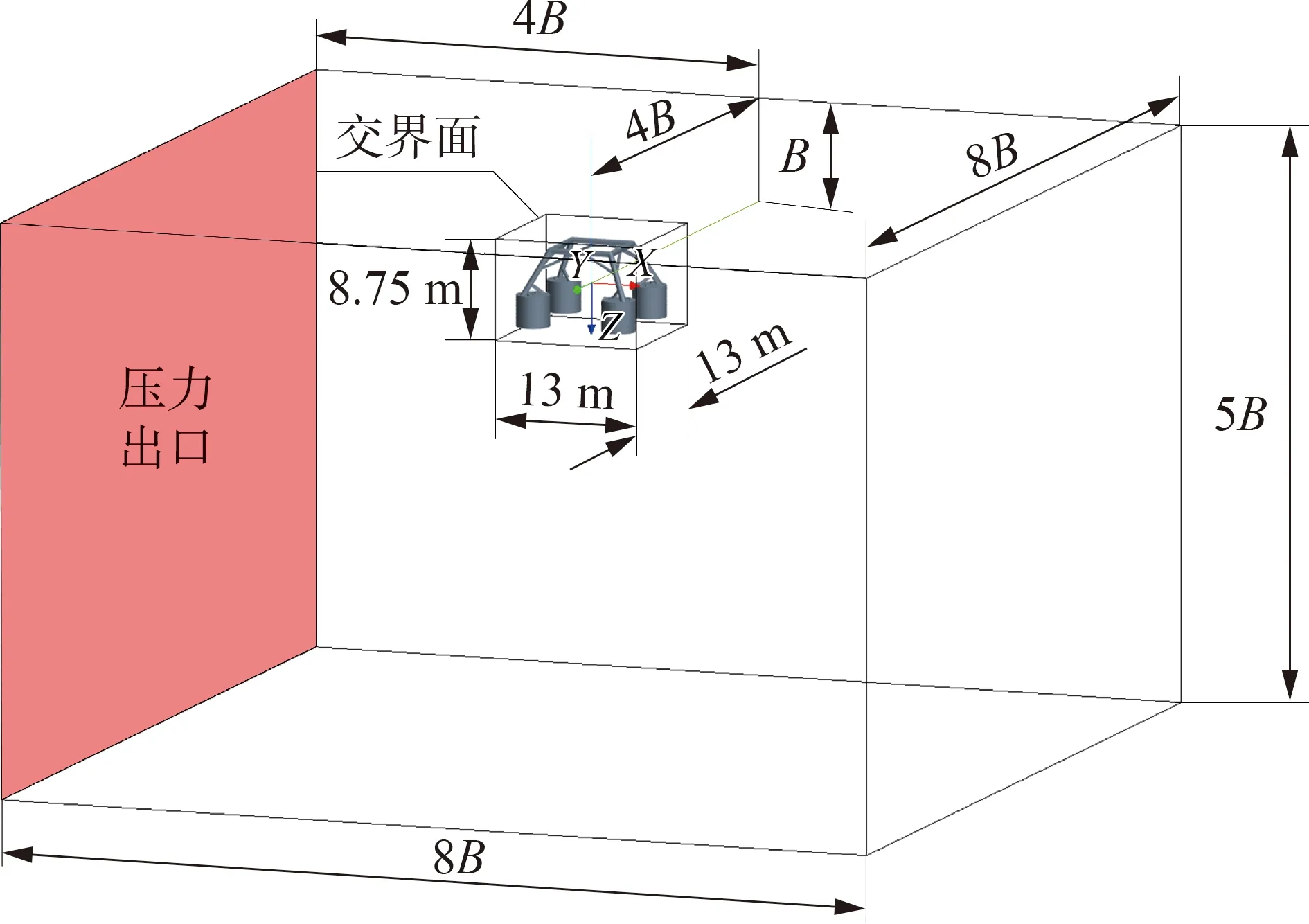
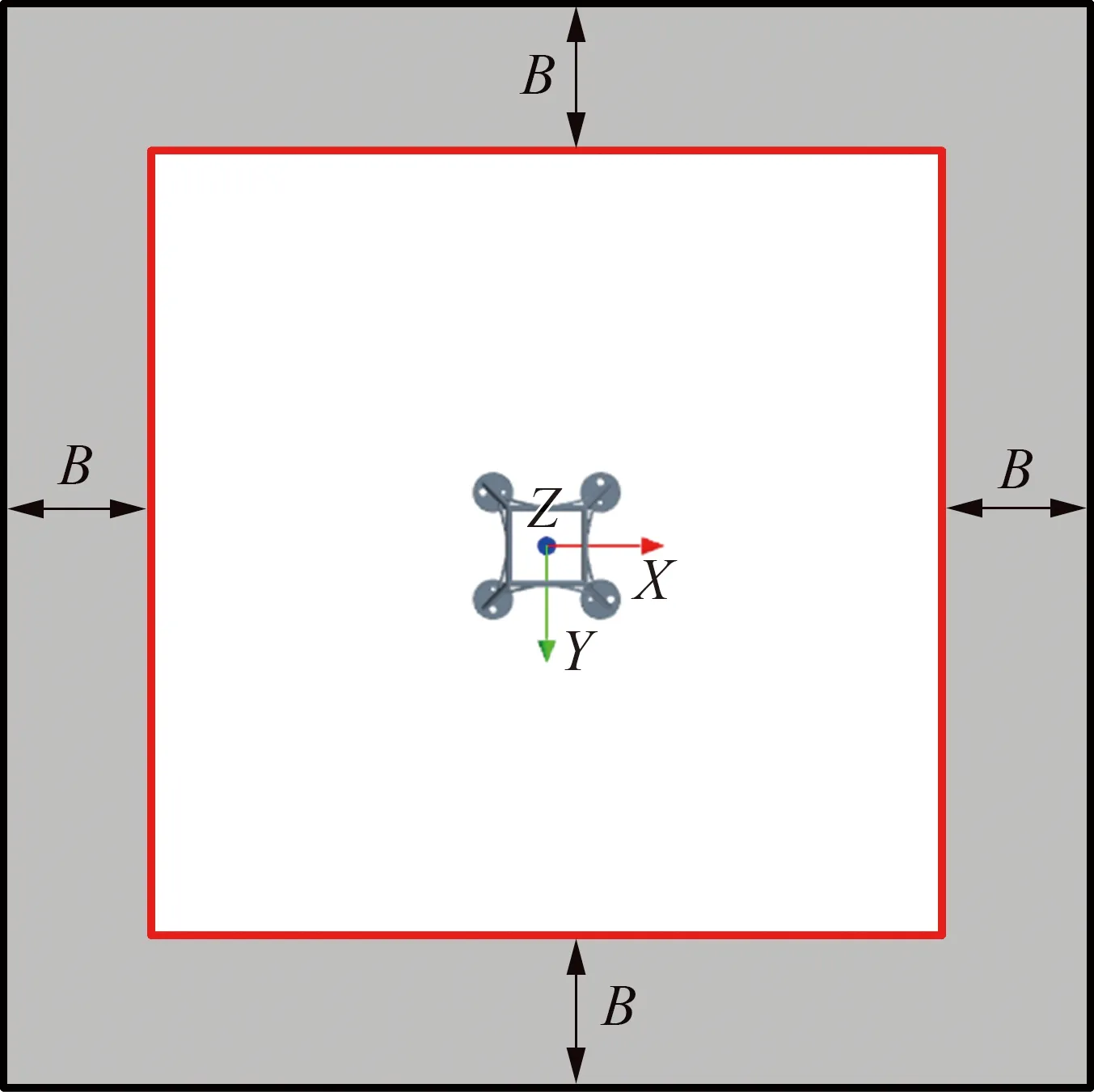
(a) (b)
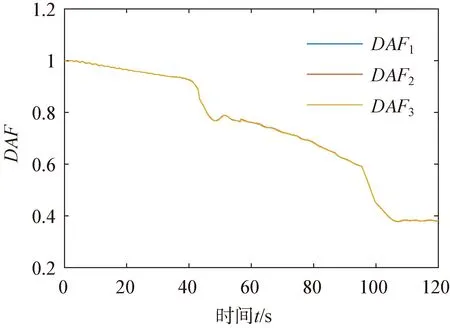
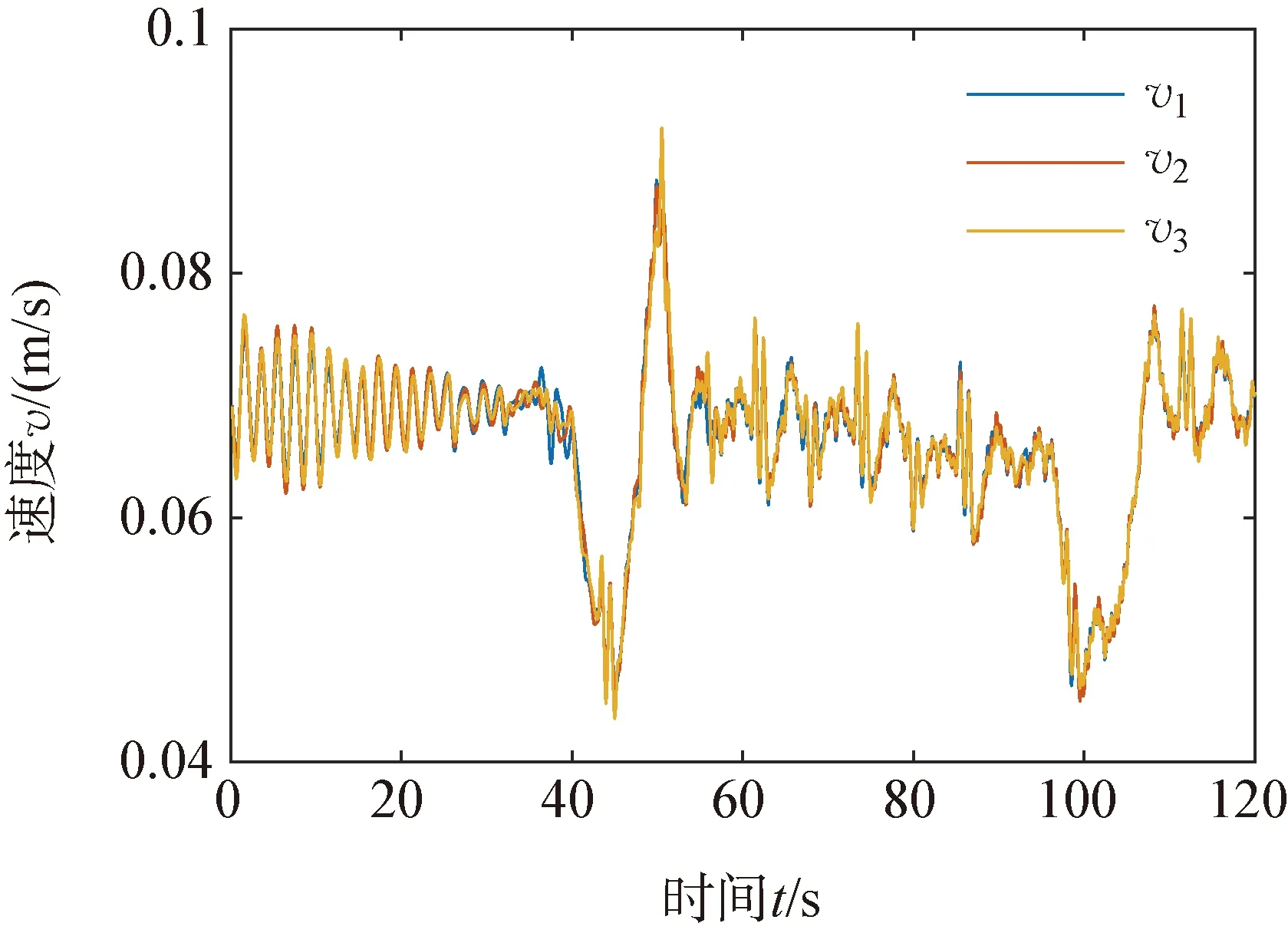
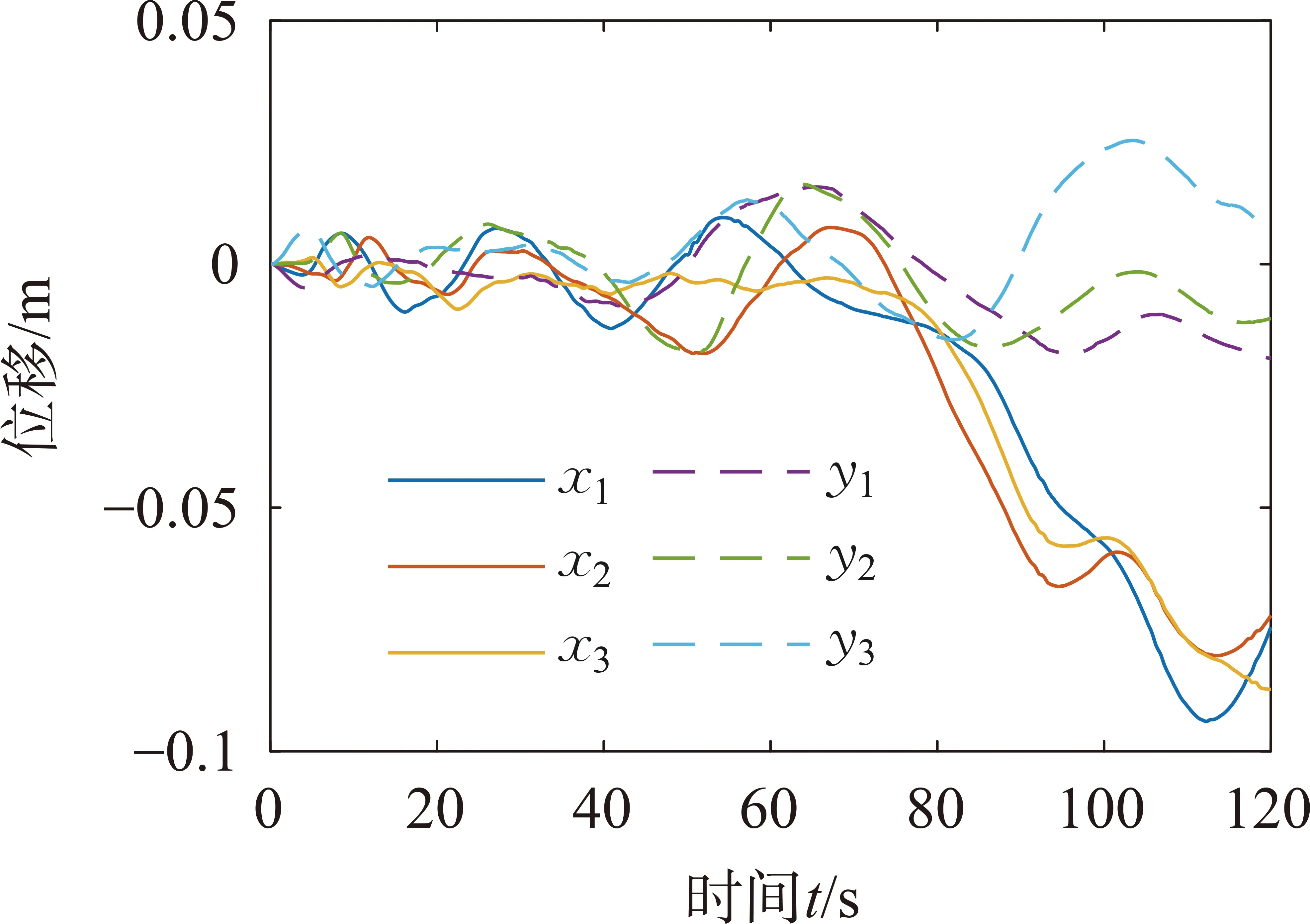
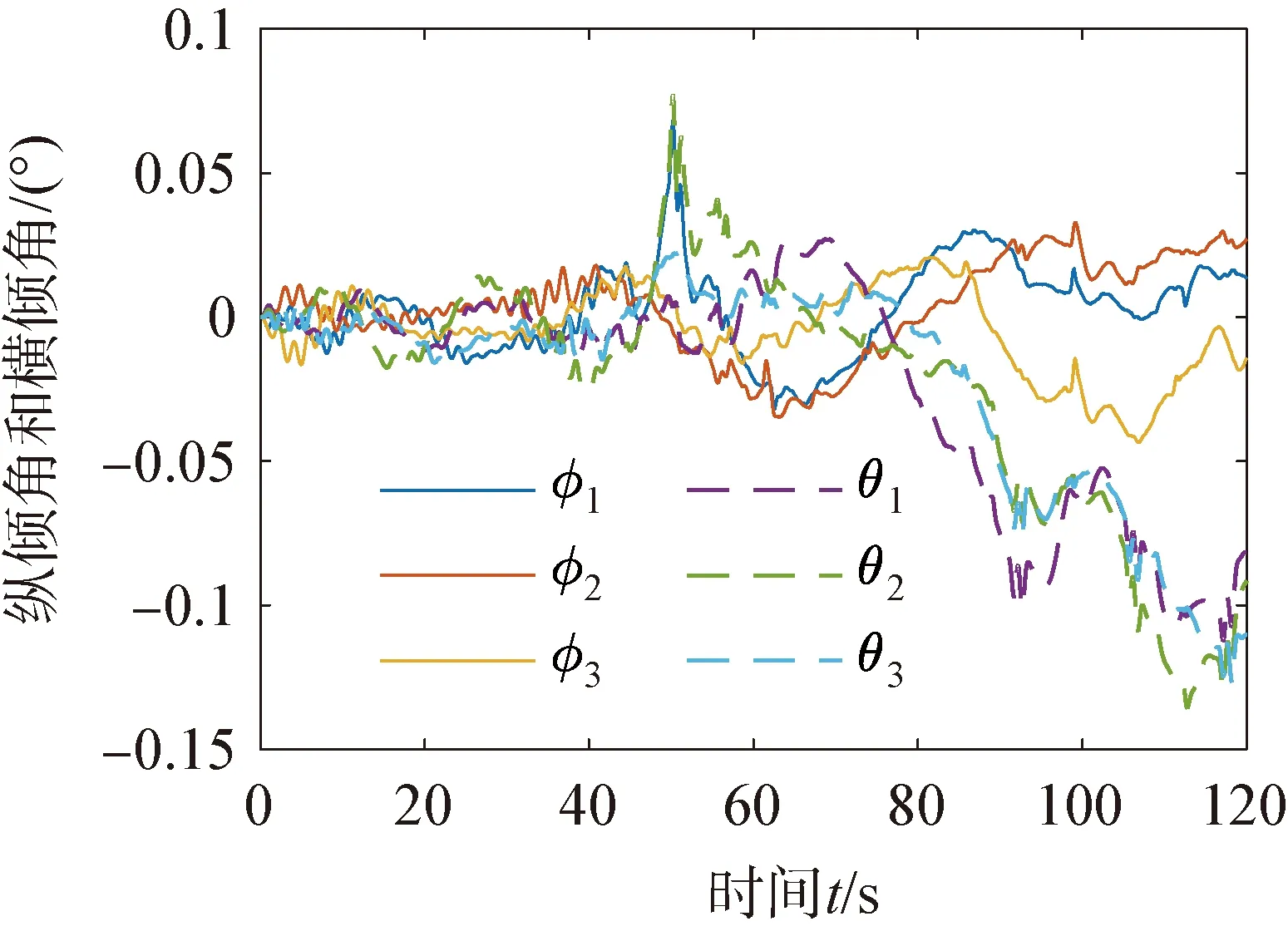
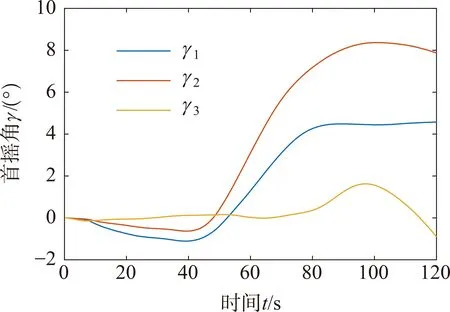
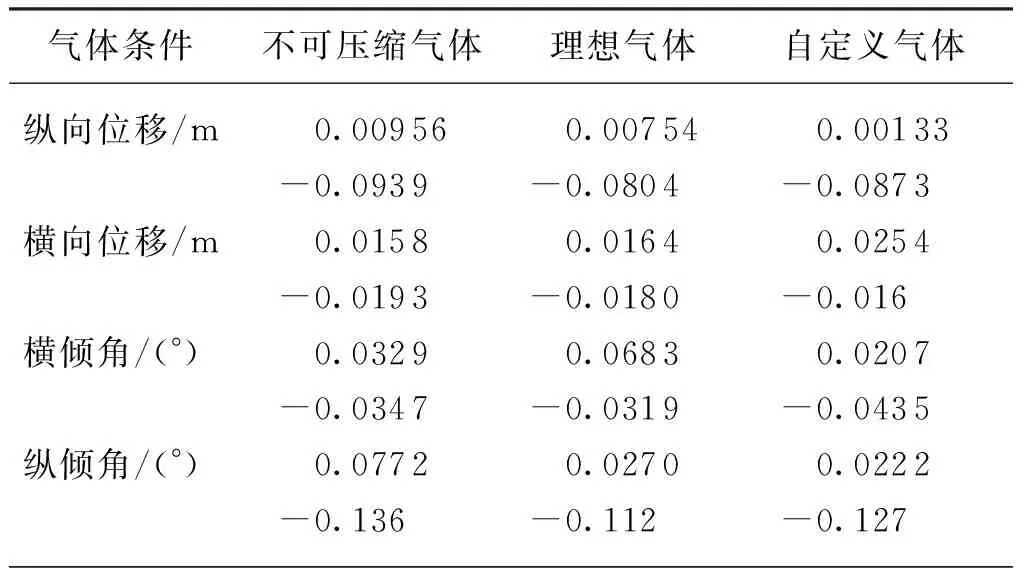
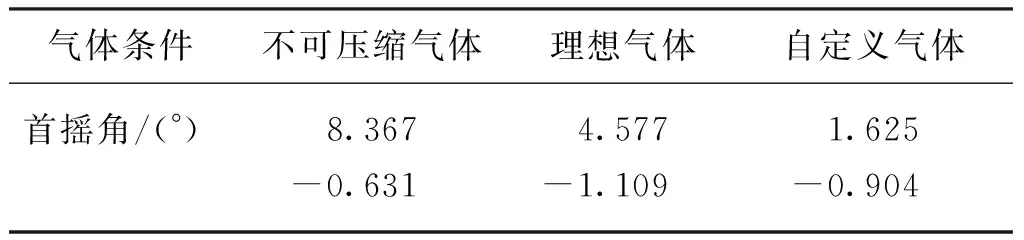
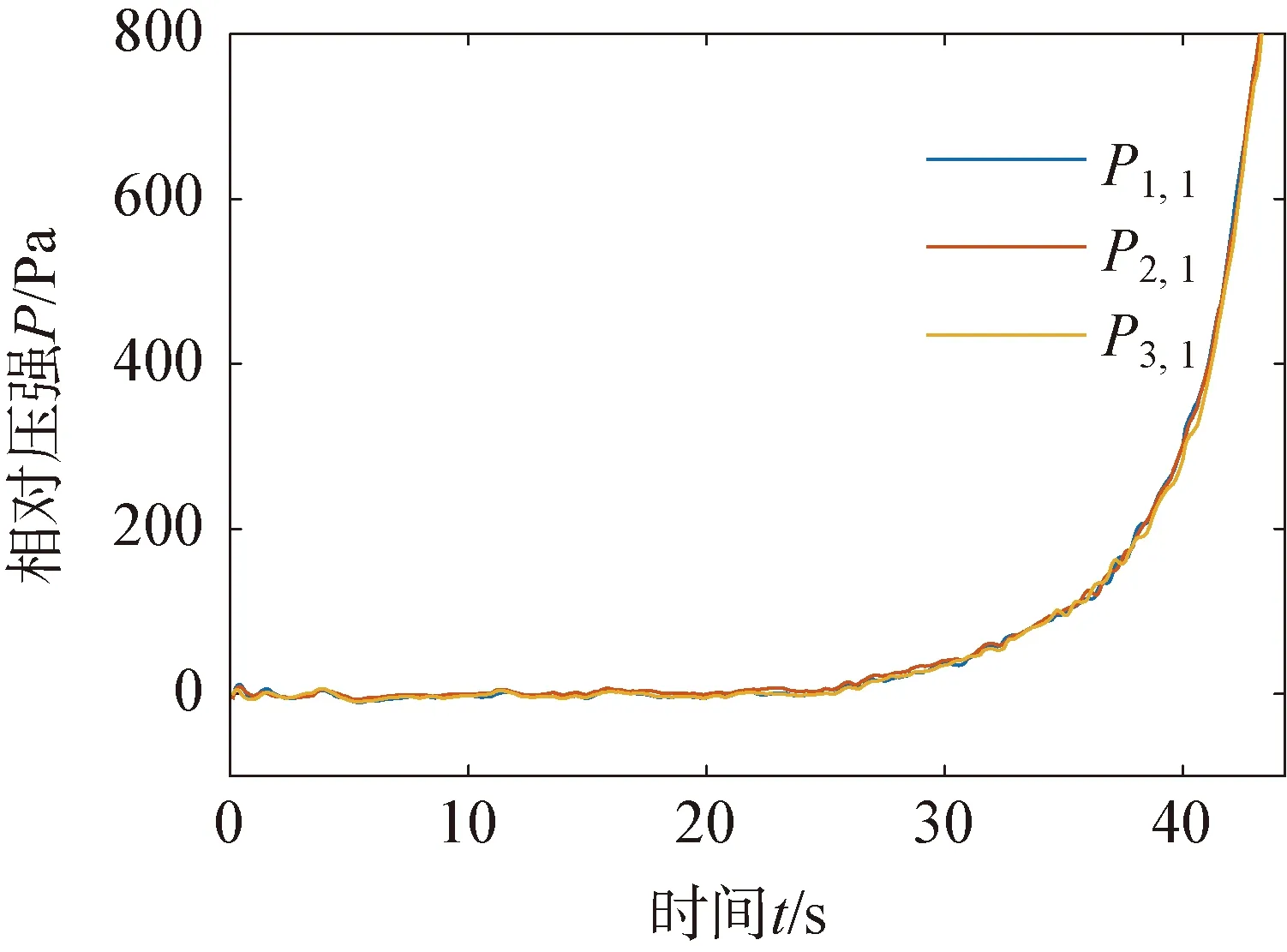
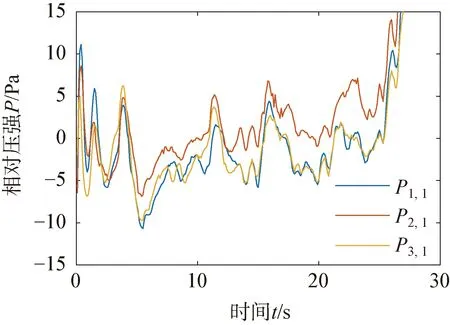
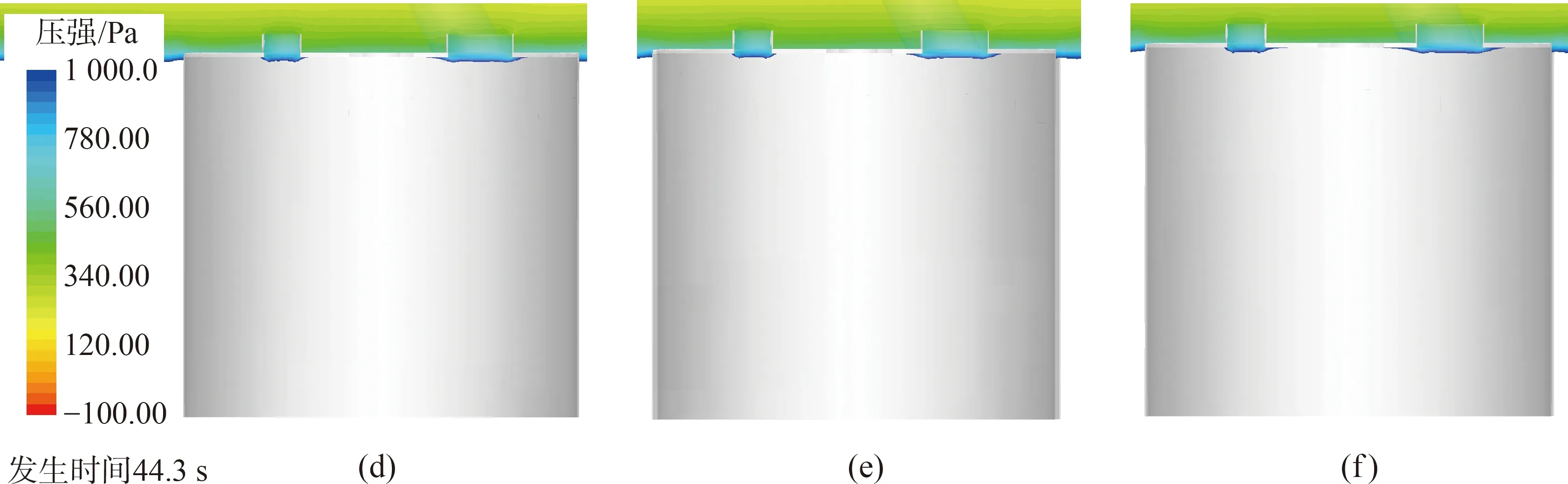
由初始化激活的動網格過度區域和自由液面的自適應網格(adaptive mesh refinement,AMR)如圖3(b)所示,網格基準值0.2 m,最小值0.012 5 m,兩層邊界層網格總厚度為0.07 m,變化率為1.5,y+=337.07,共計3 436 163個網格。應用雙層全y+壁面函數(two-layer ally+wall treatment),該方法可以處理y+小于1和大于30的情況,當1 (a) (b) (c) (d) 根據DNVGL規范[18]中的結構物穿過飛濺區受力的簡化方法計算吸力錨錨頂觸水時纜繩拉力,并與計算結果中的同時刻的拉力進行比較以驗證方法的可靠性。錨頂的特征砰擊力Fslam,i可取為(i=1,2,3) (8) 其中,一個吸力錨的水平投影面積As=6.792 m2,砰擊力系數Cs=2π。砰擊速度vs, i從計算的位移實例中獲取,不可壓縮、理想氣體和自定義氣體條件下的砰擊速度:vs, 3=0.067 6 m/s,vs, 2=0.078 0 m/s和vs, 1=0.067 0 m/s。吸力錨錨頂觸水時一個吸力錨的瞬時浮力Fρ, i=76.244 m3,瞬時浮力根據不同吃水時的結構物瞬時浸沒體積計算。由于纜繩頂端固定且自由液面為靜水,作用在物體上的特征質量力FM,i可取為 FM,i=(ρVi+A33i)·a (9) 式中:Vi為吸力錨的瞬時浸沒體積;a為結構物的加速度;A33i為垂向附加適量,其估算方法為 (10) 其中,h為吸力錨的高度,與錨頂等面積的圓形平板的法向附加質量A33o=9 kg。一個吸力錨的拖曳力FDi為 (11) 其中,流速vr,i=vs, i。因為當不考慮水流或下降速度引起的尾波沖刷時,可以得到拖曳力系數在4~8范圍內,所以取拖曳力系數CD=8[18]。一個吸力錨的特征水動力Fhyd, i為 (12) 所以纜繩的拉力Ti: Ti=Mg-4(Fhyd, i+Fρ, i) (13) 其中,M為結構物的質量;g為重力加速度。計算結果如下:T1=222 323.062 N,T2=217 980.202 N,T3=222 561.815 N。模擬結果與簡化方法的計算結果之間的相對誤差均小于8%,所以本研究中的物理模型、參數和網格適用于靜水面的吊裝作業模擬。 本文利用線性彈簧模擬吊繩,進行吸力錨的飛濺區單吊作業仿真,參考DNVGL規范[18],動態放大系數(DAF)定義如下: (14) 式中:Fstatic為靜態載荷,包括吸力錨的重力和吊裝過程中各時刻吃水下的瞬時浮力,瞬時浮力根據不同吃水時的結構物瞬時浸沒體積計算;Ftotal表示靜態載荷與動態載荷之和,本文中表示纜繩拉力。 結構物在下放時,不可壓縮氣體(DAF1和v1)、理想氣體(DAF2和v2)和氣體比熱比為1.4的氣體(DAF3和v3)三個模型的DAF和結構物的垂向運動速度時歷如圖4所示。從圖4中可以看出,隨著結構物吃水、附加質量力和拖曳力增加纜繩拉力減小,并產生砰擊力;由于結構物從靜止突然運動,速度發生震蕩,但平均速度為0.07m/s,所以拉力和DAF呈線性變化;在錨頂觸水時,引起較大的浮力和附加質量變化,水下投影面積增加,拖曳力快速增大,DAF和結構物速度快速減小。 在錨頂沒入水中后,結構物加速下落,而且由于速度的突變,纜繩產生突變載荷,并影響后續下落過程的速度。根據DNVGL規范[18],突變載荷小于拉力的90%時,纜繩不會發生松弛。三種氣體條件下的突變載荷分別為Fsnap, 1=206 721.414 N、Fsnap, 2=206 580.239 N和Fsnap, 3=206 593.836 N,均小于重力的16%,所以纜繩并不會發生松弛。 由于錨頂入水后,結構物的拖曳力隨投影面積顯著增加,而且管架的形狀較吸力錨復雜,所以DAF大幅小于第一階段的幅值并繼續近似線性減小;最后,當管架頂端入水時,產生速度和載荷的突變,DAF在管架頂端入水后恒定。 三種氣體條件下的DAF曲線吻合得較好,三者的突變載荷和穩定的拉力相差小于1%,所以氣體的可壓縮條件對于開孔率為3.9%的吸力錨吊裝作業纜繩拉力影響較小。在錨頂觸水前,可壓縮性氣體下的速度振蕩幅值大于不可壓縮條件,在理想氣體條件下的速度振幅最大,最大振幅為0.008 m/s;理想氣體和自定義氣體條件下的速度與不可壓縮條件下的速度最大相對誤差分別為6.4%和10%,最大速度v1, max=0.087 64 m/s、v2, max=0.087 11 m/s和v3, max=0.091 89 m/s,最小速度v1, min=0.044 99 m/s、v2, min=0.044 98 m/s和v3, min=0.043 55 m/s。 (a) (b) 如圖5所示,三種空氣模型條件下吸力錨浸沒并產生拉力突變的時刻相差小于1%,全部結構物入水耗時的相對差值也小于1%。其中自定義氣體條件下吸力錨入水耗時最長,時長為45.03 s;理想氣體條件下全部結構物入水耗時最長,時長為103.33 s。當發生突變載荷時,吸力錨已經全部浸入水中并有大量的水從通氣孔中射出;發生突變載荷時仍有部分空氣從小尺寸的通氣口溢出,少部分殘留在錨頂下形成空腔,在大尺寸通氣孔周圍的空氣將被困于吸力錨內。 (a) (b) (c) (d) (e) (f) 圖6表示結構物的縱向(x)和橫向(y)的位移以及傾角,錨頂入水前結構物的位移、縱傾角(θ)和橫傾角(φ)發生對稱的振蕩,而且振幅和周期隨時間增加;當氣體為可壓縮時振蕩的峰值出現滯后,自定義的氣體條件下的縱向位移呈現非對稱變化且振幅較小;錨頂入水后,由于開孔的非對稱分布以及由鋼架產生的升力的作用,兩個方向的位移、縱傾角和橫傾角出現非對稱變化且出現最大值;理想氣體條件下,橫傾角和不可壓縮條件下的縱傾角出現較大的峰值;在錨頂入水前結構物發生小幅度的首搖,在錨頂入水后,當大量的水從通氣孔涌出時,由于其非對稱的分布,結構物發生大幅的向右舷的首搖;氣體為可壓縮條件時最大首搖角較小,而且自定義氣體條件的首搖角率先恢復為零,最大位移和歐拉角如表1所示。三種氣體條件下最大橫向位移0.025 4 m沿+Oy0方向,最大縱向位移-0.093 9 m沿-Ox0方向,均小于寬度的1%,不可壓縮條件下的縱向位移大于可壓縮氣體條件而橫向相反;最大橫傾角φ=0.068 3°,最大縱傾角θ=-0.136°,最大首搖角γ=8.367°。 (a) (b) (c) 表1 最大位移和最大傾角 (續 表) 如圖7所示,為吸力錨頂部下表面圓心處的相對大氣壓的相對壓強時歷。隨著結構物的吃水增加,吸力錨內部的相對壓強逐漸非線性增加。在開孔率為3.9%時,由于吸力錨內外的液面高度差小,吊裝速度緩慢,吸力錨內部的空氣壓縮不明顯,不同氣體條件對吸力錨內壓強的影響較小。在吸力錨穿過飛濺區的初期,內部相對壓強較小但存在較大振蕩,幅值最大超過10 Pa。如圖8所示,由于初期的垂向速度不穩定且液面存在擾動,相對壓強出現負值。與其他氣體條件相比,理想氣體條件下的正壓較大負壓較小。不同吸力錨內的壓強對比如圖7(c)和圖7(d)所示,在入水初期,4個吸力錨之間的差異較小,在錨頂接近水面時壓強的差異增加,3號吸力錨的壓強最大,4號吸力錨的壓強最小,吸力錨之間的壓強差值在錨頂觸水時最大為85.685 Pa,為該時刻4號吸力錨內壓強的15%。由于垂向速度較小且存在空氣的緩沖作用,錨頂觸水時壓強沒有明顯的突變峰值,說明在最大投影面積的位置,由水與結構物的突然接觸而產生的砰擊載荷較小。 (a) (b) (c) (d) 圖8 自由液面位置 如圖9所示,入水初期氣體可壓縮與不可壓縮條件的壓力分布差別較小,吸力錨內部的壓強分布從上到下逐漸增加,且高壓區域的分布梯度比外界大;當錨頂觸水時,在可壓縮氣體條件下,有更多的空氣留在通氣孔附近。 圖9 不可壓縮氣體、理想氣體和自定義氣體的壓強分布 本文采用計算流體力學方法對帶有四個吸力錨的結構物進行飛濺區單吊作業時纜繩拉力、運動狀態和吸力錨內部壓強進行分析,分別研究空氣為不可壓縮條件、理想氣體條件和比熱比為1.4的自定義氣體條件對吊裝作業的影響。 結果表明當以全局力為研究重點,在較低速的不會產生纜繩松弛的吊裝作業中,為簡化計算可視空氣為不可壓縮氣體,但此時對結構物運動狀態的估計是保守的;在靜水可壓縮空氣條件下,不同吸力錨由于相對液面運動狀態不同,造成水動力以及內部壓強的差別較小,所以可進行對稱簡化。比熱比的變化對橫向和縱向位移影響較小,但在吸力錨入水初期,比熱比增加時,位移的振蕩周期增加峰值減小,吸力錨完全入水后較大比熱比時的首搖角明顯減小,大比熱比時吸力錨頂部下方的相對壓強較小。本文針對帶有吸力錨的結構物,計算所獲得的載荷結果、運動和壓強的變化規律,可以為將來吸力錨的設計與安裝提供指導。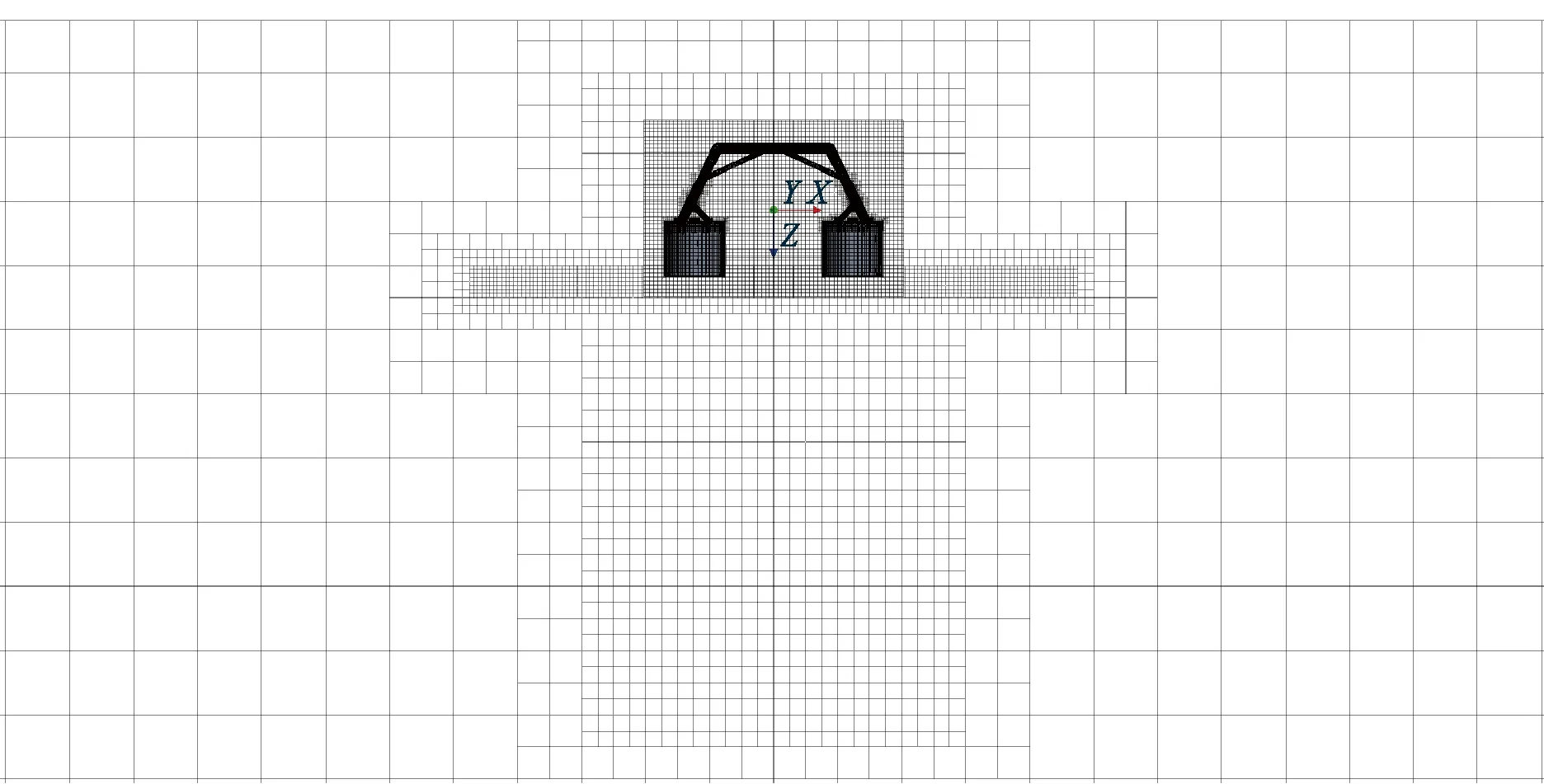


2 仿真結果驗證
3 計算結果與分析
3.1 纜繩拉力與吸力錨運動狀態





3.2 吸力錨內壓強分布
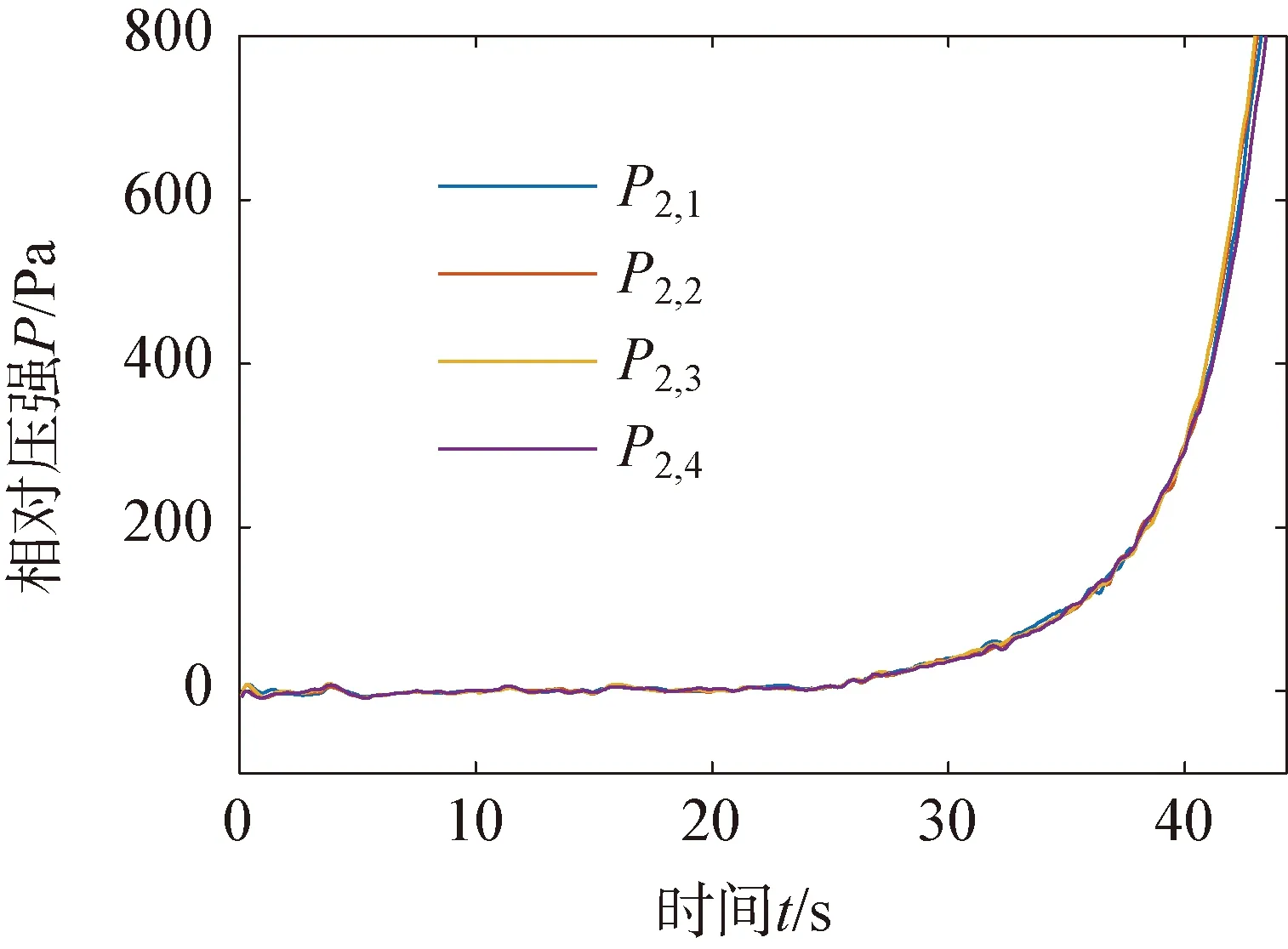
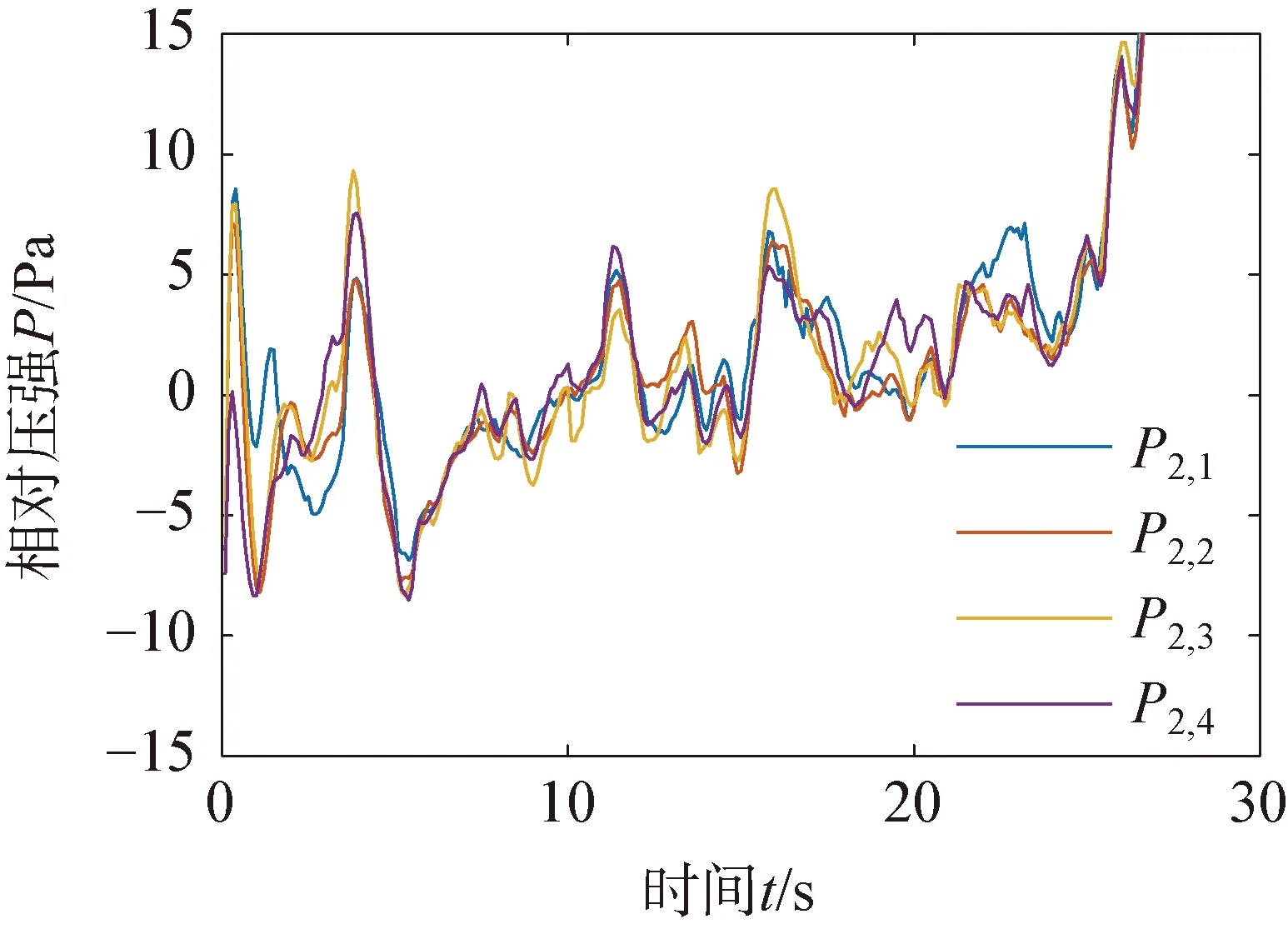
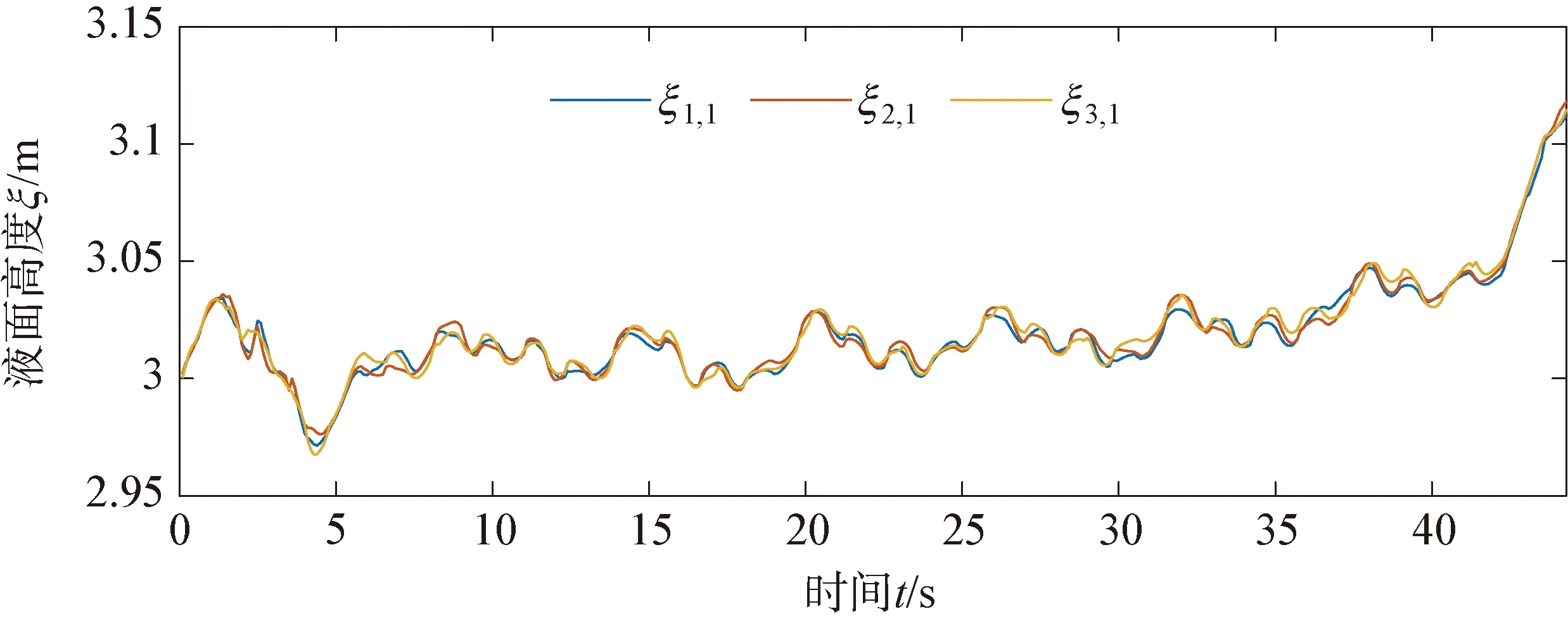
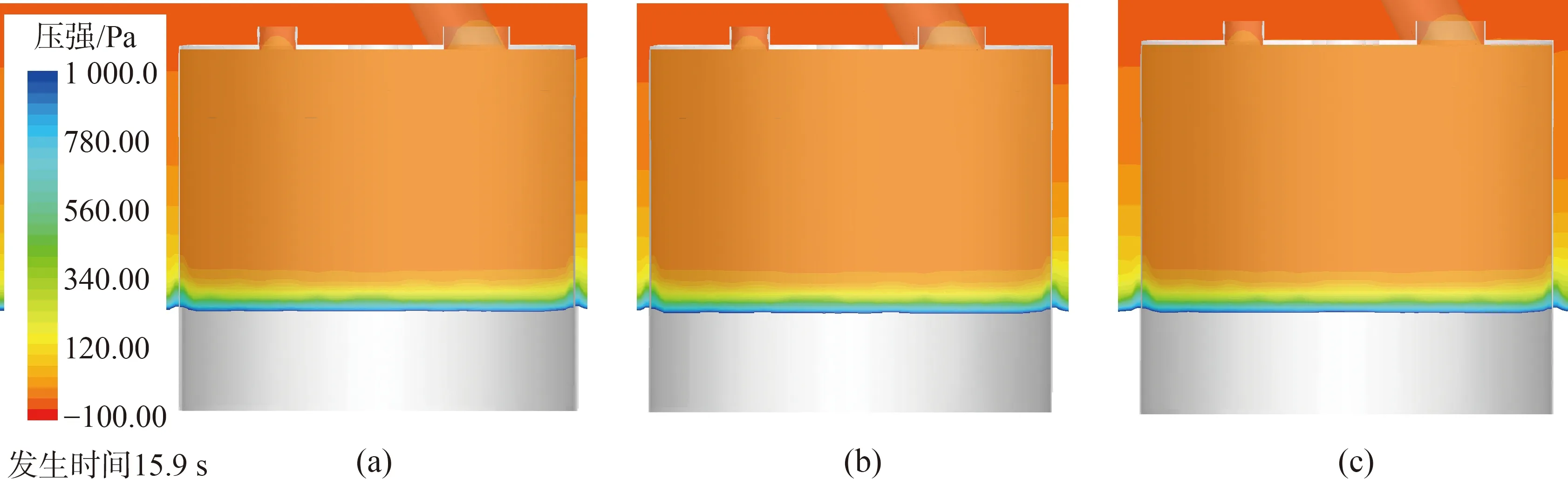
4 結 語

