淺水浮式風機動態電纜線型設計

蒲 定，楊婉秋，豐如男，俞國軍，楊 帆，陳仁棟，宋幼忠，張治安

(1. 中海石油(中國)有限公司深圳分公司，廣東 518052；2. 寧波東方電纜股份有限公司，寧波 315000)

0 引 言

隨著海上風電開發由淺水向深遠海發展，浮式風電系統的應用已成為必然趨勢。目前世界各地已部署了大量的浮式風機樣機。風機主要采用三葉片形式，浮式平臺的類型主要包括Spar、駁船和半潛式平臺等[1]。全球主要的風機市場包括歐洲、日本和美國西海岸。預計歐洲、美國和日本的浮式風機潛在裝機容量約為7 GW。Hywind Consortium指出，日本(3.5 GW)、法國(2.9 GW)、美國(2 GW)和愛爾蘭/英國(1.9 GW)是一個潛在的市場，在2030年之前有大量的部署機會[2]。

動態電纜是浮式裝置的關鍵部件之一。從浮式平臺到海床，通常連接到靜態海底陣列/輸出電力電纜。這些電纜必須保持盡可能高的完整性，以確保不間斷發電。我國海域近岸水深變化小，水深普遍不超過60 m[3]，同時浮式風機所處海域通常環境非常惡劣，風機系統會在風、浪、流的加載下發生非常大的偏移。

目前有很多學者針對淺水的動態電纜/立管進行研究，但案例中偏移量大多只有水深的一半[4-5]，同時國內淺水浮式風機動態電纜在工程上尚無實際應用案例，不同方案的優劣尚未得到充分研究。為此，本文將針對不同動態電纜線型進行分析，提出適用于淺水浮式風機動態電纜的一種線型方案。

1 系統參數

1.1 環境參數

南海路由區平均水深為30 m。 50年一遇有效波高為10.55 m，譜峰周期為14.1 s，一年一遇波浪有效波高為5.5 m，譜峰周期為11.2 s。 50年一遇最大流速為1.43 m/s，一年一遇最大流速為0.7 m/s。路由區土壤類型為淤泥質粉質黏土，不固結不排水剪切黏聚力為18.2 kPa。洋流參數如表1所示。

表1 洋流參數

1.2 整體構型

目標風機為單機功率5.5 MW的三葉片風機，風機基礎采用半潛式平臺結構，采用6點系泊。作為回路末端風電機組，采用1回路35 kV動態電纜與鄰近機位的固定風機組連接。整個動態電纜系統如圖1所示，動態段從半潛式平臺(右側)連接至一固定式風機(左側)。動態電纜系統參數如表2所示。平臺偏移量如表3所示，由表3可知，該浮式風機偏移量已大于水深，環境非常惡劣。

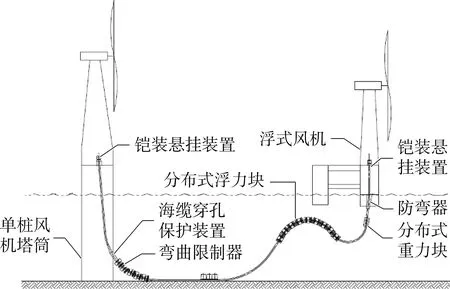
圖1 動態纜系統

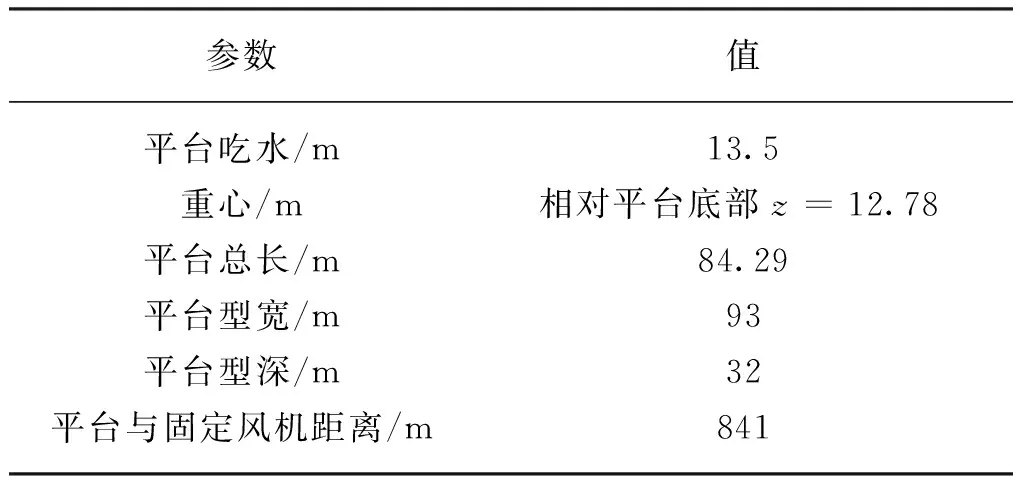
表2 動態電纜系統參數

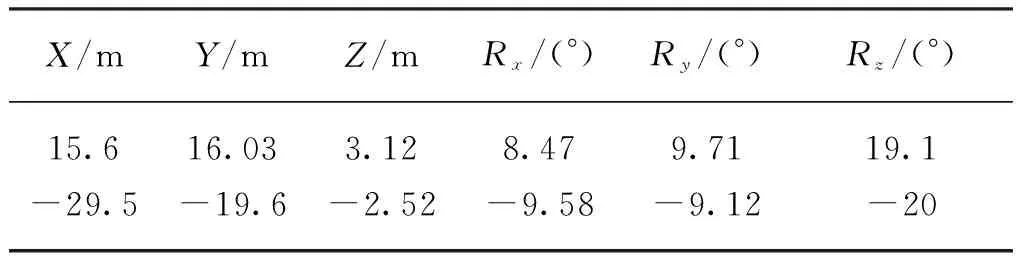
表3 平臺偏移量

1.3 動態電纜截面參數

動態電纜截面設計參數如表4所示。

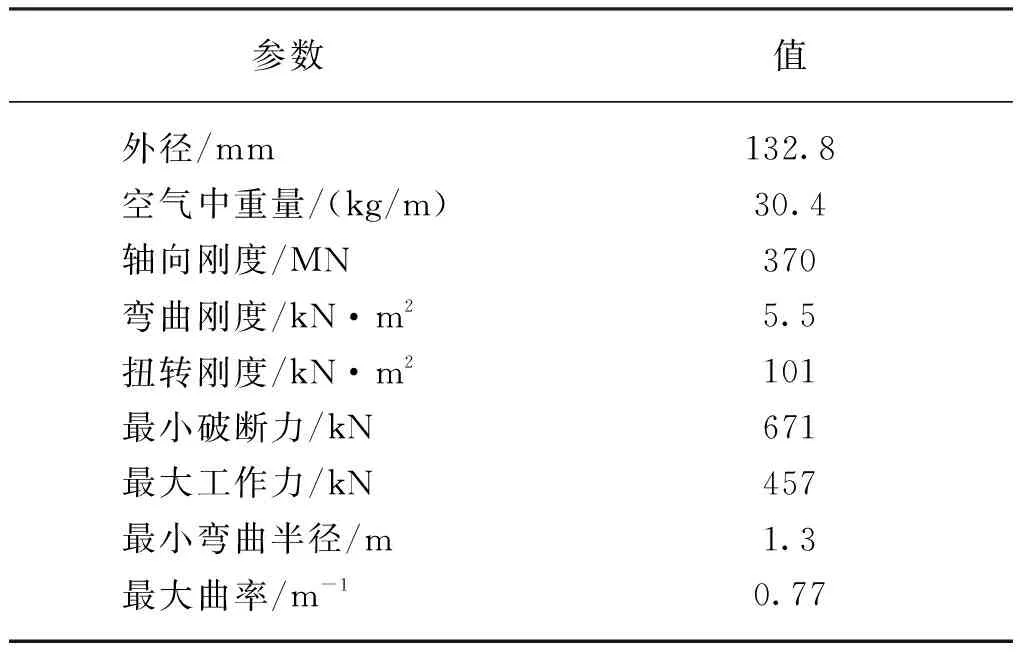
表4 動態電纜截面設計參數

2 線型設計

線型設計通過專業水動力分析軟件OrcaFlex[6]進行。OrcaFlex中采用集中質量法對線單元進行離散，將動態纜的連續質量在空間內離散到有限節點上，節點之間采用拉伸、扭轉、彎曲彈簧和相應阻尼器進行連接，以表現動態纜線單元的拉伸、扭轉、彎曲特性。集中質量模型如圖2所示。

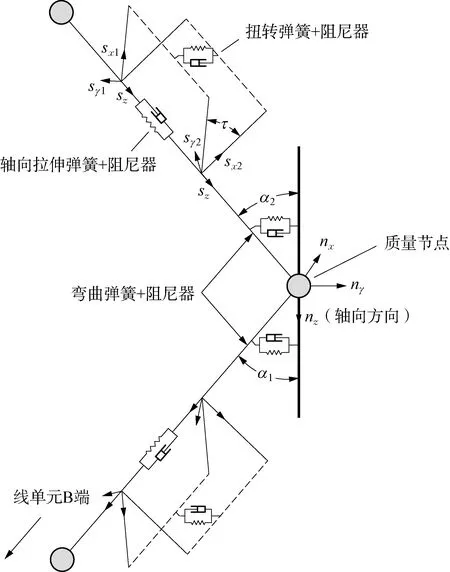
圖2 集中質量模型

動態纜滿足運動方程：

M(p，a)+C(p，v)+K(p)=F(p，v，t)

式中：M(p,a)為系統慣性載荷；C(p,v)為阻尼載荷；K(p)為剛度載荷；F(p,v,t)為外部載荷；p、a、v、t分別為位置、加速度、速度和模擬時間。

在OrcaFlex中，浮體運動以及波浪傳播可使用“time history”功能進行輸入，即將浮體每個時刻六自由度位置和波浪在每個時刻的波面升高數據作為線型設計的輸入參數。離散的浮體運動數據將通過三次樣條插值恢復為連續的浮體運動，離散的波高數據則通過FFT方法重新離散為若干不同頻率的規則波分量。

由于動態電纜多在水面以下的環境中，可忽略風的影響，僅考慮波浪、洋流以及上部浮體的運動。波浪和浮體的運動采用時歷方法進行輸入。首先對不同風機朝向、不同風向和波浪方向的整個浮體(風機+浮體)運動進行模擬，其中波浪采用不規則波(Jonswap譜)模擬50年一遇波浪。輸出每個工況下整個浮體的運動時歷和波浪的波高時程，共計12組組合工況。洋流采用50年一遇流速，方向與波浪方向一致[7]。

環境參數確定后，須對基礎線型進行選擇。常見線型有懸鏈線線型、緩波形線型、緩S形線型[8]，如圖3～圖5所示。

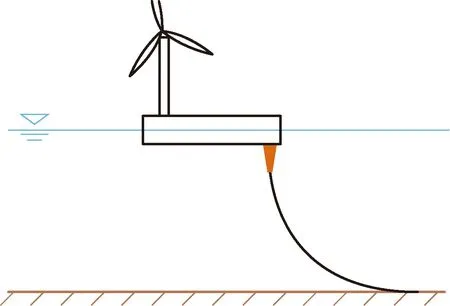
圖3 懸鏈線線型

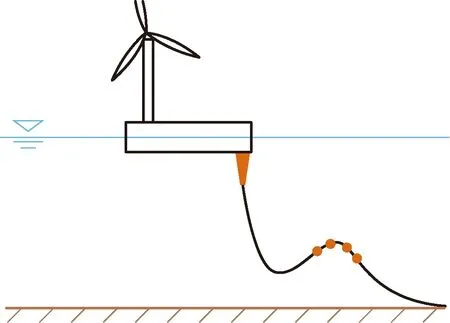
圖4 緩波形線型

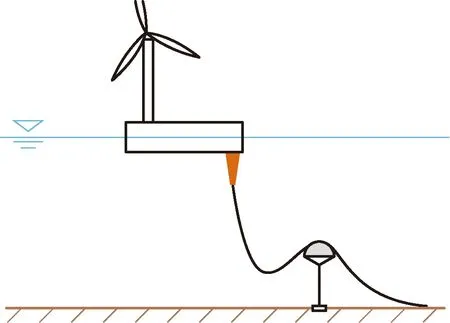
圖5 緩S形線型

波形線型是在懸鏈線基礎上增加分布式浮力塊，使動態電纜呈現出類似一個周期波浪的形狀，該形態相較懸鏈線型，對觸地點有一定程度的保護作用，比S形線型經濟。相較而言，波形較為適合浮式風機。確定基礎線型后，須對線型進行優化，使動態纜的力學性能在極值工況下仍能滿足要求。

3 極值分析結果

3.1 基礎型緩波線型

采用防彎器和分布式浮塊的基礎型緩波線型的12組工況極值分析結果如下，基礎型緩波線型如圖6所示。其中防彎器長度為4 m，浮塊采用0.1 t×8個，始于纜長27 m處，以1 m間距安裝。關于浮塊的選取，目前已有大量研究[9-13]，本文不再贅述。

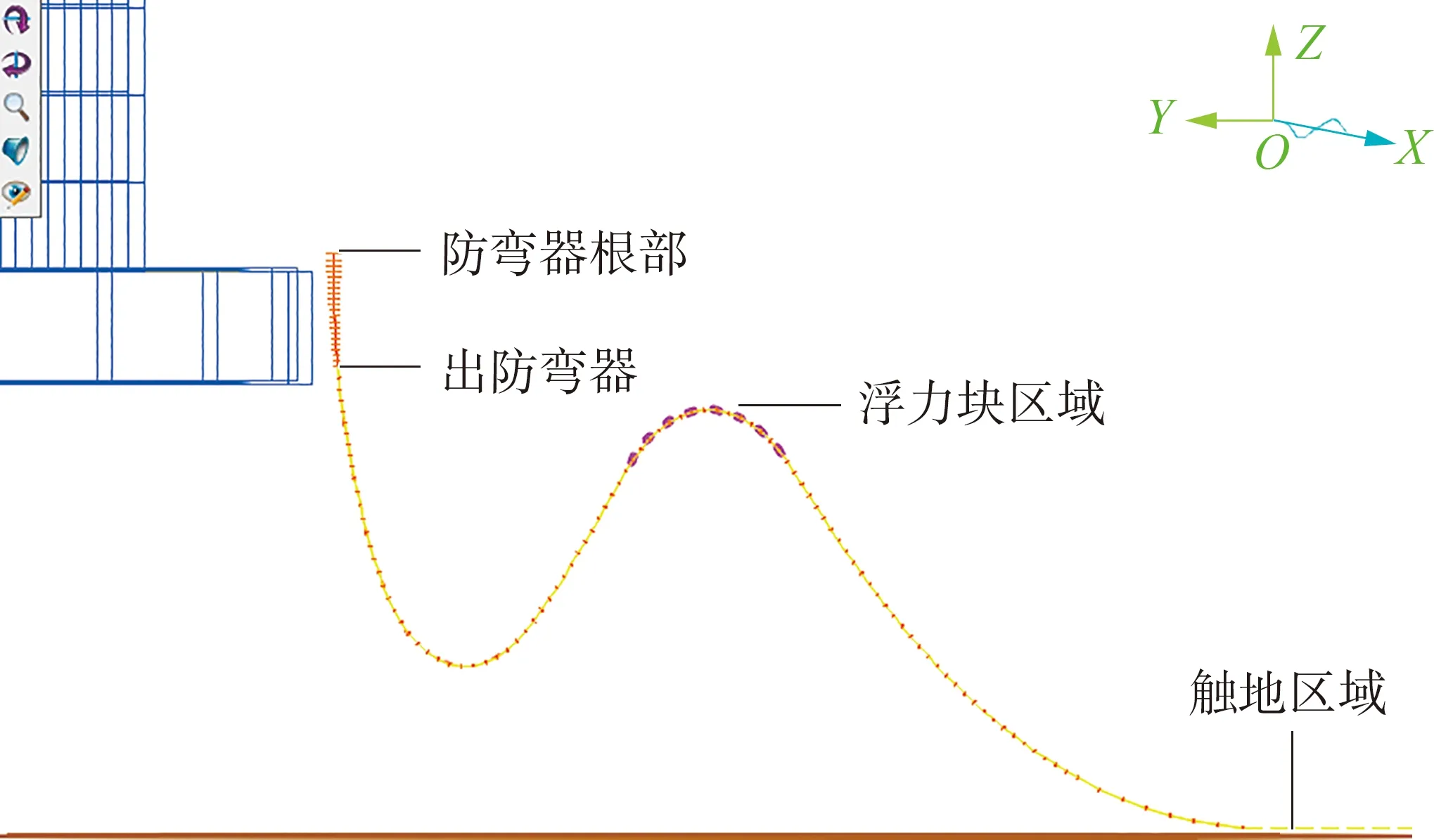
圖6 基礎型緩波線型

由表5結果可知，基礎型緩波線型在12組極值工況中最大張力都出現在出防彎器處，均可滿足許用張力457 kN的要求，但最大曲率結果僅為1.15～1.45 m-1，無法滿足許用最大曲率0.77 m-1的要求，工況1和工況10最大曲率出現在防彎器根部，表明這兩種工況下防彎器強度不夠，但其他10組工況最大曲率均出現在出防彎器的部分，說明這10組工況下防彎器強度足夠，但出防彎器后的纜橫向位移過大。針對上述情況，本文將采用在防彎器后加重塊的方式進行線型優化研究。

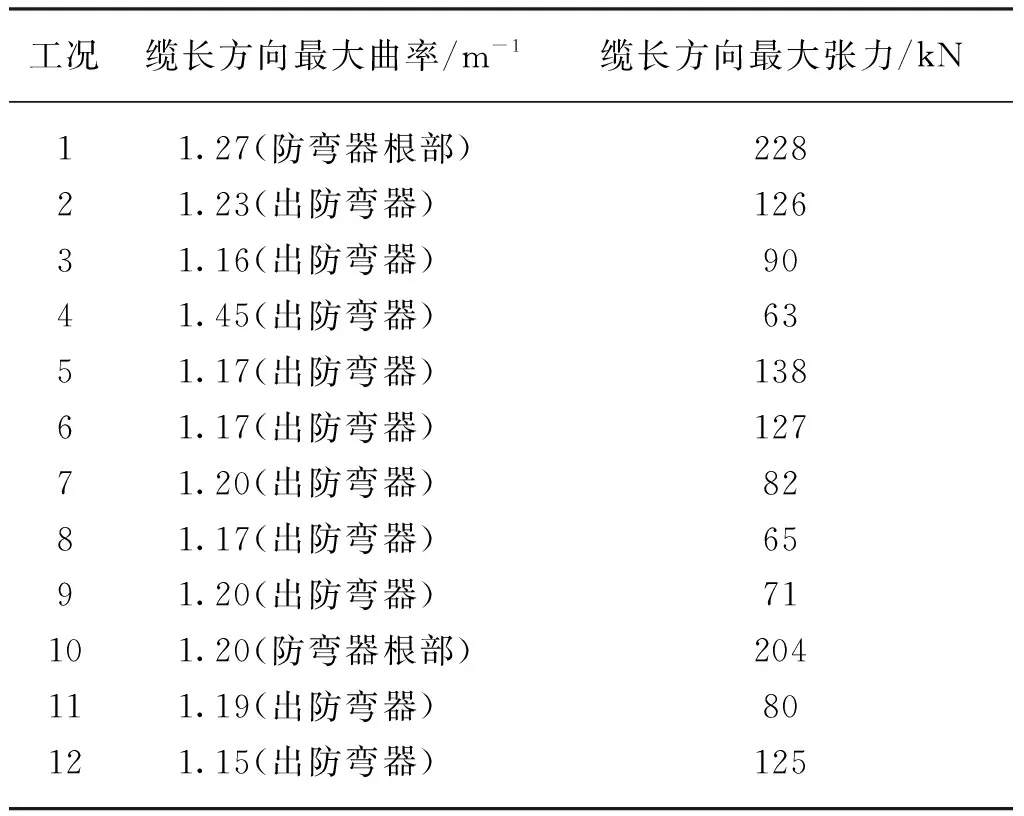
表5 基礎型緩波線型極值分析結果

3.2 加重塊型緩波線型

使用OrcaFlex中的attachment-clump模塊進行重塊的添加(見圖7)。以最危險的工況1(張力最大)和工況4(曲率最大)為基礎，首先對所加重塊的重量進行敏感性分析，在其他參數不變的條件下，分別采用重塊0.1 t×7個、0.2 t×7個、0.3 t×7個、0.4 t×7個四種方案，重塊間距為2 m，計算動態纜的動態響應。圖8～圖11為不同重量重塊在極值工況下沿纜長方向的張力分布和曲率分布。為了清楚顯示，曲率橫坐標僅給到80 m。

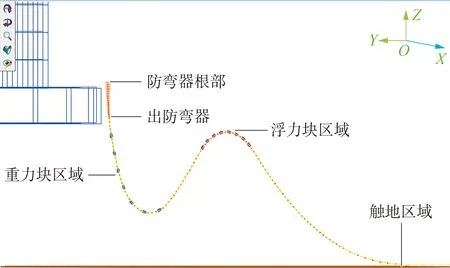
圖7 添加重塊的緩波線型示意圖

由圖8～圖11可知，動態纜在出防彎器時，有效張力突變至最大張力，曲率也有一個突變。在出防彎器之后添加重塊段，重量增加后纜的穩定性增大，偏移量隨即減小，出防彎器位置的張力和曲率均得到改善，并且改善隨著重塊重量的增大而增加。但隨著重塊重量的增加，出重塊段后的曲率突變也明顯隨之增加，張力則變化不明顯。由于動態纜的海底端設置為固定點，當波浪和流從動態纜側向入射時，海底部分會產生較大偏移，導致固定端位置張力較大，該情況可通過海底固定裝置改善，本文暫不做研究。在重塊重量敏感性分析中，有效張力均滿足許用張力要求，最大張力出現在0.2 t×7方案海底固定位置。在這兩種工況中，0.1 t×7方案的最大曲率均不滿足0.77 m-1的要求。工況1中0.4 t×7方案重量過大，出重塊處曲率超過許用最大曲率。只有0.2 t×7和0.3 t×7兩種方案在兩種工況下均滿足要求，考慮到經濟性，選擇0.2 t×7方案更佳。

圖8 沿纜長方向的張力分布(工況1)

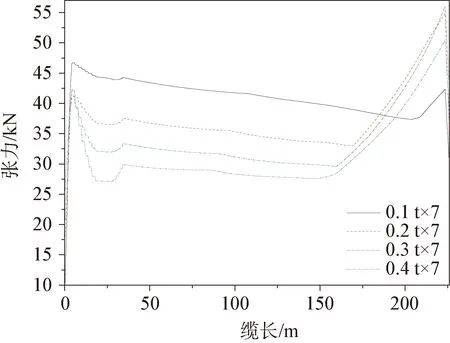
圖9 沿纜長方向的張力分布(工況2)

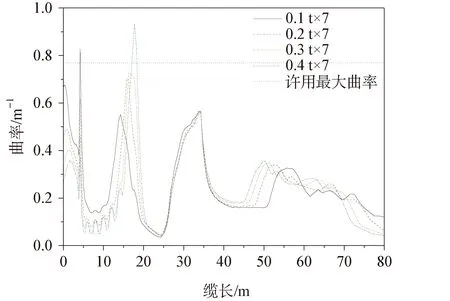
圖10 沿纜長方向的曲率分布(工況1)

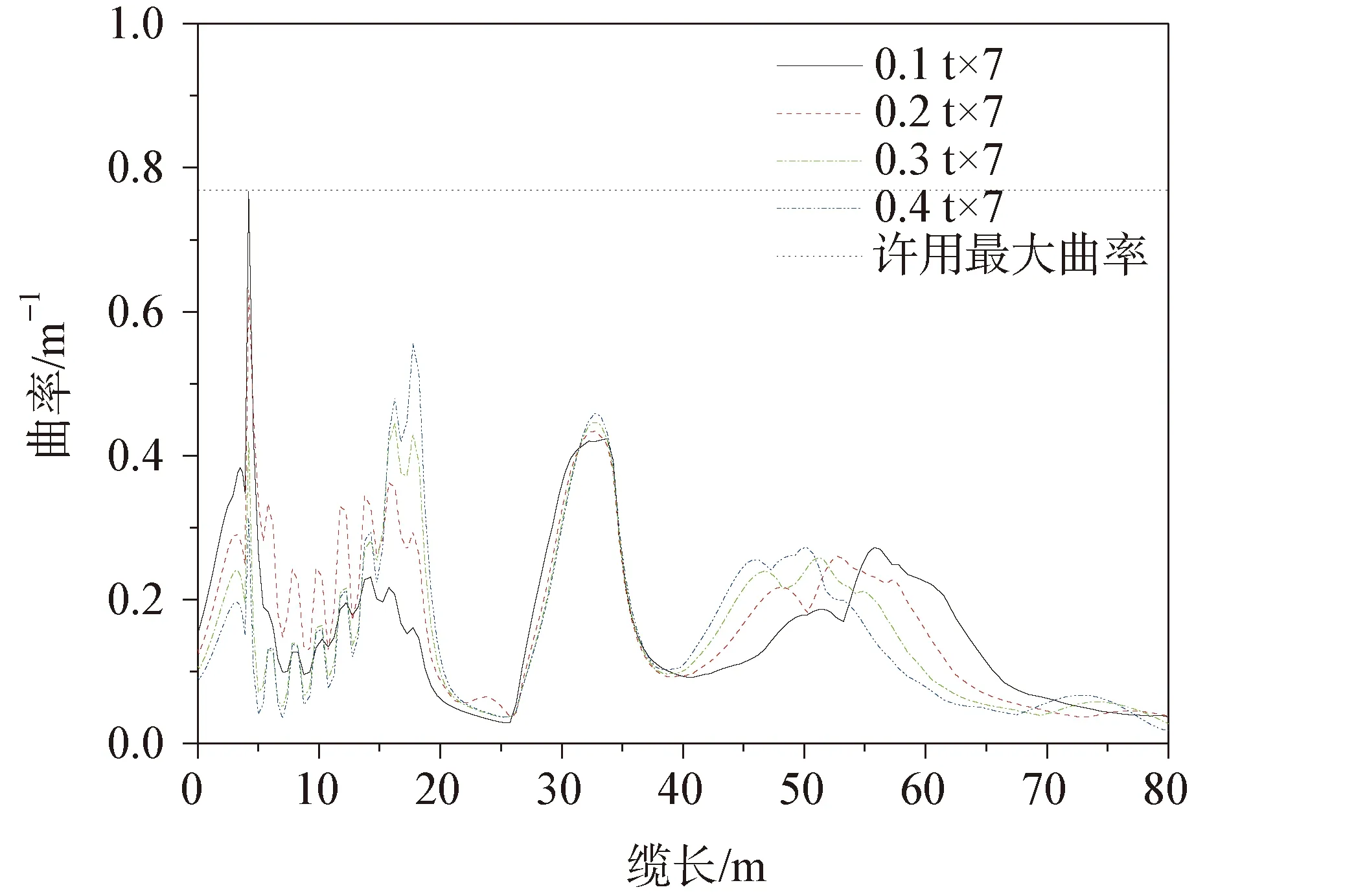
圖11 沿纜長方向的曲率分布(工況2)

大致確定重塊的重量后，須對重塊個數進行敏感性分析，將7個0.2 t重塊減少為6個、5個。動態分析結果如圖12～圖15所示。

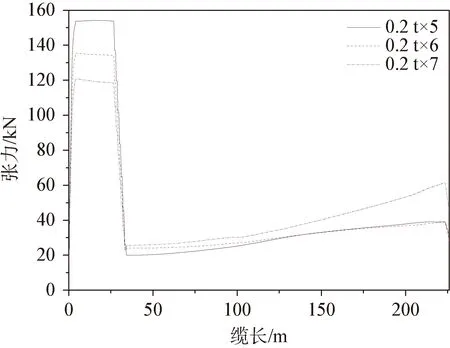
圖12 沿纜長方向的張力分布(工況1)

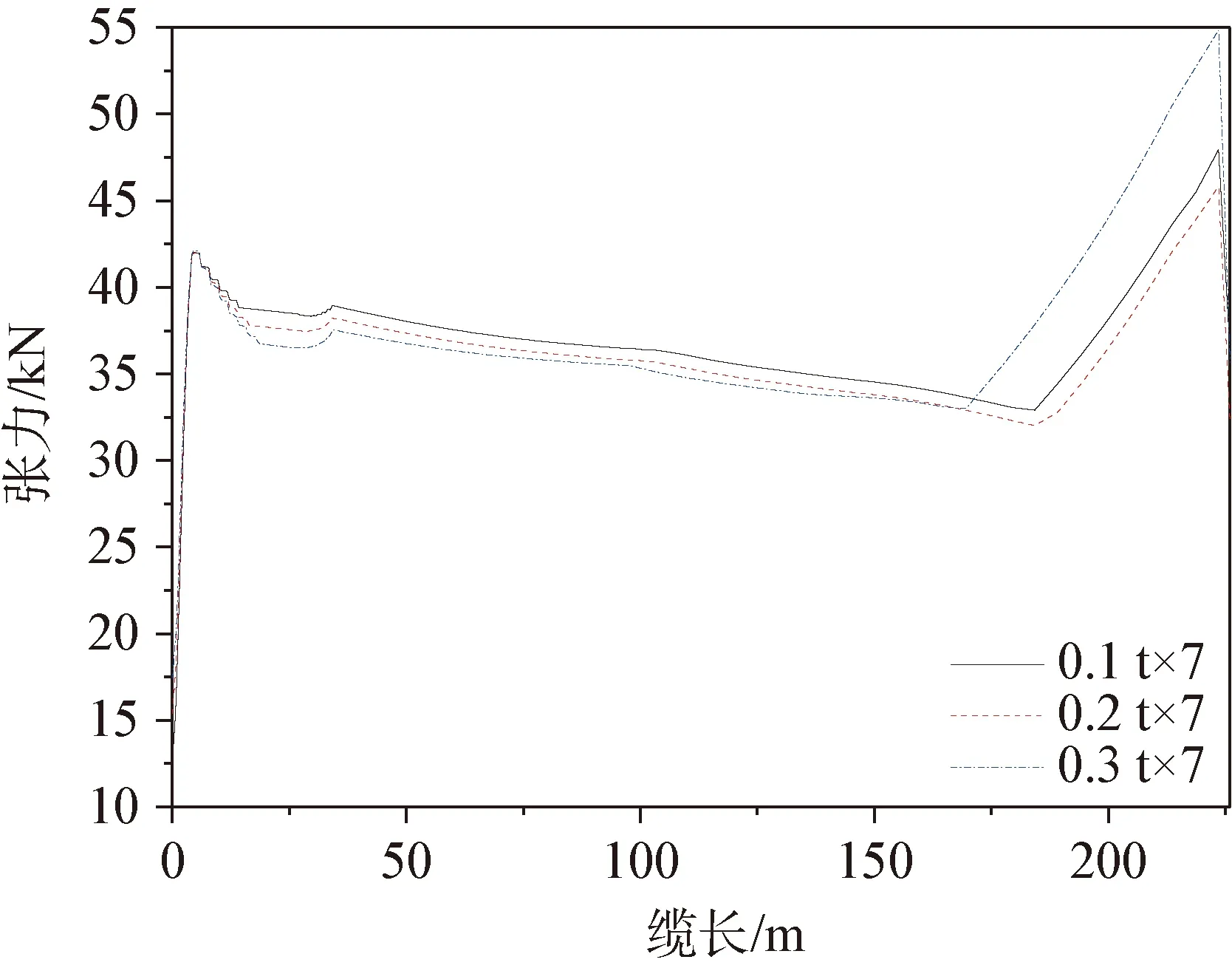
圖13 沿纜長方向的張力分布(工況2)

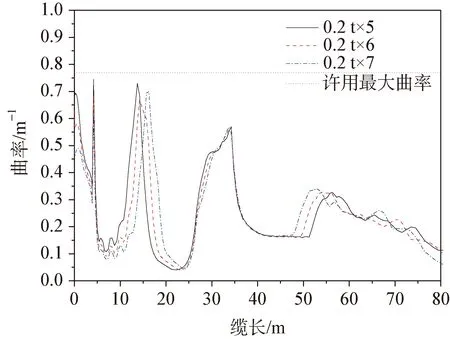
圖14 沿纜長方向的曲率分布(工況1)

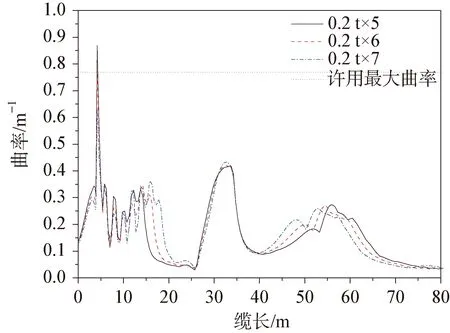
圖15 沿纜長方向的曲率分布(工況2)

由圖12～圖15可知，出防彎器區域，張力和曲率均隨著重塊個數減小而增大；出重塊段區域，工況1中曲率隨著重塊個數減少出現先減小后增大的趨勢，工況2則隨著重塊個數減少變化不明顯，說明重塊個數對出防彎器位置影響較大。兩種工況最大張力均能滿足要求，最大張力出現在0.2 t×7方案海底固定位置。重塊為0.2 t×5個時，最大曲率均小于許用最大曲率；重塊為0.2 t×6個時，工況2出防彎器位置最大曲率未滿足要求；0.2 t×7方案在兩個工況結果下均能滿足最大曲率要求，故選擇0.2 t×7個的方案。

然后對0.2t×7方案的重塊間距進行敏感性分析，分別采用1.5 m、 2 m、 2.5 m、 3 m的間隔均勻分布重塊。動態響應結果如圖16～圖19。結果顯示兩種工況最大有效張力均能滿足要求，出防彎器位置最大張力在工況1中與重塊間隔變化呈現1.5 m>2.5 m>2 m>3 m非線性關系，出重塊位置曲率隨著間隔增大而減小；工況2中張力則隨著間隔增大而增大，曲率則1.5 m>2.5 m>2 m>3 m，表明重塊間隔對張力的影響還與具體工況相關(波浪方向不同)。間隔為3 m時，兩種工況的最大曲率最小。

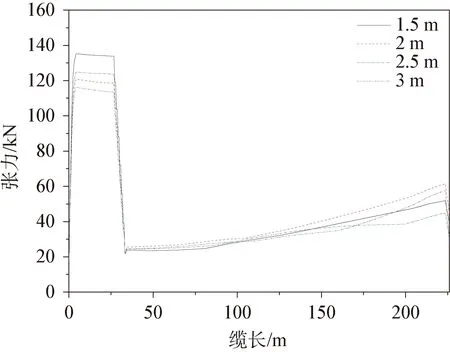
圖16 沿纜長方向的張力分布(工況1)

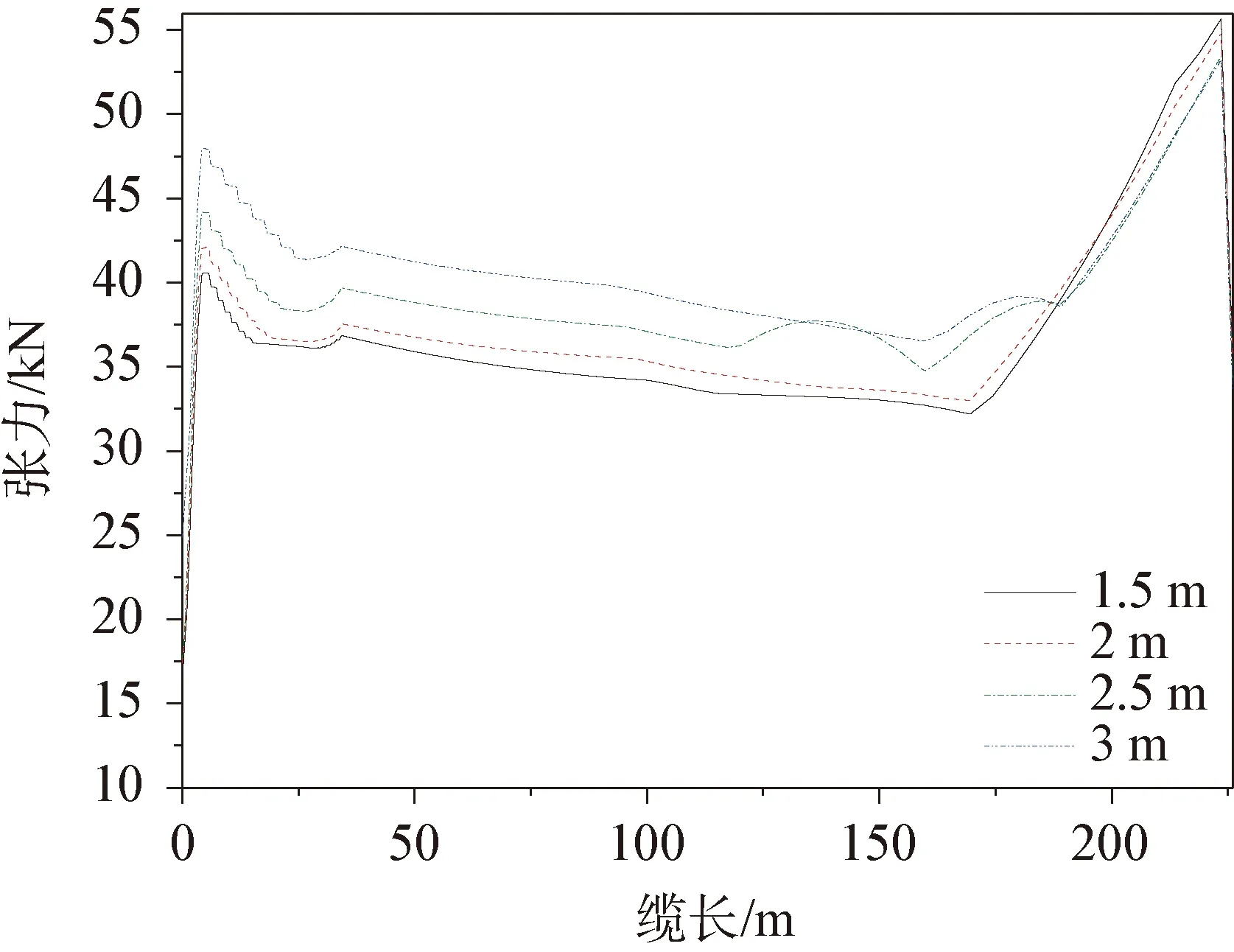
圖17 沿纜長方向的張力分布(工況2)

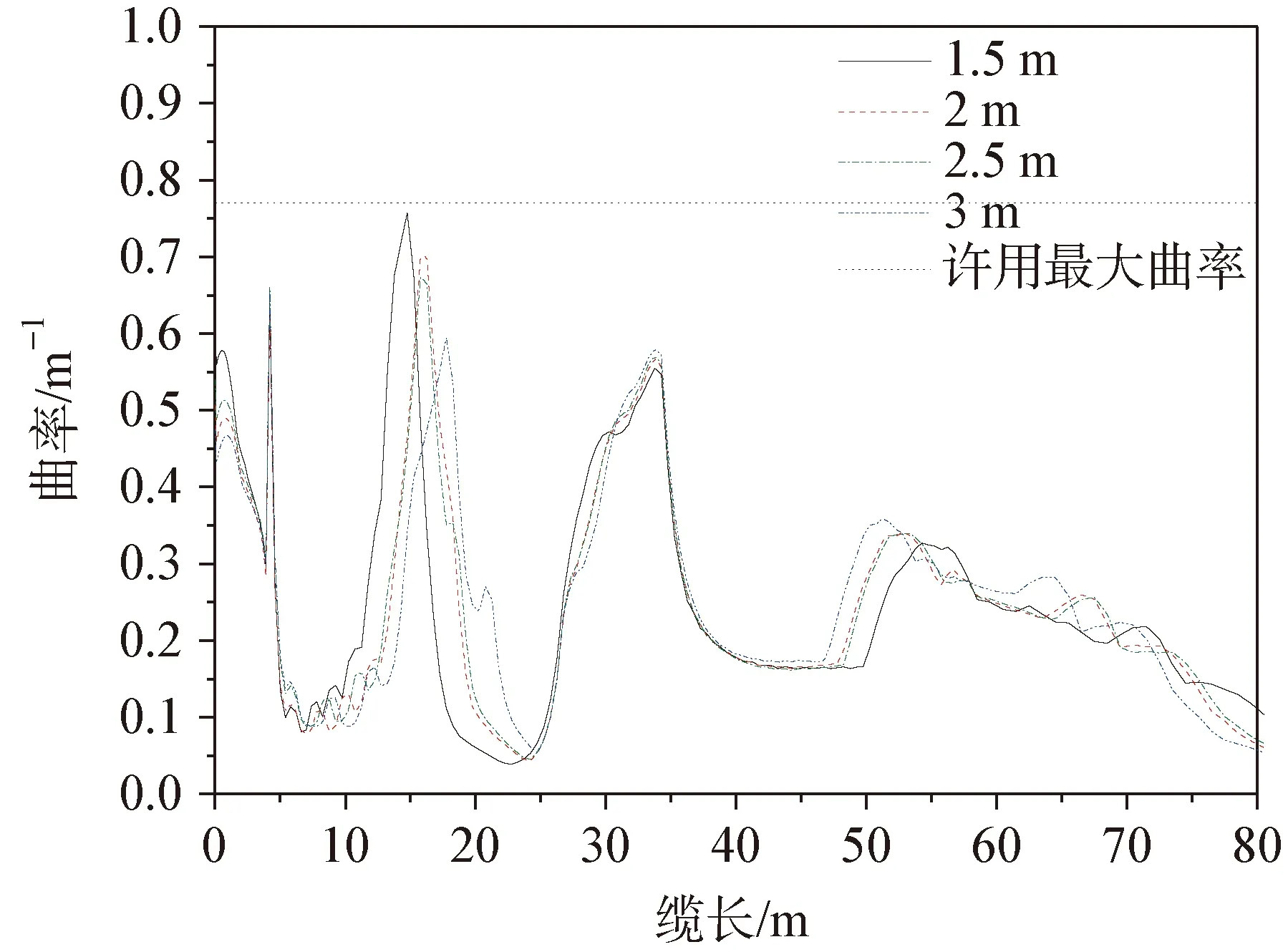
圖18 沿纜長方向的曲率分布(工況1)

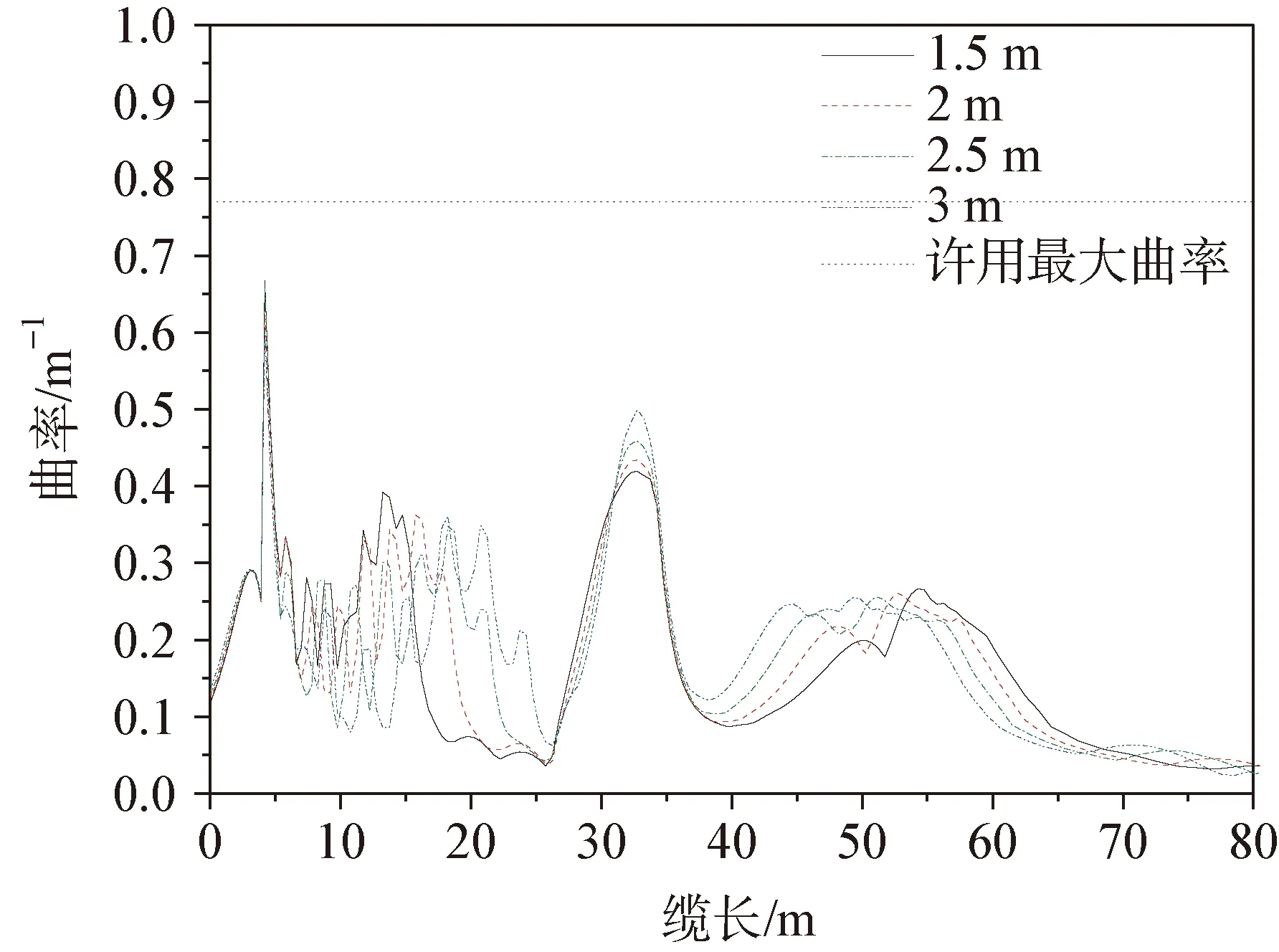
圖19 沿纜長方向的曲率分布(工況2)

綜上所述，最終重塊采用0.2 t×7個×間隔3 m的方案，表6為最終方案在12組工況下的極值分析結果，結果顯示該線型下的最大曲率均能滿足許用最大曲率的要求。張力滿足要求。

表6 最終線型的極值分析結果

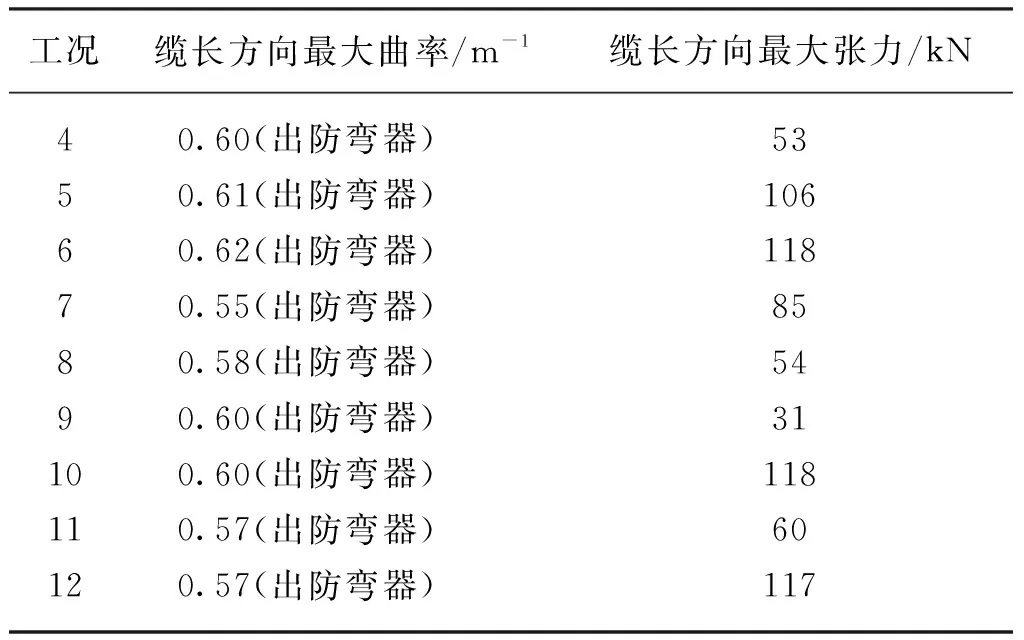
(續 表)

4 結 語

針對浮式風用機動態電纜進行了線型設計，在惡劣海況下傳統的線型設計無法滿足設計要求。通過添加重塊可改善在淺水大偏移條件下纜的受力，在其他條件均保持不變的情況下討論了重塊重量、重塊個數、重塊間距對動態纜結構響應的影響。添加重塊后的動態纜曲率極大值點出現在出防彎器位置和出重塊位置，出防彎器位置曲率將隨著重塊重量/個數的增加而減小，出重塊位置曲率則隨著重塊重量/個數增加而增大。張力極大值點出現在出防彎器位置，隨著重塊重量/個數增加而減小。重塊間距會同時影響重塊段長度以及單位長度上重量，須根據具體工況進行分析，選擇最適合的重塊間距。