環錠數碼紗Kubelka-Munk雙常數配色模型構建及其色彩預測

張婷婷， 薛 元， 賀玉東， 劉曰興， 張國清

(1. 生態紡織教育部重點實驗室(江南大學)， 江蘇 無錫 214122；2. 愉悅家紡有限公司， 山東 濱州 256623)

環錠數碼紡紗系統是數碼紡紗技術與環錠紡紗技術相互結合的產物，是一種能對粗紗喂入比例及成紗線密度進行實時在線控制的新型紡紗方法[1-2]。環錠數碼紡可紡制以3種顏色為基礎的任意混紡比例組合的混色紗。這種新型混色紗的顏色效果是通過多束色纖維須條在紗條中螺旋平行空間排列形成的[3]，其顏色的形成方式既不是單一的光線加法混和，也不是色料的減法混合，而是基于一定面積內同時存在多種色纖維形成的空間混合。混色紗顏色表達的復雜性使得如何準確快速地進行紗線配色成為色紡紗產品開發的關鍵環節[4]。為此提出將計算機測配色與環錠數碼紡技術結合，使得測配色與紡紗在同一工序中完成，進一步縮短工藝流程，提高生產效益。

本文以Kubelka-Munk雙常數理論[5]為模型進行環錠數碼混色紗的測配色研究，選用品紅、黃、青、黑、白5種顏色粗紗為原料，紡制90種不同顏色、不同混紡比的混色紗和5種基色的單色紗，并織成織物，測定其色度參數與不同波長下的反射率；選用相對值法[6]處理Kubelka-Munk雙常數理論，對環錠數碼紡混色紗的測配色模型進行構建，并對配色算法進行預測效果分析，發現此模型預測效果優良，適用于環錠數碼紡混色紗的配比預測。

1 實 驗

1.1 樣品的制備

1.1.1 環錠數碼紡混色紗的制備

實驗原料采用規格為4.2 g/(10 m)的品紅、黃、青、黑、白5種顏色的粗紗；細紗設計為線密度19.4 tex、捻系數340的Z捻向混色紗；紡紗設備為JWF1551型環錠數碼細紗機。將5種不同顏色的粗紗兩兩相互組合，可得到10種顏色組合模式，如表1所示。以10%為梯度(共9種混紡比)制備90種混色紗，并且用相同的紡紗工藝將5種單色紗制備完成。

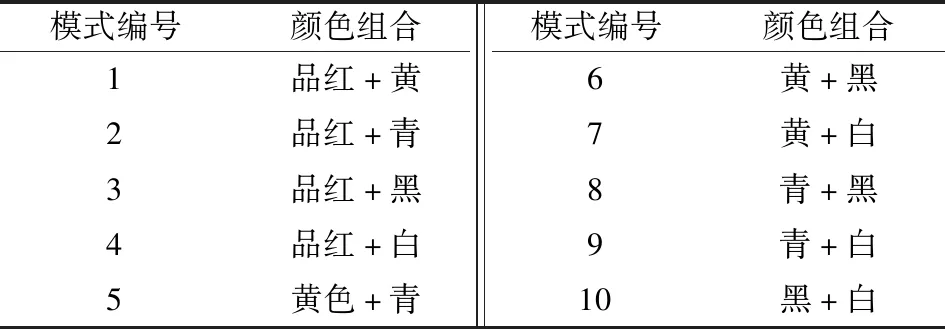
表1 雙通道粗紗顏色組合模式Tab.1 Dual channel roving color combination mode

設粗紗定重為ρ，混色紗線密度為Tt，前區牽伸比為Eq；混紡比為α1的粗紗通道為主牽伸通道(α1≥50%)，其總牽伸比為E1，后區牽伸比為Eh1；混紡比α2的粗紗通道為輔牽伸通道(α2<50%)，其總牽伸比為E2，后區牽伸比為Eh2。雙通道牽伸比計算公式為：

(1)

(2)

(3)

(4)

1.1.2 環錠數碼紡混色紗織物的制備

將紡制的95種紗線用16 G宏成HC21K型緯編圓機織造成平針織物。針織物主要規格如下：線圈長度為0.6 mm；橫密為53縱行/(5 cm)；縱密為90橫列/(5 cm)。 圖1示出部分針織實物圖。

1.2 樣品的顏色測試

將織造的95種針織物用Datacolor 650分光光度計進行顏色測試。實驗環境為D65光源、10°標準觀察者、30 mm測試孔徑，其中光源波長范圍取380～700 nm，以10 nm為間隔取樣。每種比例取12塊針織物樣布為測試對象，每塊樣布任選36個部位進行反射率及色度參數測試，取其平均值分析討論。表2示出5種基礎單色紗線織物色度參數值；表3示出青黑兩色粗紗在混紡比為5∶5時紡制的織物在不同波長下的反射率。

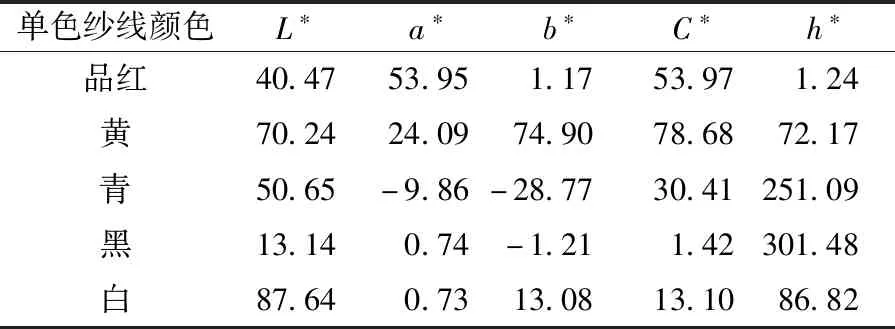
表2 單色紗線織物色度參數Tab.2 Monochrome yarn fabric colorimetric parameters

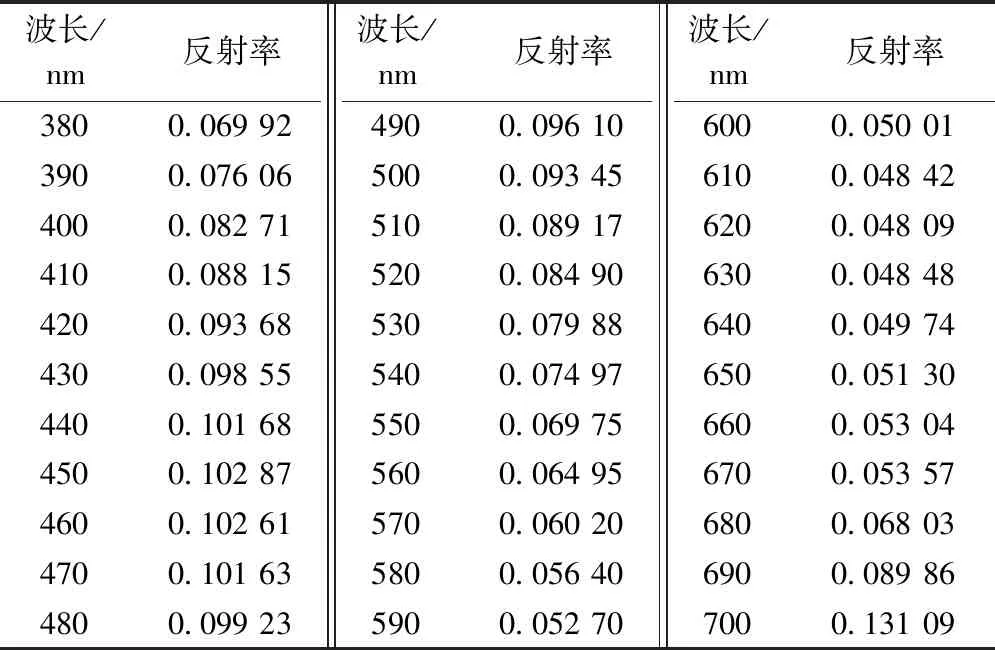
表3 不同波長下的反射率Tab.3 Reflectance at different wavelengths

2 配色模型構建

Kubelka-Munk理論表達式如下。

(5)

式中：K、S分別為被測物體的吸收系數和散射系數；ρ∞為厚度無窮大時的反射率因數。

由于Kubelka-Munk理論是建立在一系列的假定條件基礎上[7]，且只涉及反射率、吸收系數和散射系數，一定程度上限制了其應用范圍，因此在假定染料分子溶解于纖維，忽略染料濃度的同時，根據K/S的加和性，建立了Kubelka-Munk雙常數理論，表達式如下。

(6)

式中：c1、c2、…、cn為染料比例(在纖維混合時指各組分混合比例)；K1、K2、…、Kn和S1、S2、…、Sn分別為不同染料(色纖維)的吸收系數和散射系數，Kt和St分別為基質的吸收系數和散射系數。

Kubelka-Munk雙常數理論中，混色樣擬合反射率的計算如式(7)所示，由混色樣的反射率R計算出K/S值，進而求解得出各單色纖維的吸收系數K和散射系數S，并根據求出的參數K、S計算得到混色樣每個波長下的擬合K/S值，從而得到混色樣的光譜反射率，通過CMC(2∶1)色差公式計算來表征二者的擬合程度。對于吸收系數K和散射系數S的求解，本文通過相對值法進行計算，并對其擬合程度進行比較。

(7)

式中：(K/S)λ為一定波長λ下的K/S值；R為特定波長下的反射率，%；(K/S)m為混色樣的K/S值。

2.1 相對值法

Kubelka-Munk雙常數理論中，對于2種色纖維混合來說，存在以下函數關系：

(8)

式中：C1+C2=1，C1和C2為混色樣的混紡比，(K/S)m為雙混色樣的K/S值，(K/S)1、(K/S)2分別為2種單色纖維的K/S值。

聯立方程組可得：

(9)

K1=(K/S)1×S1

(10)

通過上述求解吸收系數K和散射系數S時，假定其中一種纖維各個波長下的散射系數均為1，這里不妨設S2=1，根據單色纖維反射率計算得出K/S值，進而得出K2，同時相應求出另一種單色纖維的吸收系數K1和散射系數S1，波長范圍同樣取380到700 nm，取樣間隔為10 nm，但這種方法計算的K值和S值僅僅是2種顏色纖維組合在一起相對產生的，是相互依附的，并非單色纖維本身固有的K值和S值，并不能直觀表征色纖維的顏色。

同時為避免上述取樣比例及比例組合的影響，本文單色纖維K值和S值的測定同樣采用9組混色樣構建方程組，設定黑色纖維各個波長下的散射系數均為1，計算各色纖維各個波長下的K值和S值，取均值，如圖2、3所示。

由于相對值法建立的基礎是假定某一種純色纖維每個波長的散射系數S全部為1，那么所計算得到純色纖維的K/S值則與實際測得的是完全相同的，也就是說擬合純色纖維的反射率與實際測得的反射率也是一致的，故本部分在上述各單色纖維K值和S值求解的基礎上，直接選取部分混色樣本的反射率預測曲線和實測曲線如圖3所示，選取樣本與上述相同。

從上圖反射率的擬合效果可以看出，擬合的混色樣反射率曲線與實測反射率曲線能夠實現較好的吻合。在此基礎上，計算出所有預測樣與混色樣的色差,表4示出10種顏色組合5個混紡比的擬合色差。

通過分析可以發現，由相對值法計算吸收系數K和散射系數S所得到的不同顏色組合預測樣和混色樣的擬合色差大部分均在可接受范圍內，表明所建立的顏色預測模型實用性優良，為建立配方預測模型打下基礎。

3 配色算法構建及預測效果分析

3.1 Kubelka-Munk雙常數理論配色算法

在實現Kubelka-Munk雙常數理論的配色算法構建的過程中，是在已知各單色纖維的吸收系數K和散射系數S的前提下進行光譜反射率曲線的擬合以達到預測配方的目的，目標是為了實現在相同的波長下，預測樣的K/S值與混色樣的K/S值相同。即二者存在以下關系：

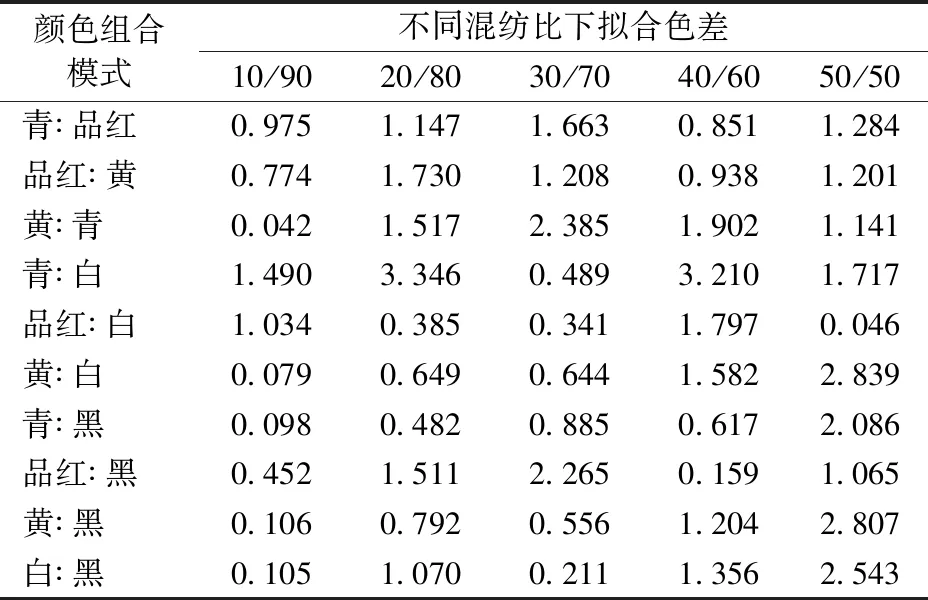
表4 相對值法擬合色差Tab.4 Color differences fitted by relative value method

(K/S)sλ=(K/S)mλ

(11)

式中：λ表示波長，nm；(K/S)sλ表示在波長為λ時預測樣的K/S值；(K/S)mλ表示在波長為λ時，混色樣的K/S值。

對于多組分混色預測樣本，混色樣K/S值與各組分單色纖維的K值和S值存在以下關系：

(12)

式中：C1+C2+…+Cn=1，各波長下每種組分單色纖維的吸收系數K和散射系數S是上文中通過相對值法計算得到的。

將上述公式展開移項得：

(13)

(14)

在各波長下，設

(15)

定義系數矩陣

因此線性方程轉化為

Y=AC

(16)

由最小二乘法[8]求解可得各組分纖維

C=(AT×A)-1×A-1×Y

(17)

3.2 Kubelka-Munk雙常數理論預測效果

為驗證上述算法的準確性和可靠性，采用品紅(M)、黃(Y)、青(C)3種單色纖維組合按照不同配比制備36種混色樣作為目標樣進行配方預測，樣品制備方法、數量和測試方法與上文相同，在配方預測的基礎上計算預測色差，以二者的準確性對預測模型進行評價。

在設定青色纖維各個波長下的散射系數均為1的基礎上，計算出各色纖維各個波長下的K值和S值，在此基礎上采用Kubelka-Munk雙常數理論構建全色譜配色算法[9-10]對上述制備的36種混色樣本進行配方預測和計算預測色差。部分樣本的混合比例、CIELAB色度值和預測色度值、預測比例及即預測色差的結果如表5所示。

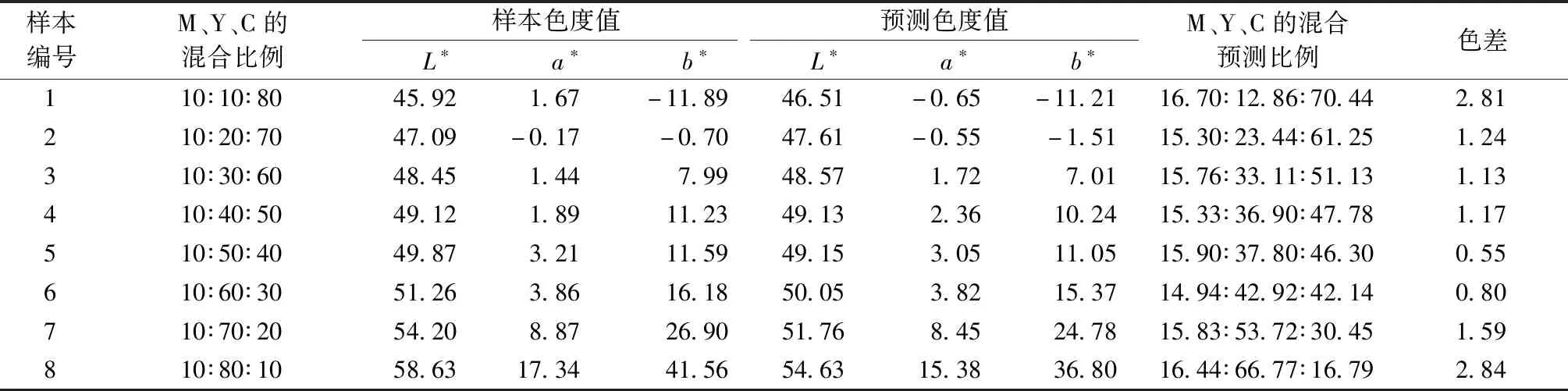
表5 Kubelka-Munk雙常數理論預測結果Tab.5 Prediction results based on Kubelka-Munk double constant theory

注：M表示品紅色纖維；Y表示黃色纖維；C表示青色纖維。

通過基于Kubelka-Munk雙常數理論構建的全色譜配色算法對36種3次色混色樣品進行了配方預測和預測色差，在此基礎上，通過計算樣本平均色差及各色差層級分布占比和預測樣本的平均比例誤差對預測的精度進行分析，其結果見表6，預測樣本的平均比例誤差如式(18)所示。

(18)

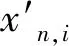
表6 Kubelka-Munk雙常數理論測配色精度分析Tab.6 Kubelka-Munk double constant theory measurement color matching precision analysis

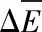
分析表6可發現，Kubelka-Munk雙常數理論所預測的樣本色差均值在可接受范圍內，從色差分布來看，ΔE≤2的情況已經包含了絕大部分，且平均比例誤差較小，色差預測效果優良，證明該模型適用于環錠數碼紡混色紗的顏色預測。

4 結 論

本文以Kubelka-Munk雙常數理論為基礎對環錠數碼紡混色紗測配色進行研究。采用相對值求解參數吸收系數和散射系數并進行模型構建；結合全色譜算法和最小二乘法進行配色算法的構建，從而實現對環錠數碼紡混色紗的顏色預測與配方預測，在總體樣本評價過程中，分別對預測樣本色差均值、色差分布及預測樣本的平均比例誤差進行分析，證實了本理論模型的可行性。

環錠數碼紡混色紗因富有立體感的紋理效果和獨特的色彩呈現方式，符合現代消費者追求個性化、時尚化的服飾消費理念，有著廣闊的發展前景。本文在環錠數碼紡紗系統的基礎上，對色纖維混色模型進行研究，并構建其測配色算法，對推進色紡紗智能化生產，提高色紡紗生產效率有重要意義。