可移動(dòng)載荷彎曲梁實(shí)驗(yàn)設(shè)計(jì)與理論研究

孫傳松，張東煥，周繼磊

(山東理工大學(xué) 交通與車輛工程學(xué)院, 山東 淄博 255049)

面對(duì)材料力學(xué)教學(xué)體系的改革，對(duì)于傳統(tǒng)的材料力學(xué)四大實(shí)驗(yàn)，在創(chuàng)新實(shí)驗(yàn)的新環(huán)境背景下，顯得孤木難支[1]。故學(xué)生實(shí)驗(yàn)教學(xué)形式需要進(jìn)一步改進(jìn)，尤其是新形式的創(chuàng)新性實(shí)驗(yàn)和多角度校核的要求顯得更為迫切。

針對(duì)上述問題，國(guó)內(nèi)諸多學(xué)者從不同角度和形式對(duì)彎曲梁實(shí)驗(yàn)進(jìn)行了研究和拓展，其中包括理論與實(shí)驗(yàn)的校核、材料力學(xué)與彈性力學(xué)解的對(duì)比[2]、實(shí)驗(yàn)與有限元仿真的結(jié)合、不同梁與不同加載形式的豐富組合等等。陳玉驥[3]推導(dǎo)了單跨超靜定梁在均布載荷作用下的彈性力學(xué)解析解，利用半逆解法，求出研究對(duì)象的應(yīng)力和位移。張偉等[4]就集中載荷作用下兩端固支的超靜定梁進(jìn)行了彈性力學(xué)解的推導(dǎo)，利用半逆解法研究了彎曲梁的應(yīng)力和位移的多項(xiàng)式解，為工程設(shè)計(jì)以及彈性力學(xué)教學(xué)提供了重要參考。何曉婷等[5]就不同模量簡(jiǎn)支梁在均布載荷下的彈性力學(xué)解進(jìn)行了推導(dǎo)，研究表明，不同的彈性模量，應(yīng)力分布差異較大，且材料力學(xué)中的最大正應(yīng)力會(huì)被低估。魯華賓等[6]通過有限元軟件Abaqus對(duì)純彎曲梁進(jìn)行了實(shí)驗(yàn)?zāi)M。王曉琴等[7]研究和推導(dǎo)了均布載荷作用下懸臂梁的彈性力學(xué)解，研究表明，與彈性力學(xué)理論解相比，材料力學(xué)對(duì)于深梁的計(jì)算結(jié)果存在較大誤差。盧玉林等[8]就中間受到集中力作用時(shí)的彎曲梁正應(yīng)力進(jìn)行了理論推導(dǎo)和實(shí)驗(yàn)研究，不僅對(duì)材料力學(xué)解進(jìn)行了校核，更加深了學(xué)生對(duì)理論公式的理解。Eroglu[9]對(duì)功能梯度材料(FGM)制成的平面彎曲梁任意平面內(nèi)的偏轉(zhuǎn)進(jìn)行了研究。Anup等[10]應(yīng)用Euler-Bernoulli理論的運(yùn)動(dòng)學(xué)假設(shè)分析雙向功能梯度(FG)圓形梁的彎曲。蔡瑜瑋[11]對(duì)材料力學(xué)實(shí)驗(yàn)教學(xué)改革進(jìn)行了有益探索，闡述了學(xué)生為主體、教師為主導(dǎo)的觀念，讓學(xué)生自主性開發(fā)組合設(shè)計(jì)實(shí)驗(yàn)的形式。通過以上的研究和探索不難發(fā)現(xiàn)，目前對(duì)材料力學(xué)彎曲梁實(shí)驗(yàn)，越來越注重多角度校核和新形式的探索。

本文從現(xiàn)有的最普遍的彎曲梁實(shí)驗(yàn)器材出發(fā)，以傳統(tǒng)的純彎曲梁實(shí)驗(yàn)為例對(duì)傳統(tǒng)純彎曲梁實(shí)驗(yàn)設(shè)備進(jìn)行改造，設(shè)計(jì)橫向力四點(diǎn)彎曲梁的物理模型。通過推導(dǎo)任意載荷位置下梁的彈性力學(xué)解析解、ABAQUS數(shù)值仿真的模擬值與實(shí)驗(yàn)結(jié)果進(jìn)行校核[12-13]，分析梁在移動(dòng)載荷作用下的應(yīng)力、應(yīng)變分布情況，為進(jìn)一步了解空間梁的力學(xué)特性提供幫助。

1 模型的建立及解析解推導(dǎo)

將現(xiàn)有純彎曲梁實(shí)驗(yàn)的儀器進(jìn)行改造，由原來加載位置不變的兩個(gè)對(duì)稱橫向力變成可以任意移動(dòng)的非對(duì)稱橫向力。實(shí)驗(yàn)通過移動(dòng)連桿完成對(duì)梁上不同位置的載荷施加，實(shí)現(xiàn)梁中間位置的應(yīng)力狀態(tài)由純彎曲狀態(tài)到橫力彎曲狀態(tài)的轉(zhuǎn)變，且可自主改變載荷加載位置，測(cè)量設(shè)備示意圖如圖1所示。

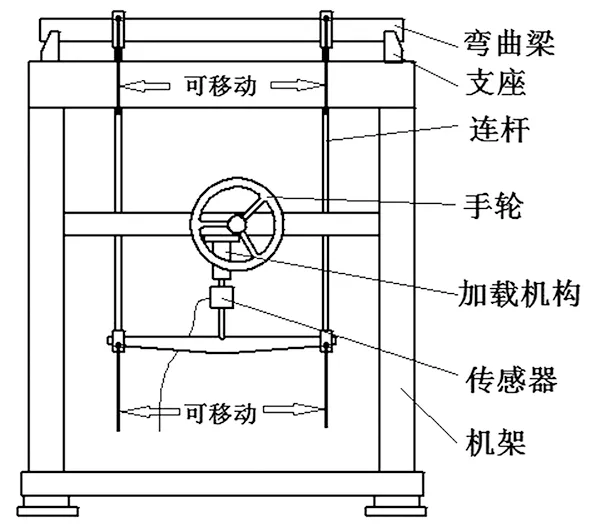
圖1 測(cè)量設(shè)備示意圖

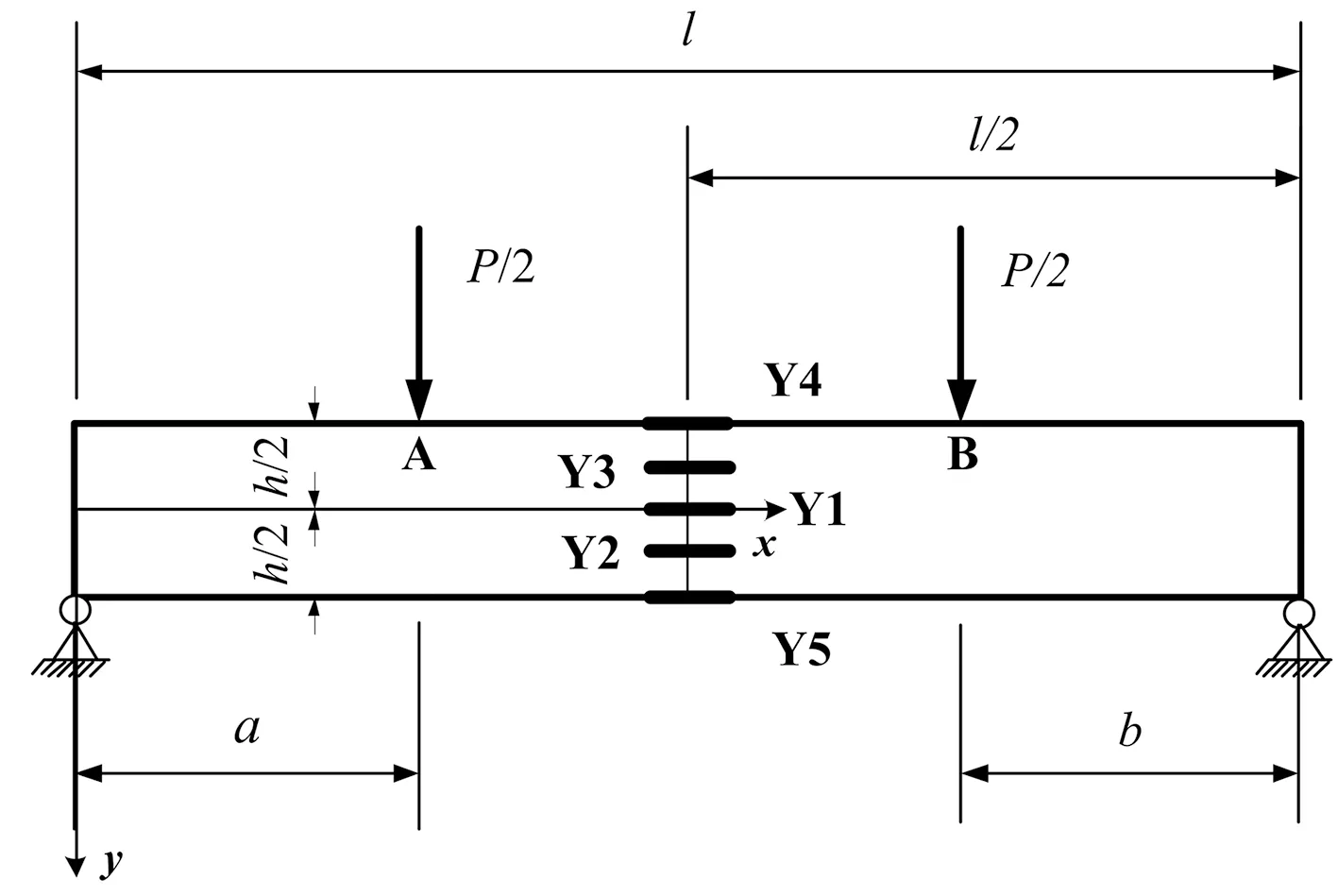
圖2 橫力四點(diǎn)彎曲梁的物理模型

假設(shè)梁的長(zhǎng)度為l，截面高度為h，寬度為k，加載的載荷為P。橫力四點(diǎn)彎曲梁的物理模型如圖2所示。依據(jù)正應(yīng)力邊界條件，切應(yīng)力在y=±h/2時(shí)大小為零，故設(shè)應(yīng)力函數(shù)為φ=xf1(y)+f2[14]，將其帶入相容方程4φ=0，得到待定函數(shù)

(1)

由(1)式得到每一段梁應(yīng)力的應(yīng)力函數(shù)表達(dá)式為

φ=x(Aiy3+Biy2+Ciy)+Hiy3+Kiy2

(2)

根據(jù)載荷所加載的位置，將橫力四點(diǎn)彎曲梁分為3段，其中每一段梁載荷施加處的應(yīng)力函數(shù)分量為通式。待定系數(shù)利用下標(biāo)i代表梁的位置，實(shí)驗(yàn)中A處載荷作用點(diǎn)在x=a處，B處載荷作用點(diǎn)在x=l-b處，故i= 1，2，3，其每一段梁應(yīng)力函數(shù)的應(yīng)力分量表達(dá)式為

(3)

載荷加載處的切應(yīng)力如圖3所示，其各處的受力關(guān)系為[8]

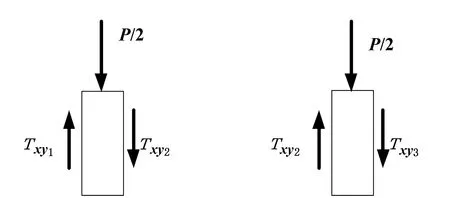
圖3 A、B兩處受力點(diǎn)的狀態(tài)

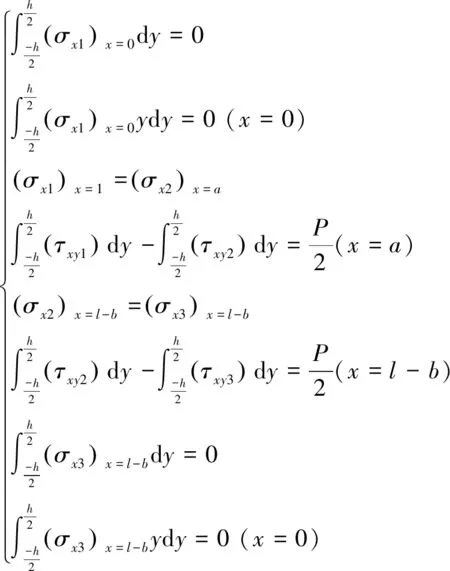
(4)

在圖2所示的物理模型中，無論施加的力在何處位置，梁的上下兩面的切應(yīng)力均為零，即切應(yīng)力在y=±h/2時(shí)大小為零。因此3段梁應(yīng)力分量的待定常數(shù)Bi=0,Ci=-3kh2Ai/4 應(yīng)是一致的，由此可推出3段梁中應(yīng)力函數(shù)的系數(shù)為

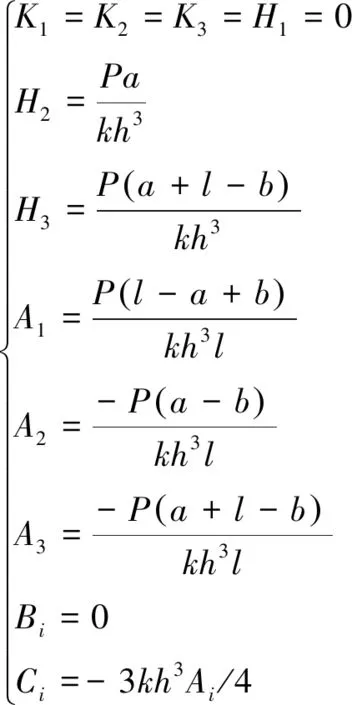
(5)

每段應(yīng)力分量就可以化簡(jiǎn)為

(6)

最后獲得簡(jiǎn)支梁集中載荷下的理論應(yīng)力解為

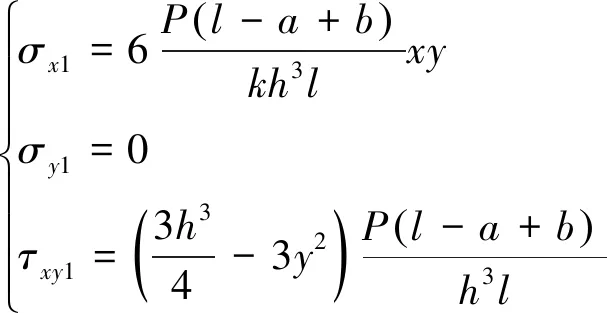
(7)

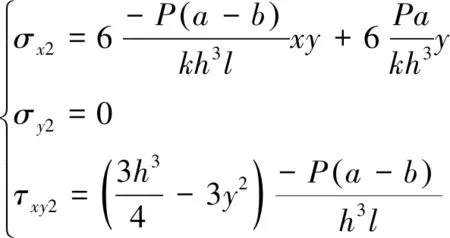
(8)

(9)

當(dāng)a=b，且l>2a時(shí)，即純彎曲實(shí)驗(yàn),得

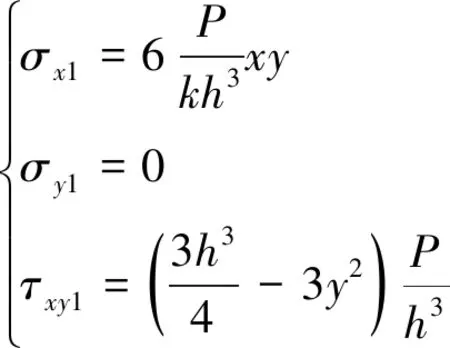
(10)

(11)

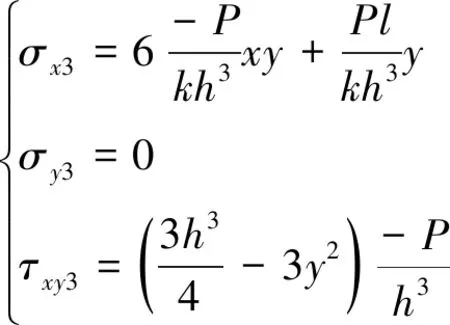
(12)

由公式(7)～(12)可知,當(dāng)梁受距離兩端相等的兩個(gè)力時(shí)，在x=a或者x=(l-b)時(shí)正應(yīng)力相等且最大，與梁在x=a～(l-b)段的正應(yīng)力保持一致，切應(yīng)力為0。即

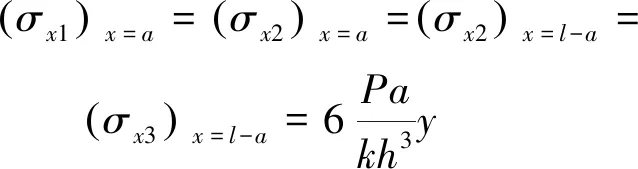
(13)

當(dāng)l=2a時(shí)，即該簡(jiǎn)支梁僅在l/2處受一個(gè)力，該處的正應(yīng)力表達(dá)式與公式(10)～(12)完全相同。證明該彈性力學(xué)正應(yīng)力公式與材料力學(xué)最大正應(yīng)力公式

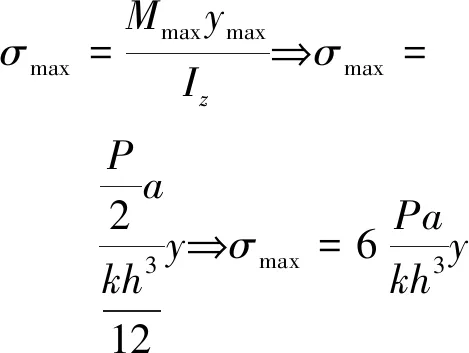
(14)

完全吻合。

2 數(shù)值、實(shí)驗(yàn)驗(yàn)證與誤差分析

為了更好地分析物理模型測(cè)試點(diǎn)的應(yīng)力分布情況，通過實(shí)驗(yàn)研究和數(shù)值模擬進(jìn)行驗(yàn)證。

實(shí)驗(yàn)試樣為低碳鋼，材料屬性和尺寸見表1。采用圖1所示實(shí)驗(yàn)形式，取a=150 mm，b=100 mm，加載機(jī)構(gòu)對(duì)彎曲梁依次加載500 N、1 500 N、2 500 N、3 500 N、4 500 N的載荷。應(yīng)變片的位置處在梁的中間位置(如圖2所示)，其具體位置見表1。取梁的中間截面為研究對(duì)象，應(yīng)變片處獲得的實(shí)驗(yàn)數(shù)據(jù)見表2。

采用本文推導(dǎo)的理論解析公式得到該處的應(yīng)力情況。

表1 梁的材料屬性、尺寸及應(yīng)變片位置Tab.1 Beam material properties, dimensions, and strain gauge locations

材料彈性模量E/GPa高度h/mm寬度k/mm距離l/mm應(yīng)變片至中性層的距離/mmY1Y2Y3Y4Y5低碳鋼21040205000-101020-20

表2 實(shí)驗(yàn)數(shù)據(jù)Tab.2 Experimental data

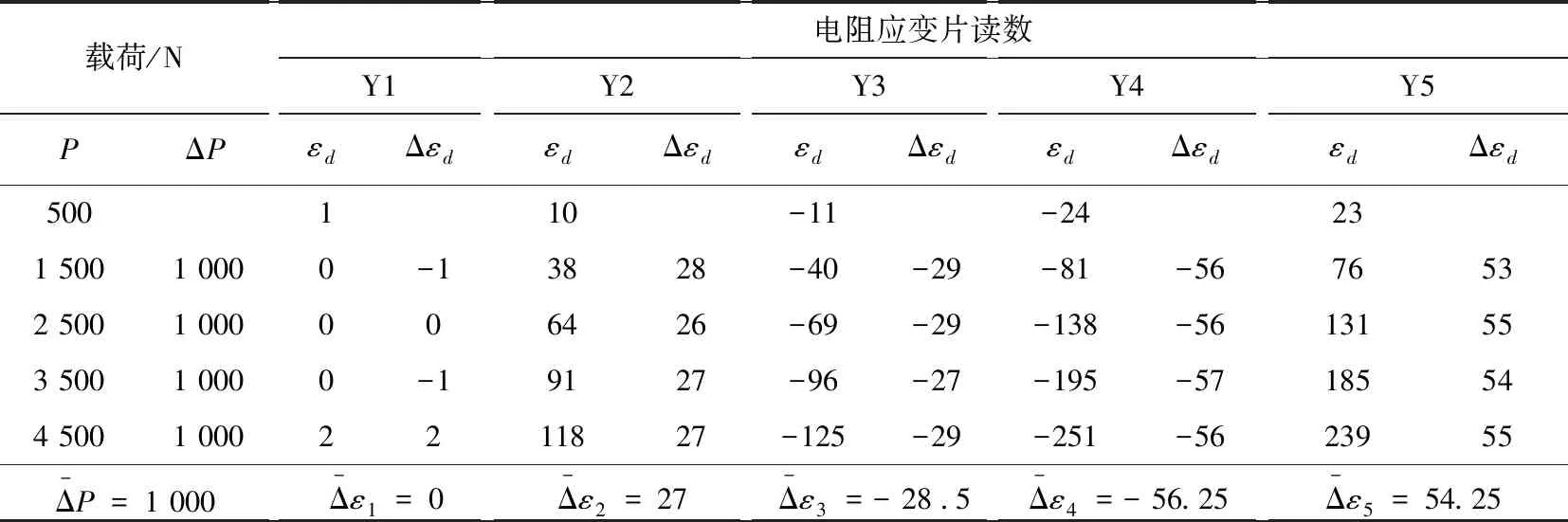
載荷/N電阻應(yīng)變片讀數(shù)Y1Y2Y3Y4Y5PΔPεdΔεdεdΔεdεdΔεdεdΔεdεdΔεd500110-11-24231 5001 0000-13828-40-29-81-5676532 5001 000006426-69-29-138-56131553 5001 0000-19127-96-27-195-57185544 5001 0002211827-125-29-251-5623955Δ-P=1 000Δ-ε1=0Δ-ε2=27Δ-ε3=-28.5Δ-ε4=-56.25Δ-ε5=54.25

下面通過有限元軟件ABAQUS 6.14對(duì)上述實(shí)驗(yàn)結(jié)果進(jìn)行模擬，模型材料為低碳鋼，泊松比為0.3，長(zhǎng)度、寬度、高度參數(shù)見表2。在集中力施加處設(shè)參考點(diǎn)，將受力處節(jié)點(diǎn)設(shè)置為結(jié)點(diǎn)集并均勻地耦合在參考點(diǎn)上。模型的右端在中性層處施加鉸接的邊界條件，左端中性層部分施加限制2、3方向的轉(zhuǎn)動(dòng)與平動(dòng)的邊界條件。在施加載荷處施加2方向-P/2=-500 N的力。網(wǎng)格采用結(jié)構(gòu)型網(wǎng)格畫法，C3D20R單元:二十結(jié)點(diǎn)二次六面體單元。所得結(jié)果如圖4所示。

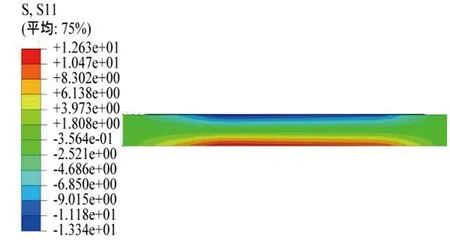
圖4 模型正應(yīng)力分布圖

取中間中性層為對(duì)稱面，在Y軸方向上下各采集4個(gè)節(jié)點(diǎn)進(jìn)行數(shù)據(jù)與繪圖分析，結(jié)果如圖5所示。

將實(shí)驗(yàn)結(jié)果、理論解析與數(shù)值模擬進(jìn)行匯總和比較，結(jié)果見表3。由表3可知，橫力四點(diǎn)彎曲梁的物理模型理論解析解結(jié)果與模擬仿真結(jié)果誤差近乎0%。理論結(jié)果、數(shù)值結(jié)果與實(shí)驗(yàn)結(jié)果除中性層外平均誤差為2.3%。證明了該實(shí)驗(yàn)理論的正確性。

圖5 應(yīng)變片橫截面數(shù)值模擬

表3 三者結(jié)果對(duì)比及誤差分析Tab.3 Comparison of expenimental,theoratical and numerical results and error analysis

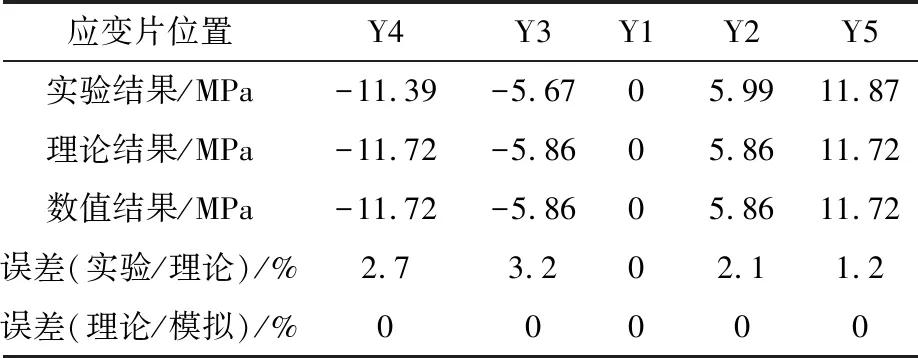
應(yīng)變片位置Y4Y3Y1Y2Y5實(shí)驗(yàn)結(jié)果/MPa-11.39-5.6705.9911.87理論結(jié)果/MPa-11.72-5.8605.8611.72數(shù)值結(jié)果/MPa-11.72-5.8605.8611.72誤差(實(shí)驗(yàn)/理論)/%2.73.202.11.2誤差(理論/模擬)/%00000

3 結(jié)束語

本文將現(xiàn)有受固定載荷作用的純彎曲梁實(shí)驗(yàn)設(shè)備拓展為兩處受移動(dòng)載荷作用的橫向力四點(diǎn)彎曲梁實(shí)驗(yàn)設(shè)備。推導(dǎo)了任意載荷位置下彎曲梁的彈性力學(xué)解析解，并通過數(shù)值模擬和實(shí)驗(yàn)驗(yàn)證了實(shí)驗(yàn)結(jié)果與理論推導(dǎo)結(jié)果基本一致。本研究豐富了材料力學(xué)彎曲梁的實(shí)驗(yàn)形式，完成了材料力學(xué)彎曲梁實(shí)驗(yàn)深層次的探究和認(rèn)識(shí)，促進(jìn)了學(xué)生對(duì)理論公式的理解，加深了學(xué)生對(duì)力學(xué)中各角度分析的意識(shí)，可為后續(xù)的力學(xué)相關(guān)實(shí)驗(yàn)教學(xué)提供參考。