基于NAO機器人的行走約束研究

，，

(沈陽建筑大學機械工程學院，遼寧 沈陽 110168)

0 引言

從20世紀中后期早稻田大學制造出WABOT-1型機器人開始，人們對人形機器人的研究一直在不斷進步。2000年本田公司制造ASIMO機器人，隨后又在2011年推出了全新的ASIMO以及人形機器人HRP-4C和Robonaut2[1]。幾年后，NAO機器人的橫空出世可見人形機器人的發展之快，而本文以NAO機器人進行研究。

對于人形機器人的運動軌跡研究有幾種方法，如以動力學分析為基礎的步行規劃方法[2]；基于捕捉人體運動的步態規劃方法[3]；基于ZMP理論的步態規劃[4]；基于被動步行的步態生成方法[5]；基于倒立擺模型的方法[6]；基于能量最優化的方法[7]；基于多連桿模型的方法等[8]。此前方法多數已經成功而且應用在實際的機器人上[9-11]。

然而以上研究，機器人的骨盆運動與自由足所受到的限制并未納入考慮范圍，因此無法完全控制零力矩點(ZMP)從而無法保證機器人穩定的行走。基于此提出約束行走規劃，使機器人的腳與地面充分接觸，即使由于機器人行走過程中骨盆運動和自由足所受到的限制，也能實現機器人的穩定行走。

1 NAO機器人及運動學分析

NAO機器人是由Aldebaran機器人公司制造的可編程人形機器人。具有25個自由度，每只手臂5個、每個腳1個、頭部2個、腿部11個；身高0.57 m，體重4.5 kg。該機器人如圖1所示。其腿部的運動模型如圖2所示。每條腿上有6個旋轉關節，但由于關節與骨盆相連，其運動會受到限制，而上面有1個制動器來產生對稱旋轉。

圖1 Aldebaran公司NAO仿人機器人

為了更好地理解NAO機器人的運動模式，采用改良的D-H參數法(Denavit和Hartenberg參數法)對NAO機器人腿部建立運動學模型。每個連接處都附上一個正交參考坐標系。連接點的編號為0～12，從固定連接點開始(支撐足)，到移動腳(自由足)結束，如圖2所示，能夠看出正交坐標系XM，YM和ZM是建立在地面坐標(全局坐標系)上。

為了展開運動分析，在同一個運動鏈上建立了2套參考坐標系：一個是針對右側固定足(frf)，另一個是針對左側固定足(flf)。圖2中顯示的運動鏈是右側固定足。對于frf和flf來說，坐標系編號都從零開始，指定到固定足。表1列出了腿部運動鏈的改良后D-H參數。這些參數對于frf和flf 2條鏈來說都是一樣的。表1中非空距離數值為d3=d11=0.103 m，d4=d10=0.10 m，r6=r7=0.071 2 m。

圖2 NAO機器人腿上的運動坐標系示意

各個連桿和關節處的局部坐標系的設定方法是：與連桿或是關節i相關的坐標系成為坐標系{1}其中i=1,2，…，12。αi表示繞Xi軸，從Zi旋轉到Zi+1的角度；

di表示繞Zi軸，從Xi-1移動到Xi的距離；

θi表示繞Zi軸，從Xi-1旋轉到Xi的角度；

τi表示骨盆到左右連桿水平延長線的距離。

表1 改進后NAO雙腿的D-H參數

根據圖3所示的動力傳輸結構能夠看出一個簡單的電機如何為運動鏈骨盆上的關節6和關節7提供運動。因此，以下約束來自動力傳輸θ6=θ7。

移動狀態下的機器人明顯約束了運動鏈的機動性，這時候方程式成立。由圖3可知，附著于骨盆的一個正交參考坐標系(參考坐標系xp-yp-zp)。

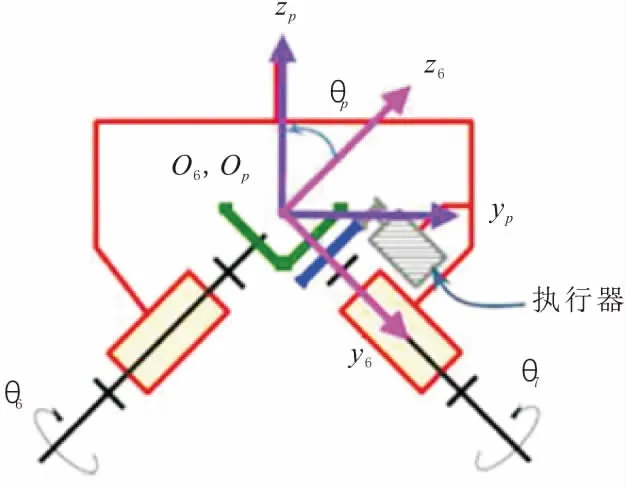
圖3 向附著于骨盆的關節傳輸動力的結構

這個坐標系通過固定角θp相對于坐標系6的x6軸轉動。其中，frf的θp=45°，而flf的θp=-45°。

2 NAO機器人行走規劃

規定附著于骨盆(坐標系xp-yp-zp，如圖2所示)的坐標系姿態(位置與方向)以及相對于全局坐標系的自由足(坐標系x12-y12-zp12)作為時間函數，以此定義正常行走模式。當行走過程中，坐標系xp-yp-zp保持平行于坐標系xm-ym-zm，而且自由足腳底保持平行于全局坐標系的平面xm-ym時，就能夠獲得人形機器人的一個特定行走情形。這種行走就是本文中所定義的基本行走。

在這種行走情形下，軀干的位移僅限于平移，而自由足則是普通運動，而且受限于圍繞的旋轉運動。可利用與全局坐標系相匹配的本坐標系開始處相應連接點附著的Bryant角度λ，μ和υ，來規定骨盆與自由足相對于全局坐標系的理想方向。因此，在基本行走模式中，骨盆的3個Bryant角度都是零位，因此骨盆相對于全局坐標系的旋轉矩陣為

(1)

對于正常行走模式中的自由足轉動，規定足部坐標系中矢量x12的方向。為了保持基本行走的條件，這種矢量必須與地面(平面xm-ym)相交。因此，自由足相對于全局坐標系的旋轉矩陣為

(2)

矩陣中的m12，m22，m23等項的定義取決于λ,μ,υ的賦值。在之前有關基本行走模式的分析中，已經證明對于骨盆特定姿態和自由足特定位置，m12，m13，m22，m23必須符合以下方程式要求，即

-c7s8m13+(cPc8+sPs7s8)m23=0

(3)

(4)

Si=sinθici=cosθi(i=7,8);sP=sinθP;cP=cosθP。θ7和θ8分別是圖2所示運動鏈中關節7和關節8的關節變量。

對于基本行走模式來說，自由足的Bryant角度受到約束，其中m12,m13,m22,m23符合式(3)和式(4)，這些方程式被定義為基本行走模式的前提條件。在行走過程中，如果骨盆的OP點路徑保持在機器人矢狀平面上，而自由足的點O12保持在與矢狀平面平行的平面上，就能夠達到上述前提條件。否則，自由足的腳底就不會平行于地板平面，繼而無法實現足部與地面的穩定接觸。

3 行走約束條件

對于NAO機器人的基本行走模式來說，可以實現支撐足的姿態下，讓腳底與地面充分接觸。但是在基本行走模式中，骨盆點OP受到約束，保持在矢狀平面上。這種條件下，單獨支撐階段中的ZMP一般無法保持在機器人的支撐表面上。

為了全面控制ZMP的位置，必須讓點OP的運動構件保持在正面。然而，這樣一個構件會避開基本行走；因此，如果想要改善支撐足腳底中ZMP的位置，必須忽略基本行走的前提條件。提出保持支撐足的充分接觸狀態(式(2))，但卻允許骨盆在正面旋轉與位移。

因此，自由足的位置與方向以及骨盆位置將會被完全指定。骨盆可以旋轉，這樣能夠改善自由腿的機動性，以便適當控制ZMP。為了規定自由足的方向，采用Bryan角度λ12,μ12和v12來定義坐標12相對于全局坐標系的方向。骨盆方向的Bryan角度λp，μp，vp取決于支撐足的關節變量θ4，θ5，θ6。因為λp，μp，vp未明確，所以將θ4，θ5，θ6視為一種優化方法的自變量。

事實上，為了僅通過機器人部分規定運動中的11個自由度解決逆向運動問題，提出一個基于非線性優化方法的數值方案。該方案的各階段劃分如下：分別規定骨盆中點OP和附著于自由足坐標系中點O12的笛卡爾坐標xpypzp和xo12yo12zo12，以及規定相對于全局坐標系的坐標系12方向的Bryant角度λ12，μ12，v12。提出關節變量的初始值θ4，θ5，θ6。從提出的初始值θ4，θ5，θ6開始，將以下目標函數最小化，即

(5)

圖4 骨盆的運動

圖5 雙足位置

圖6 右足的方向

圖7 左足的方向

4 仿真結果

在圖4和圖7中展示出相對于在限定條件下的骨盆和自由足的理想運動曲線。通過ZMP軌跡曲線來確定對骨盆運動的限制改善單支撐階段的ZMP控制，先計算ZMP軌跡，結果如圖8所示。

根據圖8所示，實際ZMP曲線與理想曲線在部分地方差別較大，但通過限制骨盆移動后，在部分區域使之與理想曲線更加重合接近。

圖8 ZMP曲線

如圖9所示，對骨盆和自由足的理想運動通過加以規定，僅對骨盆的旋轉運動進行合成。特定行走時間為每步0.5 s。行走包含4步，第1步相當于起始階段，而最后一步為結束階段。第2步和第3步處于勻速的巡游階段。表2為各行走階段數據，圖9表示模擬狀態下機器人各部行走的狀態。從1 s開始時自由足與固定足的切換，直到2 s結束時，機器人的穩定狀態模擬圖像。

表2 約束后理想運動的各部分參數值

圖9 行走模擬

5 結束語

當規定的Bryant角得到約束就能夠實現機器人的持續運動以及每一步中自由足與地面之間的穩定接觸。這樣有助于解決NAO仿人機器人11個自由度腿部的逆運動問題。當自由足的運動得到全面規定，骨盆中只規定了1個點的路徑，骨盆的平移運動能夠改善單支撐階段ZMP的控制。與此同時合成骨盆的旋轉運動，進而對自由足姿態實現全面控制。對于NAO機器人步態的研究中，較大程度改善行走過程中ZMP的行為。為人形機器人行走機構的數據參數分析提供支持，進而為機器人及其相關輔助機械設備研究提供幫助。