任意荷載下連續排水邊界分數階黏彈性地基一維固結模型

王玨，童立紅，金立，徐長節,3

(1. 華東交通大學 江西省巖土工程基礎設施安全與控制重點實驗室，南昌 330013；2. 浙江杭海城際鐵路有限公司，浙江 嘉興 314000；3. 浙江大學 濱海和城市巖土研究中心，杭州 310058)

在Terzaghi固結理論中，土體被處理為線彈性模型，而流變特性是軟土的一種重要的工程特性[1]。因此，考慮軟黏土的流變特性，將土體視為黏彈性介質通常更符合實際工程[2]。Taylor等[3]首先引入Kelvin模型來描述土骨架的黏彈性變形；Tan[4]基于Maxwell模型對受側限土體的固結和滯流進行了研究。此后，金問魯等[5]提出了固結方程的一個近似解法，并給出了各種條件下簡單問題的解答；趙維炳[6]基于廣義Voigt模型，推導了飽和土體一維固結問題的普遍理論解答；Xie等[7-8]引入Merchant模型及四元件模型到固結理論中，分析了軟黏土的固結特性；蔡袁強等[9]求解了任意荷載下成層粘彈性地基一維變形問題。然而，上述經典流變模型不能很好地與實驗數據相吻合[10]，主要是由于整數階微分算子的性質決定了經典流變模型的核函數通常是指數函數的組合，欲精確描述實驗數據，常常不得不取消高階的微分項或者以降低本構模型的應用范圍為代價[11]。

Gement[12]首先提出了黏彈性材料的分數階導數本構模型，而后一些學者將其引入到固結理論中，并指出分數階導數流變模型可以有效克服經典模型的缺點。Koeller[13]用基于分數導數的彈壺元件替換牛頓黏壺，研究分析了多種模型的流變特性；孫海忠等[14]采用含分數導數的Kelvin模型對珠江三角洲南沙地區典型軟土的流變試驗數據進行擬合，得到很好的結果；Yin等[15]對分數階軟土蠕變過程中的力學性能進行了系統的研究；汪磊等[16]基于分數階導數理論引入Kelvin-Voigt模型，獲得了任意荷載情況下一維固結問題的半解析解；劉忠玉等[17]求得了恒載下基于分數階Kelvin模型飽和軟黏土一維固結理論解，并通過對比一維流變固結試驗曲線及整數階模型理論曲線，指出基于分數階Kelvin模型模擬的孔壓消散曲線更接近試驗曲線。

另一方面，實際工程中土體的邊界往往是處于透水與不透水之間的一種中間狀態[18]。蔡袁強等[19]、汪磊等[20]研究了半透水邊界條件下一維固結問題。但是半透水邊界計算相對復雜，且不能嚴格滿足初始條件，限制了土體固結方程解的適用性[21]。基于此，梅國雄等[18]提出了一個從不透水到透水的雙面不對稱連續排水邊界。目前，關于變荷載、連續排水邊界及分數階導數黏彈性模型耦合的一維固結理論分析很少見諸于文獻。筆者針對Caputo分數階導數的彈壺元件修正Kelvin模型黏彈性地基，引入連續排水邊界條件，推導了任意荷載下連續排水邊界分數階黏彈性地基一維固結方程的半解析解，并分析了相關參數對軟黏土固結沉降特性的影響。

1 Caputo分數階導數修正Kelvin模型

在分數階導數流變模型中運用最為普遍的是Riemann-Liouville(R-L)型分數階微積分算子理論[16]，但R-L分數導數在初始點處無物理意義，而Caputo分數導數則克服了這個缺點，其定義為[17]

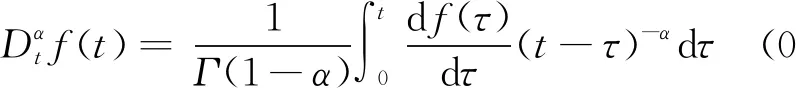
(1)

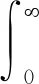
Caputo分數導數的Laplace變換為

(2)

用基于分數導數定義的彈壺元件[13]替換經典Kelvin模型中的牛頓黏壺得到修正的Kelvin模型，如圖1，其微分型本構方程為

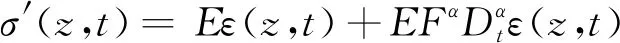
(3)

式中：σ′(z,t)為深度z處t時刻相對于初始有效應力的增量(簡稱有效應力)；ε(z,t)為相應的應變；E為彈性模量；F=η/E，為黏彈性體的延遲時間；η為黏滯系數。當η=0時，即為Terzaghi一維固結理論的彈性模型。當α=1時，該模型退化為經典的Kelvin模型；當α=0時，可退化為兩個彈簧元件并聯的線彈性模型。在實際工程計算中，可采取擬合土樣固結實驗數據的方法得到α的值。

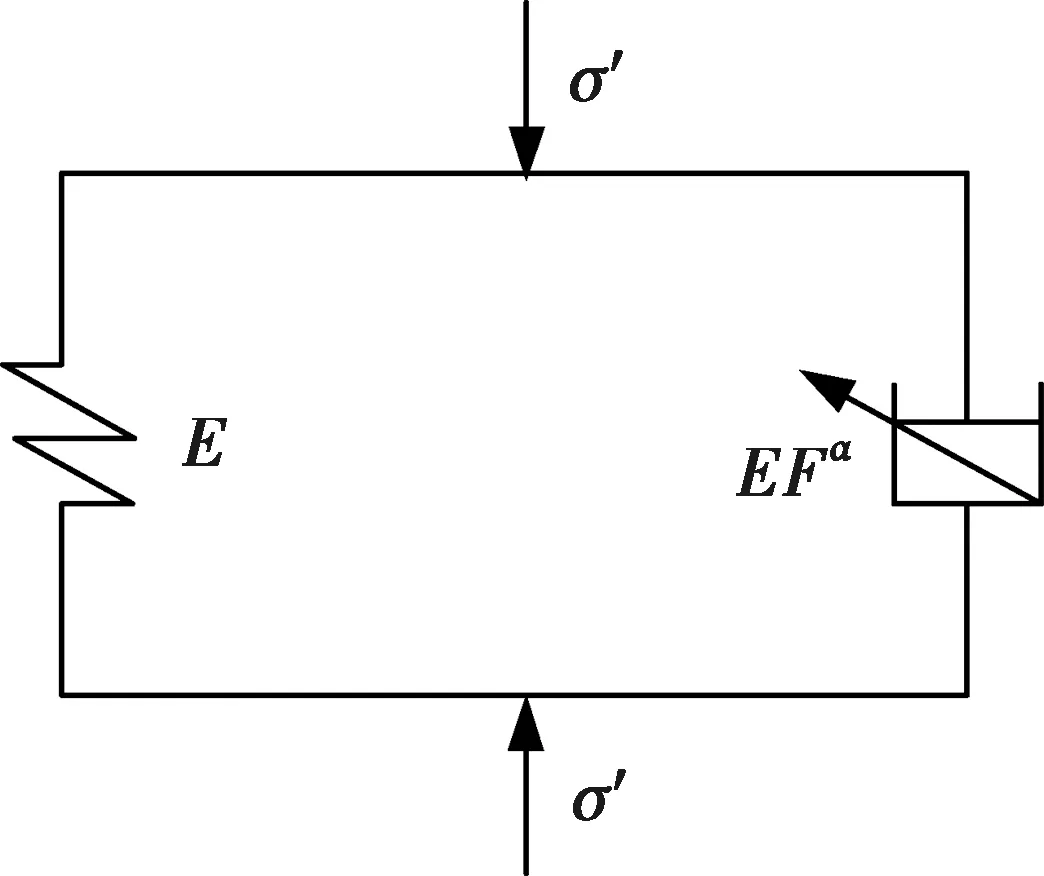
圖1 修正的Kelvin模型

2 流變固結方程的建立及求解

任意荷載下連續排水邊界條件土體固結計算簡圖如圖2所示。圖中p(t)為隨時間變化的任意荷載；H為土層厚度；kv為滲透系數；Cv為固結系數。假設土體完全飽和，孔隙水以及土顆粒都不可壓縮，且僅發生豎向滲流和變形。以修正Kelvin模型(即式(3))描述土體的變形，假定滲流符合Darcy定律，且滲透系數kv為常數。

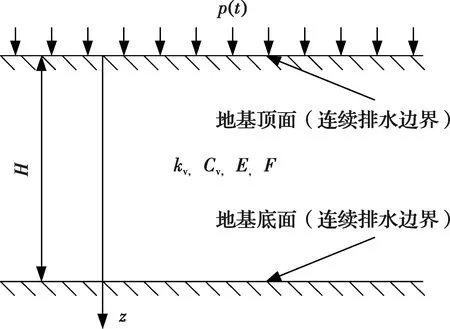
圖2 土體固結模型示意圖

根據有效應力原理可得土體的有效應力為

σ′(z,t)=p(t)-u(z,t)

(4)

式中：u(z,t)為超孔隙水壓力。

土體的一維固結微分方程可表示為

(5)

式中：γw為水的容重。

將式(4)代入式(5)進行Laplace變換可得

(6)

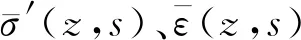
(7)

聯合式(6)、式(7)可得流變固結方程

(8)

式中：Cv=kvE/γw，為固結系數。

式(8)的初始條件以及邊界條件為

式中：b、c為透水性影響因子，可通過試驗模擬或工程實測反演得出。當b、c趨于無窮大時，即為完全透水邊界，當b、c趨于0時，即為不透水邊界。

將式(9)代入式(8)，可化簡為

(12)

式中：β=s/[Cv(Fαsα+1)]。對于定解條件式(12)，可設解的形式為

(13)

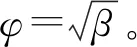
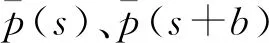
將式(14)、式(15)代入式(13)可得任意載荷下有效應力的通解

(16)

連續排水邊界下分數階黏彈性一維流變固結理論沉降量計算為

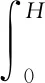
(17)

將式(17)進行Laplace變換可得

(18)

將式(7)代入式(18)可得

(19)

方程(19)即是所要計算的沉降變形。

3 算例驗證及參數分析

對于數值Laplace逆變換，目前,已提出多種反演方法，經過對比分析，采用Durbin[22]基于Fourier級數展開的Laplace數值逆變換求解式

(20)

式中：a、T1(T1>tmax)為求解參數；tmax為最大計算時間；N為級數截取項數；i為虛數單位。

3.1 算例驗證

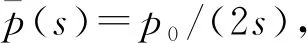
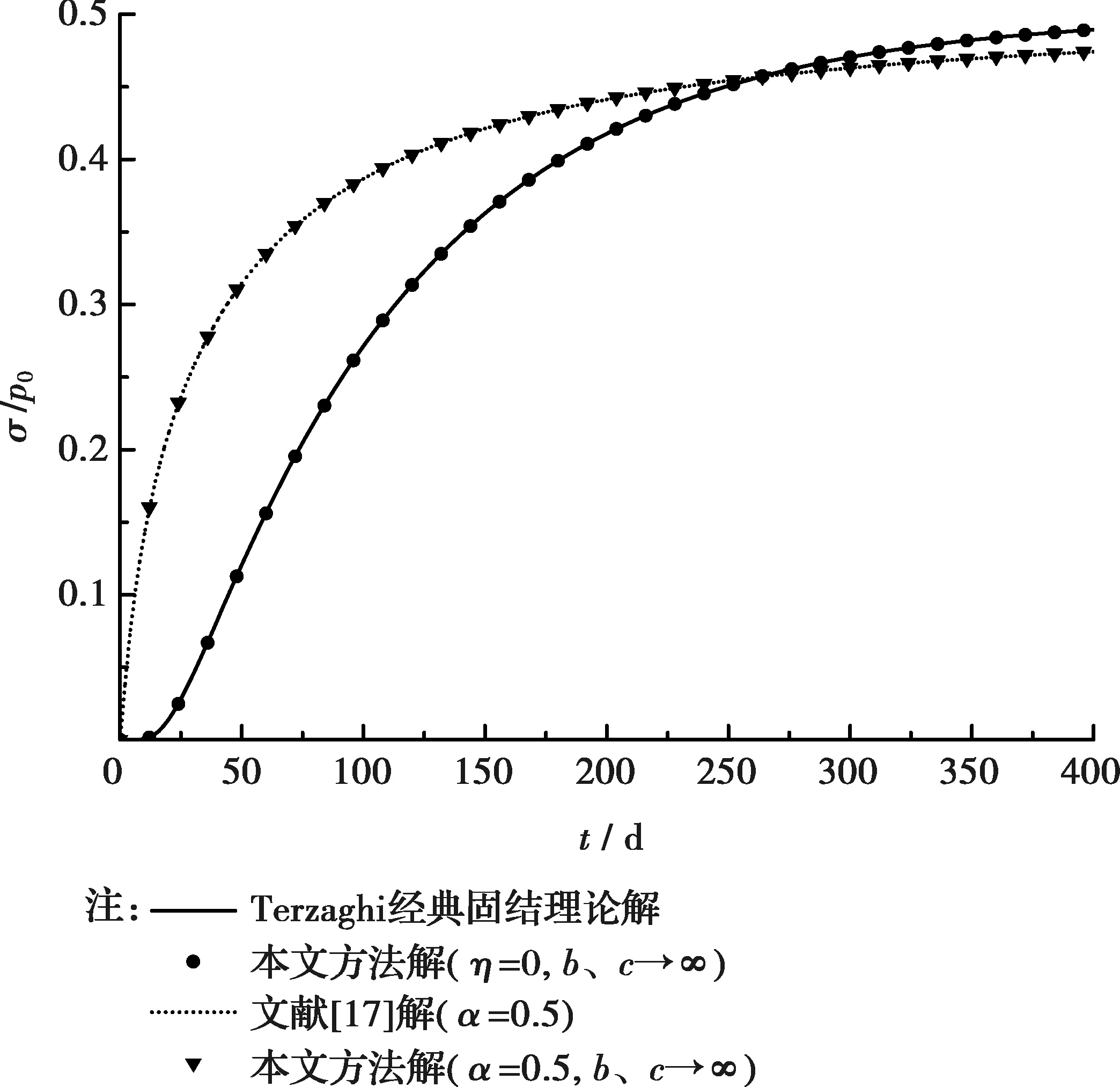
圖3 z=2.5 m處有效應力比隨時間的變化

3.2 參數分析

為進一步考察推導出的任意荷載下連續排水邊界分數階導數黏彈性地基固結沉降解的適用性，并分析相關參數對其固結沉降的影響，采用上述算例中的土體力學參數，以常見的梯形循環荷載及施工荷載為例進行討論。

3.2.1 梯形循環荷載 梯形循環載荷如圖4所示，其傅里葉級數形式為

(21)

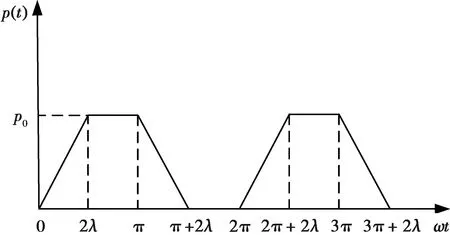
圖4 梯形循環荷載

將式(21)進行Laplace變換可得

(22)

式中：ω=π/T，T為循環荷載的半周期；λ為梯形循環載荷的加載系數，0<λ≤π/2。當λ→0時可退化為矩形循環載荷，當λ=π/2時可退化為三角形循環載荷。將式(22)代入式(19)即可得到梯形循環荷載下連續排水邊界分數階導數黏彈性地基一維固結沉降解。取分數階次α=0.1、p0=1 MPa，半周期T=40 d，加載系數λ=π/4。

1)透水性影響因子b、c

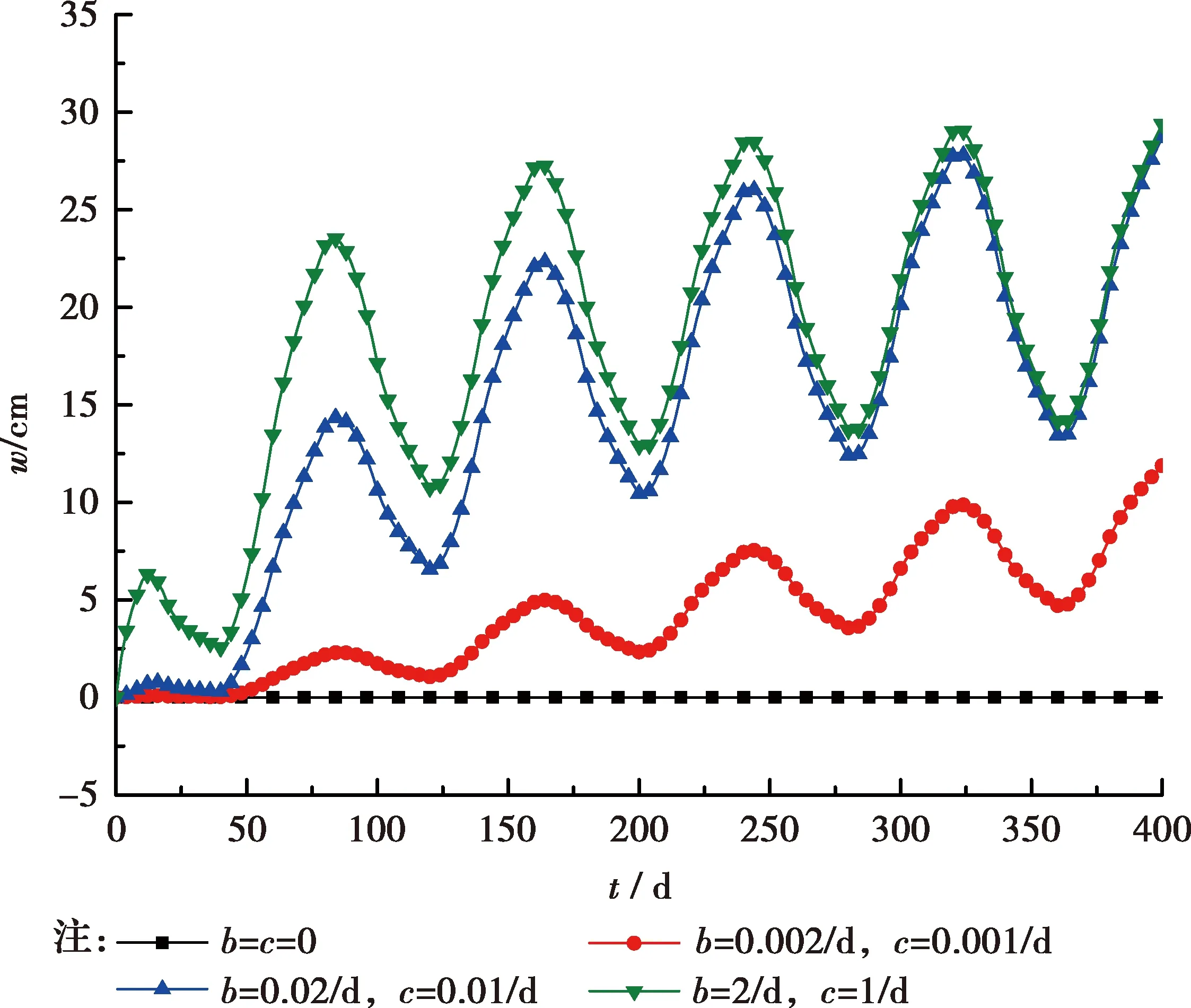
圖5 不同b和c時沉降變化曲線(α=0.1)

圖5為梯形循環載荷下b、c取不同值時對黏彈性地基固結沉降的影響。由圖5可知，當b、c都等于0時，土層上下邊界都不排水，外荷載全部轉化為孔隙水壓力，固結沉降量恒為0；在循環荷載作用下，地基沉降呈振蕩增長，但并非隨荷載的變化同時發生，而是滯后于循環荷載的變化；影響因子b、c越大時，即邊界透水性越好時，固結沉降速率越快，沉降達到穩定的時間越短，并且其振蕩幅值隨著b、c的增大而增大。實際工程中，針對不同邊界透水性的工況可以通過調整參數b和c來近似模擬實際土層的非對稱排水固結特性。

2)分數階次α

透水性影響因子b=0.03/d、c=0.02/d時，不同分數階次α對固結沉降的影響如圖6所示。α描述了材料的多種流動狀態性質，具有一定的物理意義[16]。從圖6可以看出，當其他參數不變時，α越大，固結沉降發展速率越慢，但隨著時間延長，情況則正好相反，即α越小，固結沉降越慢，這與文獻[17]恒載條件下的規律一致。由此可見，最終固結沉降達到穩定的時間隨著α的增大而縮短。另外，隨著分數階次α的增大，理論沉降曲線的振蕩幅值明顯減小，土體對外加荷載變化的敏感程度減小。

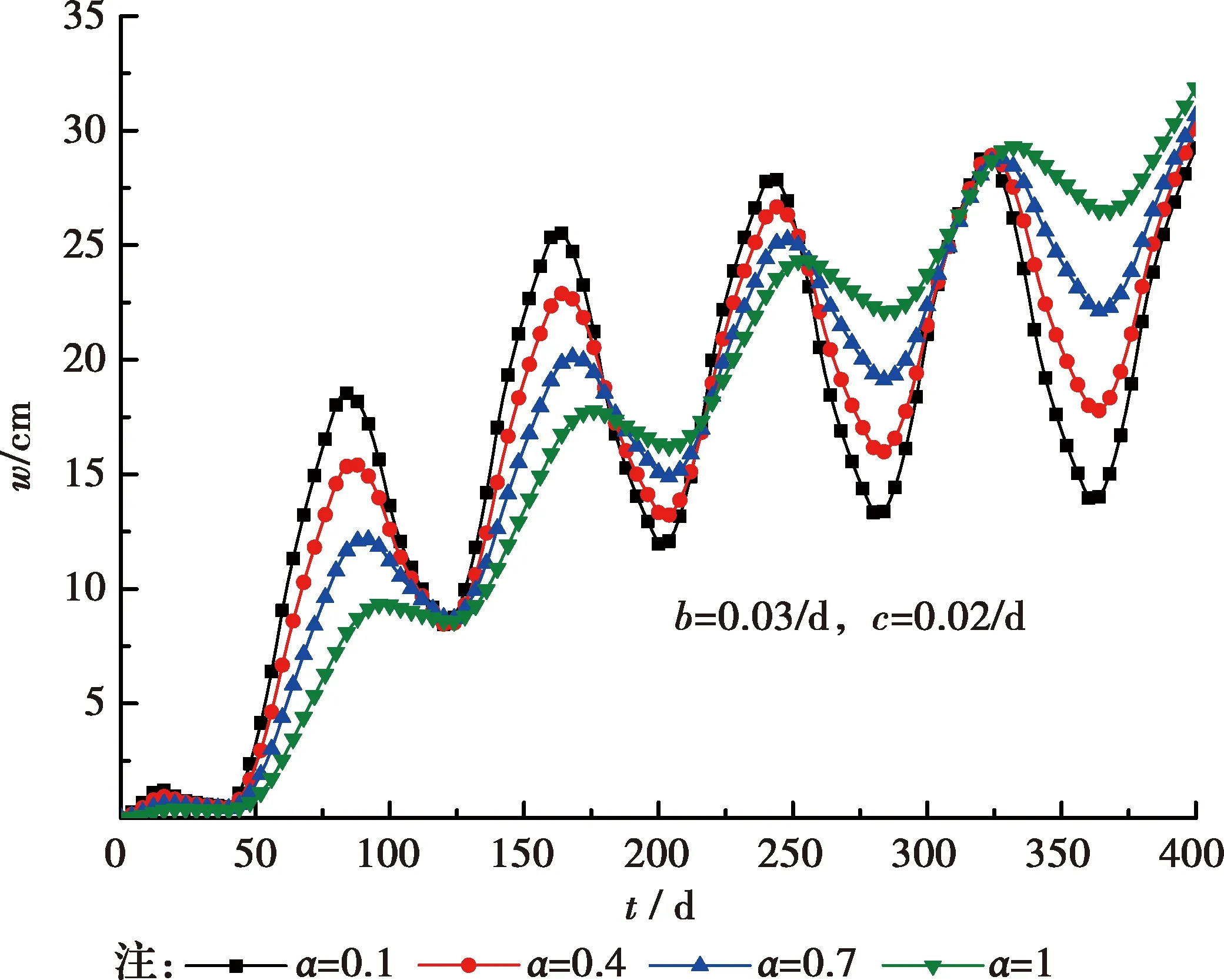
圖6 不同分數階次α的沉降變化曲線

3)半周期T及加載系數λ

圖7、圖8分別為透水性影響因子b=0.03/d、c=0.02/d時，梯形循環荷載的半周期T及加載系數λ對固結沉降的影響，λ=π/2時，即為三角形循環載荷。分析圖7可知，梯形循環荷載的周期越大，分數階黏彈性飽和土體一維固結沉降發展變化越明顯，振蕩幅值越大。從圖8可以看出，加載系數λ越大，即梯形荷載加載階段速率越慢，在固結初期，其沉降量反而越大，隨著時間的延長，加載系數λ越大，沉降發展速率越慢，波動性也越小。

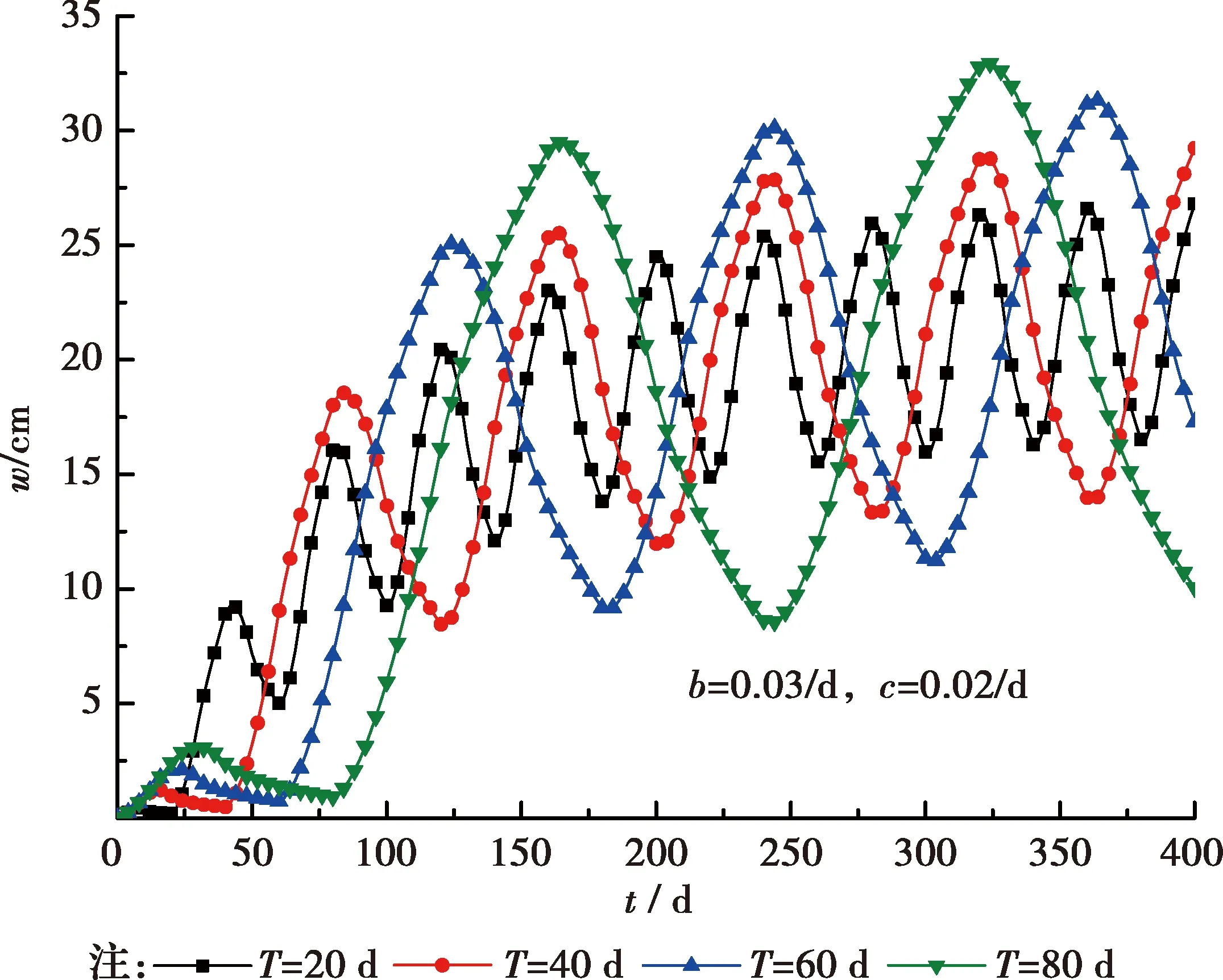
圖7 不同半周期T的沉降變化曲線(α=0.1)

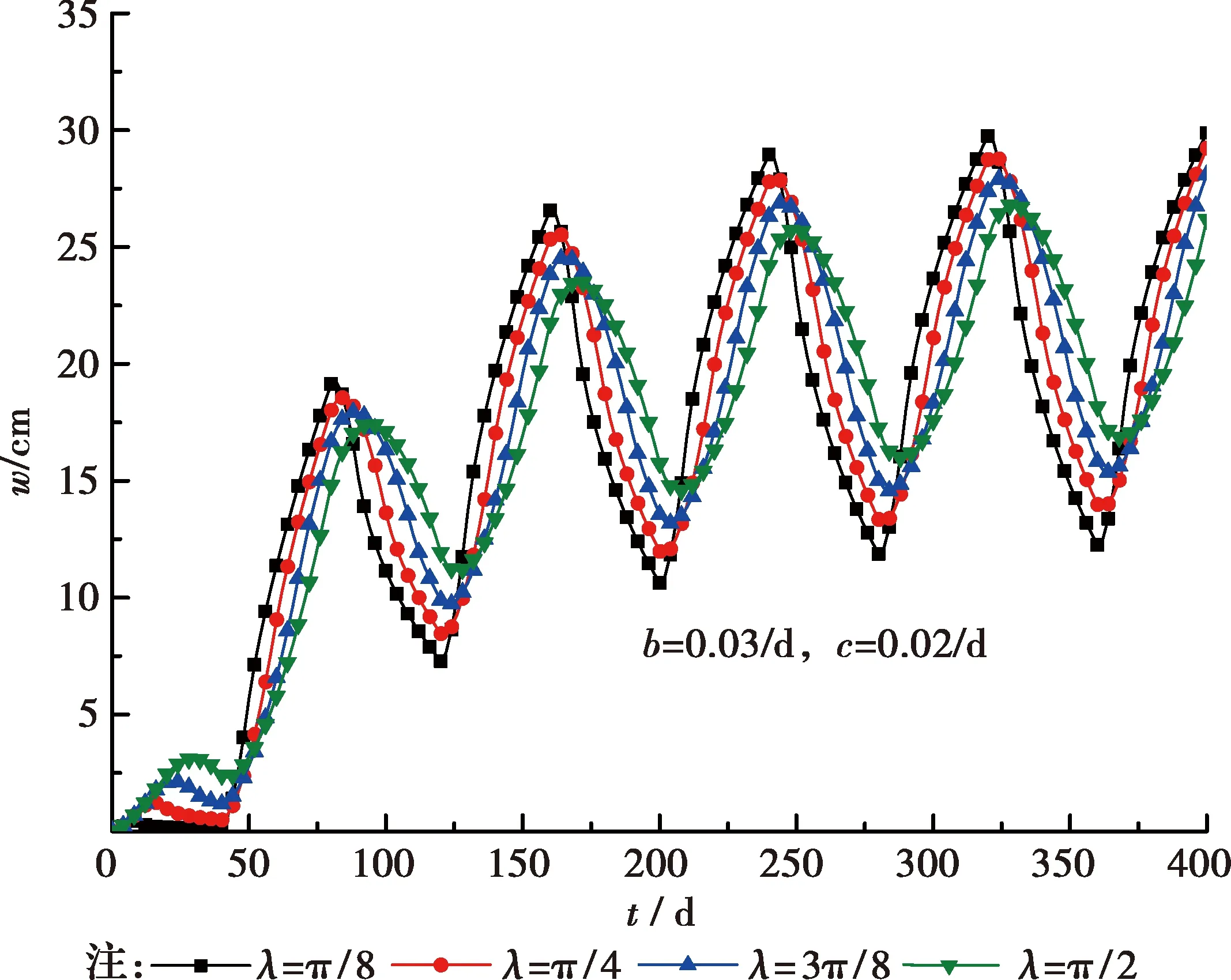
圖8 不同加載系數λ的沉降變化曲線(α=0.1)

4)彈性模量E及黏彈性體的延遲時間F

考察土體力學參數彈性模量E及黏彈性體的延遲時間F對固結沉降的影響，結果如圖9、圖10所示。分析圖9可知，由于彈性模量直接影響土體的壓縮性，彈性模量越大，土體越難被壓縮，最終沉降量越小，固結沉降達到穩定的時間越短，圖中體現為隨著彈性模量E的增大沉降變化曲線越來越早的趨于穩定波動狀態。此外，彈性模量E越大，循環荷載下固結沉降的振蕩幅值越小。從圖10可以看出，由于邊界透水性較差，當其他土體參數不變時，黏彈性體的延遲時間F對固結沉降的影響主要體現在固結中、后期，黏彈性體的延遲時間F越大，即黏滯系數η越大，固結沉降速率越慢，循環荷載下分數階黏彈性飽和土體達到最終沉降穩定所需的時間越長。

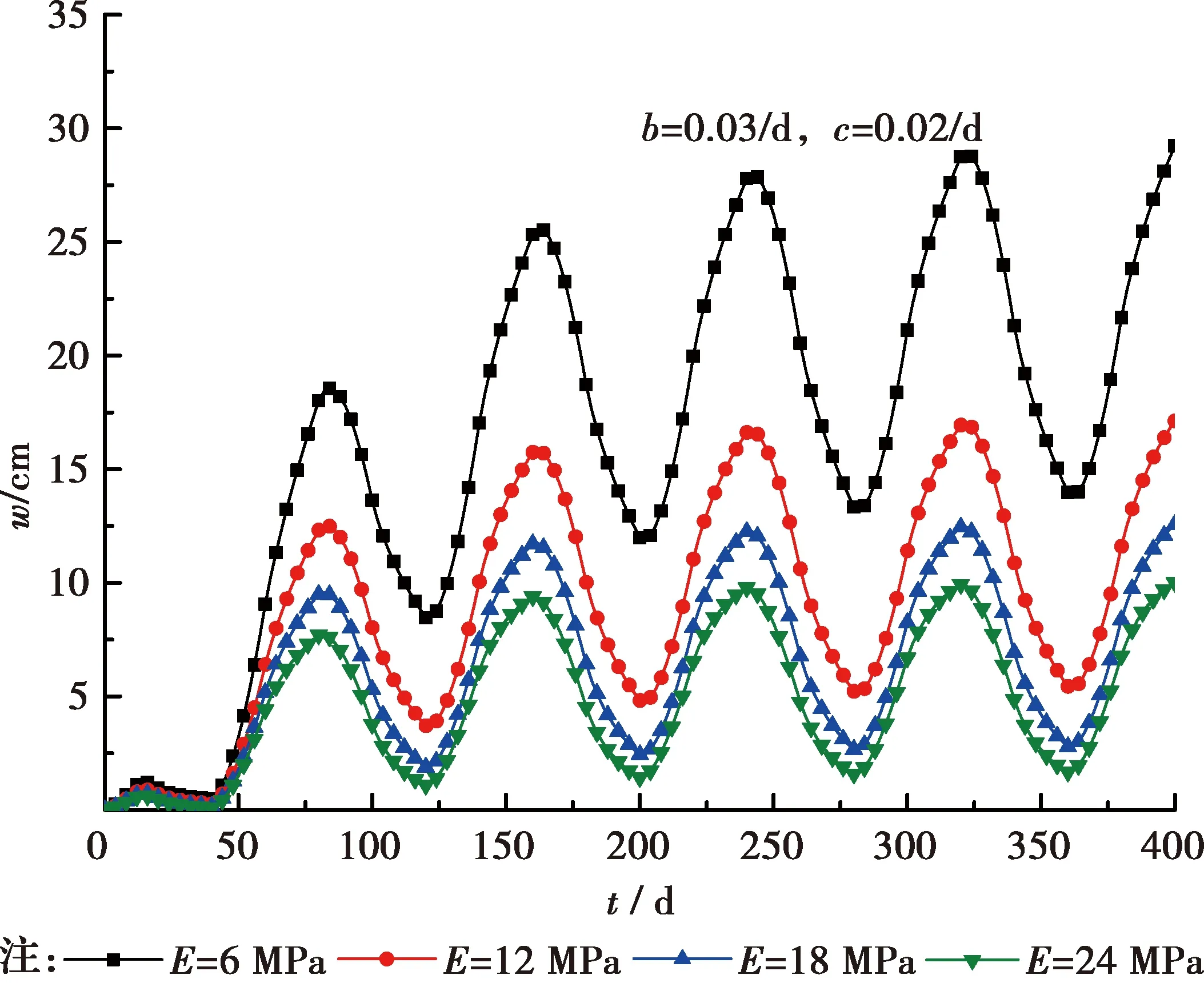
圖9 不同彈性模量E的沉降變化曲線(α=0.1)

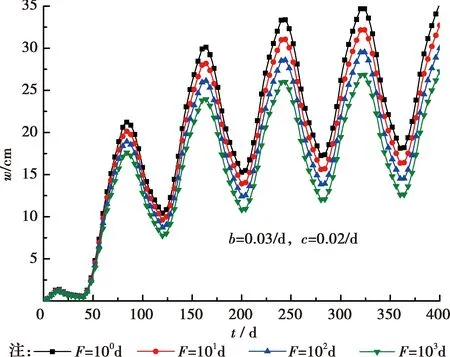
圖10 不同黏彈性體的延遲時間F的沉降變化曲線(α=0.1)

3.2.2 施工荷載 如圖11所示，施工荷載形式可表示為

(23)

式中：D為施工期加載時間。

對式(23)作Laplace變換得

(24)

圖11 施工荷載

取b=0.03/d，c=0.02/d，p0=1 MPa，分析施工荷載下分數階次α及施工期加載時間D對固結沉降的影響，如圖12、圖13所示。

由圖12可知，在固結前期，施工荷載下分數階黏彈性地基固結沉降的發展速率隨著α的增大而減慢，而在固結后期，α增大使固結沉降增長加快，達到最終沉降量的時間減短。從圖13可以看出，其他參數不變時，施工期加載時間D越大，即施工速率越慢，固結沉降變化越慢，但由于最終荷載不變，施工期結束后，沉降變化曲線最終一致。

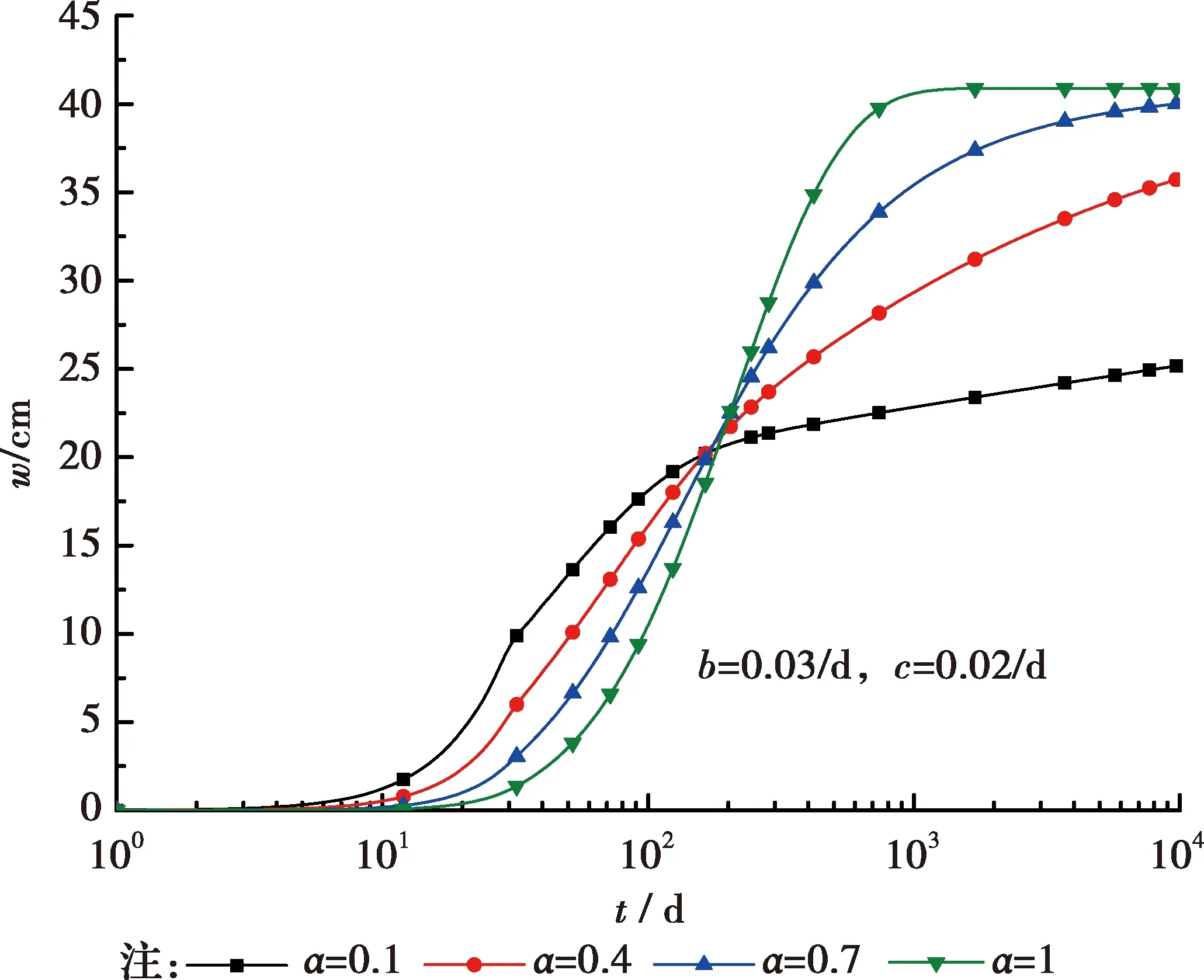
圖12 不同分數階次α的沉降變化曲線(D=30 d)

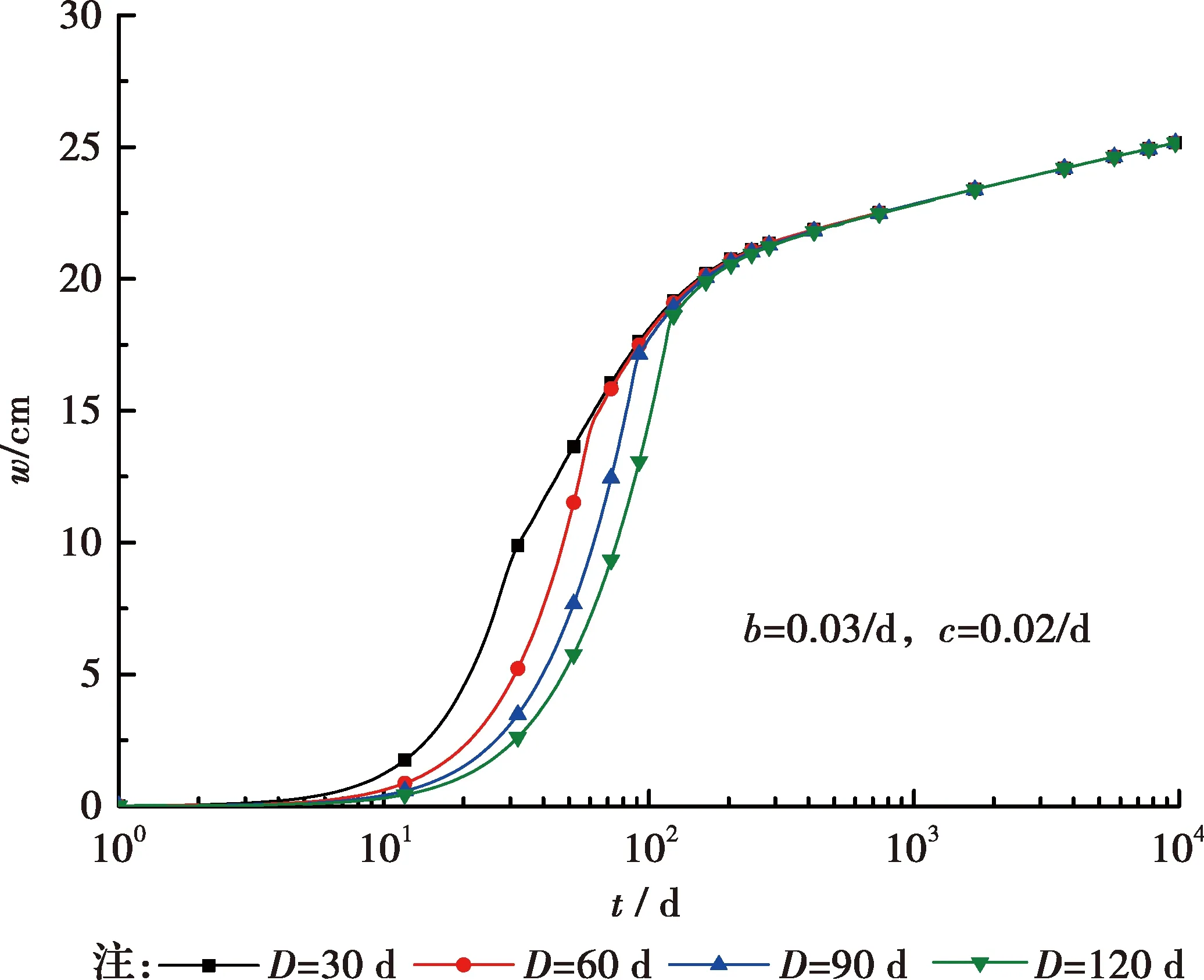
圖13 不同施工期加載時間D的沉降變化曲線(α=0.1)

4 結 論

基于Caputo分數階導數的彈壺元件修正Kelvin模型，引入連續排水邊界條件，利用Laplace變換求得考慮連續排水邊界條件時分數階導數黏彈性地基在任意隨時間變化的荷載下有效應力及沉降的解析解，運用Laplace逆變換得到其時域內的數值解。通過系統的算例分析，可以得到如下結論：

1)循環荷載作用下，黏土地基的沉降變化呈振蕩增長，但滯后于荷載的變化，且振蕩幅值隨著邊界透水性的增大而增大。

2)分數階次α增大，使固結前期沉降發展速率減慢，但在固結后期，α值對沉降的影響正好相反，最終固結沉降達到穩定的時間隨著α的增大而縮短。另外，隨著分數階次α的增大，循環荷載下沉降變化曲線的振蕩幅值明顯減小。

3)分數階黏彈性地基一維固結沉降的發展還與土體力學參數及荷載參數相關。彈性模量E越大，最終沉降量越小，固結沉降達到穩定的時間越短，且循環荷載下固結沉降的振蕩幅值越小；黏彈性體的延遲時間F越大，固結沉降變化速率越慢。