基于云平臺的Lorenz混沌數值模擬實驗
黃六霞,程敏熙,林奇川
(華南師范大學 物理與電信工程學院,廣東 廣州 510006)
“計算機數值模擬實驗”是高校近代物理實驗課程的重要模塊[1]. 實驗要求學生在實驗室使用安裝有C語言的運行程序、配置有相應的運行環境的計算機進行單機實驗. 鑒于C語言語法較復雜、實驗環境不易維護、實驗場所固定等問題,本文將云平臺與教學需要相結合,采用語法簡明、易于上手的Python語言實現數值模擬,在平臺上設置交互(輸入參量、輸出圖像),實現線上修改、編輯和運行代碼的功能,用任意移動終端通過瀏覽器就能訪問云平臺,學習數值模擬和繪制實驗圖像,不受時空和設備的局限,增強學習的自主性,減少人力物力的耗費.
云計算平臺提供了安全、快速、便捷、數據存儲和網絡計算的服務模式,用戶無需硬件設備投入和技術管理人員,無需購買單機版軟件,只需按月支付一定的服務費,即可通過互聯網以按需、易擴展的方式獲得系統平臺或程序軟件等資源,并能通過云計算平臺開發實驗數據處理、數值模擬計算、資源存儲等功能[2].
本文以Lorenz混沌模型為例,在云平臺上實現模擬計算和繪制圖形,觀察混沌狀態.
1 實驗原理及實現條件
1.1 Python語言及Bokeh作圖庫
Python語言是一種計算機程序設計語言,作為可解釋性語言,具有易學、易讀、易維護的特點[3],語法簡潔高效,自帶豐富的第3方庫和各種模塊,包含解決各種問題的類庫,在數據分析以及數據可視化上有突出表現,只需要很少的代碼量就可以實現強大的功能.
Bokeh是一款功能強大的數據可視化庫,支持繪制散點圖、折線圖、柱狀圖等二維圖形,支持現代化Web瀏覽器,可以快速創建交互式的繪圖,提供優雅簡潔的圖形風格. 本文調用Bokeh庫實現數據可視化,展示Lorenz混沌狀態.
1.2 Lorenz混沌模型簡介
1)Lorenz混沌吸引子
以混沌吸引子的x-z“狀態空間(相空間)”圖像為例,圖像形似蝴蝶的翅膀,以2個環形嵌套,每個環形之外有無窮多層,左右環形之間是連通的回線,所有點的軌跡都不會離開曲面而是螺旋地趨近于中心,稱之為“奇異吸引子”. 洛倫茲方程解的代表點表現出的狀態為點由外向內繞若干圈轉到中心附近后, 將“隨機”地跳到另一環套上繼續向內繞, 再突然跳回原來的環套. 相軌道雖然不會冒出環套的邊界,卻不會自相重復,顯示出無序性. 總之,奇異吸引子是系統總體穩定性與局部不穩定性共同作用的產物[4].
2) 蝴蝶效應(初值敏感性)
氣象學家洛倫茲計算氣象模型時,在試圖探究方程解隨時間變化的長期行為過程中,偶然間發現了如果初值相差微小,得到的結果只有一小段與之前重復,隨后會發生越來越大的偏差,這不是計算機的故障,是方程對初值高度敏感的表現. 隨后在一場報告中稱這種現象為“蝴蝶效應”,意思是:在南半球巴西的1只蝴蝶煽動翅膀,一段時間后有可能在美國德克薩斯引發一場龍卷風. 這印證了盡管氣象變化多端,但遵循經典力學規律,也就是說只要設定必要的初始數據,便可以通過計算揭示出氣象規律,讓天氣或者氣象具有可預報性[5].
3)倍周期運動
在Lorenz混沌系統中,盡管方程反映的是非線性的混沌系統,但是實驗表明,在某些條件下,會得到周期性的相空間軌跡.
1.3 Lorenz吸引子的模擬計算
動力學理論用確定的微分方程或離散變量的映射來建立模型,在一定條件下會出現隨機性狀態. 當系統處于既不是完全確定的,又不是完全隨機的形態,表觀的隨機性中又蘊含著規律和有序時[4],稱之為“混沌態”(Chaos),混沌態有非線性、初值敏感性、奇怪吸引子、分岔等現象. Lorenz混沌系統是美國氣象學家洛倫茲(Lorenz)提出的第1個表現奇異吸引子的動力學系統. 他定義了三維的常微分方程組,微分方程組描述為
其中,r(t)=r0+r1cos (ωt),其他參量取值為:a=10.0,b=8/3,ω=7.62. 采用四階龍格-庫塔(Runge-Kutta)法求解方程組即可.

xinc1=f(x,y,z,t)dt
xn+1=xn+(xinc1+2*xinc2+2*xinc3+xinc4)/6,
其中,xn為第n個迭代點,dt為時間步長,固定步長值為0.001,根據上式,從初始值x(t=0)=x0,y(t=0)=y0,z(t=0)=z0開始,可以計算各個時間的x,y和z的值.
2 程序編程與數值模擬
2.1 程序編碼展示
1)編碼計算微分方程的部分代碼如下:
def fun X (x, y, z):
f=(a*y - a*x)*dt
return f
def fun Y(x, y, z, r):
f=(r*x-y-x*z)*dt
return f
f=(x*y-b*z)*dt
return f
x, y, z, T = [],[],[],[]
for i in range(DisplayAfter):
t=dt*i + t0
r=r0 + r1*(math. cos(w*t))
xinc1=funX(x0,y0,z0)
yinc1=funY(x0,y0,z0,r)
在語文教學活動中,學生的閱讀能力以及寫作能力的培養一直是教師所頭疼的問題。當今學生在閱讀語文經典文章時,無法找到作者的主體情感,從而與作者產生不了思想共鳴,更了解不到其中的內涵。除此之外,學生在寫作時總是無從下筆。教師利用讀寫結合的教學方式幫助學生在閱讀時積累詞句,逐漸轉化為自己的語言,巧妙地運用到寫作當中去,以此提高學生的寫作興趣,儲備知識,為學生綜合性發展奠定了堅實基礎。
zinc1=funZ(x0,y0,z0)
xinc2=funX(x0+xinc1/2,y0+yinc1/2,z0+zinc1/2)
yinc2=funY(x0+xinc1/2,y0+yinc1/2,z0+zinc1/2,r)
zinc2=funZ(x0+ xinc1/2,y0+yinc1/2,z0+zinc1/2)
xinc3=funX(x0+xinc2/2,y0+yinc2/2,z0+zinc2/2)
yinc3=funY(x0+xinc2/2,y0+yinc2/2,z0+zinc2/2,r)
zinc3=funZ(x0+ xinc2/2,y0+yinc2/2,z0+zinc2/2)
xinc4=funX(x0+xinc3,y0+yinc3,z0+zinc3)
yinc4=funY(x0+xinc3,y0+yinc3,z0+zinc3,r)
zinc4=funZ(x0+xinc3,y0+yinc3,z0+zinc3)
x1=x0+(xinc1+2*xinc2+2*xinc3+xinc4)/6
y1=y0+(yinc1+2*yinc2+2*yinc3+yinc4)/6
z1=z0+(zinc1+2*zinc2+2*zinc3+zinc4)/6
此部分實現了洛倫茲微分方程的求解,即求解出x,y,z的值.
2) 實現數據可視化的部分代碼如下:
p=figure(title="x-t圖(初值x=y=1.z=1.001)",x_axis_label=′x′,y_axis_label=′y′)
p.line(x, z, line_width=1)
show(p)
此部分代碼調用Bokeh方法,將之前計算的結果轉化成為圖像,實現平臺上數據的可視化.
2.2 Lorenz混沌吸引子
學生瀏覽平臺界面,在界面分別輸入x=1,y=1,z=1,r0=26.5,r1=0等各項參量,點擊提交獲取z-x圖,即可獲得Lorenz混沌吸引子圖像(圖1).
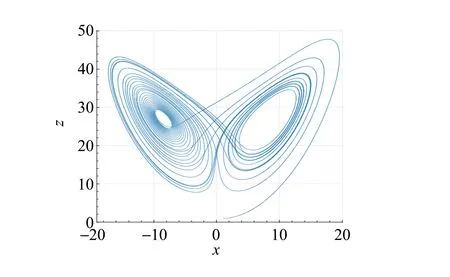
圖1 Lorenz系統的混沌吸引子
2.3 混沌系統對初值的敏感性
平臺上設定不同初值得到不同圖像,即在輸入框中輸入初值時改變z的初值(從1改為1.001,其他條件不變),分別提交獲取不同的圖像(x-t圖、y-x圖、z-y圖、z-x圖),如圖2所示.

(a)x-t圖(x=y=z=1)

(b)x-t圖(x=y=1,z=1.001)
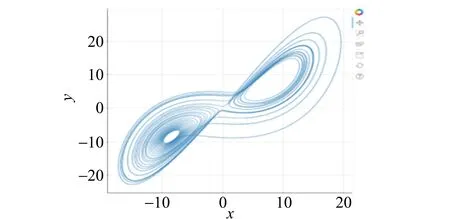
(c)y-x圖(x=y=z=1)

(d)y-x圖(x=y=1,z=1.001)
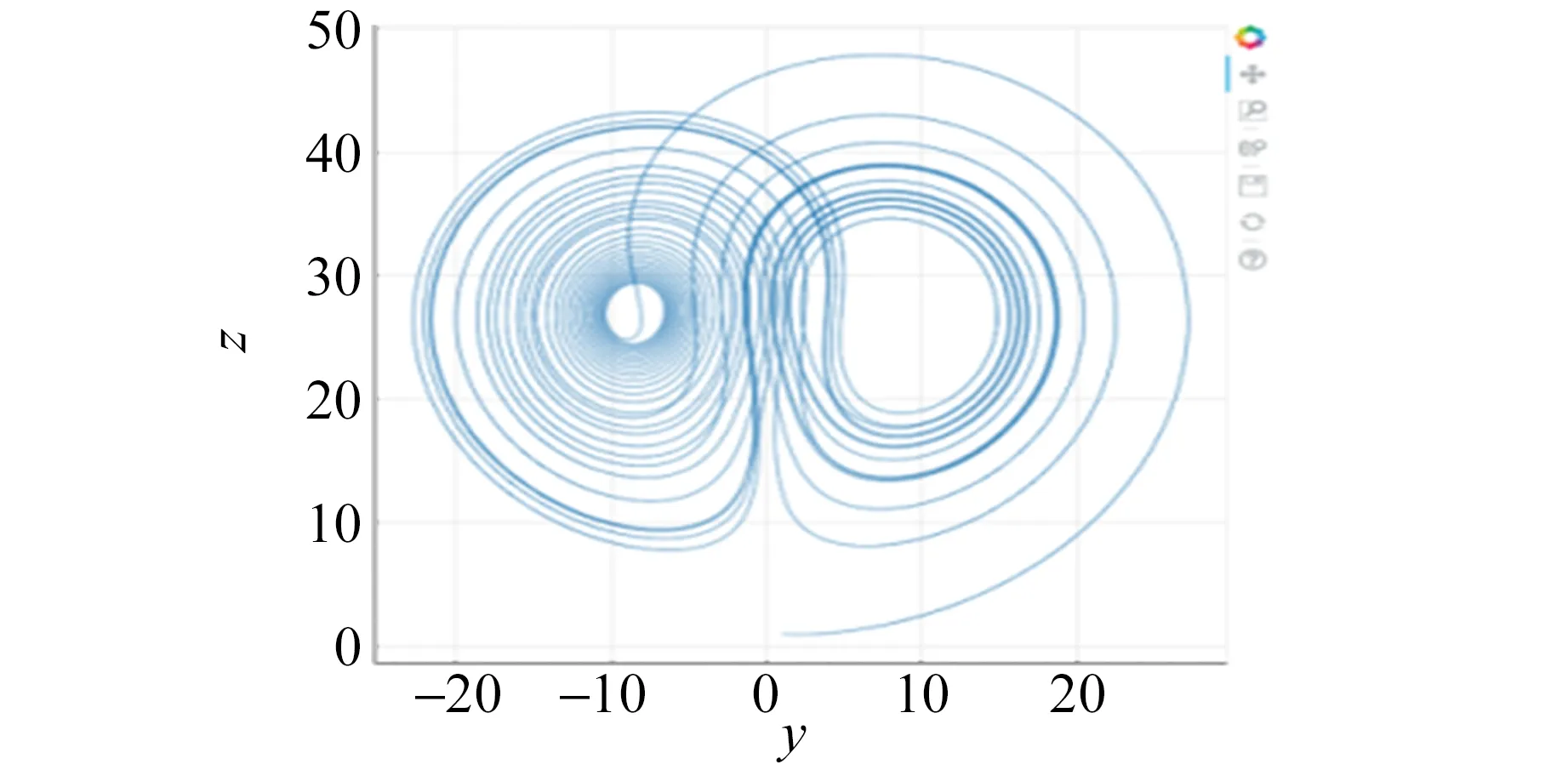
(e)z-y圖(x=y=z=1)

(f)z-y圖(x=y=1,z=1.001)
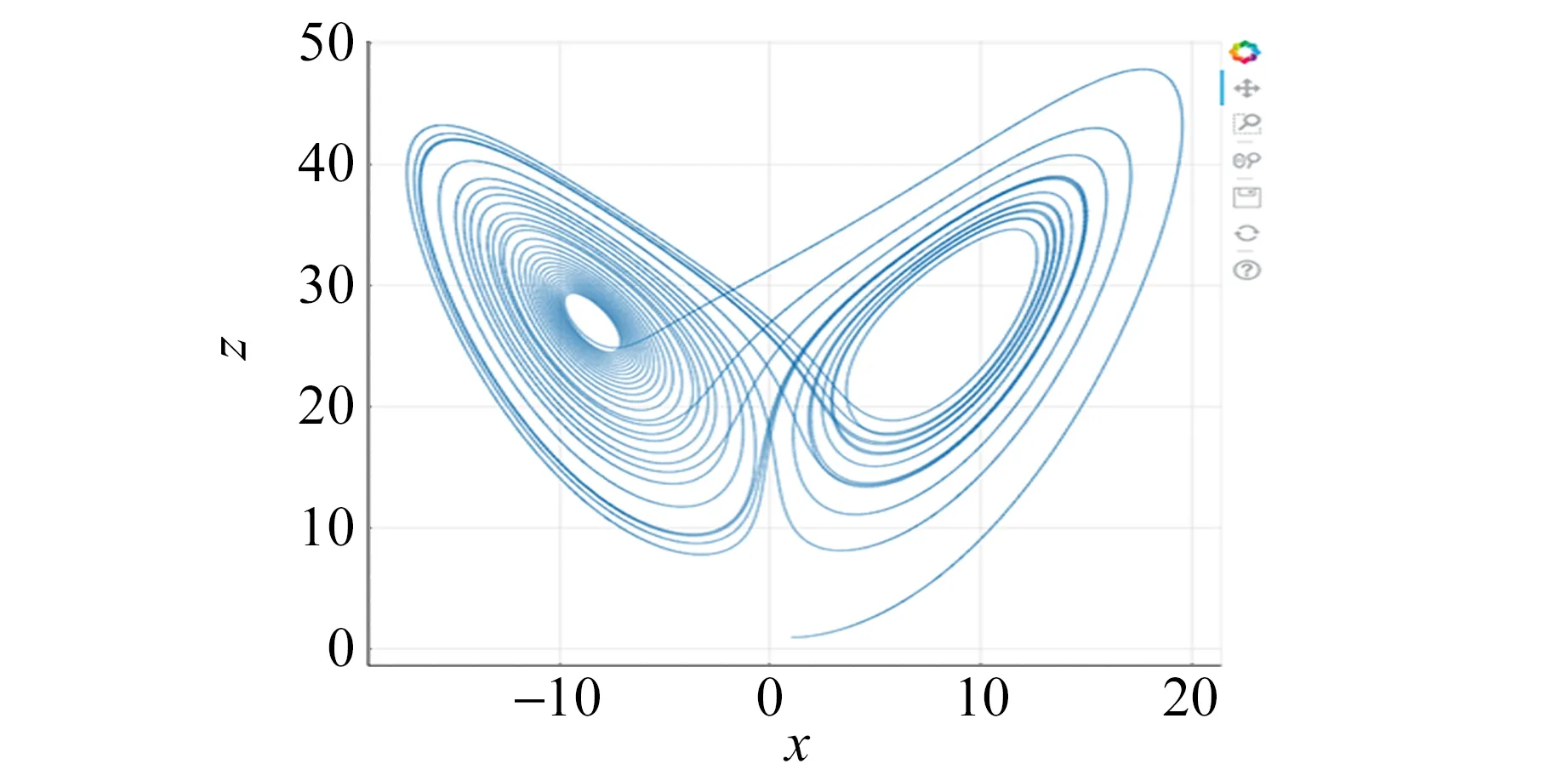
(g)z-x圖(x=y=z=1)
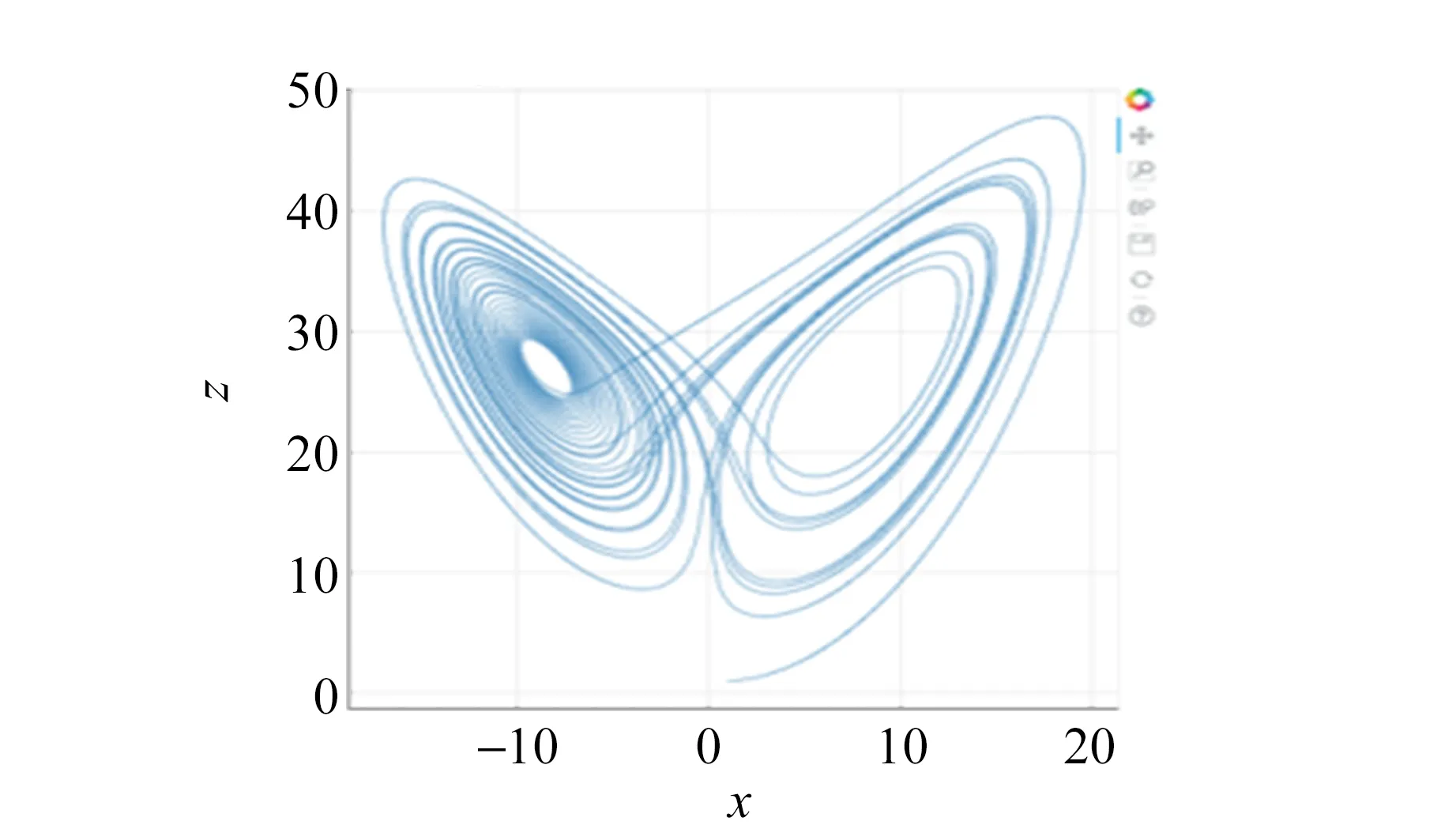
(i)z-x圖(x=y=1,z=1.001)
2.4 混沌系統的倍周期運動
Lorenz混沌系統的倍周期運動是系統在一定條件下處于的穩定狀態,迭代一定次數之后相軌道成為穩定的1條軌道或者幾條軌道. 當輸入的參量r1值從0增大至5,r0=26.5時,系統在經過較長時間(DisplayAfter=50 000)迭代后的狀態會形成穩定的單周期,也可以獲得穩態的雙周期(r0=27.5)、4周期(r0=27.9)、64周期(r0=27.987). 在平臺上輸入相應參量并點擊“倍周期”的按鈕得到圖3,即可驗證混沌系統的倍周期運動.
此外,云平臺的交互界面中設置了“源代碼”按鈕,實現線上獲取代碼資源的功能,以供學習者參考.

(a)單周期

(b)雙周期

(c)4周期

(d)64周期
3 云平臺進行數值模擬實驗的優勢
云平臺實現了線上交互、線上編程2大功能(如圖4所示). “交互界面”可以直接觀察混沌現象,“線上編程”提供了編程實現數值模擬的線上環境,用戶可以通過平臺在線上編輯、修改、運行代碼,達到數值模擬實驗的目的和效果.

圖4 線上編程界面
如表1所示,與傳統單機編程實現數值模擬相比,在教學中利用云平臺進行數值模擬實驗具有較強的優越性. 在實現條件上,本實驗系統在云平臺只需每月支付一定的云服務費,無需單獨配置運行環境,減少教師對機房設備維護和配置的時間;不局限于在計算機上操作、不受時間地域的限制,用戶聯網訪問平臺即能達到數值模擬實驗的目的,完成實驗要求,擴寬了實驗的地域時間范圍;用戶通過線上操作,方便保存和分享實驗結果.

表1 單機實現數值模擬與云平臺的差異
4 結束語
運用Python語言編程實現在云平臺上的混沌現象的數值模擬,程序簡單、容易理解,有助于調動學習者學習的積極性. 區別于在單機上運行C語言的數值模擬方法,云平臺上的操作更簡單,維護更方便. 從單機操作轉變成為線上交互,把實驗室搬到移動終端,實現基于云平臺的數值模擬計算實驗的移動學習.

