基于自適應矩估計方法的光學臨近校正

(廣東工業大學 廣東 廣州 510080)

引言

目前，193 nm浸沒光刻技術[3]一種常見的光刻技術。然而，隨著臨界尺寸(CD)的不斷縮小，在工藝節點上浸沒光刻已經很難滿足當前半導體電路密度的增長的需求[4]。因此，運用分辨率增強技術(RETS)進一步提高光刻系統的圖像精確度一直是該領域研究有效手段。適應矩估計方法(Adam Algorithm，Adam)結合了AdaGrad方法和RMSPro方法的優點，能夠很好地適應梯度變化，能夠自適應調整每次迭代的步長以優化迭代過程。它的主要思想是使用目標函數和約束條件定義或推導出代價函數，然后通過計算代價函數的梯度和選擇合適的更新步長來確定最優化下降方向和大小。

一、矢量模型

光刻投影成像系統主要分為兩個部分：投影光學效果和抗蝕效果。由阿貝成像原理[5]，基于部分相干光照明系統的投影光刻模型在光刻膠中的投影物像強度為[6]

(1)

其中，J(αs,βs)是位于點(αs,βs)處光源的強度，且JSS=∑(αs,βs)J(αs,βs)是所有對成像做出貢獻的點光源強度之和。光刻膠抗蝕作用同樣使用sigmoid激活函數來描述：

(2)

其中，a描述了激活函數的陡峭程度，tr表示激活的閾值。

二、Adam Algorithm算法

文中使用的的自適應矩估計方法Adam Algorithm結合了AdaGrad方法和RMSPro方法的優點，能夠很好地適應梯度變化，自然地對步長進行自適應調整以加速優化過程。

算法流程：

1.計算代價函數(目標函數f(θ))并判斷是否大于λ，若大于λ則進入下一步，反之則退出算法迭代；

2.更新變量:

k=k+1;

gt=θft(θt);(獲得目標函數在t時刻對目標變量的導數)

mt=β1·mt-1+(1-β1)·gt;(更新一階矩陣估計)

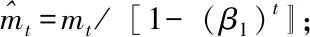
通過簡化上述過程并定義優化變量為φ,對應的在t+1時刻的更新方式可以描述為：

(4)

其中，能量項ε=10-8有兩個作用，一是避免由分母等于0導致的優化無法進行，二是保證優化的順滑性和賦予優化跳出局部最小值的能力。

當我們考慮變量φ的絕對值時，有如下表達式：

(5)

另一種情況下，我們假設算法迭代經過一段時間后，一階矩陣估計累積到了相當大的數值，且變量陷入了局部最小值。此時有t=t1,gt1≈0以及mt,vt?gt，從而可以用下式表示t2時刻的梯度值:

(6)

三、實驗結果分析

本組實驗的正向模型采用基于分層媒介的矢量模型，主要研究的內容是:在相同的照明系統和初始化掩膜下分別使用SGD算法和Adam算法，比較兩種算法的優劣。

我們給出了基于分層模型的SGD和Adam逆優化結果。其中，從左到右分別是照明光源、掩膜和投影物像，從上到下的三組實驗是未優化實驗結果、使用SGD優化的結果和Adam使用優化的結果。在相同條件下觀察兩組實驗我們可以發現使用Adam算法的優化結果更好。

我們給出了SGD和Adam逆優化的代價函數。其中，橫軸代表著算法迭代次數，縱軸代表代價函數的值，紅色曲線和藍色曲線分別代表使用SGD算法和Adam算法的代價函數變化。從結果中可以發現，Adam算法的優化曲線更加順滑，因為它對梯度進行了很好的約束。

四、結論

實驗結果表明，在同等條件下，Adam算法無論是從實驗過程還是優化結果來講均優于SGD算法，這是因為Adam算法能夠很好地適應梯度變化，自然地對步長進行自適應調整以加速優化過程。克服了SGD由于步長小優化速度慢，步長大容易發散的缺點，然而Adam算法更新步長也是在較小范圍內進行搜索，想要進一步提高計算效率就要從提高整體步長入手。