非線性邊界條件的非線性Sobolev方程非常規Hermite元分析
張步英,呂金鳳,孔 亮,鄭俊玲
(河北科技師范學院數學與信息科技學院,河北 秦皇島,066004)
非線性Sobolev方程作為一類重要的數學物理方程,可用于描述多種物理現象,如流體在巖層中的流動、不同介質中的熱傳導過程等[1,2]。關于帶有Dirichlet邊界條件的非線性Sobolev方程已有較多研究成果[3~5]。與Dirichlet邊界條件相比,非線性邊界條件的存在使得連續問題變分形式中增加了邊界項部分,從而,在半離散格式構造時需要考慮邊界項逼近格式設計,這就使得其理論分析較Dirichlet邊界條件的情況更加困難。因此,關于帶有非線性邊界條件的非線性Sobolev方程數值解法的研究成果很少。1992年,Lin等[6]基于真解的非經典Ritz投影,得到了一類帶有非線性邊界條件的非線性Sobolev方程半離散Galerkin格式下逼近解與真解L2模最優誤差估計結果,但關于H1模意義下的逼近情況并未討論。2019年,李先枝[7]采用文獻[8]的方法,結合標準p次矩形元的性質,對一類帶有非線性邊界條件的線性Sobolev方程低階混合元方法的超逼近與超收斂進行了研究。
非常規Hermite元由于其特殊構造及性質[9],受到國內外學者的青睞。該單元已經被應用于多種類型偏微分方程數值解法的研究,如反應-擴散方程[10]、半線性粘彈性方程[11]、非線性拋物積分微分方程[12]等。然而,關于帶有非線性邊界條件的非線性Sobolev方程非常規Hermite元方法的研究至今未見報道。 筆者對一類帶有非線性邊界條件的非線性Sobolev方程非常規Hermite元方法進行研究。其中,第1部分給出了模型問題及其半離散格式;第2部分結合單元構造,對非常規Hermite元的性質進行分析,得到了精細的插值逼近性質;第3部分研究了半離散格式下逼近解與真解的超逼近性質;第4部分利用插值后處理技術得到了逼近解與真解在H1模意義下的整體超收斂結果。
1 模型問題及半離散格式
考慮下述帶有非線性邊界條件的非線性Sobolev方程[6]
(1)
其中,Ω是一個平面有界開區域,?Ω為其光滑邊界。a(u),b(u),c(u),f(u),g(u)及u0(x)均為已知函數,且滿足下述假設條件A*:
(i) 0 (ii)a(u),b(u),c(u)具有有界導函數,并設其具有相同界值,記為K*; (iii)g(u),f(u)滿足Lipschitz連續,并設其具有相同的Lipschitz常數,記為K*。 (1)式的Galerkin變分形式為:求u(·,t)∶(0,T)→H1(Ω), 使得?v∈H1(Ω),有 (2) 其中,(·,·)和〈·,·〉分別表示定義在Ω和?Ω上的函數內積運算符號。 關于非常規Hermite單元的構造參見文獻[9],在此,記相應的有限元空間為 將(2)式的Galerkin逼近格式定義為:求U(·,t)∶(0,T)→Vh,使得對于?v∈Vh,有 (3) 其中,I∶H2(Ω)→Vh表示相應的有限元插值算子。 由文獻[6]可知,半離散逼近問題(3)存在唯一解。 本節結合單元構造特點,得到了一個關于Hermite元的精細插值逼近性質,并由此得到了在超逼近分析中需要的重要引理。 在本節及后續分析中,將定義在Ω和?Ω上的范數分別記作‖·‖s=‖·‖Hs(Ω),‖·‖0=‖·‖L2(Ω),|·|0=|·|L2(?Ω);論證過程中出現的常數C均表示與h無關的正常數,不同的地方表達的值可能有所不同。 采用與文獻[9]類似的方法,可得下述引理2.1成立。 引理2.1設u(·,t),ut(·,t)∈H4(Ω),Iu及Iut分別表示u(·,t)及ut(·,t)在Vh空間中的插值函數,那么,?v∈Vh有 (4) (5) 引理2.2設u(·,t),ut(·,t)∈H4(Ω),a(u),b(u)∈W1,∞(Ω)×(0,T),,則?v∈Vh有 (6) (7) 證明:下面對(6)式進行證明。 類似地,可以證明(7)式的成立性。引理2.2證畢。 由文獻[6]可得如下2個重要結果成立。 (8) 同時,如果v(·,t)∈H1(Ω)且v(·,0)=0,那么 (9) 定理3.1設u和U分別為(2)和(3)的解,u(·,t),ut(·,t)∈L∞((0,T);H4(Ω)),那么 ‖U-Iu‖L∞(H1)+‖Ut-Iu‖L∞(H1)≤Ch3(‖ut‖L∞(H4)+‖u‖L∞(H4)) 證明:?v∈Vh,由格林公式可得 (10) 記θ=U-Iu,w=u-Iu,由(3)式與(10)式作差可得誤差方程為 (11) 在(11)式中令v=θ,并對其兩邊關于t積分,由θ(·,0)=0可得 (12) 下面,對Nt,1≤i≤12進行估計。 由假設A*,插值定理及Cauchy不等式可得 (13) 由引理2.2及Young不等式可得 (14) 由插值定理可得 ‖Iut‖L∞(L2)≤‖ut-Iut‖L∞(L2)+‖ut‖L∞(L2)≤C‖ut‖L∞(H1) (15) 結合假設A*及(15)可得 (16) 類似的 (17) 利用(8)式,得 (18) 同理, (19) 設h充分小,做如下歸納假設 ‖θt‖L∞(L∞)≤1 (20) 那么,由假設A*及(20)式,可得 (21) 類似的 (22) 利用假設A*及(13)~(22)式,可得 利用Gronwall不等式,有 即 ‖θ‖L∞(H1)≤Ch3(‖ut‖L∞(H4)+‖u‖L∞(H4)) (23) 進一步地,令(11)式中v=θt,采用類似的方法可得 ‖θt‖L∞(H1)≤Ch3(‖ut‖L∞(H4)+‖u‖L∞(H4)) (24) 下面,證明歸納假設的成立性。由逆不等式,可得 ‖θt‖L∞(L∞)≤C‖θt‖L∞(H1)h-2≤Ch (25) 也就是說,(25)式左側是h→0時的無窮小量,從而歸納假設是合理可行的。 定理3.1證畢。 (26) (27) (28) 定理4.1在定理3.1的條件下,有 ‖U-u‖L∞(H1)+‖Ut-ut‖L∞(H1)≤Ch3(‖ut‖L∞(H4)+‖u‖L∞(H4)) 證明:由三角不等式、定理3.1及(26)~(28)式,可得 ≤Ch3(‖ut‖L∞(H4)+‖u‖L∞(H4)) 類似地, ‖Ut-ut‖L∞(H1)≤Ch3(‖ut‖L∞(H4)+‖u‖L∞(H4)) 定理4.1證畢。 通過對帶有非線性邊界條件的非線性Sobolev方程非常規Hermite元方法進行探討,得到了半離散格式下逼近解與真解H1模整體超收斂結果。 對于非線性邊界條件,直接在半離散逼近格式中增加了邊界項部分,將其轉化成?Ω上常規非線性項誤差估計進行處理;同時,將半離散問題的初值設計為原問題初值的插值,避免了非經典橢圓投影帶來的計算復雜度。該思路對于帶有非線性邊界條件的發展方程研究具有借鑒價值。關于非常規Hermite元,得到了2個精細的插值逼近性質。結合論證過程可見,這2個性質對于超逼近結果是至關重要的。從而,進一步拓展了非常規Hermite單元的應用范圍。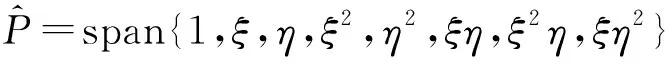
2 相關引理
3 超逼近性分析
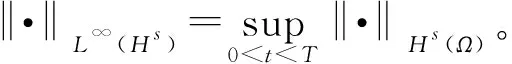
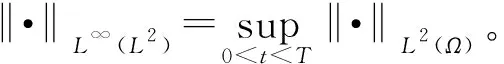

4 超收斂性分析
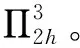
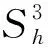
5 結 論

