一類具有分布時滯Emden-Fowler方程的振動性
邸聰娜,滕 博
(河北科技師范學院數學與信息科技學院,河北 秦皇島,066004)
由于Emden-Fowler型微分方程被廣泛地應用于許多重要領域,如核物理學、天體物理、流體力學等,而引起了學者們極大的關注,并且取得了一系列成果[1~7]。
筆者考慮討論一類二階Emden-Fowler型分布時滯微分方程
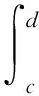
(1)

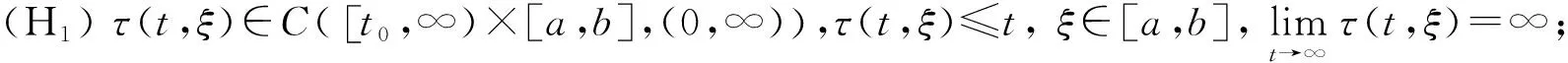
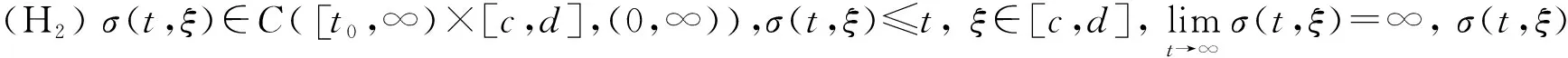

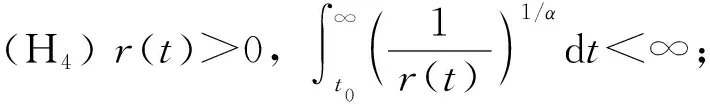
(H5)f(t,u)∈C([t0,∞]×R,R),存在函數q(t,ξ)∈C([t0,∞)×[c,d],(0,∞)),使得|f(t,u)|≥q(t,ξ)|uβ|,β>0。

1 引 理
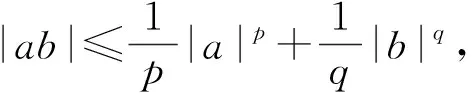
2 主要結果及證明
為了方便起見,引入下列記號
定理2設條件(H1)~(H5)成立,且存在函數φ∈C1([t0,∞),(0,∞)),使得當α≥β時,滿足
(2)
當α<β時,滿足
(3)
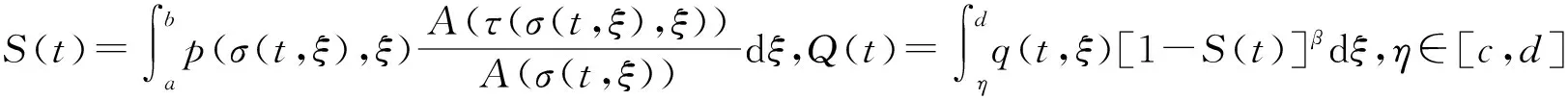
(4)
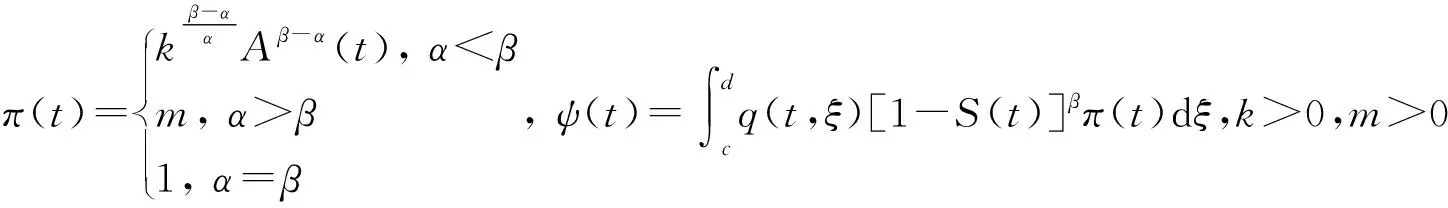
證明反證法。設方程(1)存在一個非振蕩解x(t),不妨設x(t)為最終正解(當x(t)為最終負解時,令y(t)=-x(t),則類似可證),則存在t1≥t0,使得當t≥t1時,x(t)>0,x(τ(t,ξ))>0,x(σ(t,ξ))>0。由函數z(t)的定義有z(t)≥x(t)>0(t≥t1),且由條件(H5)得到
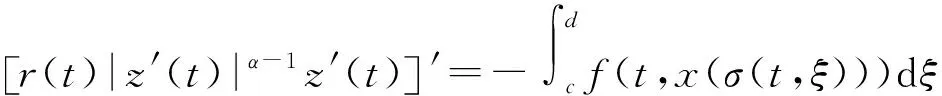
(5)
(5)式說明r(t)|z′(t)|α-1z′(t)嚴格單調減少且最終定號,進而z′(t)也最終定號,所以z′(t)最終為正或最終為負,故只要考慮下列2種情形:
(Ⅰ)z′(t)>0(t≥t1);(Ⅱ)z′(t)<0(t≥t1)。
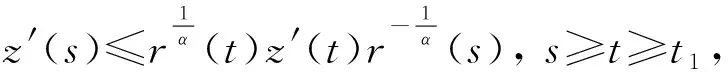
令u→∞,則有
(6)
(7)
另一方面,由函數z(t)的定義,(7)式及x(t)≤z(t)可得
所以
(8)
作Riccati變換
(9)
顯然,w(t)>0(t≥t1)。對(9)式兩邊求導并利用(5)(8)式及r(t)(z′(t))α≤r(σ(t,ξ))(z′(σ(t,ξ)))α,得
(10)
當α≥β時,由于當t≥t1時,z(t)>0,z′(t)>0,所以當t≥t1時
z(σ(t,ξ))≥k1
(11)
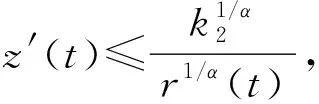
(12)
于是,利用(9)(11)(12)式,由(10)式得
(13)
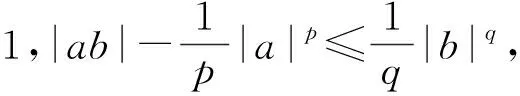
這與(2)式矛盾。
當α<β時,由(10)式,并利用(9)(11)及引理,類似地可得
(14)
兩邊從t1到t積分,得
這與(3)式矛盾。
情形(Ⅱ)z′(t)<0(t≥t1)。因為r(t)|z′(t)|α-1z′(t)=r(t)(-z′(t))α-1z′(t)在[t1,∞)上嚴格單調減少,故r(s)(-z′(s))α-1z′(s)≤r(t)(-z′(t))αz′(t),s≥t≥t1,即z′(s)≤r1/α(t)z′(t)r-1/α(s),s≥t≥t1,同情形(Ⅰ)中的證明,可得到(6)(7)(8)式仍成立。作Riccati變換
(15)
則v(t)<0(t≥t1),由(15)式,并注意到(5)式,則有
(16)
根據(5)式,當s≥t1時,有
r(s)(-z′(s))α-1z′(s)≤r(t1)(-z′(t1))α-1z′(t1)=-k(k>0是常數)

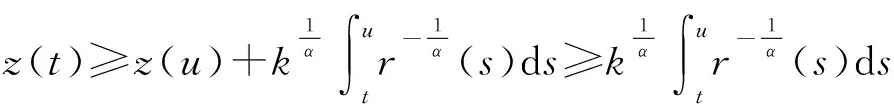

(17)
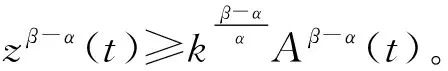
若α>β,由z(t)>0,z′(t)<0(t≥t1)得,z(t)≤z(t1)=M,即zβ-α(t)≥Mβ-α。
若α=β,則zβ-α=1,注意函數π(t)的定義,于是就有
zβ-α(t)≥π(t)
(18)
因為z′(t)<0,故由(8)式可知
(19)
利用ψ(t)的定義,由(18)(19)式可得
=ψ(t)
將之代入(16)式,則有
(20)
(20)式兩邊同乘(t-s)w后積分,得
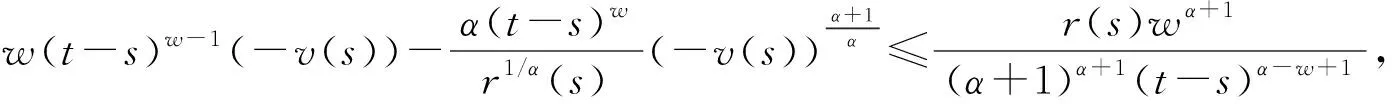
這與條件(4)矛盾。證畢。
3 結 論
具有分布時滯微分方程的振動理論是微分方程振動理論的重要內容。本次研究利用Riccati變換、不等式放縮技巧以及分類討論等方法討論了分布時滯方程(1)在非正則條件下的振動準則,并且去掉了對r′(t)>0的限制。所得結果在豐富了該類方程已有結論的同時,也擴大了該類方程在生物學、經濟學以及物理學等方面的應用范圍。

