混凝土工字梁偏心受壓應力場超聲測試
湯 真
(重慶交通大學,重慶 400074)
0 前 言
20世紀30年代,人們開始研究混凝土無損檢測方法,80年代,美國學者Mary Sansalone利用機械波反射法進行無損檢測,近年來,測試內容也由強度推定、內部缺陷探測等擴展到混凝土結構應力范疇,2012年,宋麗莉等[1]對水泥和巖石樣品開展散射波試驗研究,證明多次散射波形成的尾波比直達波對介質性質變化更為敏感,2018年,黎志謀[2]開展了超聲尾波對混凝土梁三點彎曲應力場超聲測試,利用泰勒展開式,建立了幅值一階變化系數與應力變化近似線性曲線。
本文制定了混凝土工字梁偏心受壓超聲尾波應力測試方案,以奇異值分解為基礎理論,建立了超聲尾波波形的幅值特征向量與混凝土結構荷載等級關系曲線。
1 試驗方案制定
本方案對混凝土工字梁空載及20個荷載的偏心壓力作用下進行超聲測試,設計好荷載取值范圍及施加荷載的具體位置,利用Midas Civil建立試驗加載模型提取出相應的應力計算值,由RSM-SY5(T)型非金屬超聲波檢測儀發射超聲脈沖信號,通過接收多次散射波形成的尾波記錄及保存數據。
1.1 試件設計
本次試驗采用的梁體構件為鋼筋混凝土工字型梁,跨徑2 m,整體梁高45 cm,其中翼緣板寬30 cm,翼緣板高10 cm,腹板寬10 cm,腹板高25 cm。縱向鋼筋和箍筋均采用直徑為10 mm的HPB300級鋼筋。
1.2 超聲測試裝置及加載系統
1.2.1 超聲測試裝置
超聲測試裝置由RSM-SY5(T)型非金屬超聲波檢測儀和換能器組成,平面換能器中心頻率50 kHz,直徑為4 cm,布置方式為一發雙收,換能器布設位置如圖1所示。
1.2.2 試驗加載系統
利用Midas Civil對不同荷載等級下工字型梁體的應力大小進行計算,提取出相應的應力計算值,表1所示。
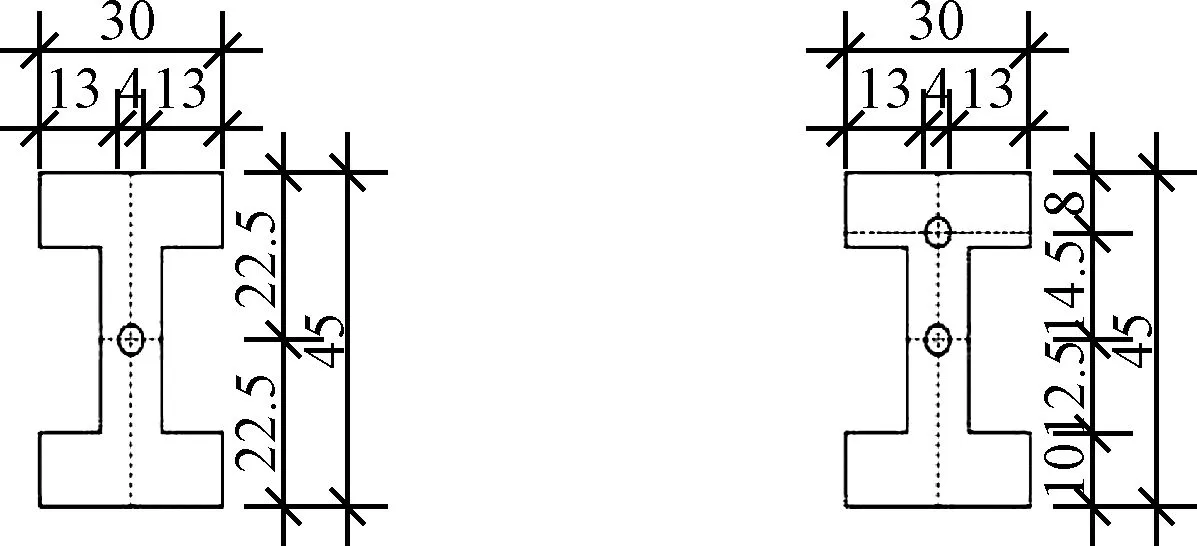
圖1 換能器布設位置示意圖(單位:cm)
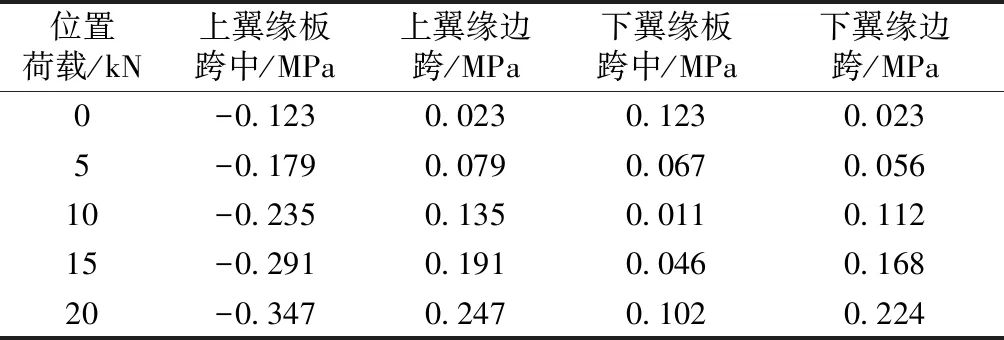
表1 鋼筋混凝土工字型梁部分荷載等級下的應力值
加載方式采用單級加載,采用千斤頂對混凝土工字梁端面施加偏心壓力,千斤頂力作用點距梁體側表面形心軸下方7.5 cm。為保持千斤頂對梁體所施加的壓力不回縮并實時監控施加偏心壓力,在梁體兩側鋼筋貼應變片并配套應變檢測儀,加載系統如圖2所示。

圖2 加載系統示意圖
1.2.3 試驗流程
首先對超聲測試儀器進行30 min左右的預熱,然后利用千斤頂對梁體進行偏心加載。每天進行一次完整混凝土工字梁偏心加載試驗,每次完整試驗共7組超聲測試,每組測試共21個荷載狀態(含自重),荷載范圍(1~20 kN),每一級荷載測試將記錄超聲波形11條,共進行5次完整試驗,如圖3所示。

圖3 現場加載測試示意圖
2 試驗數據處理與分析
由于本試驗有2處接收端,故偏心加載試驗數據可構成7×21×11×1 024×2的五維矩陣,為建立了超聲尾波波形幅值特征向量與荷載等級間關系曲線,在數據分析中以偏心荷載等級為自變量,把數據進行平均處理,原始波形進行奇異值分解,利用SVD矩陣性質建立幅值與荷載等級關系,實現采用幅值特征向量來表征荷載等級的數據處理目標。
2.1 數據預處理
選用任一端一次完整試驗測試數據得到7×21×11×1 024的4維矩陣W′,將一次采集數據進行預處理,物理意義容易理解每一級荷載有一個波形,將W矩陣按11次重復移點測試平均為一次,每一天重復測試8組平均為1組,得到21×1 024的二維矩陣。
由于每次超聲測試采集到的波形能量不盡相同,波形數據不具備可比性,為了使波形數據各類指標位于同一數量級上,對其進行了能量歸一化處理,具體過程如下:一條完整的波形Wj由1 024個點構成,Xj為幅值。
Wj=Wj(x1,x2……x1024)
(1)
波性能量:
(2)
波形能量歸一化處理:
(3)
2.2 基于奇異值分解的數據處理
數據經預處理后得到21×1 024二維矩陣W,矩陣W為實數矩陣,W∈Rm×n,則一定存在正交矩陣U∈Rm×m,正交矩陣V∈Rn×n和對角矩陣Σ∈Rm×n,本文中m=1024,n=21,進行奇異值分解矩陣W可表示為[3]:
W=UΣVT
(4)
Σ可表示如下:
(5)
式中,0為零矩陣;p為min(m,n);σp為矩陣W的奇異值,且σ1≥σ2≥…≥σp≥0。
正交矩陣U與VT滿足:
UHU=Em,m
(6)
(VT)HVT=En,n
(7)
式中,UH、(VT)H分別為U、VT的共軛轉置為Em,m、En,n分別為m階、n階單位矩陣。
為建立不同荷載等級下超聲尾波波形數據特征值與荷載等級間的函數關系,設存在特征向量wx,使其與奇異值分解后矩陣相乘等于W與線性向量[ax+b]相乘可表示為:
wxUΣVT=[ax+b]W
(8)
式(8)左右兩側同時右乘:
wxEm,mEm,nEn,n=[ax+b]W(VT)HΣ-1UH
(9)
2.3 數據處理結果與分析
由于矩陣W′經過多次平均處理,為向工程實際過渡,需要確保數據在組內、組間的穩定性、重復性,下面考察各組內及組間數據結果,逐一進行分析。
1)組內數據結果分析。從組內角度考察各天的測試數據:①單天測試數據構成的11×1 024×7×21 四維數據矩陣;②7 個 11×1 024×21 的三維數據矩陣;③進行能量歸一化處理使得波形數據各類指標位于同一數量級上;④采用基于奇異值分解的數據處理方式求取單組組內 11 條波形各自的幅值特征向量Wx;⑤建立幅值特征向量與荷載等級間的近似線性關系曲線。
基于奇異值分解原理求取不同組數下組內 11 條波形的幅值特征向量,建立了幅值特征向量與荷載等級間線性關系,如圖4所示:
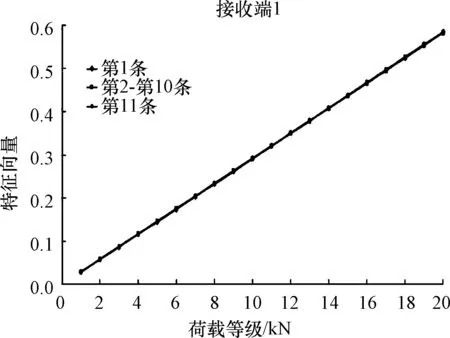
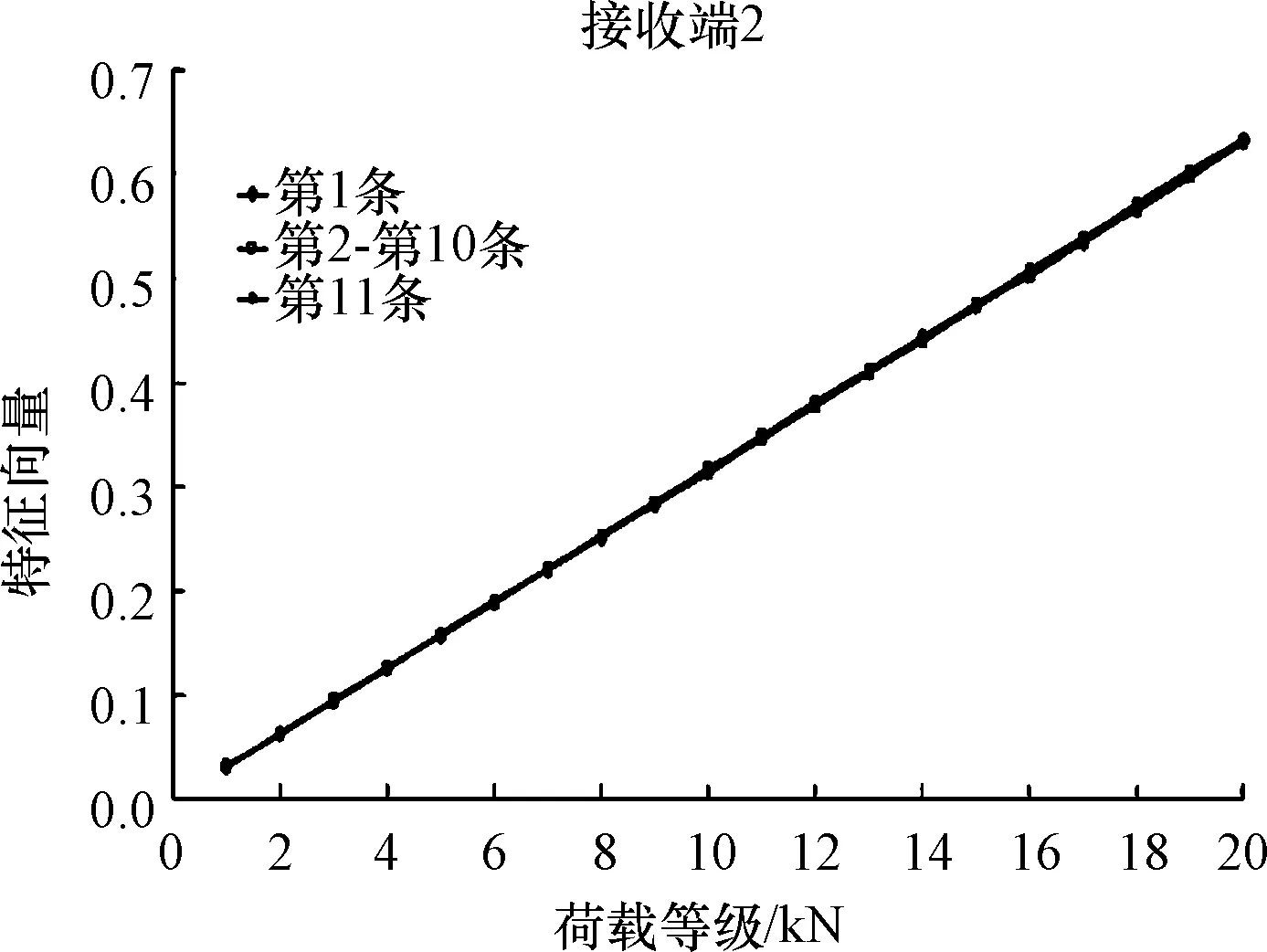
圖4 組內數據特征向量與不同荷載等級間的關系曲線
接收端1、接收端2單組組內11條波形的特征向量Wx與荷載等級間呈現近似線性關系,并且特征向量Wx的離散程度極小。
2)組間數據結果分析。單天測試數據構成的11×1 024×7×21四維數據矩陣按測試組數的不同拆分為7個11×1 024×21的三維數據矩陣,每個三維數據矩陣代表單組測試過程中采集到的波形數據,首先求取11條波形的平均,可將7個三維數據矩陣整合成7個21×1 024的二維矩陣。
進行能量歸一化處理使得波形數據各類指標位于同一數量級上,以單天整體測試數據所構成的二維矩陣W作為開展奇異值分解的基準,分別帶入單組測試數據,求解出各組測試數據在不同荷載等級下的特征向量,建立不同組數據的幅值特征向量與荷載等級間的近似線性關系曲線,如圖5所示。


圖5 各組特征向量與不同荷載等級間的關系曲線
接收端各組測試數據任然存在特征向量Wx與荷載等級間近似線性關系曲線,但同一荷載等級下各組測試數據的特征向量Wx上下位置隨機分布,未出現按加載測試先后順序分布。剔除第一組(黑色線),其余六組測試數據的特征向量Wx間離散程度較小,能達到利用特征向量Wx來識別荷載等級的數據處理目標。
第一組測試數據特征向量Wx明顯偏離于其余六組,主要考慮兩方面,①儀器設備考慮預熱及梁體本身對荷載反應過程記憶了之前的受力歷史擁有了“凱撒效應”;②耦合劑與梁體耦合狀態穩定時間。
3 結 論
對偏心受壓應力場下構件及混凝土梁開展了超聲尾波試驗,基于奇異值分解后的超聲尾波波形幅值特征向量來表征偏心荷載等級的結構測試模型,建立了超聲尾波波形幅值特征向量與荷載等級間的近似線性關系曲線。
從組內的角度對單天測試數據展開處理及分析,單組組內 11條波形數據的幅值特征向量與荷載等級間呈現出近似線性關系,并且不同荷載等級下單組組內 11 條波形數據的幅值特征向量離散程度極小;從組間的角度對單天測試數據展開處理及分析,線性關系明顯,雖然不同組的波形幅值特征向量間出現了隨機的偏移,但識別荷載等級仍然有效。
[ID:009085]

