基于改進四參數嚴密平差法的高鐵CPⅢ相鄰區段搭接處理方法研究

蔣英豪，張獻州, 2，陳旭升，夏晨翕，陳霄

基于改進四參數嚴密平差法的高鐵CPⅢ相鄰區段搭接處理方法研究

蔣英豪1，張獻州1, 2，陳旭升1，夏晨翕1，陳霄1

(1. 西南交通大學 地球科學與環境工程學院，四川 成都 611756；2. 高速鐵路運營安全空間信息技術國家地方聯合工程實驗室，四川 成都 611756)

高速鐵路軌道控制網(CPⅢ)主要為軌道鋪設、精調及運營維護提供安全、穩定、可靠的控制基準。針對軌道控制網相鄰區段的搭接精度會直接影響軌道平順性的問題。基于假設檢驗理論，運用坐標差異性檢驗法對相鄰搭接區段重疊點的獨立平差坐標進行處理，得到重疊點坐標的差異性參數，以便科學合理地選擇搭接點。分析經典四參數轉換法的不足，并對經典四參數轉化法進行優化，以此為據，比較分析經典四參數轉換法和余弦函數平滑法的優劣，提出基于四參數轉換的嚴密平差搭接法。結合具體工程實例，對3種搭接方法進行對比分析。研究結果表明：新的搭接處理方法可以有效改善軌道控制網搭接精度。

區段搭接；差異性檢驗；改進四參數轉換法；嚴密平差搭接

高速鐵路CPⅢ控制網是軌道鋪設、精調及運營維護的基準，高精度的CPⅢ控制網是實現軌道高平順性的前提[1]。對于運營期的高速鐵路，天窗時間較短，CPⅢ平面控制網根據施測計劃分段進行測量，各區段的觀測數據存在測量誤差，會導致區段之間重疊點的坐標不一致。為了保證軌道的平順性，必須做好相鄰區段的CPⅢ銜接工作，而相鄰區段CPⅢ控制網的銜接主要采用搭接處理。目前，我國在建和運營的高速鐵路CPⅢ控制網區段搭接主要采用嚴密平差法[1]，此外還有余弦函數平滑 法[2]和四參數轉換法[3]等。由于嚴密平差法容易造成搭接區段誤差累積，嚴重時會影響軌道的平順性[4]。因此，本文在嚴密平差的基礎上，結合四參數轉換法提出更為合理的搭接方法，通過理論分析和實測數據驗算，證實了該方法可以有效改善軌道控制網相鄰區段的搭接精度。

1 搭接區段重疊點差異性檢驗

目前，《高速鐵路工程測量規范》中明確規定，在選取搭接點對時，前后區段獨立平差重疊點坐標較差≤3 mm，滿足該條件后，選擇1~3對前一區段重疊點作為后一區段的約束點，經嚴密平差得到后區段CPⅢ平面網的坐標成果。但由于工程施工、列車運行震動等外部因素的干擾，以及測量誤差的影響，搭接區段兩次測量的CPⅢ坐標差有可能表現出各向異性，平差計算得到的CPⅢ點精度也不一致，所以直接以重疊點坐標較差作為約束點對選擇的理由不夠充分。搭接處理時使用變形過大的CPⅢ點作為約束條件會給后一區段引入新的誤差，致使最終的計算精度不滿足規范要求。因此，采取某種數學統計檢驗方法分析搭接點2組坐標的差異性是十分必要的。

CPⅢ相鄰區段重疊點的坐標真值無法得到，通過高精度的測量，可以得到外業質量較好的成果，若計算得到的前后區段重疊點坐標估值差異較大，可以認為CPⅢ點位發生了變形；若無明顯差異，則認為前后區段兩次測量的估值結果一致。對于如何認定重疊點是否存在明顯差異，可以利用數理統計中假設性檢驗的相關內容，對重疊點坐標進行差異性檢驗。假設性檢驗的種類較多，針對搭接區段重疊點的相關性質，采用T檢驗的方法對重疊點進行差異性檢驗[5]，獨立樣本的T檢驗用于分析兩組獨立觀測量之間的差異情況，重疊點坐標估值差異性檢驗原理[6]如下。

則檢驗統計量

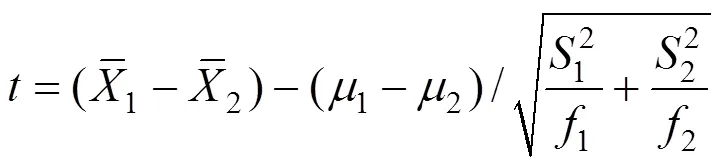
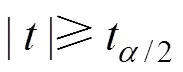
對相鄰搭接區段的CPⅢ分別測量并獨立平差，可以得到重疊點的2套坐標成果。

重疊點平差坐標

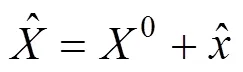
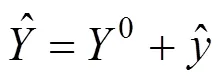
驗后單位權中誤差

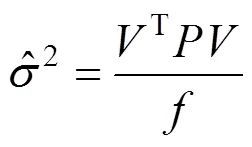
對重疊點坐標平差值的差異性進行檢驗。設前后區段重疊點的坐標較差

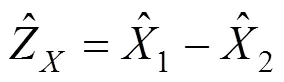
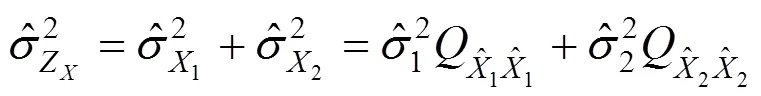
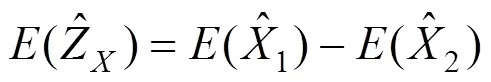
則原假設與備擇假設

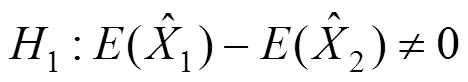
分布的統計量

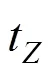
2 CPⅢ相鄰區段搭接方法

2.1 余弦函數平滑法

余弦函數平滑是通過余弦函數處理CPⅢ搭接區段重疊點的兩套坐標，最終得到重疊點唯一坐標，余弦函數平滑搭接示意圖，如圖1所示。

圖1 CPⅢ平面控制網相鄰區段余弦函數平滑搭接原理示意圖

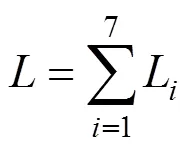
對搭接區段內某一重疊點，設該點在前搭接區段的坐標權比為，則該點在后搭接區段的坐標權比可以表示為1?。余弦函數的權值表達式

式中：為余弦函數振幅；為余弦函數在方向的平移量。

由于和點位于搭接區域外，兩點坐標有唯一值，點處=0，=1，點處=π，=0，可求得平滑函數的具體表達式

通過式(12)可求得重疊點C在前搭接區段的坐標權值，如式(13)。

則重疊點C在后搭接區段的坐標權值為1?p。

通過余弦函數求得重疊點的坐標權值后，可算出搭接區段CPⅢ重疊點坐標的唯一值

同理可得出線路另一側搭接區段內CPⅢ重疊點的唯一坐標。

2.2 四參數法

平面四參數模型廣泛用于獨立坐標系以及工程施工控制網，對CPⅢ相鄰搭接區段而言，將前后搭接區段視為2個剛體，前一搭接區段坐標系統下重疊點坐標視為真值，通過四參數坐標轉換模型，修正后一搭接區段的重疊點坐標值，也就是把2個剛體連接成為一個整體[8]。平面四參數模型基于2個坐標偏移量、一個旋轉參數和一個尺度參數，轉換公式如下[9]：

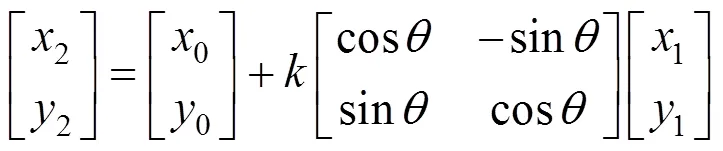
式中：(1,1)為后區段平差坐標；(2,2)為前區段平差坐標；(0,0)為平移參數；為旋轉參數；為尺度參數。

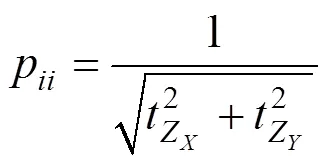
由于系數矩陣由常數項(0,1)和帶有誤差的后區段坐標項兩部分組成，可以考慮采用混合整體最小二乘法[10](LS-TLS)把系數矩陣的常數項從中剔除。針對平面四參數坐標轉換，本文提出一種改進的四參數坐標轉換法，參數迭代解算步驟[11]如下。

將系數矩陣分成1，2

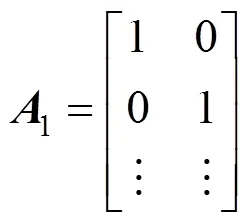
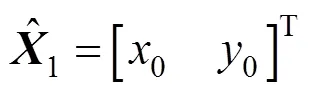
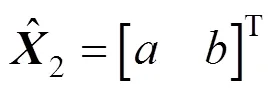
2)設迭代因數

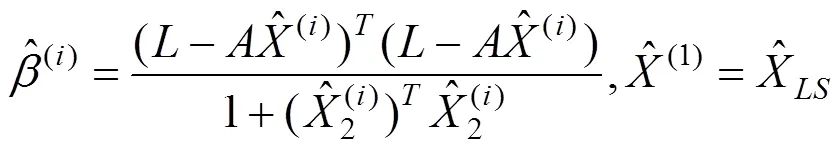
3)則

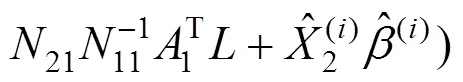
2.3 基于改進四參數轉換的嚴密平差法

經過余弦函數平滑法處理的搭接區段，一定程度上提高了搭接區域內軌道的短波平順性，但對軌道的長波平順性沒有任何改善[12]。若相鄰區段的部分重疊點坐標較差大于3 mm，使用余弦函數平滑法處理重疊點坐標時，會將已經發生變動的CPⅢ點坐標強制賦權平滑，影響軌道控制網相鄰區段的搭接精度。為了改善軌道的長波平順性，減小因重疊點坐標較差較大對CPⅢ網搭接產生的影響，本文提出基于四參數轉換的嚴密平差搭接方法，其原理是：首先選取通過差異性檢驗的所有重疊點作為四參數轉換的基準點對，計算4個轉換參數，然后通過轉換參數計算所有重疊點在前一區段坐標系統下的坐標。最后在6對重疊點中選取1~3對重疊點作為后搭接區段的約束點，經嚴密平差得到后區段CPⅢ網的平差結果。

3 實測數據計算與分析

結合國內某客運專線CPⅢ平面控制網進行搭接處理，對前后區段CPⅢ平面網分別獨立平差，平差后各項指標均滿足規范要求。對前后相鄰區段平差得到的重疊點坐標進行差異性檢驗，選擇T值滿足要求的所有重疊點作為轉換基準點，得到4個轉換參數，并對所有重疊點進行轉換。分別采用嚴密平差搭接法、余弦函數平滑嚴密平差搭接法以及四參數轉換嚴密平差搭接法計算同一搭接區段，其中余弦函數平滑嚴密平差是通過余弦函數法計算出重疊點唯一坐標，再選取1~3對重疊點作為后搭接區段的約束點，最后按照嚴密平差法得到最終坐標成果。為了保證搭接方法的可比性，3種方法選取相同的重疊點作為約束點進行平差。此處選取2組搭接區段CPⅢ數據進行獨立平差，第1組前后搭接區段重疊點坐標較差較大，第2組前后搭接區段重疊點坐標較差較小，重疊點坐標差值及差異性如表1所示。

選擇202713，202714，202719和202720點作為第1組數據搭接處理的約束點，選擇024307，024308，024309和024310點作為第2組數據搭接處理的約束點，3種搭接方法選擇的約束點相同，通過嚴密平差計算的CPⅢ方位角中誤差如表2和表3所示，主要精度指標如表4和表5所示。

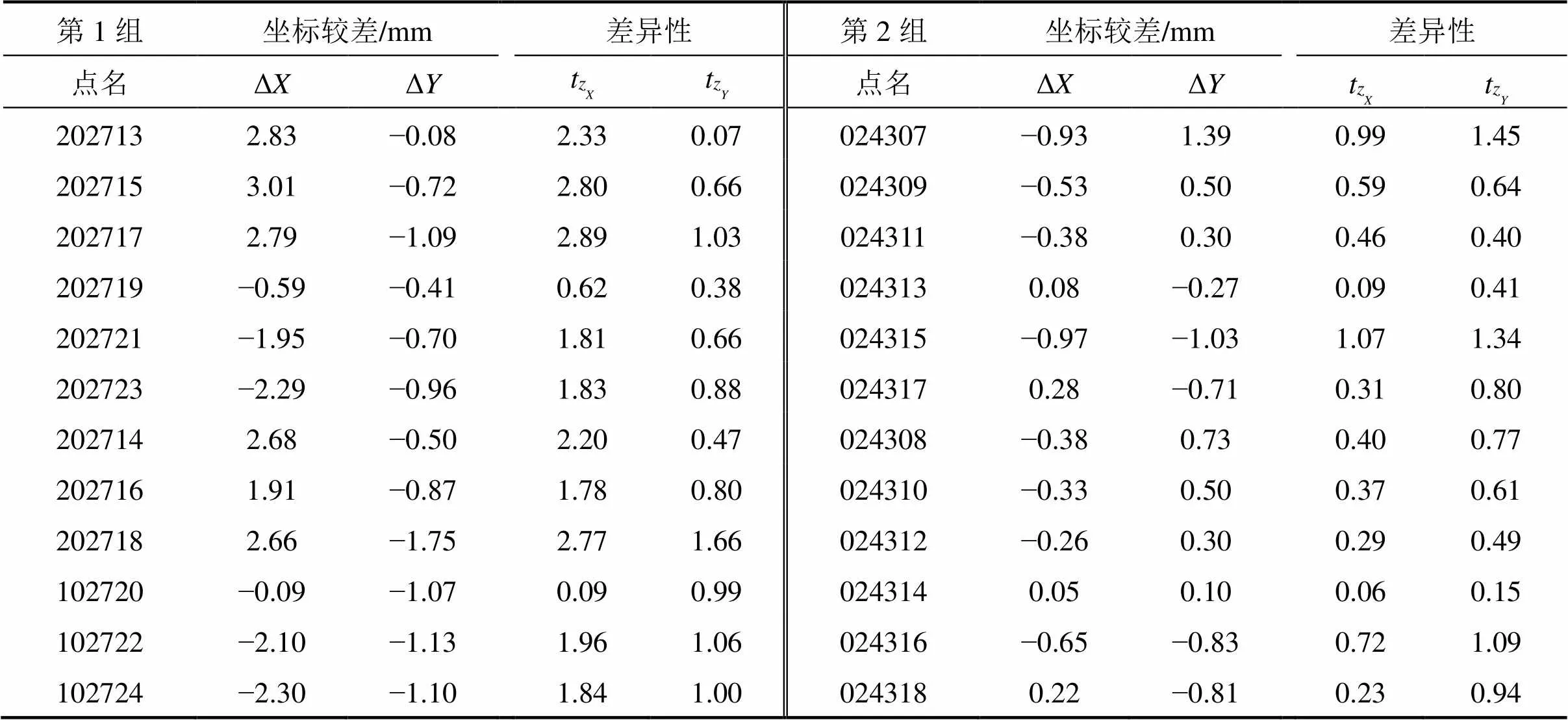
表1 相鄰區段獨立平差重疊點坐標較差及差異性

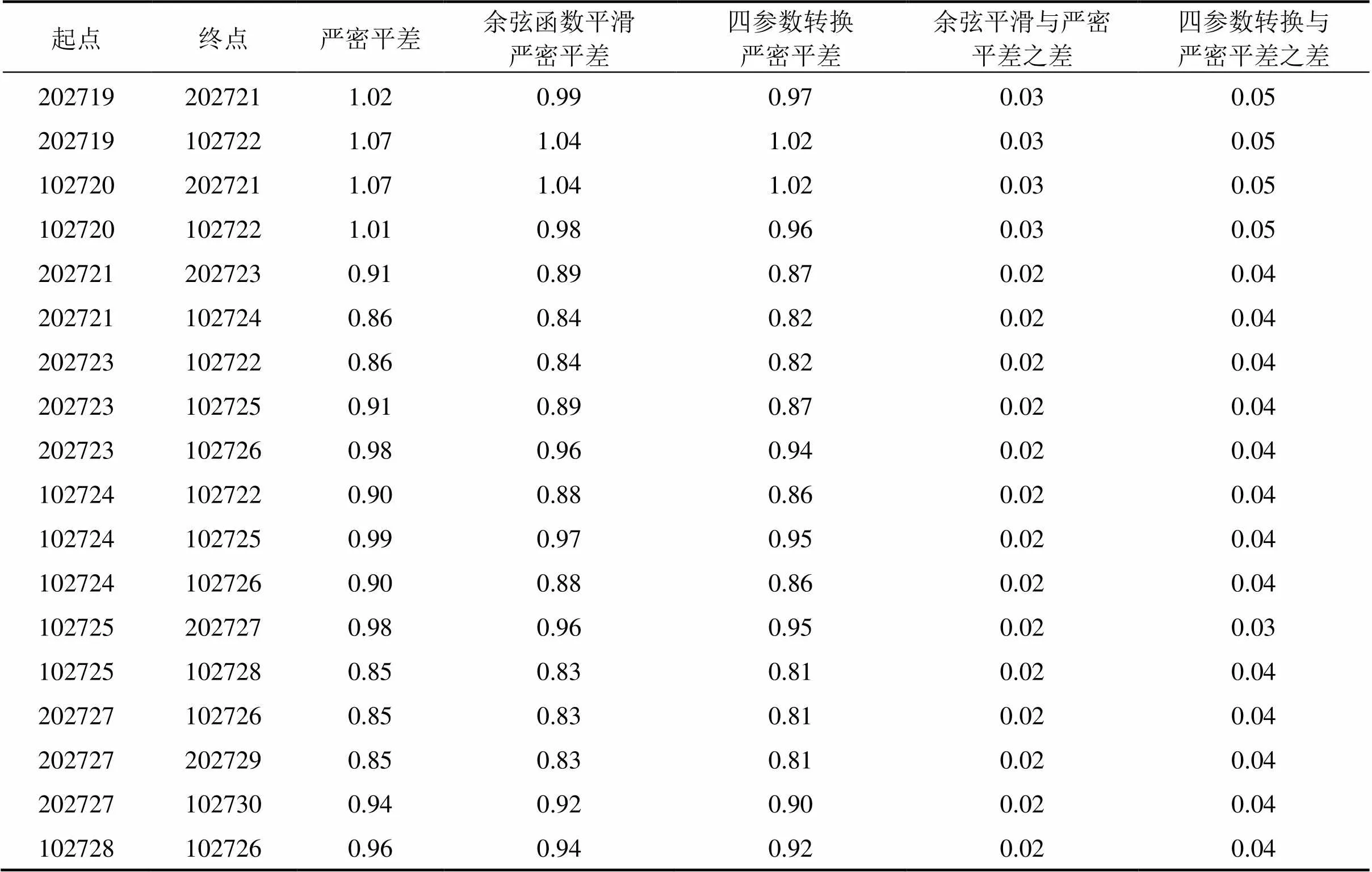
表2 3種搭接方法平差得到的方位角中誤差(第1組)

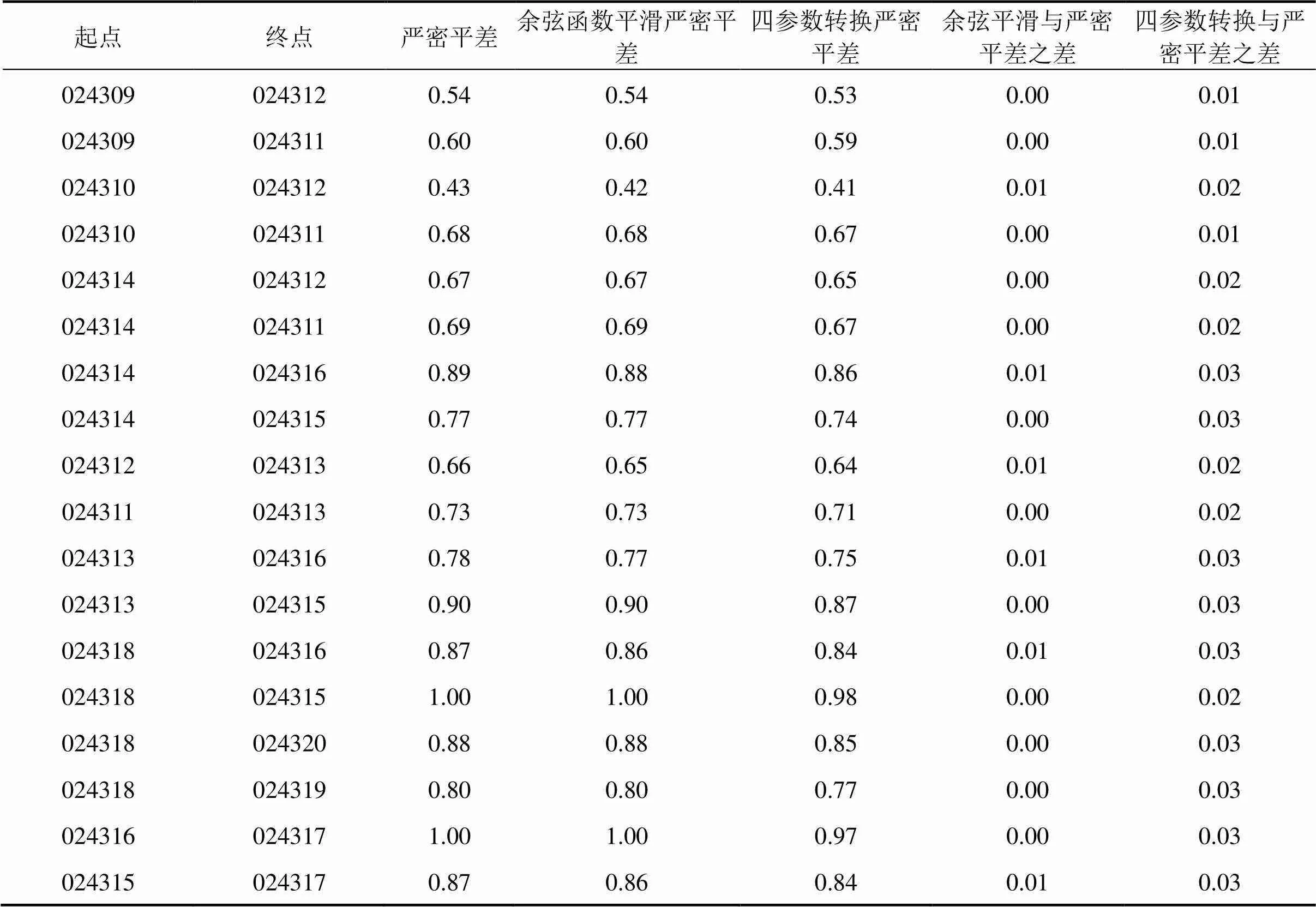
表3 3種搭接方法平差得到的方位角中誤差(第2組)

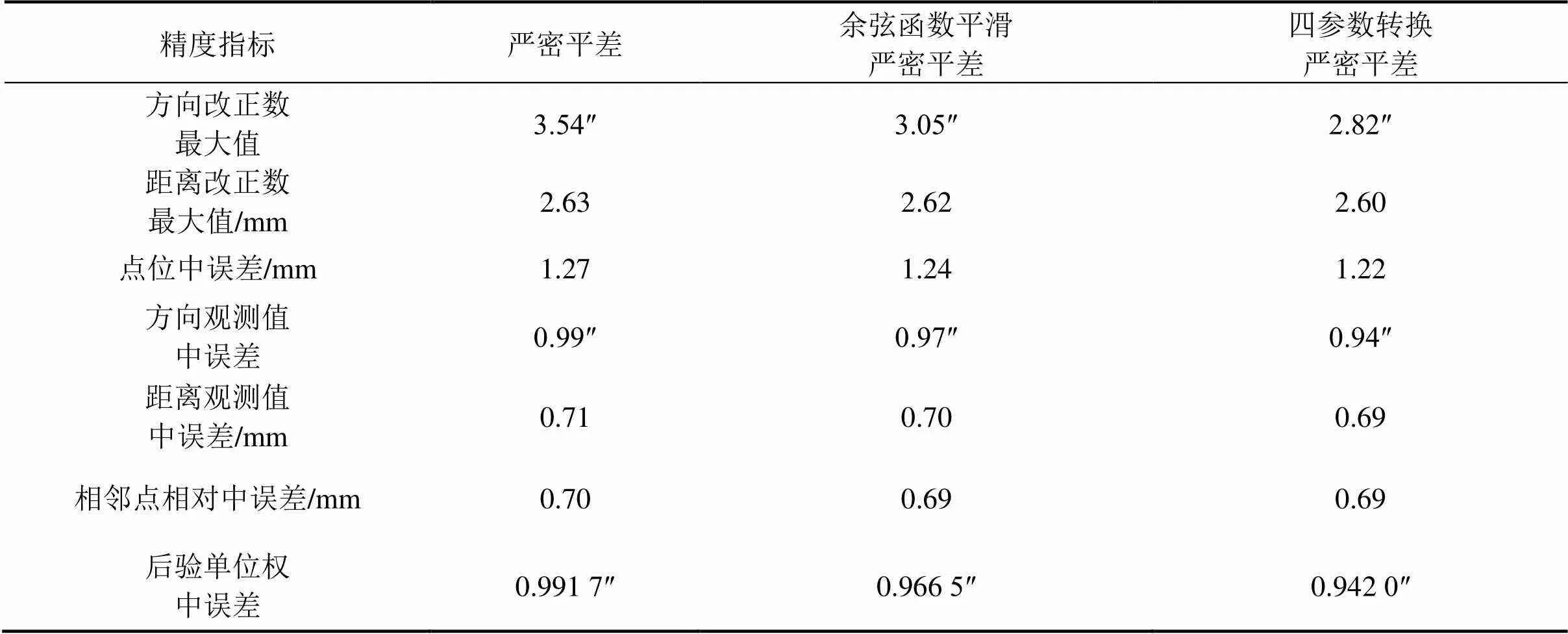
表4 3種搭接方法平差得到的CPⅢ網主要精度指標對比(第1組)

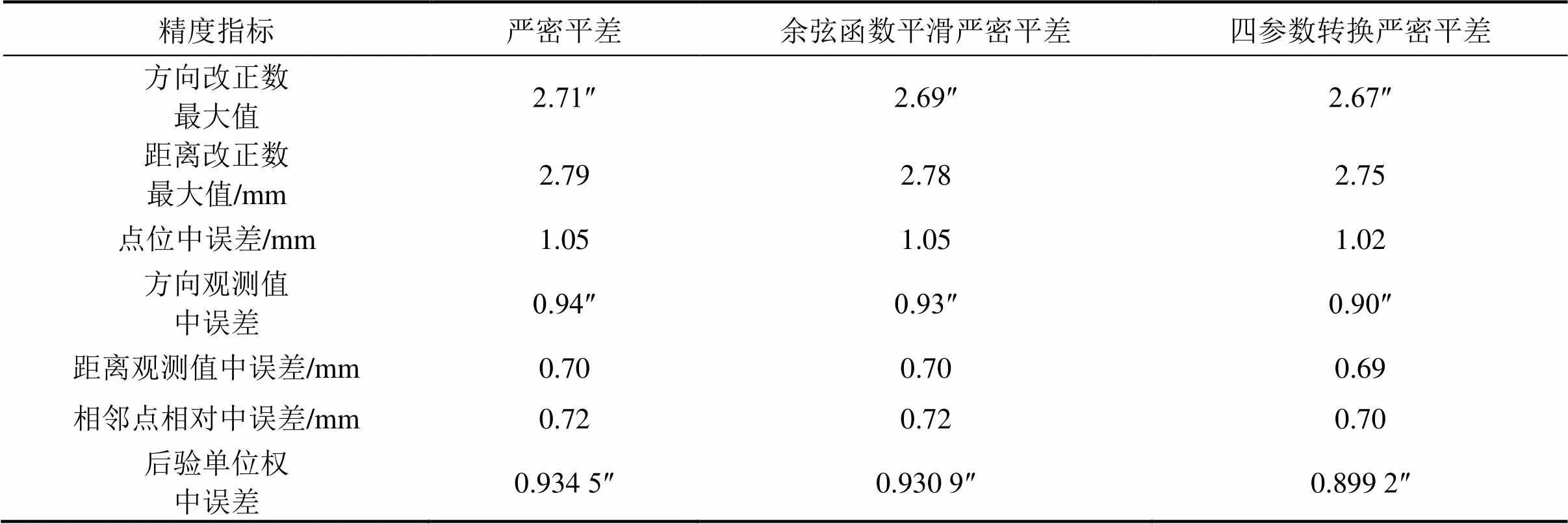
表5 3種搭接方法平差得到的CPⅢ網主要精度指標對比(第2組)

通過以上計算數據可以看出，3種方法在處理CPⅢ搭接區段時得到的各項精度指標，都滿足規范要求。從表2和表3可看出，嚴密平差的相對中誤差最大，四參數轉換嚴密平差的相對中誤差最小，余弦函數平滑嚴密平差的結果介于兩者之間。當搭接區段重疊點的坐標較差較大時，基于余弦函數平滑的嚴密平差法計算的搭接精度較嚴密平差法有一定程度的提高，但對于重疊點坐標較差較小時，基于余弦函數平滑的嚴密平差法精度提高不夠明顯；基于四參數轉換的嚴密平差法在處理兩組搭接數據時，方位角中誤差均有所改善。而表4和表5進一步驗證了四參數轉換嚴密平差法較嚴密平差法和余弦函數平滑嚴密平差法精度有所提高，其中方向改正數、距離改正數、點位中誤差、相鄰點相對中誤差、后驗單位權中誤差等精度指標都有改善，由此說明CPⅢ網的精度有一定程度提高，特別是重疊點較差較大時，精度改善比較明顯。

4 結論

1) 采用上述搭接方法處理CPⅢ平面數據之前，利用坐標差異性檢驗方法，選取點對的和方向坐標檢驗值均小于限差時，可以最大限度減弱人為選擇約束點的影響，科學合理選擇搭接區段的約束點。余弦函數平滑在處理搭接區段重疊點時，首先需要滿足相鄰區段重疊點獨立平差坐標較差不大于3 mm。若出現部分重疊點坐標較差大于3 mm，余弦函數平滑法會強行拉偏重疊點坐標，對搭接區段精度及后續軌道平順性維護都會產生不利影響。而四參數轉換法是將后區段重疊點坐標轉換至前區段坐標系統中，同時選取經差異性檢驗的所有重疊點作為轉換基準，利用改進的四參數轉換法削弱了轉換誤差，提高了轉換坐標的精度并改善了CPⅢ搭接區段的精度。

2) 通過對實測數據的對比計算與分析，發現：基于余弦函數平滑的嚴密平差法對于CPⅢ搭接區段精度提升不明顯。而采用基于四參數轉換的嚴密平差法處理搭接數據，對于重疊點坐標較差較大，甚至部分重疊點坐標較差超過3 mm的情況，搭接區段的方位角中誤差以及主要精度指標均有明顯改善；對于重疊點坐標較差較小的情況，搭接區段的各項精度指標也有一定程度的改善。這證明基于四參數轉換的嚴密平差法處理搭接數據更有效，能夠實現CPⅢ網平滑過渡，保證軌道的高平順性，滿足高速鐵路CPⅢ測量的實際需求。

[1] TB 10601—2009, 高速鐵路工程測量規范[S]. TB 10601—2009, Code for engineering survey of high speed railway[S].

[2] 黃志偉, 劉成龍, 王化光, 等. 高速鐵路CPⅢ平面控制網相鄰區段搭接方法研究[J]. 鐵道科學與工程學報, 2010, 7(6): 111?115. HUANG Zhiwei, LIU Chenglong, WANG Huaguang, et al. Research of lapping methods between adjacent regions for CPⅢ plane network in high-speed railway[J]. Journal of Railway Science and Engineering, 2010, 7(6): 111? 115.

[3] XIE Kaize, XING Jun, WANG Li, et al. Effect of temperature difference load of 32 m simply supported box beam bridge on track vertical irregularity[J]. Journal of Modern Transportation, 2015, 23(4): 262?271.

[4] 石德斌, 張彪, 王元昌, 等. 高速鐵路CPⅢ網區段搭接數據處理研究[J]. 鐵道工程學報, 2012, 29(2): 37? 40. SHI Debin, ZHANG Biao, WANG Yuanchang, et al. Research on sectional overlapping data processing of track control network for high-speed railway[J]. Journal of Railway Engineering Society, 2012, 29(2): 37?40.

[5] 周牧, 耿小龍, 謝良波, 等. 基于信號分布混合假設檢驗的Wi-Fi室內定位方法[J]. 電子與信息學報, 2018, 40(12): 2868?2873. ZHOU Mu, GENG Xiaolong, XIE Liangbo, et al. Wi-Fi indoor localization based on hybrid hypothesis test of signal distribution[J]. Journal of Electronics & Information Technology, 2018, 40(12): 2868?2873.

[6] Scagliarini M. A sequential hypothesis testing procedure for the process capability indexCpk[J]. Quality and Reliability Engineering International, 2018, 34(5): 791? 806.

[7] 謝建, 龍四春, 李黎, 等. 不等式約束加權整體最小二乘的凝聚函數法[J]. 武漢大學學報(信息科學版), 2018, 43(10): 1526?1530. XIE Jian, LONG Sichun, LI Li, et al. An aggregate function method for weighted total least squares with inequality constraints[J]. Geomatics and Information Science of Wuhan University, 2018, 43(10): 1526?1530.

[8] 陳洲, 高俊強. CPⅢ平面控制網前后區段搭接方法應用與研究[J]. 測繪與空間地理信息, 2019, 42(2): 172? 174. CHEN Zhou, GAO Junqiang. Research on lapping methods in front and rear sections for CPⅢ plane control network[J]. Geomatics & Spatial Information Technology, 2019, 42(2): 172?174.

[9] 彭思淳, 鄧興升. 坐標轉換四參數解算的整體最小二乘新方法[J]. 測繪工程, 2017, 26(9): 10?13, 22. PENG Sichun, DENG Xingsheng. A new method of total least squares algorithm for the plane four parameters coordinate transformation[J]. Engineering of Surveying and Mapping, 2017, 26(9): 10?13, 22.

[10] FANG Xing. A structured and constrained total l-eastsquares solution with cross-covariances[J]. Stu-dia Geophysica et Geodaetica, 2014, 58(1): 1?16.

[11] XU Peiliang, LIU Jingnan, SHI Chuang. Total least squares adjustment in partial errors-in-variables models: algorithm and statistical analysis[J]. Journal of Geodesy, 2012, 86(8): 661?675.

[12] 任曉春, 周東衛. 高速鐵路CPⅢ相鄰區段搭接方法研究與應用[J]. 鐵道工程學報, 2014, 31(6): 30?34, 45. REN Xiaochun, ZHOU Dongwei. Research and application on the lapping methods between adjacent sections for CPⅢ track control network for high-speed railway[J]. Journal of Railway Engineering Society, 2014, 31(6): 30?34, 45.

Research on lapping processing of high-speed rail CPⅢ adjacent section based on improved four-parameter rigorous adjustment method

JIANG Yinghao1, ZHANG Xianzhou1, 2, CHEN Xusheng1, XIA Chenxi1, CHEN Xiao1

(1. Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, Chengdu 610031, China;2. State-province Joint Engineering Laboratory of Spatial Information Technology for High-Speed Railway Safety, Chengdu 610031, China)

The track control network (CPIII) of high-speed railway mainly provides safe, stable and reliable control datum for track laying, fine adjustment and operating maintenance, and the lapping accuracy of CPIII adjacent sections directly affect track regularity. Based on the theory of hypothesis testing, the coordinate difference test method was used to process the independent adjustment coordinates of the overlapping points at adjacent sections, and the difference parameters of the overlapping points were obtained in order to select the overlapping points scientifically and reasonably. The shortcomings of the classical four parameter transformation method were analyzed, and the classical four parameter transformation method was optimized. On this basis, the advantages and disadvantages of traditional four parameter transformation method and cosine function smoothing method were analyzed and compared, and a rigorous adjustment lapping method based on four parameter transformation was proposed. Combined with specific engineering examples, this paper compared and analyzed three overlapping methods, which shows that the new lapping processing method can improve the lapping accuracy of CPIII effectively.

section lapping; difference test; improved four parameter transformation; rigorous adjustment lapping

P258

A

1672 ? 7029(2020)02 ? 0273 ? 07

10.19713/j.cnki.43?1423/u.T20190487

2019?06?01

上海鐵路局資助項目(LR01HX1135Y16035)

張獻州(1962?)，男，四川成都人，教授，從事大地測量、精密工程測量與變形觀測研究；E?mail：xzzhangswjtu@163.com

(編輯 蔣學東)