基準刑調節方法實證研究

●文 姬

量刑方法，包括量刑情節的區分和適用方法、基準刑的確定方法、基準刑調節方法。其中基準刑調節方法是量刑情節調節基準刑的方法。基準刑調節方法是量刑方法的重要組成部分。基準刑調節方法又包括兩個部分，即量刑情節調節基準刑的調節程式（簡稱“調節程式”）和量刑情節調節基準刑的調節幅度模式（簡稱“調節幅度模式”）。在我國，基準刑調節方法包括兩個方面的爭議：一是調節程式上有 “復合模式”和 “單一模式”的爭議；二是調節幅度模式上有“比例固定”模式和“數值固定”模式的爭議。要解決這兩方面的爭議，需要依據實證資料進行研究。本文將利用盜竊罪的實證數據，探討基準刑調節方法的上述兩個爭議。

一、基準刑調節方法的爭議

我國《關于常見犯罪的量刑指導意見》（簡稱《量刑指導意見》）對于明確量刑步驟，建立相對獨立的量刑程序，增強控辯雙方關于量刑的有效對抗，強調刑事政策和量刑原則對量刑的指導，細化和規范量刑情節的辨識和適用，構建科學、規范的量刑方法等，起到了重要的作用。〔1〕參見石經海：《中國量刑規范化之十年檢討與展望》，載《法律科學》2015年第4期；黃曉云：《量刑規范化改革在實踐中前行——訪最高人民法院刑三庭庭長戴長林》，載《中國審判新聞月刊》2011年第68期。但是，對于基準刑調節方法中，調節程式為什么采取復合模式，以及調節幅度模式為什么采用“比例固定”模式，《量刑指導意見》及相關司法解釋并沒有給出具體的理由，因而引起了刑法理論界和實務界的爭議。

（一）兩種調節程式的爭議

1.《量刑指導意見》中的調節程式：復合模式

我國《量刑指導意見》中的調節程式是復合模式。復合模式包含兩個方面：一是，對于一般量刑情節，采取“同向相加、逆向相減”的調節程式，用數學公式可表示為，基準刑×（1+從重情節的調節比例-從輕情節的調節比例）；二是，對于特定的量刑情節（如未成年人犯罪、限制行為能力的精神病人犯罪、又聾又啞的人或者盲人犯罪、防衛過當、避險過當、犯罪預備、犯罪未遂、犯罪中止、從犯、脅從犯和教唆犯等“修正量刑情節”），則采取“部分連乘、部分相加減”的調節程式，用數學公式可表示為，基準刑×（1-修正量刑情節1的調節比例）×……×（1-修正量刑情節n的調節比例）×（1+從重情節的調節比例-從輕情節的調節比例）。〔2〕參見南英主編、戴長林副主編、最高人民法院刑事審判第三庭編著：《量刑規范化實務手冊》，法律出版社2014年版，第32-35頁。筆者將復合模式定義為兩種調節程式相結合的量刑方法，而單一模式定義為只采取一種調節程式的量刑方法。這一定義與引文中的論述稍微有所區別。

與復合模式相對應的是單一模式。單一模式是指，不管對于一般量刑情節還是對于“修正量刑情節”，均采取“同向相加、逆向相減”的調節程式。

可見，復合模式和單一模式的區別在于，對于“修正量刑情節”，到底是采取“部分連乘、部分相加減”的調節程式，還是采取“同向相加、逆向相減”的調節程式。若是前者，則是復合模式；若是后者，則是單一模式。

例如，某案件中，被告人是未成年人減少基準刑50%的刑罰，且是從犯減少基準刑30%的刑罰，又具有累犯情節增加基準刑10%的刑罰，還具有自首情節減少基準刑20%的刑罰。如果采取復合模式進行計算，則被告人刑罰為：基準刑×（1-50%）×（1-30%）×（1+10%-20%）。如果采取單一模式進行計算，則被告人刑罰為：基準刑×（1-50%-30%+10%-20%）。

2.復合模式的優勢和弊端

對于復合模式，最高人民法院戴長林法官進行了如下說明：從理論上講，對“修正量刑情節”采用“同向相加、逆向相減”的單一模式得出的結果會出現零或者負數的情況。從適用情節合理性方面講，不同類型的量刑情節進行簡單加減，過于絕對化。從量刑思維過程來講，對未成年、未遂等“修正量刑情節”，應當先對基準刑進行調節，再用其他情節進行調節，這樣更符合刑法理論和量刑思維過程，得出的結果更具合理性。〔3〕參見戴長林、陳學勇：《量刑規范化改革與實踐》，載《法律適用》2011年第9期。然而，上述文字只是給出了復合模式優于單一模式的結論，這些結論并不完全正確或者明晰。首先，就第一點來說，復合模式和單一模式都會出現零或者負數的情況，這并不是復合模式的優勢；其次，就第三點來說，復合模式在哪些具體方面更具有合理性并不是很清晰。所以，需要更深入地比較兩種調節程式的優劣。

徐嘎學者贊成復合模式，認為復合模式符合“罪行輕重不同的被告人如果具有相同的量刑情節，從輕的幅度相同但從輕的刑期可以不同”的量刑規律。例如，（案例1）甲盜竊他人活期存折一個，存折上存有30 萬元，因甲取款時神色慌張，被銀行人員發現而未能取走現金，屬犯罪未遂，事后主動投案自首。（案例2）乙盜竊他人現金30 萬元既遂，犯罪后主動投案自首。如果盜竊30 萬元的基準刑為有期徒刑10 年，自首從輕20%，未遂從輕30%，那么按照復合模式，先考慮犯罪未遂情節，然后考慮自首情節，則案例1中甲盜竊30萬元未遂中，自首從輕刑期是10×（1-30%）×20%，即1.4年；而案例2中甲盜竊30 萬元既遂中，自首從輕刑期是10×20%，即2 年。兩者從輕的幅度相同，但是從輕的刑期不同。案例1的未遂犯罪中，自首從輕的刑期要少些。這充分體現了“罪行輕重不同的被告人如果具有相同的量刑情節，從輕的幅度相同但從輕的刑期可以不同”的量刑規律。〔4〕參見徐嘎：《犯罪行為與犯罪人：量刑根據的二元化——兼論量刑規范化改革關于量刑步驟的合理構建》，載《山東審判》2010年第3期。案例根據本文需要，在細節上有所更改，但基本原理與原文一致。

耿磊學者則不贊成復合模式，認為單純從數學角度出發，復合模式也存在以下問題。第一，“部分連乘、部分相加減”的調節程式將修正量刑情節與一般量刑情節相互關聯、相互作用、相互影響，并且隔斷了一般量刑情節對基準刑的直接作用。第二，認為運用復合模式的調節程式仍無法回避最終宣告刑為零和負數的尷尬。第三，立法原意本為強調修正量刑情節的影響，但是這種調節程式反而會降低修正量刑情節的影響。例如，（案例3）丙是未遂減少30%的刑罰，且具有自首也減少20%的刑罰。（案例4）丁是既遂，具有自首情節減少20%的刑罰，以及獲得被害人諒解情節減少30%的刑罰。按照強調“修正量刑情節”的立法原意，整體上看，案例3采取復合模式減少的刑期應該比案例4采取單一模式減少的刑期要多些；單個情節上看，未遂減輕的刑期應該比被害人諒解減輕的刑期要多些。然而，事實并非如此。在基準刑10年的情況下，整體上看，案例3中丙的量刑為：10×（1-30%）×（1-20%），為5.6年，減少4.4年；案例4中丁的量刑為：10×（1-20%-30%），為5年，減少5年。案例3減少的刑期比案例4減少的刑期要少些，這與立法原意相違背。并且，從單個情節上看，案例3中未遂減少2.4年，自首減少2年；〔5〕就案例3而言，按照《量刑指導意見》，應該是未遂減少3年，自首減少1.4年，與案例1相同。所以，這里耿磊學者的分析有誤，但其最終結論卻是正確的。案例4中被害人諒解減少3年，自首減少2年。未遂減輕的刑期少于被害人諒解減輕的刑期，也與立法原意相違背。〔6〕參見耿磊：《酌定量刑情節規范化路徑》，法律出版社2017年版，第132-135頁。案例根據本文需要，在細節上有所更改，但基本原理與原文一致。

上述兩位學者列舉類似的案例，卻得出截然不同的結論。就一般量刑情節的量刑效果而言，徐嘎學者的觀點是正確的。在相同的基準刑和調節幅度下，相比于單一模式，復合模式減輕的刑期要少些。根本原因在于，復合模式中，修正量刑情節的連乘法使得基準刑處于不停減少的狀況。基準刑的減少使得調節幅度相同的一般量刑情節，實際減少或者增加的刑期也要少些。

然而，耿磊學者的最終結論也是正確的。復合模式中的連乘法，并沒有如立法原意所示，強化“修正量刑情節”的減輕幅度，反而弱化了“修正量刑情節”的減輕幅度。首先，案例3中未遂情節減輕的30%，等于案例4中被害人諒解情節減輕30%，均為3年。“修正量刑情節”未遂情節減輕的刑期并不比“一般量刑情節”被害人諒解減輕的刑期多，沒有如立法原意強化“修正量刑情節”的減輕幅度。其次，如果同時存在兩個及以上的“修正量刑情節”的情況下，可以認為第二個以后的“修正量刑情節”減輕的刑期要比“一般量刑情節”減輕的刑期少。例如，（案例5）戊是未成年減少50%的刑罰，同時是未遂減少30%的刑罰，還具有自首也減少20%的刑罰。在基準刑為10年的情況下，案例5中未遂減少的30%是以5年為基準刑，減少1.5年的刑期。而案例4中，被害人諒解減輕的30%是以10年為基準刑，減少的是3年的刑期，遠遠多于案例5“修正量刑情節”未遂減輕的刑期。最后，不僅就單個情節而言，“修正量刑情節”未遂減輕的刑期不多于“一般量刑情節”被害人諒解減輕的刑期。并且，整體而言，有“修正量刑情節”的案例中減輕的刑期要小于沒有“修正量刑情節”的案例。例如，有“修正量刑情節”的案例3中，減輕的刑期為4.4年，小于沒有“修正量刑情節”的案例4中減輕的刑期5年。這也說明復合模式的連乘法，沒有強化“修正量刑情節”的減輕幅度。

由此可見，復合模式較單一模式更為復雜，但在理論上并不具有明顯的優勢，相反，其弊端很明顯。首先，復合模式的基準刑處于不停的變動中，使得基準刑失去了作為“基準”的意義。其次，復合模式中的連乘法，并沒有如立法原意所示，強化“修正量刑情節”的減輕幅度。

所以，要支持復合模式，必須從司法實務角度出發。如果復合模式得到的宣告刑值，比單一模式得到的宣告刑值，更接近司法實踐中的實際宣告刑值，那么盡管復合模式理論上有諸多不足，也值得提倡。反之，如果復合模式得到的宣告刑值，并不比單一模式得到的宣告刑值，更接近司法實踐中的實際宣告刑值，則復合模式不值得提倡。本文將利用盜竊罪案例的數據，通過實證研究方法，來考察復合模式的預測宣告刑，是否要比單一模式的預測宣告刑更接近司法的實際宣告刑。

值得說明的是，我國司法實踐中的量刑方法來源于復合模式，是否司法實踐得到的宣告刑就一定會更符合復合模式呢？其實不然。首先，我國幅員遼闊，各地即使是嚴格按照復合模式去執行，仍然在選擇量刑起點、調節比例時存在自由裁量權，這種自由裁量權導致各地的執行結果并不一定一致地符合同一個復合模式。例如，甲地盜竊罪量刑起點為2 000元，未遂的調節比例為30%，自首的調節比例為30%；而乙地盜竊罪量刑起點選擇3 000元，未遂的調節比例為50%，自首的調節比例為20%。假設，行為人A盜竊6 000元財物，那么，甲地對A在量刑起點4個月的基礎上，增加4個月，構成基準刑8個月，然后因為未遂減少30%，得到5.6個月，最后因為自首減少30%，得到宣告刑3.92個月。不同的是，乙地對A在量刑起點6個月基礎上，增加3個月，構成基準刑9個月，然后因為未遂減少50%，得到4.5個月，最后因為自首減少20%，得到宣告刑3.6個月。對甲地和乙地兩種不同情況進行一般線性回歸的結果，可能是復合模式：8×（1-40%）×（1-20%），擬合的宣告刑為3.84個月，也可能是單一模式：8×（1-38%-15%），擬合的宣告刑為3.76個月。復合模式中，預測值和實際宣告刑的殘差平方和為0.064；單一模式中，預測值和實際宣告刑的殘差平方和為0.051；前者大于后者，所以單一模式要優于復合模式。〔7〕從統計學角度看，殘差平方和小的擬合方程更具有優勢。可見，對于具有裁量差異的來源于復合模式的實證數據，最后擬合的復合模式和單一模式之間的結果相差無幾，并不一定得到復合模式優先于單一模式的結論。其次，復合模式和單一模式雖然形式上相差甚大，但是最后的實際量刑數值相差并不一定很大。例如，在基準刑是10年的基礎上，未遂減少50%，自首減少20%的情況下，復合模式為：120×（1-50%）×（1-20%），宣告刑為48個月；而單一模式為：120×（1-50%-20%），宣告刑為36個月。兩者相差12個月，即1年。這是相差較大的情況。基準刑越低的時候，兩種模式的宣告刑相差越小。而司法實踐中，絕大多數案件基準刑都小于5年，所以宣告刑也會相差較小。總之，司法實踐中數據雖然來源于復合模式，但是眾多案例匯總后線性回歸擬合的結果并非一定是復合模式優先于單一模式。

如果眾多案例匯總后得到的結果是單一模式優先于復合模式，那么即使實際數據來源于復合模式，我們仍應該將之統一為單一模式，從而實現基準刑調節程式的簡化改革。這樣簡化改革的結果當然會造成各地裁量權的減弱，但是會使各地量刑更加具體化和統一化。

（二）兩種調節幅度模式的爭議

1.《量刑指導意見》中的調節幅度模式：比例固定

我國《量刑指導意見》中的調節幅度模式是“比例固定”模式。所謂的“比例固定”模式是指，常見量刑情節對基準刑的調節比例雖然存在一定的浮動幅度，但是這一浮動幅度是針對情節本身的嚴重程度而言的，并不是針對不同罪名而言；對于不同的罪名，同一常見量刑情節的調節比例相對固定。例如，《量刑指導意見》第3條第1項規定，已滿16周歲不滿18周歲的未成年人犯罪，減少基準刑的10%～50%。那么，針對不同的罪名，未成年犯罪均減少基準刑的刑罰幅度范圍一致，均為10%～50%。只是在不同案件中，具體減少的調節比例，根據犯罪行為的動機和目的、犯罪時的年齡和對犯罪的認識能力、悔罪表現、個人成長經歷和一貫表現等來決定。〔8〕同前注〔2〕，南英主編書，第52頁。

例如，（案例6）被告人己17歲11個月，輟學，經常小偷小摸，一次詐騙30萬元，基準刑為8年。（案例7）被告人庚16歲5個月，學校表現良好，偶爾的一次盜竊30萬元，基準刑為10年。在盜竊罪和詐騙罪兩種不同的犯罪中，未成年情節調節基準刑的“比例固定”均為10%～50%。但是案例6中，被告人是一貫表現不好，且年齡稍長；而案例7中被告人一貫表現好，且年齡稍小。所以，案例6中未成年減輕比例可以設定為20%，而案例7中未成年減輕比例可以設定為40%。

2.“集體經驗法”中的調節幅度模式：數值固定

對于調節幅度模式，除了《量刑指導意見》中的“比例固定”模式外，還有白建軍教授主張的“集體經驗說”中的“數值固定”模式。

“集體經驗說”是一種根據法官集體經驗，利用統計學方法構建起來的量刑模式。〔9〕該量刑方法即統計學中的回歸方法，參見白建軍：《基于法官集體經驗的量刑預測研究》，載《法學研究》2016年第6期。“集體經驗說”具有以下幾個特點：第一，“集體經驗說”計算刑罰的公式是一個線性回歸方程。用數學公式表達為：刑罰量=b0+b1×基準事實情節1+b2×基準事實情節2+b3×一般量刑情節1+b4×一般量刑情節2+……+bn×一般量刑情節n。第二，量刑起點為“裸刑均值”，處于法定刑的偏低幅度。“裸刑均值”是指一組沒有其他量刑情節，只有犯罪構成事實的生效判決的刑罰均值。〔10〕參見白建軍：《裸刑均值的意義》，載《法學研究》2010年第6期。第三，基準事實是對刑罰量影響最大的幾個量刑情節。例如，在醉酒型危險駕駛罪中，對刑罰量影響最大的量刑情節是血液酒精含量、車型等，所以其基準刑可通過血液酒精含量、車型來構建。〔11〕參見文姬：《醉酒型危險駕駛罪量刑影響因素實證研究》，載《法學研究》2016年第1期。第四，基準刑是在量刑起點的基礎上通過加法的方式獲得。以刑罰量（或者刑罰的對數變形〔12〕例如，有時候為了滿足線性回歸的方差齊性的要求，將因變量或者自變量進行Lg或者Ln的對數變形。）為自變量，以量刑情節（或者量刑情節數值的對數變形）為因變量的回歸，一般來說是線性回歸。所以，基準刑與基準事實取值之間要么是呈線性增長，要么是呈指數增長或者對數增長。指數增長和對數增長也可以轉化為分段的線性增長。例如，就醉酒型危險駕駛罪來說，對所有的樣本案件進行線性回歸，得到回歸直線，從而得到基準刑的程式：拘役天數=28.581+0.241×血液酒精含量。〔13〕同前注〔11〕，文姬文。所以，其量刑起點為：拘役天數=28.581+0.241×80，約為48天。刑罰增量為：血液酒精含量每增加6mg/100mL，刑期增加1個月。第五，調節程式為“同向相加，逆向相減”的單一模式。因為“集體經驗法”是運用的線性回歸方法，量刑情節之間是以加減法相連接的。第六，調節幅度模式為“數值固定”模式，即常見量刑情節對基準刑的調節幅度模式是通過加減固定的數值，而非加減固定的比例。

“集體經驗說”中，調節幅度模式為“數值固定”模式。例如，自首在盜竊數額為5萬元～40萬元的盜竊罪中，回歸系數為12.544。其代表的意義是，具有自首情節的案件比具有配合情節的案件，行為人的刑期要少約13個月。〔14〕數據見本文第二部分表1中盜竊數額為5萬元～40萬元時的“數值固定”模式。也就是說，在盜竊罪中，自首情節是在基準刑的基礎上增加“固定數值”的刑期，即13個月。

比較而言，《量刑指導意見》中的調節幅度模式為“比例固定”模式。例如，《量刑指導意見》規定自首減少基準刑的40%以下的刑罰量。假設減少40%，那么用數學公式表示自首減輕的刑期為：40%×基準刑=40%×（量刑起點+刑罰增量）。按照江蘇省的規定來算，5萬元～40萬元的盜竊罪中，盜竊5萬元對應的量刑起點為42個月，每增加5 000元增加1個月的基準刑。自首則減少的刑期為：40%×（量刑起點+刑罰增量）=40%×（42+盜竊數額增量），約17個月到45個月不等。可見，同一個罪名中，因為基準刑隨著盜竊數額的增加而不同，自首減少的天數也不同。不同的罪名中，由于量刑起點和刑罰增量的不同，自首減少的天數也不相同。自首減少的天數，與量刑起點數成正比，與刑罰增量成正比。所以，在《量刑指導意見》中，自首對基準刑的調節幅度不是“數值固定”，而是“比例固定”。

3.“比例固定”模式與“數值固定”模式的區別

《量刑指導意見》中的“比例固定”模式和“集體經驗說”中的“數值固定”模式均來源于法官的集體經驗，這使得它們在本質上具有相同性。〔15〕《量刑指導意見》中常見情節的調節比例的確定方法，并不能從公開的資料獲得。《量刑指導意見》的開頭指出：“根據刑法和刑事司法解釋等有關規定，結合審判實踐，制定本指導意見。”可見，《量刑指導意見》中常見情節的調節比例的確定，肯定參考了審判中的大量案例。所以，稱其為“來源于法官的集體經驗”。但是，“比例固定”模式和“數值固定”模式還是存在以下兩點顯著差別。

首先，“比例固定”模式較“數值固定”模式更為復雜。其一，“數值固定”模式中，量刑情節對基準刑的調節數值是固定不變的。而在“比例固定”模式中，調節數值實際上與量刑起點和刑罰增量均成正比。在同一罪名的不同量刑幅度或者不同罪名中，量刑起點和刑罰增量處于不斷變動中，從而“比例固定”模式中的調節數值也隨著兩者的變動而處于不斷的變動中。其二，如果將“比例固定”模式的公式拆分成由加減法構成的線性模式，〔16〕參見本文第二部分：調節幅度模式的實證研究中的關于兩種調節幅度模式的“理論模型”。會發現在沒有“修正情節”的情況下，“比例固定”模式比“數值固定”模式多了“盜竊數額”與所有量刑情節的交互項，也就是說，“比例固定”模式考慮了交互影響，而“數值固定”模式沒有考慮交互影響。

其次，“比例固定”模式中，同一常見量刑情節在不同罪名中的調節比例是“固定”的；而在“數值固定”模式中，同一常見量刑情節在不同罪名中的調節數值是不固定的。《量刑指導意見》中給出未成年、未遂、從犯、自首、坦白、立功等情節的調節幅度，分別為10%～60%、0%～50%、20%～100%、0%～100%、0%～50%、0%～100%，并且，影響具體調節幅度的因素包括具體年齡、犯罪的嚴重程度、情節的社會效果等，但是，罪名并沒有成為具體調節幅度的影響因素。

罪名是否對同一情節的調節幅度具有顯著影響，這一問題的論證是個復雜的系統工程，筆者將另行贅述。對于量刑情節對基準刑的調節數值，是否應當與“基準刑”成正比，是否應當考慮“盜竊數額”與其他情節的交互效應，這兩個問題都是純數據方面的問題，理論上沒有優劣可言。所以，本文通過實證研究對兩者進行比較。并且，“比例固定”模式和“數值固定”模式兩者本質上均是“法官集體經驗”的產物，其構建的主要依據都是“一定數量的判決書”，所以應當從經驗上去論證兩者的優劣：與實踐擬合度更高的調節幅度模式更具有優勢。如果兩種調節幅度模式沒有顯著差異，則應當選擇更為簡單易行的“數值固定”模式。

二、調節幅度模式的實證研究

根據公安部門的統計資料，2013年到2015年間，盜竊罪立案數占到公安部門總立案數的67%～68%。〔17〕數據來源于《中國法律年鑒》2014、2015、2016年版本中的第1141、1022、1305頁。本文盜竊罪判決書的判決日期為2013—2015年。所以本文以盜竊罪為例，根據盜竊罪的實證數據，比較在調節程式為“同向相加、逆向相減”的情況下，“比例固定”和“數值固定”兩種不同調節幅度模式的優劣。

兩種不同調節幅度模式的優劣比較步驟如下：首先，利用司法實踐數據估算出“比例固定”模式和“數值固定”模式的理論模型的系數；其次，根據兩種理論模型，計算出各自的預測宣告刑；再次，計算兩個預測宣告刑與實際宣告刑之間的差的平方和，也就是殘差平方和；最后，檢驗兩種殘差平方是否具有顯著性差異。殘差平方和顯著偏小的調節幅度模式更具有優勢。

本文的數據來源于“中國裁判文書網”，收集日期為 2016年7月26日。在136 570個盜竊罪中，按照分層隨機方法，抽取了 1 806份判決書，〔18〕首先，按照各省人口比例對2 000份判決書進行分配，然后，對各省的判決書按照隨機等距抽樣方法進行隨機抽樣。刪除其中一些數據不完整、重復的案例，剩下1 806份案例。形成 2 355個記錄。〔19〕因為存在共同犯罪，所以記錄數多于判決書數目。

（一）案例選擇

合適的案例是計算出理論模型系數的基礎。

首先，案例中必須排除連乘法的適用。在“同向相加、逆向相減”的調節程式中，不能出現連乘法。所以本文選擇沒有“未成年犯罪、老年犯罪、限制行為能力的精神病人犯罪、又聾又啞的人或者盲人犯罪、防衛過當、避險過當、犯罪預備、犯罪未遂、犯罪中止、從犯、脅從犯、教唆犯”等“修正量刑情節”的案例記錄共2 113個。

其次，為了比較研究更容易實行，本文只考慮以“盜竊數額”為基準事實的情況。所以，理想狀況下，本文還要選擇沒有“扒竊、多次盜竊、入戶盜竊、攜帶兇器盜竊”情節的案例，從而排除以盜竊次數、盜竊手段為基準事實的情況出現。但是，在刪除所有的“扒竊、多次盜竊、入戶盜竊、攜帶兇器盜竊”案例的情況下，5萬元～40萬元的記錄只有66個，40萬元及以上的記錄只有16個，導致樣本量不夠。所以，本文僅僅在0～5萬元階段刪除所有有“扒竊、多次盜竊、入戶盜竊、攜帶兇器盜竊”情節的案例，而在5萬元～40萬以及40萬元以上的情況下，不刪除有“扒竊、多次盜竊、入戶盜竊、攜帶兇器盜竊”情節的案例。另外，因為單處罰金和管制并沒有統一折算的方法，加之記錄數量較少，所以予以刪除。還有，根據散點圖，盜竊數額0～5萬元的記錄中有1個異常值，最終得到盜竊數額為0～5萬元的記錄770個，5萬元～40萬元的記錄198個，40萬元及以上的記錄40個，共1 008個記錄。

（二）兩種調節幅度模式的理論模型

在1 008個盜竊罪記錄中，除盜竊數額外，量刑情節包括初犯、被害人諒解、積極繳納罰金和財產保證、立功、退贓退賠、認罪態度（包括自首、坦白、配合）、前科、累犯、其他從輕情節、其他從重情節、攜帶工具等。

1.“比例固定”模式的理論模型

在“同向相加、逆向相減”的調節程式下，“比例固定”模式的盜竊罪的刑罰量計算公式為：盜竊罪拘役刑或徒刑刑期=（b0+b1×盜竊數額）×（1+a1×初犯+a2×被害人諒解+a3×積極繳納罰金和財產保證+a4×立功+……+a12×攜帶工具+a13×扒竊+a14×多次盜竊+a15×入戶盜竊+a16×攜帶兇器盜竊）=b0+b1×盜竊數額+c1×初犯+c2×被害人諒解+c3×積極繳納罰金和財產保證+c4×立功+……+c12×攜帶工具+c13×扒竊+c14×多次盜竊+c15×入戶盜竊+c16×攜帶兇器盜竊+d1×初犯×盜竊數額+d2×被害人諒解×盜竊數額+d3×積極繳納罰金和財產保證×盜竊數額+d4×立功×盜竊數額+……+d12×攜帶工具×盜竊數額+d13×扒竊×盜竊數額+d14×多次盜竊×盜竊數額+d15×入戶盜竊×盜竊數額+d16×攜帶兇器盜竊×盜竊數額。其中，（b0+b1×盜竊數額起點）是量刑起點，（b1×盜竊數額增量）為基準刑的刑罰增量，（b0+b1×盜竊數額）是基準刑。（c1+d1×盜竊數額）/（b0+b1×盜竊數額）是初犯情節的調節比例……（c16+d16×盜竊數額）/（b0+b1×盜竊數額）是攜帶兇器盜竊情節的調節比例。〔20〕公式中比量刑情節數多一項，是因為認罪情節在公式中拆分為了兩項：自首、坦白。配合是參照情節，不體現在公式中。

之所以將理論模型拆解為一般線性方程，是因為我們在求解最優回歸方程時，是用“一般線性回歸”方法求得。所以，將理論模型拆解為一般線性方程，以便進行對比研究。

2.“數值固定”模式的理論模型

“數值固定”模式，也即“集體經驗法”中的調節幅度模式。其刑罰的計算公式為：盜竊罪拘役刑或徒刑刑期=B0+B1×盜竊數額+C1×初犯+C2×被害人諒解+C3×積極繳納罰金和財產保證+C4×立功+……+C16×攜帶兇器盜竊。其中，（B0+B1×盜竊數額起點）是量刑起點，（B1×盜竊數額增量）為基準刑的刑罰增量，（B0+B1×盜竊數額）是基準刑。C1是初犯情節的調節數值……C16是攜帶兇器盜竊情節的調節數值。

3.理論模型系數的計算

理想狀況下，上述兩種理論模型的系數均能夠運用盜竊罪的司法數據通過“一般線性回歸”方法求得。并且，在“比例固定”模式的理論模型中，各種量刑情節的比例能夠被計算出來，即（c1+d1×盜竊數額）/（b0+b1×盜竊數額）……（c16+d16×盜竊數額）/（b0+b1×盜竊數額）能夠除盡，沒有余數。

然而，理想情況幾乎不可能出現。一般會出現以下兩種不理想的狀況：第一，某些量刑情節不能夠被納入方程。例如，利用本文數據，在兩種理論模型的擬合中，初犯情節的交互效應項〔21〕交互效應項，是指線性方程中有兩個及以上量刑情節共同構成的項。如d1×初犯×盜竊數額、d2×被害人諒解×盜竊數額、d3×積極繳納罰金和財產保證×盜竊數額、d4×立功×盜竊數額、……、d16×攜帶兇器盜竊×盜竊數額。和主效應項〔22〕主效應項，是指線性方程中只有一個量刑情節構成的項。如c1×初犯、c2×被害人諒解、c3×積極繳納罰金和財產保證、c4×立功、……、c16×攜帶兇器盜竊等。的系數均大于零。這說明無論如何，初犯情節對刑罰的影響均為正向關系，即初犯情節導致刑罰量增加，這顯然與初犯情節是從輕情節的理論相矛盾。所以，初犯情節不能被納入方程中。第二，“比例固定”模式的模型中，各個量刑情節的比例不能夠被除盡，即（c1+d1×盜竊數額）/（b0+b1×盜竊數額）……（c12+d12×盜竊數額）/（b0+b1×盜竊數額）中全部或者部分不能夠被除盡，這說明純粹的“比例固定”模式的理論模型在某種程度上不能夠被獲得。

基于以上兩種不理想的狀況，本文采取變通的方法計算理論模型的系數，分別求出具有交互效應項的最優回歸方程和不具有交互效應項的最優回歸方程，用前者來擬合“比例固定”模式的理論模型，用后者來擬合“數值固定”模式的理論模型。因為從上面兩種理論模型的一般線性展開項可以發現，“比例固定”模式與“數值固定”模式的理論模型的主要區別在于，“比例固定”模式中具有交互效應項，而“數值固定”模式中不具有交互效應項，所以用具有交互效應項的最優回歸方程擬合“比例固定”模式的理論模型，而用沒有交互效應項的最優回歸方程擬合“數值固定”模式的理論模型。

（三）最優調節幅度模式的獲取方法

計算出理論模型的系數后，還需要比較兩個最優回歸方程中，哪個方程更具有實踐優勢。這需要用“均值比較”方法進行檢驗。

首先，利用“一般線性回歸”方法得到“比例固定”和“數值固定”兩種模式各自的最優回歸方程的同時，也可以計算出兩者的預測宣告刑。其次，計算預測宣告刑與實際宣告刑的差的平方和，即殘差平方和。殘差平方和小的調節幅度模式效果更佳。這是典型的“最小二乘法”思想。〔23〕參見理查德·P.魯尼恩、凱·A.科爾曼、戴維·J.皮滕杰：《行為統計學基礎》（第9版），王星譯，中國人民大學出版社2007年版，第183頁。最后，還需要用“成對樣本均值檢驗法”檢驗兩個殘差平方是否具有顯著性差異。因為即使兩種調節幅度模式的預測宣告刑與實際宣告刑具有一定的差異（其實具有差異是肯定的），還需要知道這種差異是否具有顯著性。如果具有顯著性，則說明兩種模式中，殘差平方和小的調節幅度模式確實具有顯著優勢；如果不具有顯著性，則說明殘差平方和小的調節幅度模式并不具有顯著優勢。具有顯著優勢的調節幅度模式，才是我們要提倡的最優調節幅度模式。所以，還需要檢驗兩個預測宣告刑與實際宣告刑的差的平方之間均值是否具有顯著性差異。這種檢驗方法稱為“成對樣本均值檢驗法”。

（四）一般線性回歸方程的結果分析

上述回歸系數和預測宣告值的求得方法為統計軟件SPSS中的一般線性回歸方法。因為本文的最終目的是比較預測宣告刑和實際宣告刑之間的差的平方和，而非考察影響量刑的顯著性因素，所以本文在進行一般線性回歸時，將所有的量刑情節都納入方程，而不考慮量刑情節的影響是否顯著。

1.“比例固定”模式和“數值固定”模式的最優回歸方程的獲取

（1）“比例固定”模式的理想的理論模型不能夠被獲取

按照“比例固定”模式的理想的理論模型，應當將所有的量刑情節及其交互效應項均納入方程。然而，本文的數據卻顯示，在盜竊數額為0～5萬元回歸方程中，并非所有的交互項均能夠被納入方程。

利用一般線性回歸方法，在將所有的交互效應項均納入模型后，得到自首的從輕的數值為-（0.000374×盜竊數額-0.452）。這一數值是基準刑（0.000768×盜竊數額+3.259）的-0.486倍又另外加上2.036個月（我們用-48.6%（+2.036）表示自首的調節比例）。〔24〕此處即為回歸方程中，量刑情節調節基準刑的調節比例的計算方法。下面所有量刑情節的調節比例均用這種方式表示：百分數部分是調節比例，括號內的常數部分是另外加上的調節數值。并且，用同樣的方法可以算得：初犯的調節比例為+59%（-5.602），被害人諒解的調節比例為-3.4%（-0.717），積極繳納罰金或財產保證的調節比例為-7.2%（-1.436），立功的調節比例為+15.4%（-2.796），退賠退贓的調節比例為 +13.5%（-0.69），坦白的調節比例為-27.9%（+1.591），累犯的調節比例為 +8.2%（+2.012）；前科的調節比例為-9.6%（+1.618）；其他從輕情節的調節比例為+39.1%（-2.099），其他從重情節的調節比例為 +64.5%（-2.994），攜帶工具的調節比例為-8.7%（+0.863）。〔25〕將所有交互效應項均納入方程后，得到的線性回歸方程為：3.259+0.000768×盜竊數額-3.679×初犯-0.828×被害人諒解-1.671×積極繳納罰金和財產保證-2.294×立功-0.257×退賠退贓+0.452×自首+0.682×坦白+1.305×前科+2.279×累犯+0.825×其他從輕情節-0.892×其他從重情節+0.580×攜帶工具+0.000453×初犯×盜竊數額-0.000026×被害人諒解×盜竊數額-0.000055×積極繳納罰金和財產保證×盜竊數額+0.000118×立功×盜竊數額-0.000104×退賠退贓×盜竊數額-0.000347×自首×盜竊數額-0.000214×坦白×盜竊數額-0.000074×前科×盜竊數額+0.000063×累犯×盜竊數額-0.00030×其他從輕情節×盜竊數額+0.000495×其他從重情節×盜竊數額-0.000067×攜帶工具×盜竊數額。

可以看到，將所有的交互效應項均納入方程后，會出現與理論矛盾的情況。例如，前科、攜帶工具的調節比例為負數，說明在該模型中該情節減輕刑期；可是前科、攜帶工具本是從重情節，卻從輕處罰，不符合理論設定。又如，立功、退賠退贓、其他從輕情節的調節比例為正數，說明在該模型中該情節增加刑期；可是立功、退賠退贓、其他從輕情節本是從輕情節，卻從重處罰，也不符合理論設定。所以并非所有的交互效應項都能夠被納入方程，即“比例固定”模式的理想的理論模型不能夠被獲取。

（2）兩種調節幅度模式的最優回歸方程的擬合

經過調整，在符合理論的從輕從重處罰原則的基礎上，模型中含有交互效應項的數目不同，模型調整R方也不相同。我們是取交互效應項數目最多的模型，還是取模型調整R方最大的模型呢？

從表面上看，我們的目的是比較“比例固定”與“數值固定”模型的優劣，而“比例固定”模式與“數值固定”模式的不同就在于有交互效應項，所以應當取交互效應項數目最多的模型，而非調整R方最大的模型。然而，我們比較“比例固定”與“數值固定”兩種模式優劣的目的，卻是為了找到可以更好地與司法實務數據相契合的調節幅度模式。也就是說，找到某種調節幅度模式，其預測宣告刑與實際宣告刑之間的“差的平方和”最小。而調整R方最大的模式，其預測宣告刑與實際宣告刑之間的“差的平方和”才是最小的。所以，在“比例固定”模式中，我們應當選取具有交互效應項的調整R方最大的模型，即“比例固定”模式的最優回歸方程；在“數值固定”模式中，我們應當選取沒有交互效應項的調整R方最大的模型，即“數值固定”模式的最優回歸方程。

（3）“準比例固定”模式取代純粹的“比例固定”模式

因為“比例固定”模式理想的理論模型不能夠被獲取，所以即使在引入交互效應項的最優回歸方程中，交互效應項的數目也不多。其中沒有交互效應項的量刑情節，仍然需要采取“數值固定”的調節幅度方法，從而導致有交互效應項的最優回歸方式，實際上是“部分比例固定、部分數值固定”的線性回歸方程。也就是說，現有的《量刑指導意見》中的“比例固定”模式在司法實踐中只能是“部分比例固定、部分數值固定”的調節幅度模式（簡稱為“準比例固定”模式）。

在比較兩個最優回歸方程后，若結論是“交互效應項有必要被引入”，則說明“準比例固定”模式更優越；若結論是“交互效應沒有必要被引入”，則說明“數值固定”模式更優越。

2.“準比例固定”模式和“數值固定”模式的比較

（1）兩種模式最優回歸方程的獲取

運用SPSS中一般線性回歸方法，利用盜竊數額為0～5萬元的770個記錄，盜竊數額為5萬元～40萬元的198個記錄，以及盜竊數額為40萬元及以上的40個記錄，得到表1的模型擬合系數。

（2）盜竊數額為0～5萬元的調節幅度模式比較

從表1可以看出，“準比例固定”模式中，“比例固定”的情節包括：被害人諒解、積極繳納罰金或財產憑證、退賠退贓、認罪態度、其他從重情節等；“數值固定”的情節包括：累犯、前科等。

從表1中還可以看出，“準比例固定”模式中，預測宣告刑與實際宣告刑差的平方和4 903.39，要小于“數值固定”模式中差的平方和5 684.18。并且殘差平方的均值檢驗中，其顯著性檢驗的sig值為0.036，小于0.05，具有顯著性。〔26〕顯著性檢驗的sig值小于0.05即具有顯著優勢。也即是說，“準比例固定”模式要優于純粹的“數值固定”模式。

（3）盜竊數額為5萬元～40萬元的調節幅度模式比較

用同樣的方法，得到表1中盜竊數額為5萬～40萬元的模型系數及殘差平方的均值檢驗結果。從表1中可以看出，“數值固定”模式中，預測宣告刑與實際宣告刑的差的平方和41 478.60，大于“準比例固定”模式中預測宣告刑與實際宣告刑的差的平方和21 855.07；并且，在殘差平方的均值檢驗中，其顯著性檢驗的sig值為0.006，小于0.05，具有顯著性。“準比例固定”模式比“數值固定”模式，從統計學上看具有顯著優勢。所以，對于盜竊數額為5萬元～40萬元的模型來說，引入交互效應項是有必要的，應當采取 “準比例固定”模式。

（4）盜竊數額為40萬元及以上的調節幅度模式比較

用同樣的方法，得到表1中盜竊數額為40萬元及以上的模型系數以及殘差平方的均值檢驗結果。從表1中可以看出，“數值固定”模式中，預測宣告刑與實際宣告刑的差的平方和10 007.01，大于“準比例固定”模式中預測宣告刑與實際宣告刑的差的平方和9 533.29；但是，在殘差平方的均值檢驗中，其顯著性檢驗的sig值為0.405，大于0.05，不具有顯著性。所以，“數值固定”模式與“準比例固定”模式之間沒有顯著差異，從統計學上看，兩者具有相同的優勢。所以，對于盜竊數額為40萬元及以上的模型來說，采取 “數值固定”模式更簡潔易行。

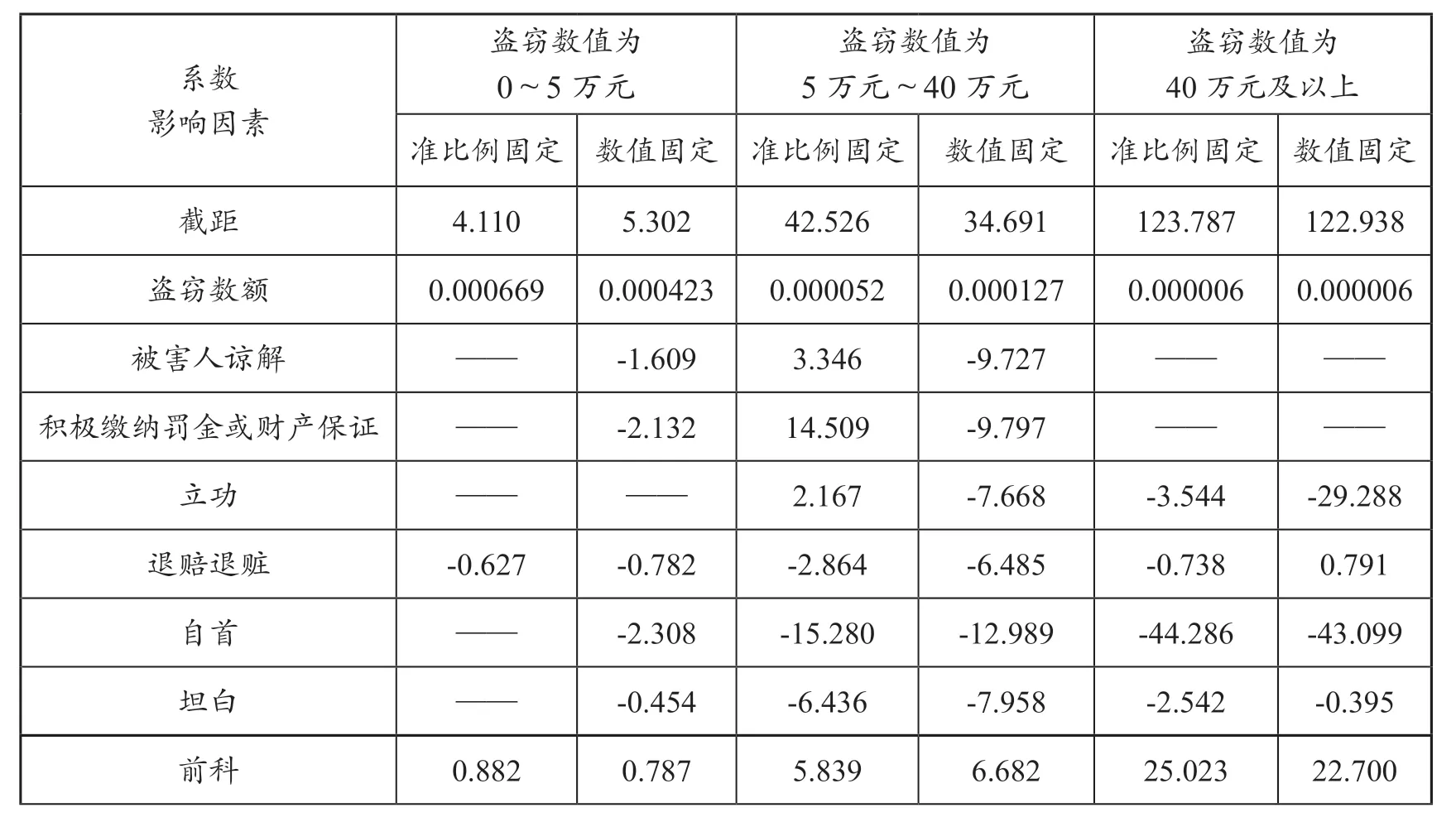
表1 準比例固定模式與數值固定模式的對比研究〔27〕對于一般線性回歸后，所有方程中均沒有納入的量刑影響因素，表格中不再列出。下文的表格均與此相同。

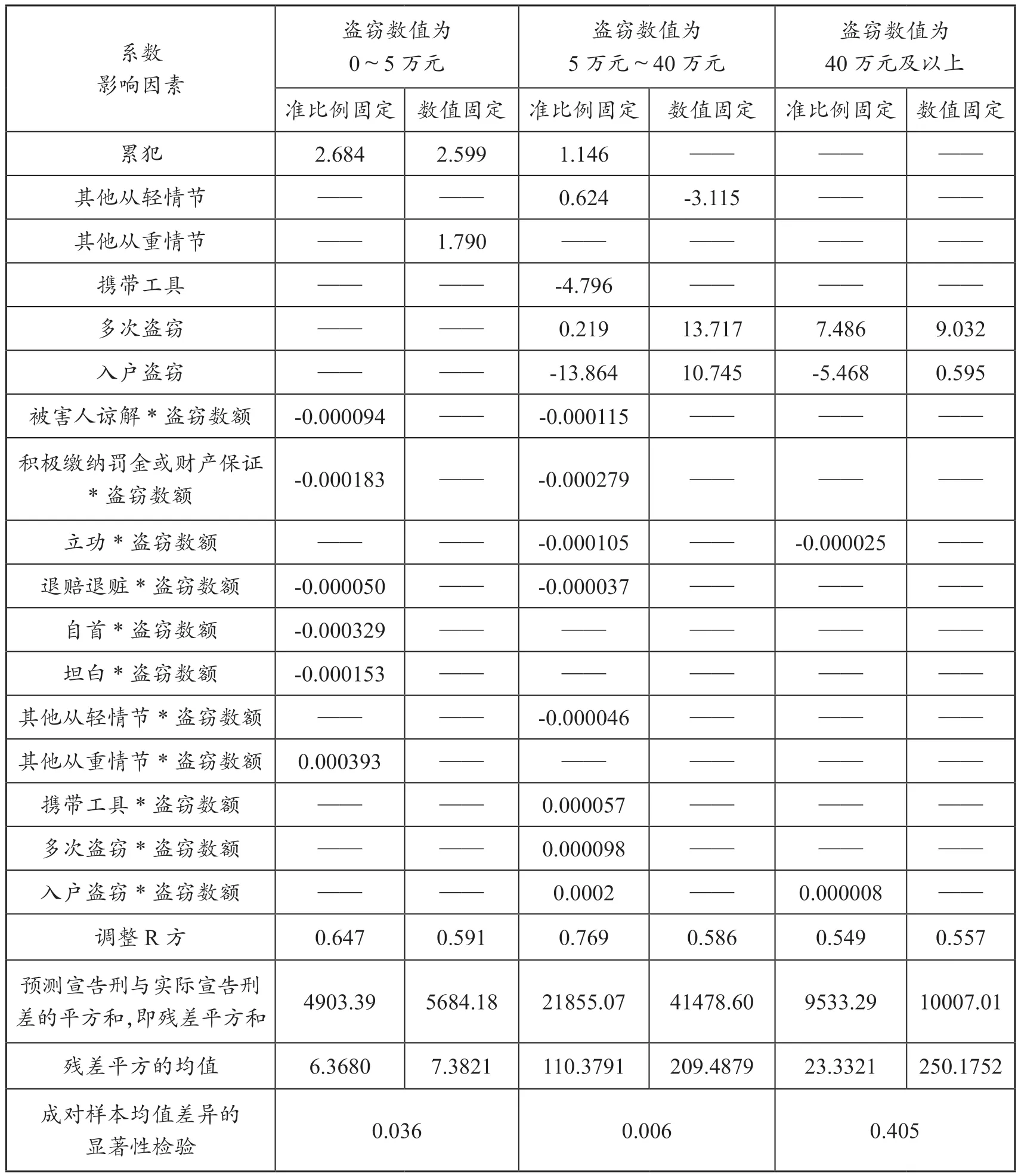
（續表）

3.具體調節比例和調節數值的計算

從表1中可以計算出盜竊數額為0～5萬元的“準比例固定”模式中調節比例的具體數值。被害人諒解的調節比例為-14.1%（+0.580），積極繳納罰金或財產憑證的調節比例為-27.4%（+1.126），退賠退贓的調節比例為-7.5%（-0.319），自首的調節比例為-49.2%（+2.022），坦白的調節比例為-22.9%（+0.941），其他從重情節的調節比例為58.7%（-2.413）。

對于“數值固定”的量刑情節來說，其調節幅度的固定數值，即為表1中該情節對應的回歸方程的系數，不需要另外計算。例如，在“準比例固定”模式中，累犯的調節數值為直接在基礎刑的基礎上加上+2.684個月，前科的調節數值為+0.882個月。

從表1中還可以計算出盜竊數額為5萬元～40萬元的調節數值。被害人諒解的調節比例為-221.15%（+97.392），積極繳納罰金或財產憑證的調節比例為-536.54%（+242.678），立功的調節比例為-201.92%（+88.035），退賠退贓的調節比例為-71.15%（+27.443），其他從輕情節的調節比例為-88.46%（-38.242），攜帶工具的調節比例為 109.62%（-51.413），多次盜竊的調節比例為 188.46%（-79.925），入戶盜竊的調節比例為384.62%（-177.428）。另外，還有一些情節是“數值固定”調節模式：自首的調節數值為-15.280，坦白的調節數值為-6.436，前科的調節數值為+5.839，累犯的調節數值為+1.146。

當然，從表1中也可以計算出盜竊數額為40萬元及以上的調節數值。即立功的調節數值為-29.288個月，退賠退贓的調節數值為-0.791個月，自首的調節數值為-43.099個月，坦白的調節數值為-0.395個月，前科的調節數值為+22.7個月，多次盜竊的調節數值為+9.032個月，入戶盜竊的調節數值為+0.595個月。

4.調節幅度模式比較的結論

總結表1的數據可以得出，對于盜竊數額為0～5萬元和5萬元～40萬元的最優回歸方程來說，有必要引入交互效應項；而對于盜竊數額為40萬元及以上的最優回歸方程說，沒有必要引入交互效應項。也就是說，對于盜竊數額為0～5萬元和5萬元～40萬元的犯罪來說，“準比例固定”模式要優于純粹“數值固定”模式；而對于盜竊數額為40萬元及以上的犯罪來說，“數值固定”模式更為可取。

可見，不同的情況下，調節基準刑的模式不同。有的時候是比例固定，有的時候是數值固定，而非“一刀切”地“比例固定”或者“數值固定”。即使在盜竊數額為0～5萬元和5萬元～40萬元的最優回歸方程中，有的情節是“比例固定”模式，而有的情節是“數值固定”模式。

另外，一般來說，純粹的“比例固定”調節方式并不可取，因為這種模式會導致量刑情節對基準刑的調節幅度不符合理論上從輕從重處罰原則的要求。

三、調節程式的實證研究

在得出調節幅度必須兼顧“準比例固定”和“數值固定”兩種模式的基礎上，利用上述2 355個盜竊罪記錄來比較調節程式中復合模式與單一模式的優劣。

（一）案例選擇

首先，選擇包含“從犯”情節，但還不包含未成年及限制行為能力情節和從犯情節的案件。兩種調節程式的比較必須包含“未成年犯罪、老年犯罪、限制行為能力的精神病人犯罪、又聾又啞的人或者盲人犯罪、防衛過當、避險過當、犯罪預備、犯罪未遂、犯罪中止、從犯、脅從犯、教唆犯”等情節中的一個或者多個。本文的數據中包含了未成年或限制行為能力人犯罪、犯罪未遂、從犯這三種情節。如果將三種情節同時納入考慮將導致回歸方程十分復雜，為了比較研究更容易，本文選擇只包含“從犯”這一個情節的案例，共有2 209個記錄。

其次，為了比較研究更容易實行，本文只考慮以“盜竊數額”為基準事實的情況下，量刑情節對基準刑的調節方法。理想狀態下應當選擇沒有“扒竊、多次盜竊、入戶盜竊、攜帶兇器盜竊”情節的案例。但是，若將包含上述情節案例全部刪除，最后剩下的含有“從犯”情節的案例會很少，導致本文帶有“連乘法”的復合模式無法實現。所以，我們選擇了折中的方法，在盜竊數額為0～5萬元及5萬元～40萬元時，刪除含有多次盜竊、攜帶兇器盜竊的案例，而保留具有“扒竊、入室盜竊”量刑情節的案例；在盜竊數額為40萬元及以上時，保留所有多次盜竊、攜帶兇器、扒竊、入室盜竊的案例。

最后，因變量的刑罰種類中，本文只選擇有期徒刑和拘役兩種。因為單處罰金和管制并沒有統一折算的方法，加之記錄數量較少，所以予以刪除。剩下盜竊數額為0～5萬元的記錄1 204個，盜竊數額為5萬元～40萬元的記錄102個，盜竊數額為40萬元及以上的記錄51個。

（二）兩種調節程式的理論模型

上述1 357個記錄中，除盜竊數額、從犯外，量刑情節還包括初犯、被害人諒解、積極繳納罰金或財產保證、立功、退贓退賠、認罪態度、前科、累犯、其他從輕情節、其他從重情節、多次盜竊、攜帶工具、入室盜竊、扒竊等。值得注意的是，對于盜竊數額為5萬元～40萬元，以及40萬元及以上的情況，本文刪除了影響因素頻次小于5的影響因素，不納入一般線性回歸。〔28〕因為如果原有影響因素的記錄數就小于5個，那么當該影響因素與其他因素形成交互作用項時，該交互作用項的記錄更少，甚至為0，這樣導致一般線性回歸系數異常，所以予以刪除。

1.復合模式的理論模型

復合模式的刑罰量計算公式為：盜竊罪拘役刑或徒刑刑期=（b0+b1×盜竊數額）×（1+b2×從犯）×（1+a1×初犯+a2×被害人諒解+a3×積極繳納罰金或財產保證+a4×立功+a5×退贓退賠+a6×認罪態度+a7×前科+a8×累犯+……+a15×扒竊）=b0+b1×盜竊數額+c0×從犯+c1×初犯+c2×被害人諒解+c3×積極繳納罰金或財產保證+c4×立功+c5×退賠退贓+c6×認罪態度+c7×前科+……+c15×扒竊+d0×從犯×盜竊數額+d1×初犯×盜竊數額+d2×被害人諒解×盜竊數額+d3×積極繳納罰金或財產保證×盜竊數額+d4×立功×盜竊數額+d5×退贓退賠×盜竊數額+d6×認罪態度×盜竊數額+d7×前科×盜竊數額+d8×累犯×盜竊數額+……+d15×扒竊×盜竊數額+e1×初犯×從犯+e2×被害人諒解×從犯+e3×積極繳納罰金或財產保證×從犯+e4×立功×從犯+e5×退贓退賠×從犯+e6×認罪態度×從犯+e7×前科×從犯+e8×累犯×從犯+……+e15×扒竊×從犯+f1×初犯×從犯×盜竊數額+f2×被害人諒解×從犯×盜竊數額+f3×積極繳納罰金或財產保證×從犯×盜竊數額+f4×立功×從犯×盜竊數額+f5×退贓退賠×從犯×盜竊數額+f6×認罪態度×從犯×盜竊數額+f7×前科×從犯×盜竊數額+f8×累犯×從犯×盜竊數額+……+f15×扒竊×從犯×盜竊數額。

可以看出，這一理論模型拆分為一般線性回歸方程后，共有64個相加項，其中交互效應項最多包含三個量刑情節。這還是只有一個“修正量刑情節”的情況。如果有兩個“修正量刑情節”，拆分后將有128個相加項，其復雜程度可想而知。

2.單一模式的理論模型

如第二部分所證明的那樣，在單一模式的情況下，必須兼顧“準比例固定”模式和“數值固定”模式。因為，“準比例固定”模式和“數值固定”模式均可以用帶有交互效應項回歸方程來表示，只是“數值固定”模式的方程中交互效應項的系數為零，而“準比例固定”的方程中交互效應項的系數不全部為零。所以，對于單一模式的回歸方程，我們仍然按照“準比例固定”模式的回歸方程，只是在必要的時候將交互效應項的系數設置為零即可。

可見，單一模式的理論模型為：盜竊罪拘役刑或徒刑刑期=（B0+B1×盜竊數額）×（1+A0×從犯+A1×初犯+A2×被害人諒解+A3×積極繳納罰金或財產保證+A4×立功+A5×退贓退賠+A6×認罪態度+A7×前科+A8×累犯+……+A14×扒竊）=B0+B1×盜竊數額+C0×從犯+C1×初犯+C2×被害人諒解+C3×積極繳納罰金或財產保證+C4×立功+C5×退贓退賠+C6×認罪態度+C7×前科+C8×累犯+……+C15×扒竊+D0×從犯×盜竊數額+D1×初犯×盜竊數額+D2×被害人諒解×盜竊數額+D3×積極繳納罰金或財產保證×盜竊數額+D4×立功×盜竊數額+D5×退贓退賠×盜竊數額+D6×認罪態度×盜竊數額+D7×前科×盜竊數額+D8×累犯×盜竊數額+……+D15×扒竊×盜竊數額。

（三）最優調節程式的獲取方法

利用盜竊罪的司法數據，根據上述兩個理論模型擬合出兩個最優回歸線性方程。而要比較這兩個最優線性回歸方程中哪個更具有實踐優勢，需要用“均值比較”方法進行檢驗。

檢驗的具體步驟如下：首先，利用“一般線性回歸”方法計算出上述兩個理論模型的最優回歸方程的系數；其次，計算出兩個最優回歸方程下的預測宣告刑的數值；再次，計算兩個預測宣告刑與實際宣告刑的差的平方和，即殘差平方和，殘差平方和小的方法效果最佳；最后，還需要檢驗上述預測宣告刑與實際宣告刑之間的殘差平方是否具有顯著性差異。檢驗顯著性的方法仍然是成對的均值比較方法。具有顯著優勢的回歸方程，即為最優調節程式。

（四）一般線性回歸方程的結果分析

1.復合模式和單一模式中最優回歸方程的獲取

根據盜竊數額為0～5萬元的1 204個記錄，和盜竊數額為5萬元～40萬元的102個記錄及盜竊數額為40萬元及以上的51個記錄，用SPSS中的一般線性回歸方法，可以得到表2中的三組六個最優回歸方程。

2.盜竊數額為0～5萬元的調節程式比較

根據表2的數據可知，對于盜竊數額為0～5萬元來說，復合模式的殘差平方和9 826.73，小于單一模式的殘差平方和9 961.97。但是，殘差平方的均值檢驗中，其顯著性檢驗的sig值為0.263，大于0.05，不具有顯著性。也就是說，兩種調節程式沒有顯著差異。復合模式并不優越于單一模式。從而，復合模式應當被排除，單一模式更可取。

3.盜竊數額為5萬元～40萬元的調節程式比較

根據表2的數據可知，對于盜竊數額5萬元～40萬元來說，復合模式的殘差平方和12 752.03，小于單一模式的殘差平方和13 422.11。但是，殘差平方的均值檢驗中，其顯著性檢驗的sig值為0.241，大于0.05，不具有顯著性。也就是說，兩種調節程式沒有顯著差異。復合模式并不優越于單一模式。從而，復合模式應當被排除，單一模式更可取。

4.盜竊數額為40萬元及以上的調節程式比較

根據表2的數據可知，對于盜竊數額40萬元及以上來說，復合模式的殘差平方和17 237.91，大于單一模式的殘差平方和16 335.36。但是，殘差平方的均值檢驗中，其顯著性檢驗的sig值為0.726，大于0.05，不具有顯著性。也就是說，兩種調節程式沒有顯著差異。復合模式并不優越于單一模式。從而，復合模式應當被排除，單一模式更可取。

5.盜竊數額為0～5萬元時兩種調節程式中調節幅度的計算〔29〕盜竊數額為5萬元～40萬元以及40萬元及以上的情況下，其調節幅度的計算方法和本節一致。由于篇幅限制，不再一一計算。

還原表2中盜竊數額0～5萬元的一般線性回歸方程，可以得到單一模式的回歸方程為：盜竊罪拘役刑或徒刑刑期=（4.542+0.000549×盜竊數額）（1-0.317×從犯-0.317×自首-0.046×坦白-0.149×被害人諒解+0.233×累犯-0.683×其他從輕情節+0.696×其他從重情節+0.04×入室盜竊）+1.082×從犯+0.569×自首-0.308×坦白-0.183×被害人諒解+1.369×累犯+5.128×其他從輕情節-3.571×其他從重情節+0.854×入室盜竊-1.042×立功-1.715×積極繳納罰金或財產保證-0.640×退賠退贓+0.730×前科+0.285×攜帶工具+1.014×扒竊。

從上式可以得出，利用1 204個記錄得到的盜竊數額為0～5萬元的單一模式中，各量刑情節的調節比例和數值如下：從犯為-31.7%（+1.082），自首為-31.7%（+0.569），坦白為-4.6%（-0.308），被害人諒解為-14.9%（-0.183），累犯為 +23.3%（+1.369），其他從輕情節為-68.3%（+5.128），其他從重情節為+69.6%（-3.571），入室盜竊為+4.0%（+0.854）。其他量刑情節為“固定數值”的調節幅度：立功為（-1.042），積極繳納罰金或財產保證為（-1.715），退賠退贓為（-0.640），前科為（+0.730），攜帶工具為（+0.285），扒竊為（+1.014）。所有數值的單位均為月。

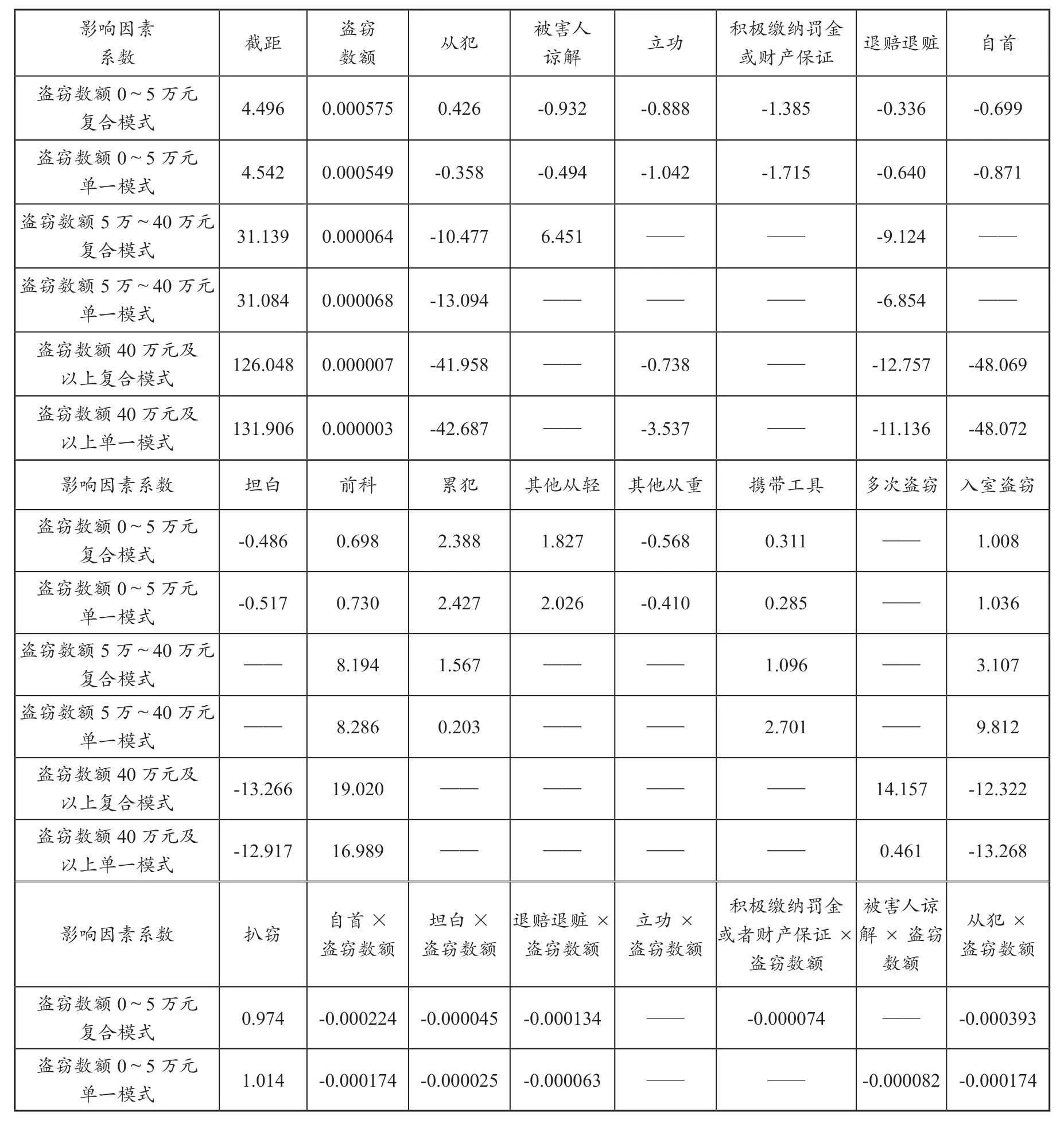
表2 復合模式與單一模式對比研究

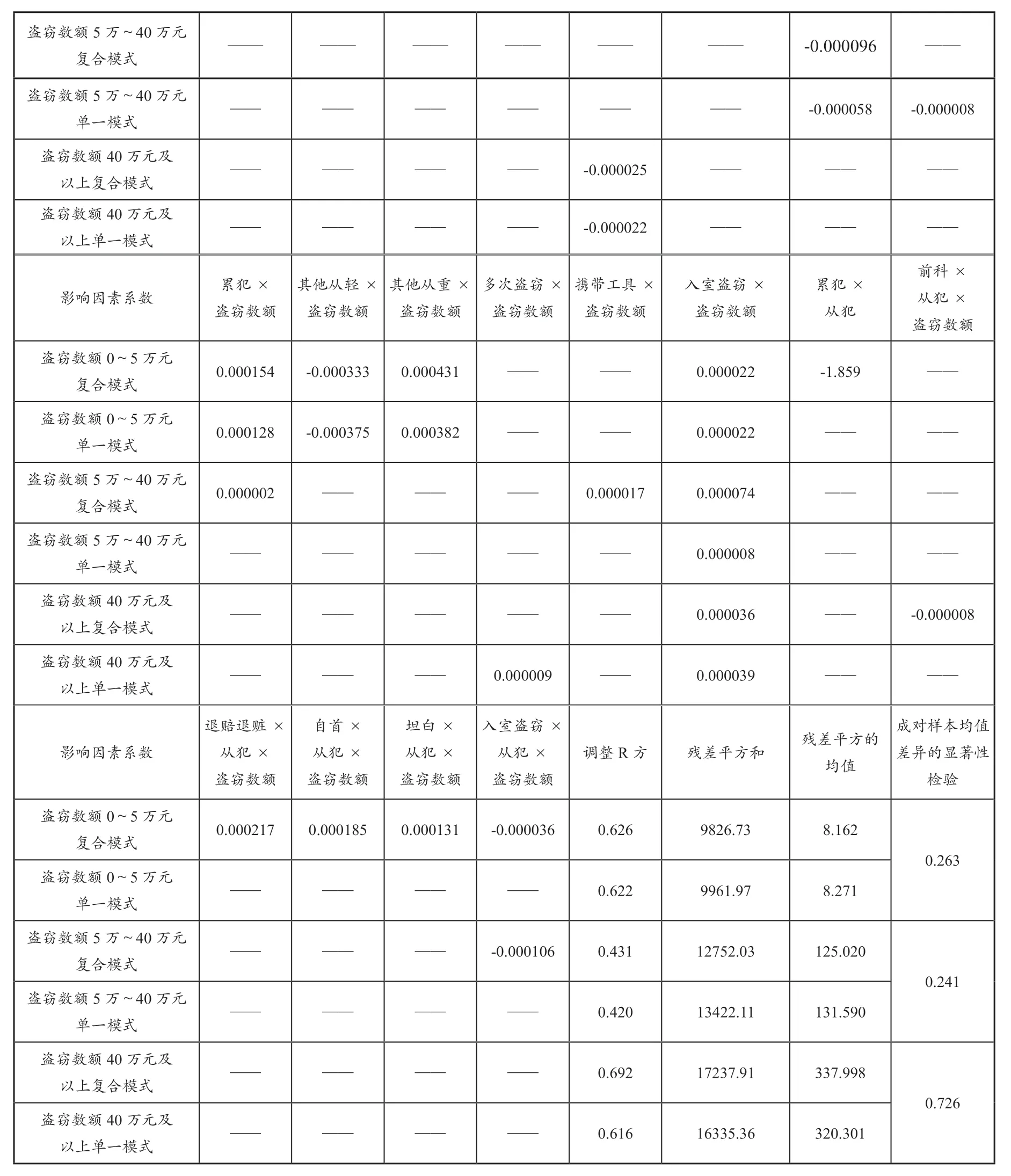
（續表）

同理，還原表2中的回歸方程，可以得到盜竊數額為0～5萬元的復合模式的調節程式為：盜竊罪拘役刑或徒刑刑期=（4.496+0.000575×盜竊數額）（1-0.683×從犯）（1-0.557×退贓退賠-0.005×自首-0.334×坦白+0.092×入室盜竊）+（4.496+0.000575×盜竊數額）（+0.323×退贓退賠-0.384×自首+0.256×坦白-0.050×入室盜竊-0.129×積極繳納罰金或財產保證+0.268×累犯-0.579×其他從輕情節+0.750×其他從重情節）+0.716×退贓退賠+1.409×自首-0.135×坦白+0.819×入室盜竊-0.803×積極繳納罰金或財產保證+1.183×累犯+4.430×其他從輕情節-3.122×其他從重情節-0.932×被害人諒解-0.888×立功+0.698×前科+0.311×攜帶工具+0.974×扒竊-1.710×退贓退賠×從犯-0.015×自首×從犯-1.026×坦白×從犯+0.283×入室盜竊×從犯-1.859×累犯×從犯。

從上面的回歸方程還原式可以看出，只有一部分量刑情節（這里包括退贓退賠、認罪態度、入室盜竊情節）能夠被納入連乘式中。大部分量刑情節必須通過“比例固定”和“數值固定”相結合的單一模式對基準刑進行調節。

（五）調節程式比較的結論

本文的數據顯示，在盜竊數額為0～5萬元的盜竊罪中，以及盜竊數額為5萬元～40萬元和40萬元及以上的盜竊罪中，復合模式均沒有明顯優于單一模式。所以，現有的《量刑指導意見》中的復合調節程式并不具有優越性，不可取。

四、基準刑調節方法的完善

本文主要討論基準刑調節方法的完善，但會涉及量刑情節的區分和選取，以及基準刑的確定，因為這些內容將影響到基準刑調節方法的確定。

（一）確立“比例固定”與“數值固定”相結合的調節幅度模式

根據實證分析，通過兩種調節幅度模式的比較，可以得出如下結論。

1.純粹的“比例固定”模式不可取

第二部分和第三部分的數據顯示，純粹“比例固定”模式不能與理論上從輕從重的處罰原則契合。

如前所述，當用第二部分的盜竊數額為0～5萬元的770個盜竊罪記錄進行一般線性回歸，將所有交互效應項都納入回歸方程時，前科、攜帶工具本是從重情節，卻從輕處罰；而立功、退賠退贓、其他從輕情節本是從輕情節，卻從重處罰。所以純粹的“比例固定”模式不可取。

2.“準比例固定”模式與“數值固定”模式處于并存狀態

表1的數據得出，對于盜竊數額為0～5萬元和5萬元～40萬元的犯罪來說，“準比例固定”的模式要優于純粹“數值固定”的模型，而對于盜竊數額為40萬元及以上的犯罪來說，“數值固定”模型更為可取。表2的數據可以看出，在盜竊數額為0～5萬元、5萬元～40萬元以及40萬元及以上的犯罪中，單一模式的表現形式也是 “準比例固定”模式。可見，“準比例固定”模式雖然是主要的調節幅度模式，但是“數值固定”模式也在有的調節幅度和調節情節中得到應用。

根據司法數據的不同，“準比例固定”模式與“數值固定”模式均可能成為最優調節幅度模式。所以，建議將來《量刑指導意見》中的調節幅度模式不要“一刀切”地采取某一種模式，而應根據司法數據，分情況制定不同的模式。

3.調節比例與調節數值的計算

調節幅度模式應當采取“比例固定”和“數值固定”相結合的方法。但問題是，哪些量刑情節采取“比例固定”方法，哪些量刑情節采取“數值固定”方法，以及具體的調節比例和調節數值如何確定。

（1）盜竊數額為0～5萬元的犯罪中調節比例和調節數值的確定

本文共得到兩個盜竊數額為0～5萬元的最優回歸方程：一個是樣本量為770個記錄的表1中“準比例固定”模式的最優回歸方程；一個是樣本量為1 204個記錄的表2中單一模式的最優回歸方程。這兩個最優回歸方程得到的各個量刑情節的調節比例和調節數值并不相同。表1中“準比例固定”模式的最優回歸方程得到數據為：被害人諒解的調節比例為-14.1%（+0.580），積極繳納罰金或財產保證的調節比例為-27.4%（+1.126），退賠退贓的調節比例為-7.5%（-0.319），自首的調節比例為-49.2%（+2.022），坦白的調節比例為-22.9%（+0.941），其他從重情節的調節比例為58.7%（-2.413），累犯的調節數值為+2.684個月，前科的調節數值為+0.882個月。

表2中單一模式的最優回歸方程得到各量刑情節的調節比例和數值如下：從犯為-31.7%（+1.082），自首為-31.7%（+0.569），坦白為-4.6%（-0.308），被害人諒解為-14.9%（-0.183），累犯為+23.3%（+1.369），其他從輕情節為-68.3%（+5.128），其他從重情節為 +69.6%（-3.571），入室盜竊為+4.0%（+0.854）。其他量刑情節為“固定數值”的調節幅度：立功為（-1.042），積極繳納罰金或財產保證為（-1.715），退賠退贓為（-0.640），前科為（+0.730），攜帶工具為（+0.285），扒竊為（+1.014）。

對比兩個最優回歸方程的調節比例和調節數值，發現同一量刑情節的調節幅度模式、調節幅度數據均不相同。那么，如何確定一個犯罪中，各個量刑情節對基準刑的調節幅度模式和調節幅度數據呢？

對于調節幅度模式，應當選擇多數最優回歸方程得到的模式。如上述兩個最優回歸方程中，累犯的調節方式不相同。表1的調節模式為“數值固定”模式，調節數據為（+2.684）個月。表2的調節幅度模式為 “準比例固定”模式，調節數據為+23.3%（+1.369）個月。在只有兩個最優回歸方程的情況下，我們當然不好選擇“準比例固定”模式還是“數值固定”模式。但是，當我們進行多次回歸后，得到多個最優回歸方程的情況下，就可以選擇多數最優回歸方程得到的調節幅度模式。假設，我們對盜竊數據為0～5萬元的數據進行了10次一般線性回歸，從而得到10個最優回歸方程。這10個最優回歸方程中，有7個最優回歸方程中，累犯均采取“準比例固定”調節幅度模式，那么，我們就認為，在0～5萬元的盜竊罪中，累犯應當選擇“準比例固定”調節幅度模式。

確定好調節幅度模式后，調節幅度數據則應當根據所有數據的均值進行確定。例如，上述兩個最優回歸方程中，被害人諒解的調節幅度數據分別為-14.1%（+0.580）個月和-14.9%（-0.183）個月。那么，我們最終確定0～5萬元盜竊罪中，被害人諒解的調節幅度數據則為兩者的平均值，即-14.5%（+0.197）個月。當然，通常我們需要用多個最優回歸方程的數據來進行平均數的計算，而非兩個最優回歸方程的數據。

假設，我們分別用10組不同的數據對盜竊罪0～5萬元的最優回歸方程進行擬合，得到10個最優回歸方程。其中7個顯示，被害人諒解的調節幅度應當為“準比例固定”模式，且7個數據分別 為 -14.1%（+0.580）、-14.9%（-0.183）、-33.1%（+1.235）、-26.5%（+3.075）、-44.8%（-3.671）、-29.8%（+2.873）、-38.6%（+3.280）。那么，我們可以得出結論，盜竊數額為0～5萬元的盜竊行為中，被害人諒解的調節幅度應當采取“準比例固定”模式，其調節比例為上述7個數據的平均值，即-28.8%（+1.027）。

（2）不同法定刑幅度、不同罪名中同一量刑情節調節幅度的確定

用上面的方法可以確定同一罪名同一法定刑幅度中同一量刑情節的調節幅度。那么，同一罪名中，不同法定刑幅度，或者不同罪名中，同一量刑情節的調節幅度如何確定呢？它們的調節幅度是否固定不變呢？

如果通過多次線性回歸得到的多個最優回歸方程中，不同法定刑幅度、不同罪名中同一量刑情節調節幅度的均值處于比較集中的數據段，那么可以確定這一數據段為同一量刑情節的固定調節幅度。如果不同幅度、不同罪名中，同一量刑情節調節幅度的均值處于很分散的數據段，那么不能確定它們具有固定的調節幅度，而應該各自確定它們的調節幅度。

（二）調節幅度需要受到責任刑上限的制約

我國量刑規范化形成了一個基本的共識，即刑罰的裁量不能超過責任刑的上限，這是責任主義的基本要求。〔30〕參見張明楷：《責任主義和量刑原理——以點的理論為中心》，載《法學研究》2010年第5期；姜濤：《責任主義與量刑規則：量刑原理的雙重體系建構》，載《政治與法律》2014 年第3期；李冠煜：《量刑規范化改革視野下的量刑基準研究》，載《比較法研究》2015年第6期。

1.責任刑上限對調節幅度的限制是刑法學界共識

關于責任刑與預防刑的關系，量刑理論上有點的理論與幅的理論之爭。但是，不管是“點的理論”還是“幅的理論”都認可責任刑上限對刑罰幅度的限制。在日本，持有“點的理論”的見解認為，應該在量刑時把行為人的責任作為“上限”，在不超出其范圍內，從預防性考慮出發來決定最終刑；持有“幅的理論”的見解認為，把行為人的責任作為量刑“基礎”的同時，原則上應該在責任評價的“幅度”內，或者不太脫離責任，加入預防性的考慮來決定最終刑。〔31〕參見［日］城下裕二：《量刑理論的現代課題》增補版，黎其武、趙珊珊譯，法律出版社2016年版，第4頁。德國認同“點的理論”的學者也指出，在罪責抵償與個別預防相矛盾時，必須認為，在正確遵守所有法律上的和事實上的規定的情況下，恰恰有一個與每一個行為的嚴重程度相適應的特定的刑罰。而德國判例則認可“幅的理論”，認為為了達到罪責抵償和特殊預防之間的平衡和協調，不能具體規定與案件的罪責相適應的刑罰，而只是規定一個刑罰幅度，這一幅度以刑罰能夠實現其公正的罪責抵償的任務為限，然后，再根據刑罰對行為人的再社會化所期望的效果，在罪責的幅度之間確定刑罰。〔32〕參見［德］漢斯·海因里希·耶塞克、托馬斯·魏根特：《德國刑法教科書》，徐久生譯，中國法制出版社2001年版，第1051-1052頁。我國學者張明楷教授也指出，責任刑上限點對刑罰幅度的限制，體現了刑法的人權保障機能與法益保護機能的協調關系。〔33〕參見張明楷：《責任刑與預防刑》，北京大學出版社2015年版，第155頁。

2.責任刑上限對調節幅度限制的實現

要實現責任刑上限對調節幅度的制約，只需要在現有量刑步驟的基礎上，增加幾個特定的步驟即可。

首先，我們可用責任刑情節調節基準刑，形成責任刑上限。其次，用預防刑情節在責任刑上限的基礎上，調節基準刑，形成準宣告刑。最后，用準宣告刑與責任刑上限對比，若準宣告刑在責任刑上限之下，則直接將準宣告刑作為宣告刑；若準宣告刑高于責任刑上限，將責任刑上限作為宣告刑。

這一量刑理論和步驟體現在量刑公式中即為：刑罰量=基準刑×（1+責任刑情節1的調節比例+……+責任刑量刑情節n的調節比例）+（從重責任刑情節的調節數值-從輕責任刑情節的調節數值）+基準刑×（1+預防刑情節1的調節比例……+預防刑量刑情節n的調節比例）+（從重預防刑情節的調節數值-從輕預防刑情節的調節數值）。在具體計算時，先計算出前面責任刑情節的數值，再計算總的數值，然后拿總的數值與責任刑情節的數值比較，取較小的那一個即可。

例如，表2中盜竊數額為0～5萬元的單一模式模型，可以表述為：盜竊罪拘役刑或徒刑刑期=（4.542+0.000549×盜竊數額）×（1-0.317×從犯+0.04×入室盜竊）+（1.082×從犯+0.854×入室盜竊+0.285×攜帶工具+1.014×扒竊）+（4.542+0.000549×盜竊數額）×（-0.317×自首-0.046×坦白-0.149×被害人諒解+0.233×累犯-0.683×其他從輕情節+0.696×其他從重情節）+（0.569×自首-0.308×坦白-0.183×被害人諒解+1.369×累犯+5.128×其他從輕情節-3.571×其他從重情節-1.042×立功-1.715×積極繳納罰金或財產保證-0.640×退賠退贓+0.730×前科）。因為從犯、攜帶工具、入室盜竊、扒竊等均為責任刑情節，所以先計算出算式（4.542+0.000549×盜竊數額）×（1-0.317×從犯+0.04×入室盜竊）+（1.082×從犯+0.854×入室盜竊+0.285×攜帶工具+1.014×扒竊）的數值，作為責任刑上限，然后再計算出整個算式的數值，將之與上述責任刑上限作比較，取較小的一個作為宣告刑即可。

就具體案例來說，上述單一模式可以表述如下。例如，（案例8）某盜竊罪案例中，行為人盜竊4萬元，且存在從犯、自首、被害人諒解三個情節，則盜竊罪拘役刑或徒刑刑期=（4.542+0.000549×盜竊數額）×（1-0.317×從犯）+1.082×從犯+（4.542+0.000549×盜竊數額）×（-0.317×自首-0.149×被害人諒解）+（0.569× 自首-0.183× 被害人諒解）=（4.542+0.000549×40000）×（1-0.317）+1.082+（4.542+0.000549×40000）×（-0.317-0.149）+0.569-0.183=19.183-11.964=7.219。也就是說，行為人的責任刑是19.183個月，而行為人的準宣告刑是7.219個月，所以應當對行為人處以7.219個月。

（三）確立單一模式的調節程式

1.理論上復合模式應當被排除

在盜竊罪中，量刑情節調節基準刑的調節程式應排除復合模式，選擇單一模式，原因如下。

（1）如本文第三部分所示，司法實證數據并沒有得出復合模式比單一模式具有顯著優勢，所以應當排除復合模式的適用。

（2）復合模式中的連乘法使基準刑處于不斷變動中，導致基準刑失去“基準”的意義。如第一部分所述，復合模式的連乘法使得基準刑在“修正量刑情節”的調節下處于不斷減輕的變動中。這種變動雖然使復合模式符合“罪行輕重不同的被告人如果具有相同的量刑情節，從輕的幅度相同但從輕的刑期可以不同”的量刑規律，但是出現了降低“修正量刑情節”的影響，有違反立法本意的弊端。

（3）復合模式的連乘法使得基準刑在“修正量刑情節”的調節下處于不斷減輕的變動中，隔斷了一般量刑情節對基準刑的直接作用。

（4）復合模式的連乘法產生了多項交互效應項，將修正犯罪構成量刑情節與一般量刑情節相互關聯、相互作用、相互影響，使得問題復雜化。

2.司法實踐中單一模式較易被接受

廈門中院的司法實踐認為單一模式與復合模式相比較，具有明顯的優勢，更符合當前審判實際的需要。主要體現在：第一，單一模式在基準刑的確定上簡便清晰。復合模式下基準刑的確定還要考慮未遂、從犯、防衛過當等所謂社會危害性情節，不但煩瑣復雜，而且容易造成基準刑變動不居的狀態。而單一模式下基準刑的確定，僅以基本犯罪事實的擬制既遂狀態為依據，不必考慮未遂、從犯等因素對基準刑的影響，使得基準刑確定較為簡便清晰，不易產生變數。第二，單一模式因其簡便易行更容易為法官所接受。統計數據表明，分別采取兩種量刑模式進行試點的思明區法院與集美區法院，因同一時期、同一法院的量刑基本保持均衡，試點前期案件的上訴率、發改率等審判績效并無明顯的差異；而針對法官的問卷調查則表明，單一模式的量刑步驟與傳統量刑思路相銜接，操作簡便，得到了大多數法官特別是基層法官的認同。〔34〕參見李志遠、黃冬陽：《從對立到統一 ——廈門中院量刑規范化改革之路徑選擇》，載《中國審判新聞月刊》 2009年第41期。