基于屈服等值線模型的巷道沖擊地壓發生判斷
孫中光
(1.瓦斯災害監控與應急技術國家重點實驗室,重慶 400037;2.中煤科工集團重慶研究院有限公司,重慶 400039;3.重慶大學 煤礦災害動力學與控制國家重點實驗室,重慶 400044)
沖擊地壓問題是困擾采礦與巖石工程界的一個突出問題,隨著我國礦山開采深度和開采強度不斷加大,礦井沖擊地壓危險也日趨嚴峻和復雜[1-5]。業內學者先后提出了一系列沖擊地壓觸發理論,主要包括強度理論、剛度理論、能量理論、沖擊傾向性理論、“三準則”理論、“三因素”理論、失穩理論及動靜載荷疊加理論等[6-15],分別從不同角度對沖擊地壓發生的條件和過程進行了系統的研究和論證。其中,姜耀東等[5]建立了煤礦沖擊地壓的3種力學模型,即材料失穩型、滑移錯動型和結構失穩型沖擊地壓。由于沖擊地壓發生機理復雜、影響因素較多,目前針對沖擊地壓的發生及防治機理的認識仍然不夠深入,沖擊地壓事故依然時有發生。
筆者基于材料失穩型沖擊地壓發生的特點,以煤巖石屈服為研究對象,建立巷道受力力學模型,通過屈服準則解釋巷道的圍巖由彈性向塑性轉化的趨勢過程,得到巷道沖擊地壓發生的參考判斷方法。
1 雙屈服等值線模型分析
1.1 屈服應力場分析
考慮煤礦層狀沉積巖覆巖的特性和頂底板的摩擦約束作用,選取矩形巷道側壁為研究對象,將巷道側壁簡化為端部受約束的壓縮體,半無限大板受力示意圖如圖1所示(圖中θ為任意點A和荷載作用點連線與荷載方向的夾角,(°);L為荷載作用點間的距離,m;l為板厚(巷幫煤柱高度),m;r1、r2分別為任意點A與荷載作用點連線長度,m)。

圖1 半無限大板受力示意圖
端部約束可以認為集中力P作用于巷道上下兩端,采用Airy應力函數計算。
表示A點受力的Airy函數Φ如下:
(1)
A點各應力分量如下:
(2)
采用莫爾圓將極坐標轉換為直角坐標,則x、y方向上的應力如下:
(3)
若2個集中應力的負載相同,則2個集中應力可以采用彈性力學疊加原理,對式(3)進行轉化,笛卡爾坐標系中點A的應力如下:
(4)
巷道開挖后,煤體向掘進空間膨脹,假設頂、底板巖石具有相同的特征,因此修正應力使其在y=0時,使應力σx一集中力分量為常數,并調整參數2P/πl。為滿足應力量綱的常量Q,引入系數QA表示豎直方向的壓縮力σy,A為無量綱系數,則式(4)可改寫為:
(5)
1.2 屈服趨勢分析
假設煤體服從莫爾-庫侖屈服準則,不平衡力F的屈服函數可以表示為:
(6)
式中:σ1為中間主應力,MPa;σ3為圍壓,MPa;C為黏聚力,MPa;φ為內摩擦角,(°);K為判別因子。
當不平衡力F≥K時,煤體將發生屈服破壞,而K值取決于材料本身的性質。將σx、σy和τxy代入式(6),可得:
AQ≥K=2Ccotφ(1-sinφ)-1
(7)
將有關參數值代入式(7),計算得到屈服函數等值線如圖2所示(不平衡力F范圍0.0~1.0,F為1.0時表示達到屈服極限)。

(a)φ=40°, C=3.2 MPa
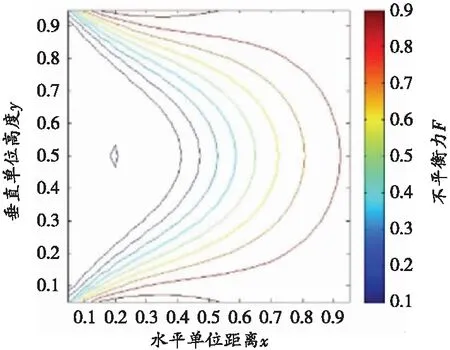
(b)φ=37°, C=(2.4x)MPa

(c)φ=40°, C=(2.4x)MPa

(d)φ=45°, C=(2.4x)MPa
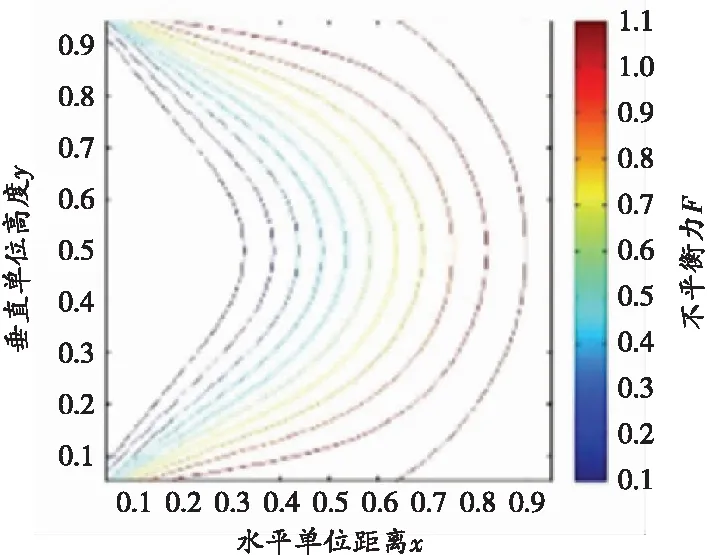
(e)φ=50°, C=(2.4x)MPa
若豎直應力為均布荷載(即C=3.2 MPa),內摩擦角φ取40°,將C值代入式(7),用Matlab計算屈服函數F在笛卡爾坐標系里呈現出類雙曲線的形式,如圖2(a)所示,可以看出,屈服函數等值線最大F值出現在靠近巷道外緣的部分,說明煤體在受力過程中會由外到內逐層破壞。
在煤礦地應力實測中,最大水平主應力為豎直應力的1.2~2.0倍[16-18](以1.5倍為例),式(5)中水平應力取值為(0,2Q)。巷道或工作面中實測豎直應力集中系數取2.0~4.0(以3.0為例),假設在應力增高區域的垂直應力呈線性逐漸升高,校正系數取為0.6,故C值為:
C=2÷1.5×0.6×3x=2.4x
(8)
將式(8)計算值代入式(7),內摩擦角φ取37°,用Matlab計算屈服函數F在笛卡爾坐標系里等值線如圖2(b)所示,可以看出,屈服函數等值線最大F值出現在巷道的深部,說明煤巖由深至淺破壞,煤巖淺部完整,最終巷道側壁外緣完整塊體突然剝離。
內摩擦角φ取值分別為40°、45°、50°,C值由式(8)確定,其屈服函數等值線如圖2(c)~(e)所示。由圖2(c)~(e)可知,隨著內摩擦角φ的增加,其屈服函數等值線逐漸向深部移動,屈服函數等值線最大F值也在增大,這也印證了沖擊地壓多發生在硬巖或是硬煤巷道的規律。同時,由式(7)可知,圍巖的內摩擦角φ值越大,沖擊地壓發生的位置越深、能量釋放越強,造成的內部損傷也越嚴重;圍巖的黏聚力C值越大,破裂面越靠近深部。
2 屈服等值線的實驗驗證
為驗證屈服等值線的意義,運用有限元數值模擬軟件模擬塑性區域的分布,并通過室內實驗觀察塑性變形帶的形成。
2.1 端部約束壓縮實驗
實驗設備選用重慶大學MTS815.03 電動液壓伺服巖石實驗系統,煤樣取自天安煤礦(屬沖擊地壓礦井),被加工成?50 mm的標準圓柱型試樣,以0.2 mm/min恒定速率加載。在試樣端部采用卡箍固定,以模擬頂底板位移約束。煤樣破壞過程如圖3所示。

圖3 煤樣破壞過程
由圖3可知,在加載過程中煤樣破壞呈現階段性特征:①彈性階段煤樣應力呈線性緩慢增長,在約達到其抗壓強度的60%時,有少量的煤彈射出來,如圖3(b)所示;②隨著應力增大煤體繼續變形,當應力達到抗壓強度的78%左右時,煤體再次沖出,煤量較大,并伴隨著明顯的響聲,如圖3(c)所示;③隨后煤體逐漸由內向外鼓出,但沖擊現象并不明顯;④當應力達到峰值強度時,煤體中心部分出現斜剪裂紋,其破裂面基本呈現出雙曲線形狀,如圖3(d)所示。圖3(d)與圖2(a)所示情況非常相近。
2.2 煤體破壞趨勢數值分析
采用COMSOL Multiphysics 4.4平臺進行數值模擬,選用莫爾-庫侖屈服準則和Prandtl-Reuss增量方程,驗證內應力數值不均衡的情況。
計算區域內塑性應變分布如圖4所示(紅色區域表示塑性應變大,藍色區域表示塑性應變小)。

(a)矩形材料模型

(b)巷道模型
以煤體為矩形材料模型(煤體端部受到約束,豎直應力在矩形的中心較大,周邊稍小)的塑性應變分布結果如圖4(a)所示,模型大小為1.0×1.0。由圖4(a)可發現明顯的雙曲線形態的塑性區域分布,且在矩形尖部有較大的塑性變形累計,并逐步將煤體以三角形塊體整體形式切離。
上覆20 MPa壓力下巷道開挖后塑性變形情況如圖4(b)所示,模擬巷道尺寸為1.0×1.0。由圖4(b)可知巷道的兩幫有類似的雙曲線塑性變形分布,與應力分析得到的圖2(b)屈服函數等值線吻合。
3 現場觀測驗證
在沖擊地壓發生前,巷道會出現逐漸增大的鼓脹現象(如底鼓或幫鼓),直至發生突然失穩[16-17]。在巷道側壁,豎直應力逐漸由均勻荷載變為內大外小的狀態;在水平方向上,圍巖逐漸向巷道空間膨脹,但受到端部約束的影響越來越大,當形成如圖2(b)所示工況時,圍巖深部將形成一條貫通內外的屈服等值線。因此,可通過對巷道圍巖鼓脹量的判斷來表征約束應力的發展情況,也可以此判斷深部屈服等值線的發展情況;反之,通過對最大彈性鼓脹量計算也可以表征巷道沖擊地壓發生的臨界狀態。
一些典型沖擊礦井發生沖擊地壓后的現場情況如圖5所示。

圖5 典型沖擊礦井發生沖擊地壓后現場照片
由圖5可知,沖擊地壓發生后,巷道煤壁一側呈現出內凹的表面形狀和沖出巖體的三角形巖塊,與理論分析和試驗模擬結果相吻合。
4 結論
1)通過巷道力學模型模擬得到的應力狀態和雙曲線形式的屈服等值線,若屈服等值線數值由外至內逐漸增大,則表明圍巖深部破裂會導致煤巖體發生沖擊。
2)圍巖的內摩擦角越大,沖擊地壓發生的位置越深、能量釋放將越強;圍巖的黏聚力越大,破裂面越靠近深部。
3)室內單軸壓縮實驗表明,煤體破壞具有階段性特征,且由外到內逐層破壞,最終破裂面基本呈現雙曲線形狀。
4)當豎直應力由外向里逐漸增大時,煤巖體內部容易形成明顯的塑性變形帶,從而誘發沖擊地壓。

