城市公交線路運行可靠度分析及優(yōu)化
王夢琪 蒙素蘭 程鉛 杜文凱 林淦
(河海大學(xué)土木與交通學(xué)院,江蘇南京 210098)
1 研究背景
隨著城市交通的發(fā)展,大力發(fā)展公共交通已成為共識。公交在運營過程中由于受到天氣狀況、道路狀況等眾多因素的影響,運行可靠度較差,具體表現(xiàn)為各站點到達或發(fā)車不準(zhǔn)時、串車現(xiàn)象嚴(yán)重等問題。因此,需要從公交站點是否發(fā)生串車現(xiàn)象的角度考慮,判斷公交路線運行可靠性高低,并借此優(yōu)化公交運行。針對公交運行可靠性的研究,Avishai從可靠性的內(nèi)涵出發(fā),將公交服務(wù)可靠性定義為在一段時間內(nèi)提供穩(wěn)定服務(wù)的能力[1]。Tumnquist等提出公交服務(wù)可靠性是遵守時刻表或者保持規(guī)律的到站間隔的概率[2]。魏華構(gòu)建了公交服務(wù)水平評價體系,并將可靠性定義為:公交系統(tǒng)在道路動態(tài)交通條件下,能夠完成載客任務(wù)、給乘客提供一定水平服務(wù)的能力[3]。宋曉梅等借鑒可靠性理論定義了公交運行可靠性,從定性的角度分析了影響公共交通運行可靠性的因素,并針對這些因素提出了相應(yīng)的改善策略[4]。針對公交運行可靠性的研究,評價指標(biāo)的選取、可靠性評價等方面還不完善,需要進一步深入研究。故本文通過分析公交站點的串車現(xiàn)象評價公交線路運行穩(wěn)定性并進行優(yōu)化。
2 公交線路運行可靠性分析及優(yōu)化模型建立
2.1 時段劃分
由于道路交通的潮汐現(xiàn)象,公共線路行程時間會有時段變化特征,為避免或減弱這種現(xiàn)象的影響,本文將公交一天的運行時間劃分為幾個時段,如表1所示。

表1 時段劃分結(jié)果表
2.2 評價指標(biāo)選取
對于公交站點,串車現(xiàn)象是最直接反映公交站點可靠性的指標(biāo),而公交站點的可靠性又能進一步反映該公交線路運行可靠性高低,故選取判斷串車現(xiàn)象發(fā)生頻率的指標(biāo)對公交運行可靠性進行分析。
根據(jù)《公共交通通行能力和質(zhì)量服務(wù)手冊》中對串車現(xiàn)象的描述——當(dāng)實時的車頭時距大于計劃車頭時距的1/2時,即可判斷為串車現(xiàn)象。故選取車頭時距變異系數(shù)Cov(h)對公交站點串車現(xiàn)象進行分析。
2.3 公交運行數(shù)據(jù)集搭建
通過公交實際運行數(shù)據(jù)對三個不同時段分別搭建數(shù)據(jù)集,包括每相鄰兩輛公交車到達各站點的車頭時距及其平均值和標(biāo)準(zhǔn)差。
2.4 構(gòu)建公交串車現(xiàn)象判斷模型
2.4.1 計算公式
車頭時距變異系數(shù)Cov(h)的計算公式如式(1)所示:

其中,Cov(h)為車頭時距變異系數(shù);Sh為車頭時距的標(biāo)準(zhǔn)差;Dh為車頭時距的平均值。
2.4.2 判斷標(biāo)準(zhǔn)
判斷公交站點是否發(fā)生串車現(xiàn)象的標(biāo)準(zhǔn)為,Cov(h)的值為0.00~0.21表示公交到達站點的車頭時距與規(guī)定值非常一致,為0.22~0.30表示公交到達站點的車頭時距稍偏離規(guī)定值,為0.31~0.39表示公交到達站點的車頭時距經(jīng)常偏離規(guī)定值,為0.40~0.52表示公交到達站點的車頭時距波動大,部分車輛串車,為0.53~0.74表示公交到達站點會經(jīng)常性串車,不小于0.75表示該站點絕大部分的車輛處于串車狀態(tài)。數(shù)據(jù)來源:Transit Capacity and Quality of Service Manual-3rd Edition.
2.5 判斷公交站點是否發(fā)生串車現(xiàn)象
2.5.1 指標(biāo)計算
根據(jù)數(shù)據(jù)集中的數(shù)據(jù)通過式(1)計算不同時段內(nèi)不同發(fā)車時間間隔下各站點的車頭時距變異系數(shù)Cov(h)。
2.5.2 串車現(xiàn)象判斷
通過計算出的車頭時距變異系數(shù)Cov(h)的數(shù)值,判斷在不同發(fā)車時間間隔下公交站點是否發(fā)生串車現(xiàn)象以及發(fā)生串車現(xiàn)象的頻率。
2.5.3 優(yōu)化方法
若該時段內(nèi)在所有發(fā)車時間間隔下各公交站點發(fā)生串車現(xiàn)象的頻率較高,則選取發(fā)生串車現(xiàn)象最少的發(fā)車時間間隔作為該時段最佳發(fā)車時間間隔,將該時段內(nèi)公交發(fā)車時間間隔統(tǒng)一為該最佳發(fā)車時間間隔。
若該時段內(nèi)在所有發(fā)車時間間隔下各公交站點發(fā)生串車現(xiàn)象的頻率都很低,則說明該時段內(nèi)該公交路線的公交運行可靠性高,無需進行優(yōu)化。
2.6 驗證優(yōu)化方法
若對某時段內(nèi)的公交發(fā)車時間間隔進行調(diào)整,以此來優(yōu)化該公交路線的運行可靠性,則需要再次通過式(1)對該線路上各公交站點的車頭時距變異系數(shù)Cov(h)進行計算,并進一步判斷各公交站點發(fā)生串車現(xiàn)象的頻率,以此判斷通過調(diào)整發(fā)車時間間隔的優(yōu)化方法是否有效。
3 實例驗證
3.1 公交線路選取
選取南京市3號公交路線(往山西路方向)進行研究,該線路起始站以及終點站均為隨家倉,為環(huán)形公交線路。
3.2 數(shù)據(jù)選擇及指標(biāo)計算
通過對選取線路進行實地公交運行數(shù)據(jù)調(diào)查,選取早高峰這一時段的數(shù)據(jù)集進行分析。
選取早高峰公交運行數(shù)據(jù)集G1中發(fā)車時間間隔分別為5 min,4 min的數(shù)據(jù),計算對應(yīng)的各站點的車頭時距的平均值、標(biāo)準(zhǔn)差和車頭時距變異系數(shù)Cov(h),分別見表2,表3。
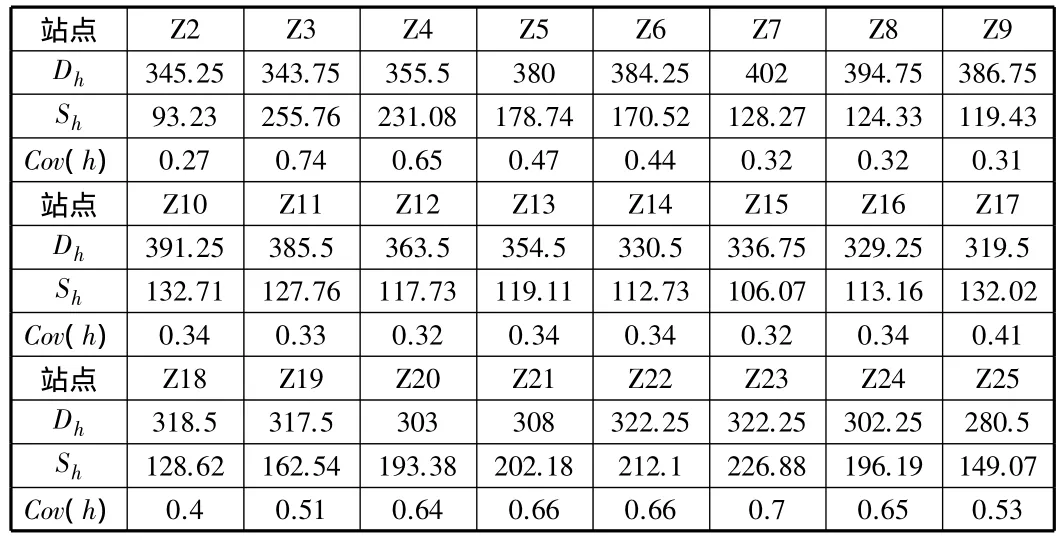
表2 發(fā)車間隔5 min數(shù)據(jù)計算表

表3 發(fā)車間隔4 min數(shù)據(jù)計算表
表中Z2表示該公交路線上的第2個公交站點,起始站為第1站。
3.3 串車現(xiàn)象分析及優(yōu)化
根據(jù)表2可以看出,早高峰該公交路線發(fā)車時間間隔為5 min時,該公交線路上大部分站點的車頭時距變異系數(shù)Cov(h)的值在0.31~0.39之間,根據(jù)評價標(biāo)準(zhǔn),說明公交車在該站點的車頭時距經(jīng)常偏離規(guī)定值。還有一大部分站點的車頭時距變異系數(shù)Cov(h)的值在0.53~0.74之間,說明該站點會有經(jīng)常性的串車現(xiàn)象。故可以判斷該公交線路上大部分站點會經(jīng)常產(chǎn)生串車現(xiàn)象,說明該公交線路公交運行可靠性低,需進行優(yōu)化。
據(jù)表3可以看出,早高峰該公交路線發(fā)車時間間隔為4 min時,該公交線路上大部分站點的車頭時距變異系數(shù)Cov(h)的值在 0.00~0.21 之間,部分在 0.22~0.30 之間,根據(jù)評價標(biāo)準(zhǔn),說明公交車在該站點的車頭時距與規(guī)定值基本一致,有時會稍微偏離規(guī)定值,進一步說明早高峰時段內(nèi)發(fā)車時間間隔為4 min時該公交路線的公交運行可靠性高。
根據(jù)兩個發(fā)車時間間隔下該路線公交運行可靠性的高低比較,可知在早高峰時,若將所有公交車輛的發(fā)車時間間隔均調(diào)為4 min,會減少公交站點串車現(xiàn)象的發(fā)生,提高公交運行可靠性。
4 結(jié)論
本文通過對一天中劃分的各個不同時段內(nèi)公交線路上各公交站點發(fā)生串車現(xiàn)象的頻率進行分析,判斷某時段內(nèi)公交路線運行可靠性高低,在此基礎(chǔ)上,對可靠性低的時段進行發(fā)車時間間隔調(diào)整,不斷調(diào)整發(fā)車時間間隔,直至找到使公交線路運行可靠性最高的發(fā)車時間間隔。該模型及優(yōu)化方法有效地降低了公交站點發(fā)生串車現(xiàn)象的頻率,提高了公交線路運行可靠性,對減緩交通流擁堵問題具有一定現(xiàn)實意義。

