粒子群優化灰色模型在沉降預測中的研究

陳家騏，司大雄，丁 蕾，丁碧瑩

(合肥學院 建筑工程系，合肥 230601)

基坑工程不僅要保證基坑本身的安全與穩定，更要有效控制基坑周邊地層位移以保護周邊設施的安全[1]。如今基坑的開挖深度越來越大，工程的地質條件越來越差，基坑距離周圍建筑物或者市政設施越來越近，基坑工程事故不斷發生。預測基坑工程周邊地表沉降是基坑工程安全施工及周邊既有建筑沉降安全評估的基礎，準確有效地對基坑周邊地表沉降預測和鄰近建筑安全隱患的預警對安全文明施工有著重要的意義。鄧聚龍于1982年提出灰色系統理論后，經過多年發展，已充分運用在各種安全預測領域[2-5]。其中DGM(1,1)模型的參數估計、數據擬合及預測均采用離散方程，不存在離散模型與連續模型之間的近似替代，具有較高的預測精度。但由于施工期間外界因素的擾動，沉降監測數據并不能完全反應真實的沉降規律，此外由于模型本身建模時迭代初始值使用缺陷，導致最終的預測結果與真實結果存在一定偏差。利用變權緩沖算子對原始數據進行新序列構造，可以有效地緩解外界因素的不良擾動，并運用粒子群算法對緩沖算子可變權重及新序列初始值的缺陷進行優化，快速搜尋到全局最優解，建立優化模型，提高預測精度。工程實例計算表明，二維粒子群優化DGM(1,1)模型能有效提高預測性能。

1 灰色預測模型

1.1 DGM(1,1)模型

定義1[6]：設序列X(0)=(x(0)(1),x(0)(2),…,x(0)(n))，其中x(0)(k)≥0,k=1,2,…,n.則稱X(1)=(x(1)(1),x(1)(2),…,x(1)(n))為序列X(0)的一次累加生成序列，其中

(1)

定義2[7]：設序列X(0),X(1)如定義1所述，則稱

x(1)(k+1)=β1x(1)(k)+β2

(2)

為離散灰色預測模型DGM(1,1)模型，或稱為GM(1,1)模型的離散形式，其中β1，β2為估計參數。

定理1[7]：設X(0)為非負原始序列，

X(0)=(x(0)(1),x(0)(2),…,x(0)(n))

(3)

其一次累加1-AGO序列為

其中

X(1)=(x(1)(1),x(1)(2),…,x(1)(n))

(4)

(5)

對式(2)使用最小二乘法，則離散灰色預測模型的估計參數β1，β2滿足

β=(β1，β2)T=(BTB)-1BTY

(6)

其中

定理2[7]：設B,Y,β如定理1所述，β=(β1，β2)T=(BTB)-1BT，取x(1)(1)=x(0)(1),則離散灰色預測模型的解為:

(7)

其中k=1,2,…,n-1

還原值為:

k=1,2,…,n-1

(8)

1.2 變權弱化緩沖算子

定理3[8]：設X=(x(1),x(2),…,x(n))為非負的系統行為數據序列，令

XD1=(x(1)d1,x(2)d1,…,x(n)d1)

(9)

其中，

x(k)d1=λx(n)+(1-λ)x(k)

(10)

其中，λ為可變權重，0<λ<1;K=1,2,…,n，當X為單調增長序列、單調遞減序列或震蕩序列時，稱D1為變權弱化緩沖算子。

1.3 迭代初始值

且

(11)

1.4 精度檢驗

1)平均相對誤差α

(12)

2)后驗差比C

C=S2/S1

(13)

S1為原始序列的標準差；S2為擬合序列與原始序列的殘差序列的標準差。

3)灰色絕對關聯度

(14)

(15)

(16)

2 粒子群算法優化模型

2.1 粒子群算法原理

假設在D維空間中有m個粒子，粒子i在D維空間的位置向量為xi=(xi1,xi2,…,xiD),粒子i在D維空間的速度向量為vi=(vi1,vi2,…,viD)。將粒子的空間位置向量帶入目標函數f(x)求得適應值，根據適應度最大或最小準則判斷該位置是否為最優位置，個體粒子i飛過的歷史最好位置為pi=(pi1,pi2,…,piD),群體中所有粒子飛過的最好位置為pg=(pg1,pg2,…,pgD)[9]。粒子群算法中的粒子速度和位置按如下公式進行更新：

速度更新公式：

viD(t+1)=ω×viD(t)+c1×r1×(piD(t)-xiD(t))+c2×r2×(pgD(t)-xiD(t))

(17)

位置更新公式：

xiD(t+1)=xiD(t)+viD(t+1)

(18)

其中i=1,2,…,m

式中：t為迭代次數；viD為第i個粒子在第D維空間的速度；xiD為第i個粒子在第D維空間的位置；piD(t)代表第i個粒子在第D維中迭代t次時最好的位置pgD(t)代表粒子種群在第D維空間中迭代t次時最好位置；ω為慣性權重；c1是自我學習因子；c2是群體學習因子；r1,r2是[0 1]區間內的隨機數。

2.2 粒子群算法的建模過程及參數設置

針對DGM(1,1)模型的不足，先后將式(10)與式(11)帶入DGM(1,1)模型中構造優化DGM(1,1)模型，優化模型中的可變權重λ與修正系數β3作為待優化參數建立二維空間粒子群算法模型，以平均相對誤差最小為準則，對緩沖算子的可變權重以及緩沖算子構造后新數據序列迭代初始值進行優化。

建模過程如下：

1)初始化設置。慣性權重ω取0.8；學習因子c1,c2在0到4之間，本算法模型取c1=c2=1.5;迭代次數t取值過大或過小會導致計算變慢或計算精度不足，本算法模型迭代次數選取t=100；優化DGM(1,1)模型中待優化參數λ與β3作為二維空間種群中的個體粒子，初始種群粒子個數取i=100；初始粒子的速度vi及位置xi用隨機數函數給出。

2)適應度值計算。利用式(12)平均相對誤差作為目標適應度函數分別計算適應度值。

3)個體極值與全局最優解。隨機生成初始粒子λ與β3帶入優化DGM(1,1)模型進行適應度值計算，采用式(17)和(18)更新粒子速度和位置。個體極值為每個粒子找到的歷史上最優位置信息pbest，并從個體歷史最優解中找到全局最優解gbest，并與歷史最優解比較，選出最佳的粒子λ與β3作為當前的歷史最優解。

4)循環迭代計算。以式(12)全局最小為準則，判斷目標適應度值是否滿足要求，如不滿足要求則繼續迭代計算直至滿足最優準則或最大迭代次數。

5)計算結束。計算結束后得到優化DGM(1,1)模型最優參數參數λ與β3。

6)最終預測模型建立。使用求得的最優參數λ與β3構造優化DGM(1,1)模型，并利用該模型進行預測。

3 模型驗證及工程應用

3.1 工程概況

地鐵雞鳴山路站車站為合肥市軌道交通4號線工程的第1個車站，車站有效站臺中心里程為K1+280.000。車站主體為地下兩層兩跨島式站臺車站，結構形式為地下兩層兩跨/三跨/四跨矩形框架結構。車站主體采用明挖法施工，附屬結構采用明挖法施工。圍護結構采用鉆孔樁+內支撐的支護體系。

3.2 分析預測

選取該工程周邊地表沉降觀測點DB2-1的等時距12期觀測數據作為模型檢測數據組。其中前10期數據作為原始序列利用章節2.2的方法建立二維粒子群優化DGM(1,1)預測模型，并對第11、12期數據進行預測，后2期數據作為檢驗數據與預測值比對，評估優化模型的預測性能。

利用表2中前10期數據分別帶入傳統DGM(1,1)模型和待優化的DGM(1,1)預測模型中。傳統模型利用原始數據直接建模，待優化模型利用粒子群算法求得優化參數λ=0.0248，β3=-0.03512，利用優化參數構造二維粒子群優化DGM(1,1)模型。上述兩種模型的模擬結果比對如表3所示。精度檢驗見表4。

表2 測點DB2-1沉降觀測數據

為了更加直觀的看出傳統模型和優化模型擬合預測性能的差別，將擬合結果及相對誤差繪制如圖1、2、3所示。

圖1 模型擬合結果比對圖

從圖1中可看出，由傳統DGM(1,1)模型所擬合的曲線相比于原始數據曲線，總體走勢誤差較大，第3、4、6、10期數據的偏差在圖中可以明顯看出。這由于傳統DGM(1,1)模型中未考慮迭代初始值對模型本身的影響。由二維粒子群優化DGM(1,1)模型所擬合預測的曲線相比傳統模型，因為考慮迭代初始值的作用，第3、4、6、10期數據的偏差相比傳統模型顯著減小，且作為檢驗數據的第11、12期數據，偏差均小于傳統模型。

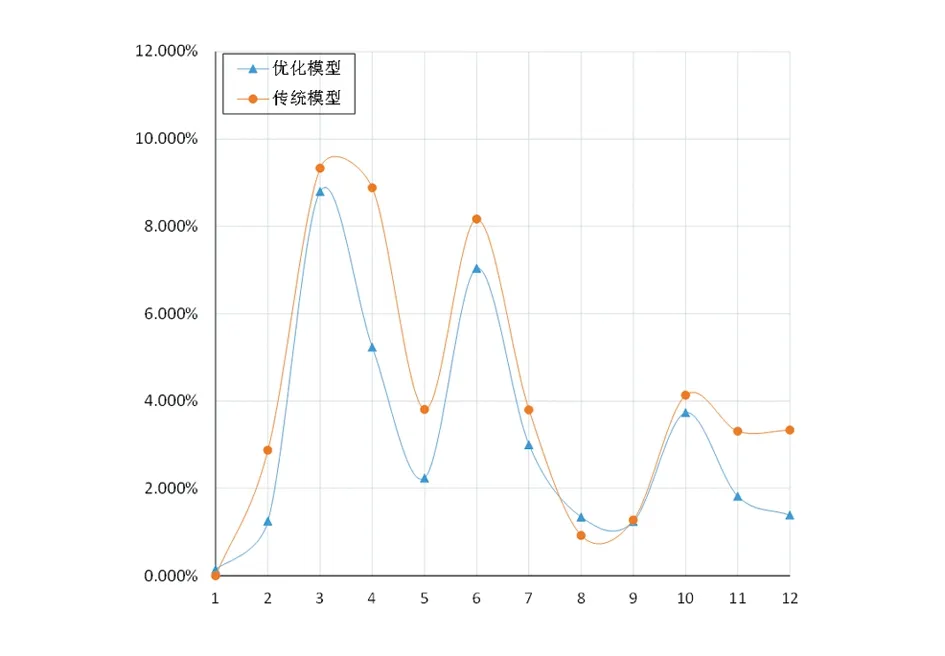
圖2 模型擬合相對誤差對比圖

圖3 模型擬合殘差對比圖

從圖2和圖3可看出，由優化模型所以擬合的曲線整體相對誤差及殘差波動小于傳統模型，且由優化模型所預測的第11、12期數據的相對誤差遠小于傳統模型。

由表3的擬合及預測數據可以看出，優化DGM(1,1)模型各期數據的殘差及相對誤差大部分小于傳統DGM(1,1)模型。優化模型及傳統模型在第3、4、5、6期的擬合數據出現較大的相對誤差，原因是在這幾期監測時段，監測數據受到外界不可控因素的擾動而失真，導致整個監測數據不能反映真實變化規律，出現擬合偏差。但優化模型受到緩沖算子的數據還原作用，使得預測第11、12期監測數據時，其預測值的相對誤差只有1.82%和1.39%，殘差絕對值為0.06和0.05，而傳統模型第11、12期預測值的相對誤差為3.31%和3.34%，殘差絕對值為0.109和0.120。優化模型的殘差絕對值遠小于傳統模型，而優化模型預測值的平均精度相比傳統模型提高了約52%。

由表4的精度檢驗結果可知，傳統DGM(1,1)模型和二維粒子群優化DGM(1,1)模型均有良好預測精度，其預測精度均為一級。優化模型的相對誤差3.39%，相比于傳統模型的4.53%，其預測精度提高了30%。優化模型的后驗差比為0.12，相對于傳統模型的0.17，預測性能提高42%。優化模型的灰色絕對關聯度高于傳統模型，說明利用優化模型擬合預測結果具有更好的有效性。

綜上所述，傳統DGM(1,1)模型與二維粒子群優化DGM(1,1)模型均具有良好的預測精度。但優化模型相比于傳統模型，由于運用粒子群算法優化彌補了迭代初始值的缺陷，并用緩沖算子弱化外界因素對數據真實性的干擾，具有更高的預測可靠性及更好的模擬效果。

表3 模型擬合預測值

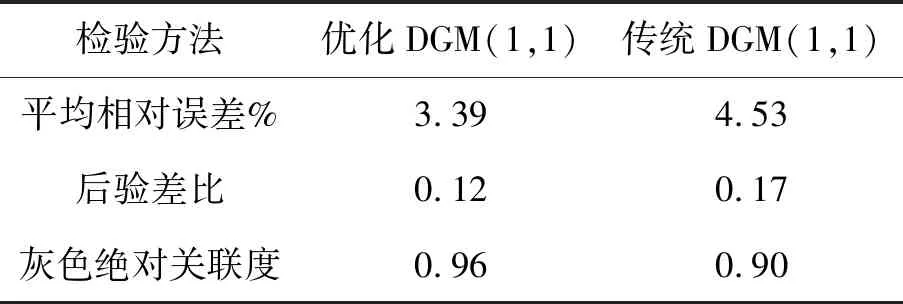
表4 模型精度檢驗

4 結論

運用粒子群算法對緩沖算子可變權重以及新序列初始值進行二維優化，進而提高了DGM(1,1)模型預測性能。將優化模型應用于基坑周邊地表沉降預測領域，并得出以下3點結論：

(1)運用粒子群算法全局搜索快的特點對模型本身建模時迭代初始值缺陷進行彌補優化，解決最終的預測結果與真實結果存在偏差的問題。

(2) 運用變權緩沖算子對原始數據進行新序列構造，有效的緩解外界因素的不良擾動，并用粒子群算法搜尋最優權重。

(3)二維粒子群優化DGM(1,1)模型簡單，易于施工人員掌握及運用，能準確有效的對基坑周邊地表沉降進行預測，并為鄰近既有建筑安全隱患的預警預報提供依據。