層次分析法在A*中的運用

聶宸菡

（北京建筑大學 測繪與城市空間信息學院,北京100044）

當發生油氣管道發生事故時，將不可避免地會對社會、環境等造成損害。建立應急救援系統是減少造成損害的有效方法，其中緊迫性是最顯著的特征。當救援物資要求以最短時間到達事故現場時，決策者必須選擇最佳路徑，因此有人提出了啟發式搜索算法: A*算法[1]。層次分析法（AHP）是由Saaty 開發的一種多標準決策（MCDM）技術，用于復雜的決策問題。 它采用多層次的層次結構，最終目標和實現這一目標的替代方案。AHP 不僅可以幫助決策者制定正確的決策，而且可以幫助他們找到最適合他們需求的解決方案以及他們對問題的理解[2]。在本文中，我們使用AHP 方法分析和比較影響最佳路線選擇的四個阻抗因子，并給出每個因子的權重（優先級）。 然后，我們為研究區域的道路網絡中的每個路段分配了權重值，通過使用該權重值而不是經典算法的距離權重值來改變經典A*算法。

1 A*算法

A*算法屬于一種最經典的啟發式搜索算法之一，是建立在Dijkstra 和BFS 算法基礎上的，也屬于遍歷搜索算法，但因為采用了啟發式方法來估計地圖上任意點到目標點的代價, 從而可以智能地評估每個相關節點，只按照最可能最正確的方向去搜索，而忽略其他不相關的節點或者背離目標節點的方向。A*算法引入了當前節點n 的啟發函數f(n),當前節點n 的啟發函數定義為:

其中g(n)是從起點到當前節點n 的實際費用的量度,h(n)是從當前節點n 到終點的最小費用的估計。

經典的A*算法中f 函數的構造為距離權重為主，而在實際尋找最佳路徑中，大多數使用距離作為權重來解決最佳路徑問題，在緊急情況下選出最佳路徑，必須考慮其他因素。分析這些元素所占比重，將用到層次分析法，下節將介紹層次分析法的步驟。

2 層次分析法

2.1 建立層次結構模型

首先，構建層次結構模型。模型中有三個級別：

（1）最高級別是引發的問題，稱為目標級別。

（2）中間層是來自分解的復雜問題的元素，稱為準則級別。

（3）最低級別是問題的度量和方案，稱為方案級別。

在本文中，通過調查實時交通狀況來選擇阻抗因素。在我們的方法中，我們選擇了影響最佳路徑選擇的四個阻抗因子：道路質量、交通流量、交通狀況、天氣。

2.2 成對比較

在層次分析法過程中，在確定各層次各因素之間的權重時，如果只是定性的結果，則常常不容易被別人接受，因此兩兩相互比較，對此時采用相對尺度，以盡可能減少性質不同的諸因素相互比較的困難，以提高準確度。（如表1 所示）。

表1 元素之間的相對重要性

2.3 建立比較矩陣

在進行兩兩比較后，輸出的為一個比較矩陣，它包含了每對因素的比率，比較矩陣是nxn 矩陣，n 為因素數量。比較矩陣A為：

為了更接近實際狀況，在上述所建立的比較矩陣中，每個元素采用三角模糊數構造的比較矩陣A 和道路數據調查分析出最小值和最大值取值，因此最終模糊比較矩陣Af為：

2.4 歸一化、計算權重

通過使用幾何平均方法對前一步驟的比較矩陣進行歸一化來計算每個因素的總權重。如下等式：

其中aij是比較矩陣Af的元素值。

在計算歸一化的比較矩陣之后，可以如下等式所示計算總權重向量。

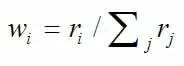
2.5 一致性檢驗

層次分析法的最后一步是計算成對比較矩陣的檢驗系數。檢驗系數（C.R.）是根據人為判斷和感知衡量比較矩陣的一致性。如果C.R.＜0.1 ，則認為該比較矩陣通過一致性檢驗，否則就不具有滿意一致性。檢驗系數可以計算為：

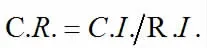
λ 為比矩陣的最大特征值，用最大特征值對應的特征向量作為被比較因素對上層某因素影響程度的權向量。CI 越大，不一致越嚴重。由此可得比較矩陣最大特征值λ=4.0263，C.I.=0.0088，C.R.=0.0097。根據結果，當C.R. ＜0.10 時，比較矩陣的一致性是可以接受的，否則應該修改比較矩陣。所以Af是可以接受的，對應于A 的最大特征值的單位特征向量為：

因此得出影響程度的大小順序為：交通狀況、交通流量、道路質量和天氣狀況。

2.6 權重的運用

在通過一致性檢驗后，計算出阻抗因素權重向量，將使用此權重向量計算出每條路線的總權重，把總權重代替經典A*算法中權重因子[4]。但由于各個阻抗因素的測量單位不一致，因此需要對阻抗因素進行歸一化。為了更接近實際情況，每個阻抗因素需根據實際情況采用不同的方式進行歸一化，如天氣因素所占比重低，說明在進行歸一化時需最小化來選擇最佳路徑。交通狀況因素所占比重高，說明在進行歸一化時需最大化來選擇最佳路徑。對于那些需要最大化的因素，歸一化公式如下：

最小化所采取的的歸一化公式：

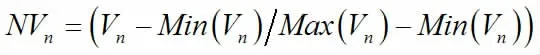
最終道路權重為：

3 實驗與分析

本文利用改進的A*算法對交通網絡圖進行加權搜索。測試的地圖，包括周邊城市區域，來自于地理信息系統。搜索結果如下所示：

表2 結果對比

我們改進了經典的A*算法，將其權重因子替換為層次分析法法中的總權重因子。此外，我們還對改進后的算法進行了測試，并與經典的A*算法進行了比較。結果表明，該方法比經典的A*算法更有效。