四維超混沌Chen 系統的有限時間同步

周子渝 侯 晨 周有嶒 馮 瑜*

（玉林師范學院 數學與統計學院，廣西 玉林537000）

隨著科學技術飛速發展，人們的信息保密工作變得越來越重要.而如今，混沌加密是應用最廣泛的通訊保密技術。由于正的Lyapunov 指數會使吸引子運行軌跡會變得互不相關，而它們的軌道將很快變得互不相關，以致混沌系統對初始條件具有很高的敏感依賴性，即完全相同系統對于極小差異的初始條件，其運行軌跡存在著很大不同，這使混沌加密成為信息安全領域研究一大熱點[1]。

自1990 年，Pecora L M 和Carroll T L 提出了混沌同步的方法，首次采用驅動- 響應系統實現了兩個系統的同步[2]，使混沌系統應用到信息保密通信領域成為可能. 早期應用的混沌系統是低維的，其安全性并不高，由于密鑰空間不夠，易受到外來明文的攻擊，其密鑰也容易被破譯。隨著研究的深入，越來越多的研究學者發現低維混沌系統存在著不安全性與局限性，開始轉向對超混沌系統進行研究. 超混沌系統因其密鑰空間的復雜性，在很大程度上提高了通訊保密工作的安全性，為信息安全領域提供了豐富的信息源。如[3]-[4]探討了不同種類的超混沌系統的有限時間同步問題。

只有混沌信號達到同步狀態才能正確解密，從而得到正確的明文信息。迄今已提出了各種實現混沌信號同步方法，如驅動- 響應同步法、投影同步法及自適應同步法等[5]。本文主要運用驅動- 響應同步法，利用合理的控制器，對四維超混沌Chen系統進行定性分析研究，使兩個超混沌系統達到同步狀態。

1 基本定義

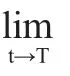
定義2：設x˙=f（x）+g（x）u 為控制系統，其中u 為控制函數，V（x）為正定函數且是該系統的一個控制Lyapunov 函數，若函數V（x）是無窮可微的，則由LgV（x）=0（x≠0）可得到LfV（x）＜0。[3]

2 確定參數系統的有限時間同步

基 于Lyapunov 函 數 穩 定 定 律，取 參 數（a，b，c，d）=（35，3，12，7，0.2）時，系統處于超混沌狀態。其中x1，x2，x3，x4為系統的狀態變量，a，b，c，d，r 為系統實參數。

四維超混沌Chen 系統[6]：

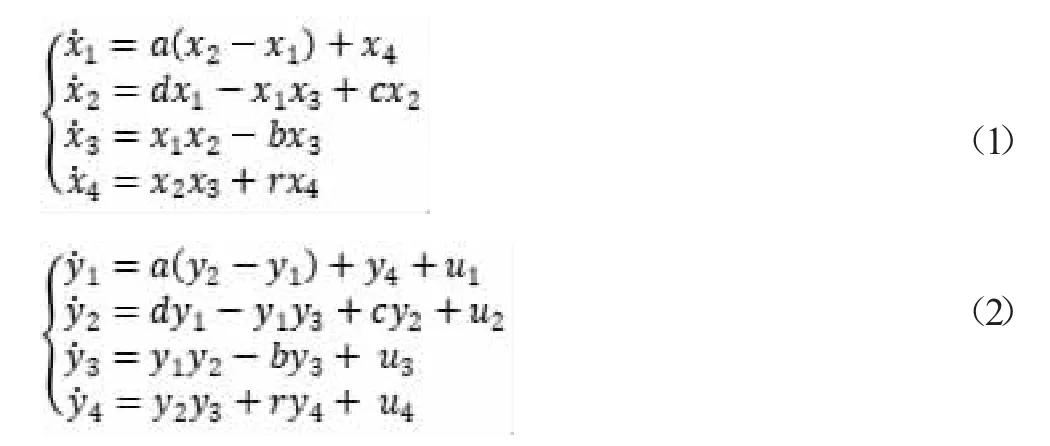
其中（1）式為驅動系統，（2）式為響應系統，為使（1）式與（2）式達到同步狀態，在（2）式中每個方程右邊都加上系統同步控制變量ui（i=1，2，3，4），令ei=yi-xi（i=1，2，3，4）為（1）式和（2）式之間的狀態誤差。

則誤差方程為：

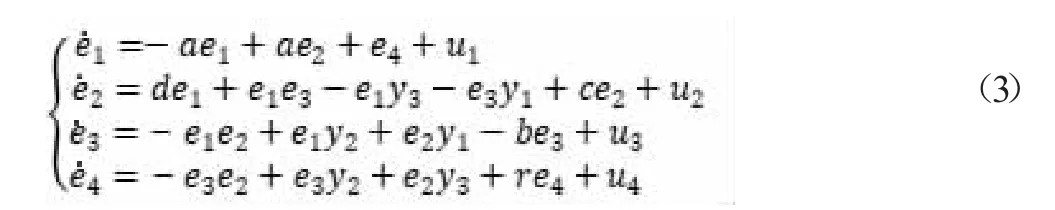
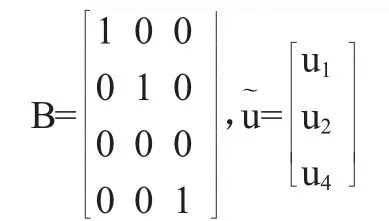
證明 由題設知。

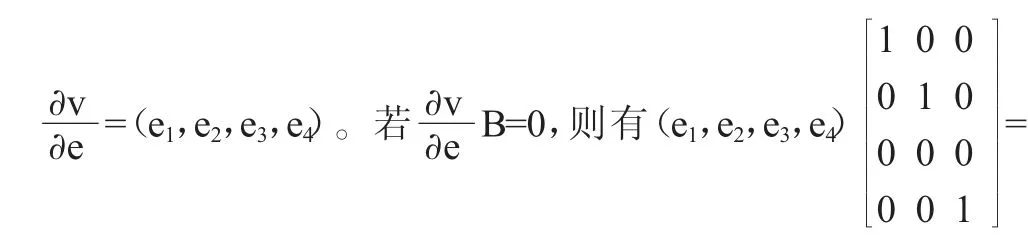
（e1，e2，e4），即e1=e2=e4=0，從而

所以V（e）是系統（4）的控制Lyapunov 函數。

引理2 選取控制器為[6]

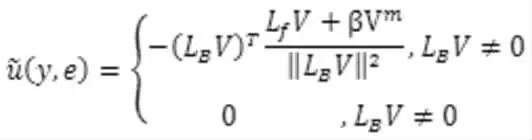
時，在有限時間T 內使得（1）式與（2）式達到同步狀態。

3 仿真研究

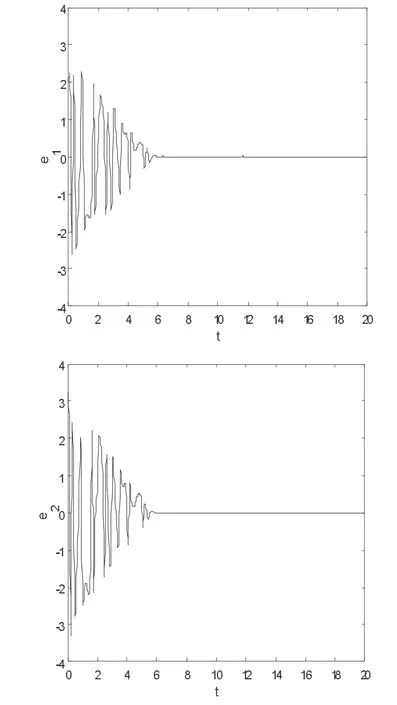
本文考慮響應系統在控制器作用下與驅動系統的同步仿真，在有限時間同步仿真研究中，選取系統參數值（a，b，c，d）=（35，3，12，7，0.2），驅動系統及響應系統所取初始值分別為（x1，x2，x3，x4）=（2-4 3-1），（y1，y2，y3，y4）=（4-1 2-3）時間步長t=0.0002s，再利用MATLAB 軟件進行數值仿真，我們發現驅動系統（1）將在時間T=6s 內與響應系統（2）達到同步，確定參數系統仿真結果如圖所示。分析得出，仿真結果與理論分析結果一致。