僅考慮自重的細長受彎構件是否需滿足長細比要求的研究

謝琴，范曉南（四川建筑職業技術學院 四川 德陽 618000）

0 引言

在鋼筋混凝土結構或鋼結構中，受壓構件并不少見。建筑結構中常見的受壓構件包括柱、剪力墻、基礎等等。受壓構件包括軸壓構件、壓彎構件和壓彎扭構件等等。對于長細比較小的受壓構件，通常發生的是強度破壞，因此其截面尺寸由強度或經驗公式控制；而長細比較大的受壓構件容易發生屈曲失穩現象，因此其截面尺寸除了需滿足強度條件外，還需考慮長細比的限制[1]。《鋼結構設計標準》中規定，為保證受壓構件的穩定性，受壓構件長細比不得超過150。結構構件若發生屈曲失穩現象，將對整個結構的穩定性造成極其嚴重的影響。因此，應盡量避免結構構件發生屈曲失穩現象。在實際工程中，有些細長構件主要承受橫向荷載，豎向荷載可僅考慮自重，如路燈桿，旗桿，鐵架等。這些桿件豎向荷載僅為沿桿軸均勻分布的自重，橫向荷載主要為風荷載。討論在這類構件的設計中，除了滿足橫向荷載以及豎向荷載的承載能力外，是否還需考慮規范中對長細比的限制。

1 受壓構件的屈曲

《鋼結構設計標準》中規定，軸心受壓柱、桁架和天窗架中的壓桿，容許長細比為150，但當桿件的內力設計值不大于承載能力的50%時，容許長細比值可取200。規范中限制受壓構件的長細比是為了防止構件發生失穩現象，即屈曲。構件失穩時，其截面應力并不一定很大，有時甚至低于比例極限。當桿件受到的壓力達到某一值時，桿件可達到微小彎曲平衡狀態，該壓力值即為桿件失穩的臨界壓力值[2]。當桿件受到的壓力值小于臨界壓力值時，這時如果壓力撤銷，桿件能恢復直線狀態，此時桿件處于穩定平衡狀態；當桿件受到的壓力值大于臨界壓力值時，此時桿件會發生不可逆的持續大變形，即屈曲，壓力撤銷后，桿件不能恢復原始直線狀態。由此可見，受壓桿件不發生屈曲失穩的條件為桿件所受壓力值小于失穩臨界壓力值[4]。由桿件保持微小彎曲平衡狀態的撓曲線微分方程可得臨界壓力值計算公式，即歐拉公式：

式中，Fcr 為桿件失穩臨界壓力值，E 為材料的彈性模量，I 為截面最小慣性矩，μ 為桿件長度因數，可查表得到，l 為桿件長度。

2 僅考慮自重的受彎構件失穩計算

對若干長度和截面尺寸不同的僅考慮自重的受彎構件進行計算，通過比較構件所受軸壓力及失穩臨界壓力值的大小，判斷構件僅在自重作用下是否會發生屈曲現象。所列舉的桿件均為懸臂桿件，其支座約束條件為一端固定端，另一端自由端。僅列舉長度為9.3m，截面尺寸為Φ300×12 且僅考慮自重的受彎構件的軸壓力及失穩臨界壓力值的具體計算過程，其余桿件僅列出最終計算結果。

長度為9.3m，截面尺寸為Φ300×12 的桿件自重計算過程如下。

其中，W 為桿件自重，γ 為桿件的容重，鋼材的容重可取平均值γ=7 850kg/m3，V 為桿件的體積。

該桿件的失穩臨界壓力值計算過程如下。

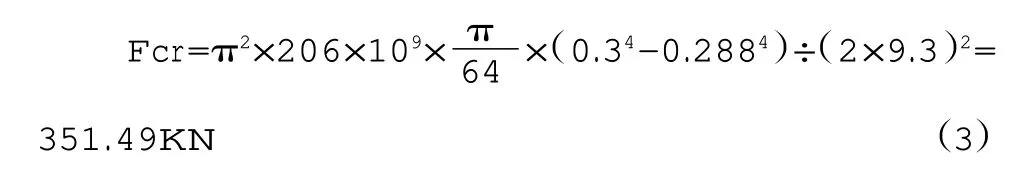
其中，鋼材彈性模量為206Gpa，一端固定端，另一端自由端的桿件的長度因數μ 為2。

由上述計算可見，在僅考慮自重的情況下，受橫向荷載作用的桿件的自重遠小于失穩臨界壓力值，即W≤Fcr°由桿件失穩的本質可得，此時桿件不會發生屈曲失穩現象。需要說明的是，桿件的自重是沿桿長均勻分布的，但討論桿件是否失穩時，為計算方便，取自重的合力，并將該合力作用在自由端，這種簡化的受力狀態相較于桿件實際的受力狀態對于探討失穩問題來說更為不利，因此得到的結果是偏安全的。

按照上述計算過程計算了若干工程中常見的不同長度及截面尺寸的桿件的自重及失穩臨界壓力值，探討上述結論是否具有普遍性。具體計算過程省略，僅列出部分計算結果，如表1：

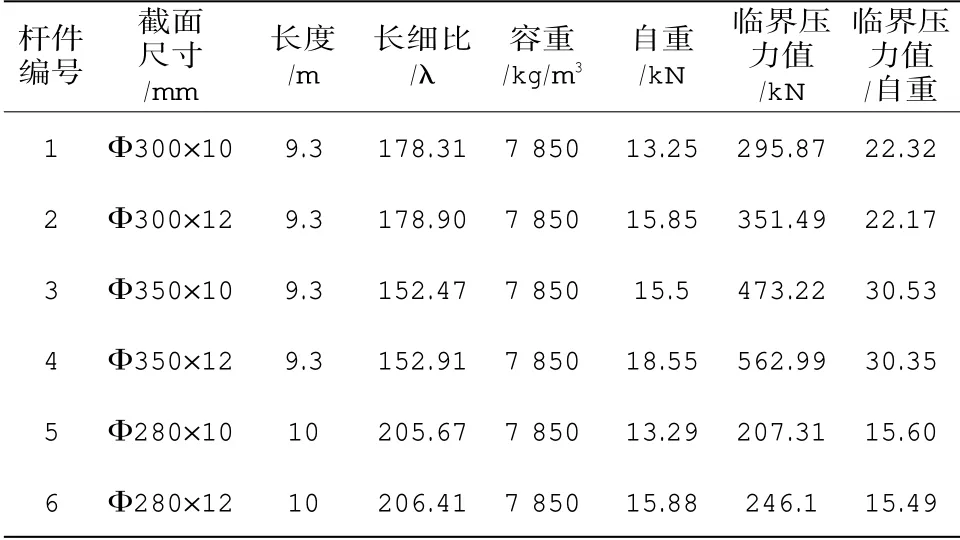
表1 桿件自重及臨界壓力值

通過表1 可以看出，不同截面尺寸及長度的桿件，通過計算得到的自重均遠小于失穩臨界壓力值。具體變化規律如下：

（1）不同截面尺寸、不同長度的桿件計算所得長細比λ 大部分都在150 以上，大于規范規定值；

（2） 不同截面尺寸、不同長度的桿件的臨界壓力值均遠大于自重，說明僅考慮自重且承受橫向荷載的桿件在自重作用下不至于屈曲失穩；

（3） 長細比λ 越大，臨界壓力值與自重的比值越小，說明桿件長細比的增大，對桿件保持穩定性來說是一個不利因素。綜上所述，僅在自重作用下的受彎桿件雖然長細比超出規范規定值，但其臨界壓力值均遠大于自重，因此不可能發生屈曲失穩現象。

3 桿件失穩的條件

雖然工程中常見的僅考慮自重且承受橫向荷載的桿件由于臨界壓力值遠大于自重，但如果桿件長細比太大，桿件仍有發生屈曲失穩現象的可能。因此，討論長細比很大且僅在自重作用下的受彎桿件不發生屈曲失穩現象的條件很有必要。

由桿件自重公式及失穩臨界壓力公式可推導得桿件不發生屈曲失穩的條件。

僅考慮自重的受彎桿件不發生失穩現象需滿足：

對于薄壁鋼管，其體積V=π×（R2-r2）×l，截面慣性矩因此可得：

其中，D 為桿件外部直徑，d 為桿件內部直徑，R 為桿件外部半徑，r 為桿件內部半徑。

公式（6）即為桿件不發生屈曲失穩現象需滿足的條件。工程中常見的僅考慮自重的受彎桿件大部分均能滿足公式（6）。

4 結語

通過分析比較工程中常見的僅考慮自重的細長受彎構件的自重和失穩臨界壓力值，得如下結論：

（1） 工程中常見的僅考慮自重的受彎構件的自重均遠小于失穩臨界壓力，因此，在設計時可不考慮《鋼結構設計標準》中關于受壓構件長細比限值的規定，直接認為這類構件不會發生屈曲失穩的現象；

（2） 通過對比不同截面尺寸及長度的構件的自重及失穩臨界壓力值的比值可知，雖然工程中常見的這類構件不會發生屈曲失穩現象，但當長細比λ 越大時，失穩臨界壓力值與自重的比值越小，因此長細比λ 的增大對桿件保持穩定性是一個不利因素；

（3） 通過桿件自重及失穩臨界壓力值的公式推導，可得僅考慮自重的受彎桿件不發生屈曲失穩的條件為工程中大部分僅考慮自重的受彎構件均能滿足此條件。