基于動力剛度矩陣的波形鋼腹板PC連續箱梁橋自振頻率分析

羅 奎，冀 偉，張經偉

(蘭州交通大學 土木工程學院，甘肅 蘭州 730070)

0 引言

波形鋼腹板PC組合箱梁橋是一種鋼-混凝土組合結構橋梁。用波折狀的鋼腹板來替代傳統的混凝土腹板，使混凝土和鋼材各自的優點得到充分的發揮，即波形鋼腹板主要承擔剪力，而混凝土板主要承擔拉、壓力，同時也使結構變得輕型化且避免腹板開裂，從而降低成本、便于維修、提高預應力的施加效率和橋梁的耐久性[1]。

國內外諸多學者已經在波形鋼腹板PC箱梁橋的靜力和動力問題方面開展了大量的理論和試驗研究。在靜力問題的分析和計算方面，Nguyen等[2]研究了不等端彎矩作用及不同約束條件下的波形鋼腹板 Ι 型鋼梁的彎矩修正系數；Yi等[3]、Eldib[4]和Hassanein等[5]研究了波形鋼腹板的剪切屈服強度；Moon等[6-7]研究了波形鋼腹板 Ι 型鋼梁的屈曲性能和波形鋼腹板的抗剪強度；聶建國等[8]引入波形鋼腹板剪切變形轉角位移函數，建立了考慮腹板剪切行為的波形鋼腹板理論模型，將波形鋼腹板的彎曲行為分解為桁架作用和彎曲作用，給出了波形鋼腹板簡支梁端部無約束和有約束在均布荷載和跨中集中荷載作用下的解析解，隨后根據變形等效原理，引入影響參數,對波形鋼腹板梁變形的解析解做了進一步簡化，給出了鋼腹板剪切變形的簡化計算方法——有效剛度法[9]；劉保東等[10]同時考慮波形鋼腹板PC箱梁的剪力滯效應和鋼腹板的剪切變形效應，推導出了該橋型的撓度計算公式。國內學者對波形鋼腹板PC箱梁橋的動力特性也做了大量的研究。任紅偉等[11]推導了波形鋼腹板梁橋扭轉振動頻率的計算公式；張永健等[12]制作了波形鋼腹板混凝土試驗梁，并對其動力特性進行了測試；李波等[13]給出了波形鋼腹板PC箱梁橋的等效阻尼比的求解方法，可為此橋型動力特性計算中阻尼的取值提供參考依據；冀偉等[14-17]考慮箱梁的剪力滯效應、波形鋼腹板的剪切變形效應及兩者的耦合效應，對波形鋼腹板PC箱梁橋的動力特性做了大量的理論和試驗研究。

雖然國內外對波形鋼腹板PC箱梁橋動力特性的研究已取得了顯著的成就，但目前對波形鋼腹板PC箱梁橋動力特性的矩陣分析方法的研究成果較少。大多數學者推導的理論解析解只適用于特定的邊界條件和荷載，此外采用ANSYS有限元建立實體模型進行分析費時費力。因此，本研究運用能量變分原理，以波形鋼腹板PC箱梁截面的豎向位移、彎曲角位移及剪切角位移為未知節點位移函數，推導出波形鋼腹板PC箱梁橋考慮鋼腹板剪切變形的單元剛度矩陣。據此，采用MATLAB軟件編制考慮鋼腹板剪切效應影響下波形鋼腹板PC箱梁橋自振頻率計算的求解程序。所編寫程序的計算結果得到了實測值和三維有限元值的驗證。可將考慮鋼腹板剪切變形效應下該橋型的動力分析問題簡便地納入普通桿系結構矩陣位移體系中，避免了ANSYS有限元模型建立和求解的復雜性，可為該橋型的自振頻率的計算和分析提供一定的參考依據。

1 波形鋼腹板的外形尺寸與有效剪切模量

波形鋼腹板的外形構造及尺寸如圖1所示。

圖1 波形鋼腹板的尺寸

Samantn等[18]指出鋼腹板的剪切模量與外形尺寸有關，并給出鋼腹板有效剪切模量Gs的求解公式：

(1)

式中，α=(D1+D2)/(D1+D3)；D1，D2，D3分別為波形鋼腹板斜板段在水平面的投影長度、平板段長度和斜板段的長度(如圖1所示)；H為波形鋼腹板的波高；Es和νs分別為鋼材的彈性模量和泊松比。

2 波形鋼腹板PC箱梁橋的單元剛度矩陣和單元質量矩陣

2.1 基本假定

(1)由于混凝土頂、底板與波形鋼腹板在彈性范圍內協同工作，不考慮波形鋼腹板和與混凝土頂、底板之間的相對滑移。

(2)不考慮波形鋼腹板PC箱梁的剪力滯效應和扭轉變形。

(3)由于波形鋼腹板的空間效應(即手風琴效應)，忽略其抗彎能力。

在豎向荷載作用下，波形鋼腹板PC箱梁橋的波形鋼腹板產生較大的剪切變形，使得混凝土頂、底板在初等梁理論的基礎上再產生一個轉角η，如圖2所示。ω,ξ,η分別為波形鋼腹板PC箱梁截面的豎向位移、彎曲轉角位移和剪切轉角位移，3者均是關于x的函數。

圖2 波形鋼腹板PC箱梁在豎向荷載作用下的變形

取該橋型橫截面的一半進行分析，如圖3所示。bs和bx分別為混凝土頂、底板的寬度的一半；ts，tx和tw分別為混凝土頂、底板和波形鋼腹板的厚度；h1和h2分別為混凝土頂板下邊緣和混凝土底板上邊緣到波形鋼腹板PC箱梁整體截面形心軸的距離；hs和hx分別為混凝土頂、底板形心軸到波形鋼腹板PC箱梁整體截面形心軸的距離。

圖3 波形鋼腹板PC箱梁的截面尺寸

混凝土頂、底板和波形鋼腹板的縱向位移如式(2)～式(5)所示:

us(x,z)=hsξ(x)-(z+hs)η(x)，

(2)

uw(x,z)=[hs-κ(z+h1)]ξ(x)-

(3)

ux(x,z)=-hxξ(x)-(z-hx)η(x)，

(4)

ω=ω(x)，

(5)

2.2 波形鋼腹板PC箱梁單元剛度矩陣的推導

由基本假設，波形鋼腹板PC箱梁的混凝土頂、底板和波形鋼腹板的應變如式(6)～式(10)。

混凝土頂板的正應變：

εs=hsξ′(x)-(z+hs)η′(x);

(6)

混凝土頂板的切應變：

γs=ω′(x)-η(x);

(7)

波形鋼腹板切應變：

γw=ω′(x)-κξ(x)+χη(x);

(8)

混凝土底板的正應變：

εx=-hxξ′(x)-(z-hx)η′(x);

(9)

混凝土底板的切應變：

γx=ω′(x)-η(x)。

(10)

上述式中,εs和εx分別為波形鋼腹板PC箱梁混凝土頂、底板的正應變；γs,γx,γw分別為波形鋼腹板PC箱梁混凝土頂板、底板和波形鋼腹板的切應變；ξ′(x),η′(x)和ω′(x)分別為ξ(x),η(x),ω(x)對x求一階導數。

波形鋼腹板PC箱梁的應變能和外力勢能如式(11)～式(14)。

混凝土頂板的應變能：

(11)

波形鋼腹板的應變能：

(12)

混凝土底板的應變能：

(13)

外力勢能：

(14)

人類賴以生存的地球只有一個，其土地極其有限，且不復繁殖。所有人都受惠于土地：生者藉之以生產、生活，死者除少數天葬、海葬，大多則是“入土為安”，筑墓立碑，供眷屬、族人憑吊。生者繁衍不息，死者延綿不斷，人類似乎越來越感受到土地“供不應求”的窘況。

(15)

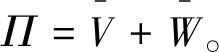
(16)

由式(6)～式(16)得到波形鋼腹板PC箱梁的總勢能。

q0(ξ′)2-2q0ξ′η′+q1(η′)2+

q0(η′)2-qω]dx，

(17)

波形鋼腹板PC箱梁的梁單元節點位移如圖4所示。

圖4 梁單元的節點位移

圖4中，ωi和ωj分別為梁單元i,j兩端的豎向位移；ξi和ξj分別為在初等梁理論條件下梁單元i,j兩端產生的轉角；ηi和ηj分別為由于波形鋼腹板的剪切變形使梁單元i,j兩端產生的轉角。采用滿足精度要求的形函數N(x)進行插值，則ω(x)，ξ(x)，η(x)可表示為：

(18)

(19)

(20)

波形鋼腹板PC箱梁的單元剛度方程可表示為：

Keδe=Fe，

(21)

式中，Ke為單元剛度矩陣；δe和Fe分別為單元節點位移矢量和節點力矢量。

將形函數取為線性函數，即：

(22)

由式(17)～式(20)和式(22)求得波形鋼腹板PC箱梁的總勢能П。

Π=Π(ω,ξ,η)。

(23)

根據高等數學知識，波形鋼腹板PC箱梁的總勢能П取駐值時需要滿足：

(24)

將(24)的結果整理成矩陣的形式如式(25)所示：

(25)

結合式(21)和式(25)可得波形鋼腹板PC箱梁的單元剛度矩陣Ke為：

(26)

(27)

(28)

式中，A11=A12=A13=A14=A15=A16=A21=A24=A31=A34=A35=A41=A42=A43=A44=A45=A46=A51=A53=A54=A61=A64=0;A22=A26=A62=A55=-A23=-A32=-A25=-A52=-A56=-A65=q0;A33=A66=-A36=-A63=(q0+q1)。

式中，B11=B44=-B14=-B41=6(p0+p1)；B12=B21=B15=B51=-B45=-B54=-B24=-B42=3κp0l;B13=B31=B16=B61=-B34=-B43=-B46=-B64=-3(χp0-p1)l;B22=B55=2κ2p0l2;B25=B52=κ2p0l2;B23=B32=B56=B65=-2χκp0l2;B26=B62=B35=B53=-χκp0l2;B33=B36=B63=2(χ2p0+p1)l2;B66=(χ2p0+p1)l2。

2.3 波形鋼腹板PC箱梁單元質量矩陣的推導

根據文獻[19]，波形鋼腹板PC箱梁的單元質量矩陣M可以按式(30)計算：

(30)

式中，ρ為材料密度；A為波形鋼腹板PC箱梁的橫截面積；l為梁單元的長度。

根據波形鋼腹板PC箱梁的單元剛度矩陣Ke和單元質量矩陣M，采用MATLAB有限元軟件編寫了波形鋼腹板PC箱梁橋的自振頻率計算的求解程序，限于篇幅具體程序不再贅述。

3 算例分析

算例選取2005年在河南省建造的某座等截面波形鋼腹板PC連續箱梁橋。該橋全長120 m，采用 4×30 m等跨布置，施工方法為先簡支后連續，由4片主梁構成，單片主梁的截面尺寸如圖5所示。

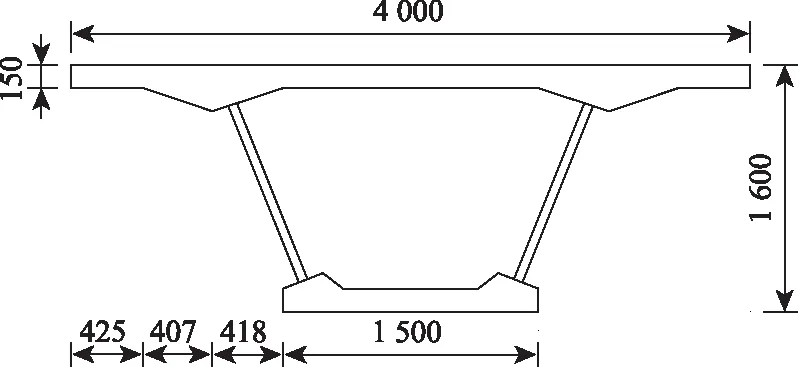
圖5 單片梁的截面尺寸(單位：mm)

大橋的混凝土頂板、底板及橫隔板的混凝土材料均為C50，混凝土的彈性模量為Ec=3.5×1010Pa，泊松比為vc=0.166 7，混凝土的密度為ρc=2.5×103kg/m3。波形鋼腹板的鋼材為Q355C級低合金結構鋼，厚度為8 mm，鋼材的彈性模量為Es=2.1×105MPa，泊松比為vs=0.30，鋼材的密度ρs=7.8×103kg/m3。波形鋼腹板的波高取值為150 mm, 波形鋼腹板斜板段在水平方向的投影長度為200 mm，平板段長度為250 mm，斜板段長度為250 mm。

采用ANSYS 18.0有限元軟件建立了大橋的三維有限元模型。橫隔板和混凝土頂板、底板采用SOLID 45實體單元進行模擬，波形鋼腹板采用SHELL 63殼單元進行模擬，建立的大橋三維有限元模型如圖6所示。

圖6 大橋的ANSYS模型

采用本研究方法計算了大橋前5階彎曲振動頻率，將其結果與大橋彎曲振動頻率實測值[20]及ANSYS空間有限元值進行了比較，如表1所示。

表1 大橋彎曲振動頻率對比

注：②差比=|(②-①)/①|；③差比=|(③-①)/①|。

從表1中可以看出，根據本研究所推導的波形鋼腹板PC箱梁橋的單元剛度矩陣，采用MATLAB軟件編制的求解程序計算所得的自振頻率值與實測值和ANSYS三維有限元值吻合較好，驗證了本研究在考慮波形鋼腹板剪切效應下所推導的波形鋼腹板PC箱梁的單元剛度矩陣的正確性，同時也驗證了采用MATLAB軟件所編制自振頻率求解程序的適用性。

4 參數分析

4.1 波折形狀對彎曲振動頻率的影響

假定大橋的梁截面的細部尺寸和計算跨徑保持不變，用本研究編寫的MATLAB程序分別計算了大橋在不同波形鋼腹板形狀下的彎曲振動頻率。目前國內外采用的波折形狀主要有4種：1000型、1200型、1600型和2400型，如圖7所示。4種標準形狀波形鋼腹板剪切模量的修正系數如表2所示，大橋的前5階彎曲振動頻率如表3所示。

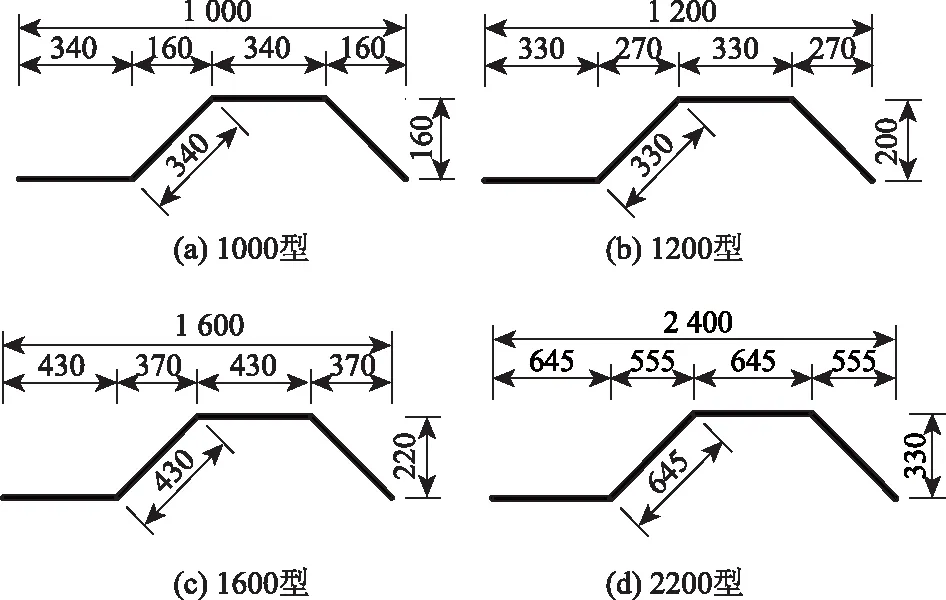
圖7 標準形狀的波形鋼腹板(單位：mm)

從表3可以看出，采用不同的波形鋼腹板型號所計算的大橋前5階彎曲振動頻率的差值在0.55%以內，說明波形鋼腹板的形狀對其彎曲振動頻率的影響較小，可以將其忽略不計。

表2 標準形狀的波形鋼腹板的修正系數

表3 大橋在不同波折形狀下的彎曲振動頻率對比

4.2 波形鋼腹板剪切模量的修正對彎曲振動頻率的影響

采用本研究方法分別計算了考慮和不考慮修正波形鋼腹板剪切模量兩種情況下大橋的彎曲振動頻率值，如表4所示。可以看出，不考慮修正剪切模量計算所得的大橋前5階自振頻率值比考慮修正剪切模量的情況要略微偏大，前5階彎曲振動頻率的差值不超過1.07%。因此，在計算其彎曲振動頻率時將其忽略不計。

4.3 波形鋼腹板剪切變形對彎曲振動頻率的影響

采用本研究編寫的MATLAB程序分別對是否考慮波形鋼腹板的剪切變形效應對大橋的彎曲振動頻率進行求解，結果如表5所示。經對比分析可知，不考慮剪切變形計算所得大橋的前5階彎曲振動頻率值比考慮其剪切變形效應的計算值要大，兩者的差值隨著彎曲振動頻率階數的升高而增大，第5階彎曲振動頻率值兩者差值已達到15.52%。因此，波形鋼腹板剪切變形效應對波形鋼腹板PC連續箱梁橋的彎曲振動頻率的影響不可忽略。

表4 剪切模量是否修正所得大橋彎曲振動頻率值比較

注：差比=(②-①)/②。

表5 是否考慮剪切變形所得大橋彎曲振動頻率對比

注：差比=(②-①)/②。

4.4 基頻與現行規范進行對比

我國2015年發布的《公路橋涵設計通用規范》(JTG D60—2015)第4.3.2條給出的連續梁橋豎向基頻的估算公式為[21]：

(31)

(32)

式中，l為橋梁的計算跨徑；E為橋梁材料的彈性模量；Ic為橋梁跨中位置的截面慣性矩；mc為橋梁跨中位置單位長度的質量。

根據規范規定，計算連續梁橋的沖擊力所引起的正彎矩效應和剪力效應時，采用基頻f11；計算連續梁橋的沖擊力引起的負彎矩效應時，采用基頻f12。采用《公路橋涵設計通用規范》中的式(31)和式(32)對大橋的豎向基頻進行了計算，并將其結構與本研究方法所得基頻進行比較，結果如表6所示。

從表6中可以看出，采用本研究程序計算的豎向基頻與《公路橋涵設計通用規范》所給公式計算值相差很大，兩者的差值達到了37.73%和139.26%。因此，《公路橋涵設計通用規范》中給出的連續梁的豎向基頻的估算公式不再適用于波形鋼腹板PC連續箱梁橋的豎向基頻的計算。

表6 大橋豎向基頻的計算值與規范對比

注：②差比=(②-①)/①；③差比=(③-①)/①。

5 結論

(1)考慮波形鋼腹板剪切效應推導了波形鋼腹板PC箱梁橋的單元剛度矩陣，利用MATLAB軟件根據其單元剛度矩陣編制了等截面波形鋼腹板PC連續箱梁橋的自振頻率求解程序。本研究方法可靠性得到了已建實橋彎曲振動頻率實測值和ANSYS空間有限元值的驗證。

(2)波形鋼腹板的剪切模量是否修正以及波形鋼腹板的型號對波形鋼腹板PC連續箱梁橋彎曲振動頻率的影響較小，且前5階彎曲振動頻率的差值在1.07%～0.55%以內。因此，在求解等截面波形鋼腹板PC連續箱梁橋自振頻率時可以不考慮波形鋼腹板剪切模量的修正系數以及波形鋼腹板型號。

(3)波形鋼腹板PC連續箱梁橋自振頻率的計算計入波形鋼腹板剪切變形的影響，采用本研究的方法對自振頻率的計算結果與文獻[20]實測值和ANSYS三維有限元值吻合較好。

(4)考慮波形鋼腹板剪切變形，本研究采用MATLAB軟件編制的波形鋼腹板PC連續箱梁橋自振頻率計算的求解程序具有較高的精度，可指導設計和施工。

(5)研究成果可將考慮剪切變形效應下波形鋼腹板PC連續梁橋的動力分析問題，方便地納入普通桿系結構矩陣位移體系中，避免了ANSYS有限元模型建立和求解的復雜性。