隔震曲線連續梁橋粘滯阻尼器參數優化分析

王浩， 沈惠軍， 張寒， 鄭文智， 沙奔， 李愛

(東南大學 混凝土及預應力混凝土結構教育部重點實驗室，江蘇 南京 210096)

曲線梁橋因其外形美觀、適應性強的特點，而被廣泛應用于各類山區公路和城市道路的橋梁工程。由于其平面不規則，地震作用下的受力更為復雜[1]。當采用隔震體系時，為了滿足其位移需求，邊墩處通常采用四氟滑板橡膠支座，但已有研究表明，地震作用下，由于邊墩四氟滑板橡膠支座可發生相對滑移，上部結構的地震作用將主要由中墩來承擔，從而會導致邊墩、中墩受力不均衡。針對此問題，目前通常采用隔震支座加阻尼器的組合方法對結構的地震響應進行控制。粘滯阻尼器的力-位移滯回曲線非常飽滿，耗能限位能力強，能在不增加地震慣性力的情況下，有效地控制橋梁結構的位移響應[2-3]。此外，粘滯阻尼器還具有構造簡單、便于施工、受激勵頻率和溫度影響小的特點，因此很受工程技術人員的青睞，成為減小橋梁結構關鍵部位地震響應的主要手段之一[4-7]。

為了使粘滯阻尼器達到預期的效果，有必要對其參數進行優化分析。對此，國內外諸多學者開展了相關研究。文獻[8]通過建立與粘滯阻尼器參數相關的拉格朗日方程，利用順序搜索法求解阻尼器參數的最優解。文獻[9]為優化粘滯阻尼器對雙塔斜拉橋的減震效果，應用最小二乘回歸分析法建立關鍵截面參數與阻尼參數之間的數學模型，以控制截面內力和變形最小為原則，通過求解擬合方程的極值得到最優設計參數。文獻[10]針對現有阻尼器參數優化方法的缺陷，基于斜拉橋的隨機地震響應，通過最小化粘滯阻尼器的阻尼力得到阻尼器參數的最優解。以上關于粘滯阻尼器參數優化的研究對象均是斜拉和懸索等大跨度柔性橋梁，針對連續梁橋的相關研究還不夠系統，特別是對曲線連續梁橋則更為少見[11-12]。顯然，對隔震曲線連續梁橋采用粘滯阻尼器進行減震控制優化研究有待進一步加強。

為此，本文以某三跨隔震曲線連續梁橋為研究對象，采用非線性動力時程法，分析了粘滯阻尼器阻尼系數和速度指數對其地震響應的影響。在此基礎上，基于零階優化算法，以各墩墩底剪力之和為目標函數，進行了粘滯阻尼器參數優化分析，旨在為隔震曲線連續梁橋的減震設計與研究提供參考。

1 隔震曲線連續梁橋分析模型

該隔震曲線連續梁橋跨度為3×35 m，位于曲率半徑為200 m的平曲面上。主梁采用現澆預應力混凝土箱梁，其截面為單箱雙室，橋墩采用圓形雙柱墩，其具體尺寸分別見圖1(a)、(b)。中墩、邊墩處支座類型分別為鉛芯橡膠支座、四氟滑板橡膠支座。該隔震曲線連續梁橋構造圖如圖1所示，其中，橋墩編號為P1～P4，支座編號為B1～B4。由設計資料可知，該橋址區的抗震設防烈度為9度，場地類別為二類。

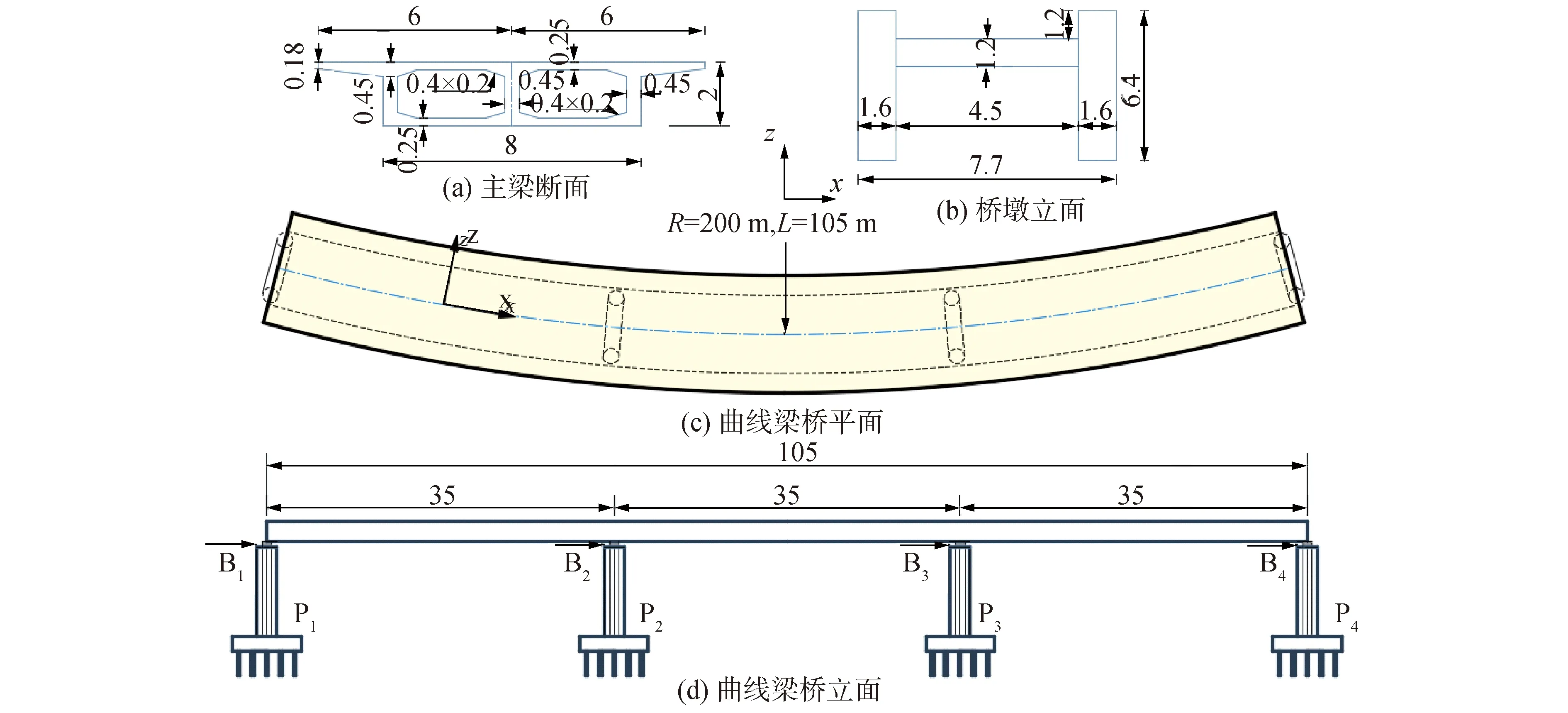
圖1 隔震曲線連續梁橋構造(單位: m)Fig.1 The structure of the isolated continuous curved girder bridge (unit: m)

基于ANSYS建立該橋的空間有限元模型，如圖2所示。主梁、橫梁和橋墩采用彈性梁單元模擬，中墩鉛芯橡膠支座、邊墩四氟滑板橡膠支座水平切向和徑向均采用COMBIN40單元模擬，豎向采用COMBIN14單元模擬。鉛芯橡膠支座和四氟滑板橡膠支座的力學模型分別如圖2(a)和(b)所示，其優化前的力學模型參數如表1所示。主梁和支座之間采用剛性單元連接，橋墩底部固接，未考慮樁土相互作用。

表1 隔震支座簡化力學模型參數Table 1 Simplified mechanical parameters of isolation bearings

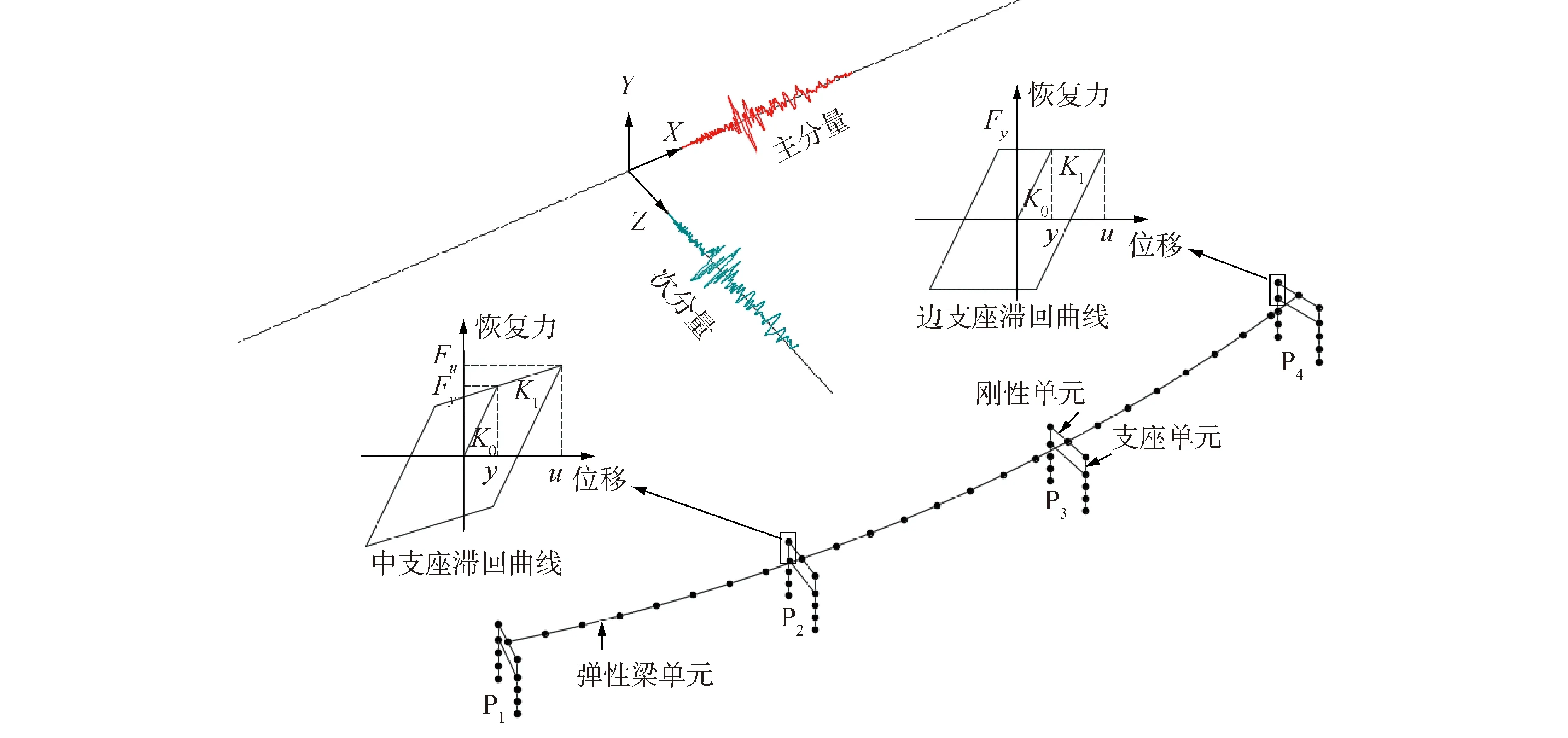
圖2 隔震曲線連續梁橋有限元模型Fig.2 Finite element model of the isolated continuous curved girder bridge

2 粘滯阻尼器參數敏感性分析

2.1 地震動輸入

根據場地剪切波速，從PEER地震動數據庫中選取了3條地震波，其信息如表2所示。根據《公路橋梁抗震設計細則》[13]，將地震動主、次分量的加速度峰值分別調整為0.4、0.34 g。本文僅研究了水平雙向地震動輸入的情況，未考慮豎向地震動的影響。

表2 地震加速度記錄Table 2 Acceleration records of the earthquake

2.2 參數敏感性分析

地震作用下，當該橋邊墩四氟滑板橡膠支座發生相對滑移時，該支座提供的恢復力不再增加，上部結構的地震作用將主要通過鉛芯橡膠支座傳遞給中墩來承擔，從而導致邊、中墩受力不均衡。因此，在兩邊墩處沿徑向和切向各設置一個粘滯阻尼器。以期增大結構阻尼，減小支座位移，同時有效調節結構內力在各墩之間的分配。下面以內側四氟滑板橡膠支座(B1)和內側橋墩(P1、P2)為研究對象，分析粘滯阻尼器參數對其地震響應的影響。其中，阻尼系數c取值范圍為0～3 MN·(m/s)-α，速度指數α分別取0.3、0.5、0.7、1.0。Northern Calif-03地震動作用下的計算結果如圖3、圖4所示。

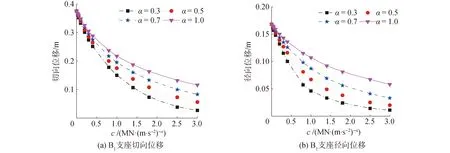
圖3 c和α對B1支座位移的影響Fig.3 The effect of c and α on the displacement of the B1 bearing

由圖3可知，當α一定時，支座切向和徑向位移隨著c的增大而減小，且逐漸趨于平緩，c取值在0～1 MN·(m/s)-α內，對支座切向和徑向位移的影響較為顯著；當c一定時，支座切向和徑向位移隨著α的減小而減小。當c和α分別取3 MN·(m/s)-α和0.3時，支座切向和徑向位移減幅均高達88.89%。由此說明，當c和α取值合理時，粘滯阻尼器可以對隔震曲線連續梁橋的位移響應進行較好的控制。由圖4可知，當α一定時，邊墩墩底切向和徑向剪力隨著c的增大而增大，而中墩的變化規律相反；當c一定時，α越小，對中、邊墩墩底切向和徑向剪力的影響越大。

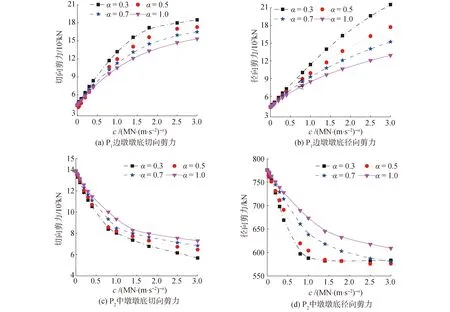
圖4 c和α對橋墩墩底剪力的影響Fig.4 The effect of c and α on the shear force at the bottom of piers

由此可知，存在一個最優的c和α，可以使得邊、中墩受力更為均衡，同時有效減小支座位移。以上粘滯阻尼器的參數敏感性分析提供了一個參數取值范圍，為了進一步得到最優參數的具體值，以下進行優化分析。

3 粘滯阻尼器參數優化

3.1 零階優化算法

零階優化算法是在一定次數的抽樣基礎上，擬合設計變量、狀態變量和目標函數的響應函數，從而尋求最優解，故又可稱其為子問題方法。函數曲線的形式可采用線性擬合、平方擬合或平方交叉項擬合。對于含設計變量和狀態變量的約束問題，可采用罰函數將其轉化為無約束的最小值問題[14]。

該方法是建立在目標函數及狀態變量近似的基礎上，若采用平方交叉項擬合，則目標函數的擬合公式為：

(1)

式中：xi、xj為設計變量；a0、ai、bij為擬合系數，擬合系數隨迭代過程而變，由加權最小二乘法確定。

利用罰函數將上述有約束問題的目標函數轉化為無約束問題的目標函數[15]，其擬合公式為：

(2)

式中：xi為設計變量；gi、hi、wi為狀態變量；X、G、H、W為對應的罰函數；f0為目標函數參考值；pk為響應面參數；無約束目標F(X,pk)為響應面函數，隨設計變量X及響應面參數pk而變化。

3.2 優化模型的建立

基于零階優化算法，對粘滯阻尼器參數進行優化分析。優化過程中，阻尼系數c和阻尼指數α為設計變量，其取值范圍為：

(3)

將支座位移作為含有約束條件的狀態變量，以各墩底切向剪力絕對值之和為目標函數fob：

(4)

式中：Fi為單墩墩底切向剪力；Ui-T為支座切向位移；Ui-R為支座徑向位移；ρ2為容差，其值為1×10-3。

3.3 優化結果分析

由于Northern Calif-03地震作用下的結構地震響應最大，基于上述優化模型，開展粘滯阻尼器參數優化分析。優化后的切向粘滯阻尼器參數c和α分別為0.775 MN·(m/s)-α、0.411；徑向粘滯阻尼器參數c和α分別為0.386 MN·(m/s)-α、0.633。

為了分析隔震曲線連續梁橋粘滯阻尼器優化后的減震效果，基于上述優化后的參數，采用非線性動力時程法，進行了有、無粘滯阻尼器時支座位移和墩底剪力的對比分析，其結果分別如表3、4所示，相應的支座位移和墩底剪力時程曲線如圖5、6所示。

表3 支座位移及其減震率Table 3 The displacement of bearings and its damping rate

注：T代表切向、R代表徑向。

表4 墩底剪力及其減震率Table 4 The shear force at the bottom of piers and its damping rate

注：T代表切向、R代表徑向。

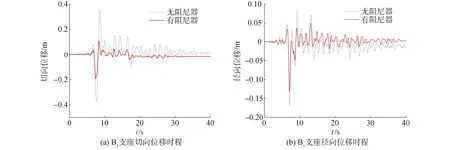
圖5 支座位移時程Fig.5 The displacement time history of the bearing

由表3和圖5可知，阻尼器優化后，支座切向和徑向位移減震率分別在47%和22.2%以上，切向位移和徑向位移分別在0.2 m和0.15 m以內。兩中墩支座和兩邊墩支座的位移減震率分別保持一致，而中墩支座與邊墩支座間的位移減震率相差較大。中墩支座的切向位移減震率高于邊墩支座，而邊墩支座的徑向位移減震率高于中墩支座。

由表4和圖6可知，阻尼器優化后，邊墩墩底切向剪力明顯增大，最大增加了139.1%，最小也達到了106.8%，中墩墩底切向剪力減震率在38.3%以上。邊墩墩底徑向剪力增大的幅度相對較小，但也在77.5%以上，而中墩墩底徑向剪力的減震率最大僅9.1%。值得注意的是，設置阻尼器后，雖然各墩墩底剪力之和僅變化了1.6%，但中墩與邊墩的墩底剪力差值大幅度減小，其中，切向剪力差值由956 kN減小為220 kN，徑向剪力差值由441 kN減小為130 kN，邊、中墩受力更為均衡。總體而言，在邊墩處設置粘滯阻尼器，對邊墩墩底剪力的影響大于中墩，對墩底切向剪力的影響大于徑向。

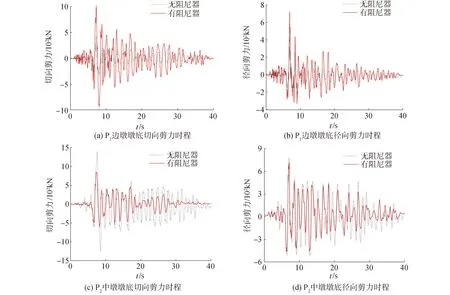
圖6 墩底剪力時程Fig.6 The shear time history at the bottom of piers

4 結論

1)合理的粘滯阻尼器參數可以使隔震曲線連續梁橋邊、中墩在地震作用下的受力更為均衡，同時有效控制橋梁位移。

2)采用優化后的粘滯阻尼器參數，支座位移減幅明顯，切向和徑向位移的減幅分別在47%和22.2%以上。中墩支座的切向位移減幅高于邊墩支座，而邊墩支座的徑向位移減幅高于中墩支座。

3)設置粘滯阻尼器前后的各墩墩底剪力之和基本無變化，但墩底剪力差值大幅度減小，邊、中墩受力更為均衡。