一種基于周期性特征的數據中心在線負載資源預測方法*
梁 毅,曾紹康,梁巖德,丁 毅
(北京工業大學信息學部,北京 100124)
1 引言
隨著大數據產業的發展,數據中心得到了較為廣泛的關注和較大的投入建設。負載是數據中心應用的運行實例,也是數據中心資源使用的主體。以Web服務、流式計算為代表的在線負載是其中一類長時運行、延遲敏感的負載。由于在線負載受到用戶行為驅動,負載強度具有較大的波動性,在運行過程中其資源需求動態變化。在線負載資源需求預測一直以來都是數據中心資源管理領域的研究熱點。快速、準確的在線負載資源需求預測是數據中心合理分配資源、保障負載執行效率的關鍵。
數據中心在線負載資源預測方法已得到廣泛關注和研究。總結而言,既有方法可分為3類:基于簡單統計分析方法、基于時間序列分析方法和基于機器學習方法。
簡單統計分析方法是指通過對資源使用數據采用統計分組、相關分析等方法分析在線負載資源使用情況,對當前在線負載資源需求進行預測[1,2]。然而,單純采用簡單統計分析的方式無法更準確地挖掘在線負載資源使用的特征和變化趨勢。
針對簡單統計分析方法的不足,時間序列分析方法被引入數據中心資源預測。既有工作主要采用AR(Auto Regressive model)分析法[3 - 5]、自相關和互相關方法[6,7]以及ARIMA(Auto Regressive Integrated Moving Average)方法[8 - 13]對數據中心單負載及混部負載場景下應用的CPU、內存、磁盤及網絡資源需求進行預測。然而,上述時間序列分析方法多適用于短期預測,難以對在線負載的長時運行的資源需求進行準確預測。
隨著機器學習的發展,相關算法被廣泛應用到了在線負載資源預測中。既有工作主要采用多元線性回歸方法[14 - 16]、聚類方法[17,18]、支持向量回歸方法[19 - 21]及馬爾科夫模型[22 - 25]進行應用資源使用預測。文獻[26]針對在線負載,測試了線性回歸、神經網絡和支持向量回歸等算法在CPU需求預測上的性能,發現在各算法中支持向量回歸算法的預測結果更準確且表現最優。然而,機器學習算法的預測準確度依賴于大規模樣本數據的訓練,而大規模數據的訓練會導致較大的時間開銷,無法滿足在線負載實時性的場景。
然而,上述研究成果尚存在2點不足:(1)既有基于簡單統計分析和時間序列分析的預測方法多著眼于短期預測,難以獲得較為準確的長期預測值;(2)既有基于機器學習的預測方法準確度依賴于大規模樣本數據,且具有較大的時間開銷,難以適應在線負載快速響應、延遲敏感的需求。
針對上述問題,本文將在線負載資源使用的周期性特征引入資源預測中,提出基于周期性特征的在線負載資源預測方法PRP(Periodical characteristic based Resource Prediction)。PRP通過資源使用變化周期識別和資源使用樣本子序列分類,將在線負載的長期資源預測轉化為短期預測,通過加權綜合不同類資源使用子序列獲得快速、準確的在線負載資源預測。本文的主要貢獻可歸納為3個部分:
(1)提出了基于自相關函數的在線負載資源使用周期識別方法。應用自相關函數對在線負載資源序列的周期進行識別和量化,利用其周期性特征將長期資源預測轉化為周期間資源使用的比對統計。
(2)提出基于K-Means聚類的資源使用子序列分類方法。針對資源使用量以及變化趨勢,采用K-Means聚類算法對按照周期劃分的子序列集進行分類;最終依據分類,采用線性加權方法計算資源需求預測值。
(3)對本文提出的在線負載資源預測方法PRP進行了性能評測。實驗結果表明,與既有基于ARIMA算法、支持向量回歸算法和馬爾可夫模型的在線負載資源預測方法相比,PRP方法可使預測平均相對誤差最大降低28.3%,12.3%和27.4%。同時,隨著預測時間步長的增加,PRP方法在預測準確度和時間開銷上的優勢逐步增加。
2 在線負載周期性特征分析
本節將分析在線負載資源使用的周期性特征。
2.1 任務知識
請求到達波動性是在線負載的典型特征。隨著在線負載用戶群體的擴增、服務訪問或數據采集行為習慣的趨同,負載請求波動的周期性特征具有一定的普遍性。圖1中展示了3個不同的在線負載場景下請求強度的變化統計。

Figure 1 Examples of online workload user request/data arrival intensity圖1 在線負載用戶訪問量/數據到達強度
從圖1中可以分析出,在線負載請求強度呈明顯的周期性變化,在周期內數據呈相似的變化趨勢。以圖1a NASA網站1個月的用戶訪問量為例,其用戶訪問以24 h為1個周期發生變化,大多數周期內的用戶訪問量在500~8 000次以相似的趨勢波動。但是,也有少數周期內數據量變化有異常現象。其中,在第8和第9個周期內,用戶訪問量在0~4 000 波動,在第13個周期內,用戶訪問量最多達到了13 000以上。同樣,圖1b和圖1c分別展示了曼徹斯特大學的學生1周內對YouTube網站的用戶訪問情況和國內某互聯網公司的流式日志數據到達強度趨勢,其中流式日志業務是在線負載中典型的流式計算負載。除此之外,伯克利大學主頁訪問、法國世界杯體育網站[27]訪問等數據也均呈現為較典型的周期性特征。具體而言,上述在線負載的訪問具有如下共性特征:(1)負載請求以小時、天或者周為周期,具有相同的變化趨勢;(2)大多數周期間,數據的變化幅度相同或相似,存在少量周期間數據變化幅度有較大差異。
2.2 在線負載資源使用周期性特征分析
在線負載請求到達強度是影響其資源使用的核心因素,本文提出假設:周期性的用戶訪問/數據到達強度會引發在線負載的周期性資源使用特征。為此,通過1組實驗進行分析。
既有數據中心多采用容器技術部署在線負載,并進行資源隔離。因此,本文假設數據中心多在線負載間的資源使用干擾較小。基于容器技術,部署單在線負載,分析其資源使用特征。本文采用典型的Web類型負載——TPC-W,在數據中心單在線負載的場景下,設置用戶訪問量變化周期為1 h,周期內用戶訪問符合正弦分布,用戶訪問強度為40次/秒~120次/秒。
以上實驗展示了在周期性的用戶訪問強度下,在線負載資源使用變化的情況。分析可知,在用戶訪問強度變化以1 h為周期的情況下,其資源使用量的變化周期也為1 h。另外,在相同的用戶訪問強度下,每個資源周期內的數值波動范圍相同,周期間的變化趨勢也有較強的相似性。在第3個周期(圖2中橫坐標170~230),我們將請求強度變化從40次/秒~120次/秒提高到40次/秒~160次/秒,在圖2a中可以看到,在本周期內負載的內存使用量變化從1 700 MB~2 500 MB變為1 700 MB~2 700 MB,增長明顯。同樣,在第7個周期(圖2中橫坐標410~470),將線程變化從40次/秒~120次/秒降低到40次/秒~80次/秒,其內存和CPU使用量在第7個周期內也呈現明顯的降低。
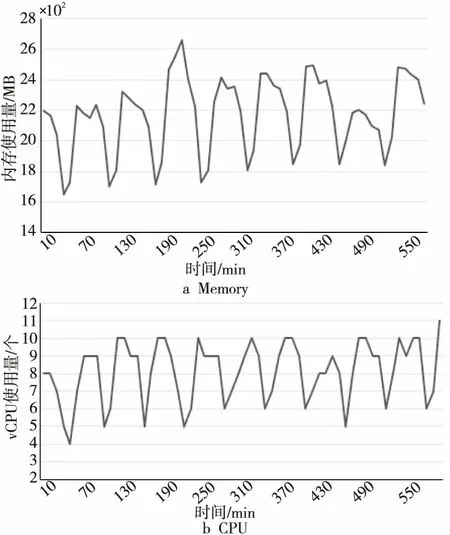
Figure 2 Variations in resource consuming of online services圖2 在線負載運行的資源使用情況
綜上,具有周期性請求/數據到達強度的在線負載,其資源使用量會隨著請求/數據到達變化,且呈現相近的周期特征。
3 基于周期性特征的在線負載資源預測方法PRP
本文將在線負載資源使用的周期性特征引入資源預測中。如圖3所示是在線負載資源預測方法PRP的框架。
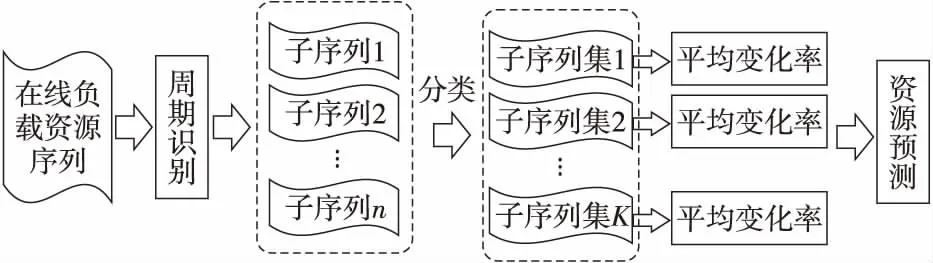
Figure 3 Overview of PRP圖3 在線負載資源預測方法PRP框架
PRP方法首先應用自相關函數法對在線負載資源使用量樣本序列進行周期識別;其次將樣本序列依據周期進行劃分得到子序列集;再次計算所有子序列間的相似度,并根據相似度進行子序列劃分;最終根據預測時刻點在各類子序列中對應時刻點的資源使用變化率計算資源需求預測值。
3.1 在線負載資源使用的周期識別
本文選用自相關函數方法對在線負載的內存和CPU資源使用量進行周期量化識別。自相關函數被廣泛用于信號的潛在周期性檢測中。對于1個有限長度的離散序列,當序列中2個變量存在關系時,隨著其中1個變量數值的確定,另1個變量會有不同的取值,但是該變量的取值有一定的規律性。這種統計規律可以通過自相關函數來表示,如式(1)所示:
(1)
其中,N是有限長的離散序列y的長度,x表示元素下標,k表示自變量。
自相關函數有以下性質:
性質1周期函數的自相關函數依然存在周期性,并且其周期性與原函數周期頻率相同。
性質2自相關函數具有偶函數特點,即R(k)=R(-k)。
性質3任意函數的自相關函數都會周期性地存在極大值和極小值,并且在相鄰的極大值和極小值之間,自相關函數是單調的。
本文的目的是利用自相關函數的特性計算出內存和CPU使用量序列的周期值。
由于內存和CPU的預測方法以及周期相同,因此,下面均以資源使用序列統一指代內存和CPU序列,L={l1,l2,…,ln},其中li表示第i個時間點對應的資源使用量,n為資源使用量樣本總數。具體的判別和度量流程如下所示:
方法1在線負載資源使用周期識別方法
(1)收集在線負載資源使用數據;
(2)以5 s為固定步長,截取樣本數據,構建在線負載資源序列ML;
(3)根據式(1)計算出序列ML的自相關序列MR;
(4)求取MR中任意2個相鄰的極大值,計算它們的時間距離t_maxi;
(5)將所有t_maxi求和,然后取平均值;
(6)所得到的平均值即為資源使用序列ML的周期。
3.2 在線負載資源使用樣本子序列分類
在線負載資源使用樣本子序列分類的目的是在序列周期識別的基礎上,統計具有不同資源使用量及變化趨勢的子序列類,最終為資源預測提供依據。
本文采用歐氏距離作為資源使用樣本子序列間相似度度量,稱為子序列距離,計算如式(2)所示:
(2)
其中,pi表示第i個序列,pj表示第j個序列,pik表示第i個序列中的第k個元素數據,同理,pjk表示第j個序列中的第k個元素數據。
顯然,子序列距離越大,序列間相似度越小,反之則序列間相似度越大。同時,本文采用聚類方法對資源使用樣本子序列進行分類。如第2節所述,在線負載資源使用的周期性特征呈現出多數周期間資源使用量值及變化幅度相同或相似,少數周期間則存在較大差異的特點。因此,本文將在線負載資源使用樣本子序列分為常規序列和異常序列。其中,常規序列是指在線負載資源使用子序列中數據變化范圍相似的大多數的子序列,異常序列是指在線負載資源使用子序列中數據變化發生異常的子序列。本文首先給出如下定義:
定義1全局子序列最大距離:所有資源使用樣本子序列之間距離的最大值dmax:
dmax=max({d(xi,xj)|xi∈X,xj∈X})
(3)
其中,d(xi,xj)表示xi、xj之間的距離,X表示樣本序列集合。
定義2全局子序列最小距離:所有資源使用樣本子序列之間距離的最小值dmin:
dmin=min({d(xi,xj)|xi∈X,xj∈X})
(4)
其中,d(xi,xj)表示樣本序列xi,xj之間的距離,X表示樣本序列集合。
定義3子序列類距離閾值:所有資源使用樣本子序列類中序列之間距離的最大值:
α=(dmax-dmin)×a+dmin
(5)
其中,0 本文選擇K-Means聚類算法[24]進行在線負載資源使用樣本子序列分類,它將1個給定的數據集劃分為用戶指定的k個聚簇,有著較高的執行效率。在線負載資源使用子序列分類的K-Means算法如算法1所示。 算法1在線負載資源使用子序列分類的K-Means算法 輸入:在線負載資源使用子序列集,子序列類距離閾值α,常規子序列占比閾值δ,子序列分類數K。 輸出:子序列分類集合C。 1C←?;/*初始化子序列分類集合*/ 2O←?;/*初始化中心點集合*/ 3 Fori 4oi←RandomSelect(X); 5O←O∪{oi}; 6 End For 7 Repeat: 8 ForxiinXDo: 9j←MinDistance(xi,O); 10Cj←Cj∪{xi}; 11 End For 12 Fori 13max_point_distancei←MaxDistance(Ci);/*計算每個簇內最大距離*/ 14maxD←maxD∪{max_point_distancei}; 15si←Scale(ni,N);/*計算每個簇內數據量占總的子序列數量比例*/ 16maxS←maxS∪{si}; 17 End For 18maxDistance←Max(maxD);/*計算所有簇距離的最大值*/ 19maxScale←Max(maxS);/*計算所有簇所占子序列總量比值的最大值*/ 20 UntilmaxDistance<α&maxScale>δ; 21 ReturnC 算法1依據用戶指定的子序列分類數量進行子序列聚類,從所有在線負載資源使用樣本子序列中隨機選取初始類簇中心點,并進行迭代計算。其迭代收斂條件有2個:(1)任一類簇中子序列的最大距離不超過定義的閾值,這保障了所獲得的子序列分類中,每一類子序列間具有相似的資源使用量和變化規律;(2)規模占比最大的類簇其規模占比應超過設定的比例閾值,這是因為根據本文第2節的觀測結果,在線負載資源使用周期性呈現出多數周期間資源使用量及變化規律相似,少數周期間差異較大的特點。通過約束規模占優子序列類的占比閾值,進一步保障聚類結果與實際場景中子序列分類情況吻合。 在周期識別和序列分類的基礎上,本節提出具有周期性特征的在線負載資源預測方法。 令NL={nl1,nl2,…,nlS}表示資源使用樣本集合,其中nli(1≤i≤S),表示第i類子序列集合,S是樣本類總量,nli={sli_1,sli_2,…,sli_K}表示按時間排列的第i類樣本子序列集合,K是序列類的總量。sli_j={eli_j_1,eli_j_2,…,eli_j_T},1≤j≤K,eli_j_t表示1個采樣周期內第t個采樣時刻的資源使用量,1≤t≤T,T是采樣周期時長。本文首先給出以下定義: 定義4子序列類比例:在經過周期分割的所有在線負載資源使用子序列中,每一類子序列所占子序列總數的比例,可以用式(6)表示: (6) 其中,|nli|為第i類子序列集合中的序列總數,S是樣本類的總量。 定義5子序列資源使用變化率:對任意子序列中采樣時刻t的資源使用變化率Rnli_j_t可表示為: (7) (8) 定義7子序列資源預測值:第i類子序列在下1個周期的采樣時刻t的資源使用預測值pli_t可表示為: pli_t=eli_K_t×(1+Anli_t) (9) 定義8在線負載資源預測值:最終的在線負載在下1周期t時刻的資源使用預測值lnext_t可表示為: (10) 其中,wi為第i類樣本子序列的預測權重。 由上述定義可知,對于在線負載資源需求的預測實質上是依據歷史資源使用樣本數據中各類樣本子序列出現的概率,對子序列中對應時間點的資源使用變化率進行加權平均,進而形成預測時間點相對于上1個周期相應時間點的資源使用變化率,最終計算出預測時間點的資源需求量。 本節從預測準確度和計算效率的角度對PRP方法進行性能評測。針對在線負載的主要資源需求,選取CPU和內存2類資源進行預測。 本文分別選取TPC-W和HiBench中的流式計算負載WordCount作為測試負載。上述負載分別是在線負載中Web服務和流式計算的典型代表。負載的請求/數據到達強度符合泊松分布和正弦分布。測試基礎環境由5臺服務器組成,服務器具體配置包括:Intel(R) Xeon(R) CPU E526600@2.20 GHZ*4,16 GB內存,1 TB磁盤,千兆以太網。實驗軟件環境主要包括Apache 2.4和Spark 2.3.1。實驗選取預測平均相對誤差(MRE)作為預測準確度的量化評價指標;選取預測時間開銷作為預測計算效率的量化評價指標。 Figure 4 MRE of memory utilization prediction of streaming workloads圖4 流負載內存資源預測誤差 實驗選取既有成果中基于ARIMA算法、馬爾可夫(Markov)模型以及支持向量回歸(SVR)的在線負載資源預測方法進行性能對比。這3種方法分別作為時間序列分析類和機器學習類方法被廣泛應用于在線負載資源預測問題,是較為有代表性的預測方法。 為了模擬長期預測,本文根據樣本中包含的采樣時刻點數量M,從第2M的時刻點開始對每隔30 s的資源需求進行預測,預測總量為100個時間點。 實驗選取WordCount作為流式計算負載,設置請求/數據到達服從泊松分布,通過配置不同的請求/數據到達強度以及變化周期構造不同的資源使用周期性特征,具體配置如表1所示。預測的樣本數據通過運行一段時間負載獲得,采樣周期為5 s,樣本規模分別為10 800,14 400,18 000。 圖4和圖5分別展示了在數據到達符合泊松分布的情況下,PRP方法和其他對比方法的預測平均相對誤差。由圖4和圖5可知,在各種數據到達強度-周期配置下,PRP的預測準確度均優于既有方法的,其中,CPU和內存資源預測平均相對誤差最大分別下降了25.4%和27.9%。同時,實驗顯示隨著樣本規模的減小,PRP的預測準確度優勢更為顯著。這是因為,PRP方法利用周期識別,將長期資源預測轉化為短周期內資源的比對預測,克服了既有方法對于大規模樣本數據的依賴。因此,PRP方法在樣本數據有限或長期預測的場景下具有較好的性能優勢。 Figure 5 MRE of CPU utilization prediction of streaming workloads圖5 流負載CPU資源預測誤差 Table 1 Data arrival and variation period settings 取值組數據到達強度/(MB/s)周期/min1[1,5]152[1,10]153[1,20]154[1,5]305[1,10]306[1,20]307[1,5]458[1,10]459[1,20]45 實驗選取TPC-W作為Web負載,請求到達同樣服從泊松分布。對于TPC-W負載通過改變請求發生數量來改變請求的到達強度。請求到達強度與周期設置如表2所示。預測樣本數據的獲取和規模同4.1節,預測樣本獲取、樣本數據規模以及預測時刻點的選取同4.1節。 Table 2 Request arrival intensity and variation period settings表2 請求到達強度變化和周期變化分組 圖6和圖7分別展示了在請求到達符合泊松分布的情況下,PRP方法和其他對比方法的預測平均相對誤差。由圖6和圖7可以獲得與4.1節相同的結論。對于Web負載,PRP可分別最大降低CPU和內存資源預測平均相對誤差22.6%和24.1%。 Figure 6 MRE of memory utilization prediction of web workloads圖6 Web負載內存資源預測誤差 Figure 7 MRE of CPU utilization prediction of web workloads圖7 Web負載CPU資源預測誤差 隨著樣本規模減小,PRP方法的預測性能優勢更為顯著。然而,相對于流式計算負載而言,Web負載的資源預測平均相對誤差平均上升了7.9%。這是由于TPC-W具有更為復雜的計算邏輯,對計算資源消耗的波動較流式WordCount負載更大,在資源使用樣本子序列分類數量受限的情況下,僅用較為簡單的線性加權方法計算資源預測值,無法更為精細地識別周期內資源使用的變化規律。 本節評測PRP和其他對比方法在不同的樣本規模下資源預測的計算效率。實驗選取流式WordCount和TPC-W作為測試負載,改變樣本規模統計預測所需的時間開銷。 對于流式WordCount,實驗設置數據到達強度為1 MB/s~10 MB/s,變化周期為20 min,數據到達符合泊松分布。實驗結果如圖8所示。 Figure 8 Time overhead of resource prediction of streaming workloads圖8 流式計算負載資源預測時間開銷 以請求到達強度變化為40次/秒~80次/秒、變動周期為20 min的TPC-W負載產生的資源序列為樣本數據的情況下,實驗結果如圖9所示。 Figure 9 Time overhead of resource prediction of web workloads圖9 Web負載資源預測時間開銷 在上述實驗中,PRP的預測平均相對誤差均小于其他比較方法的,最小下降率為9.3%(由于篇幅限制,本節不再列出預測準確度的測試數據)。然而,由圖8和圖9可知,隨著樣本數據規模的增大,PRP方法在預測過程中的時間開銷增長率平均為6.7%,而3種對比方法的時間開銷平均增長率分別為16.7%,19.6%和12.5%。這是因為PRP在第1次預測的過程中,已完成周期的識別,結合周期性特征,后面新增加的樣本數據不用再進行周期識別,減小了時間開銷。而在其他3種方法中,每1次建模和預測都要對全部的數據進行訓練,這樣才能保持一定的準確度。因此,隨著樣本的增大,其他3種方法的時間開銷明顯增加。 綜上而言,由于PRP充分利用了在線負載資源使用的周期性特征,將長期預測轉化為短周期的資源使用比對預測,因此避免了性能預測中的反復建模問題,在資源使用變化周期被識別后,僅通過簡單的周期間資源使用統計即可獲得預測值,同時保障了預測的準確性。 針對當前在線負載資源預測方法無法進行長期準確的預測和由于依賴海量樣本數據導致的較大的時間開銷問題,本文提出了一種基于周期性特征的在線負載資源預測方法PRP。該方法在分析提取在線負載資源使用周期性特征的基礎上,采用自相關函數方法量化計算在線負載資源使用周期,根據周期計算結果將資源使用樣本序列劃分成多個子序列;然后將子序列分類;最后加權綜合每一類子序列資源使用變化率,計算在線負載資源使用的預測值。大量的實驗表明,PRP方法在長期預測的準確度和時間開銷方面優于對比方法。 在進一步的研究工作中,將致力于提升樣本子序列分類精度,并在此基礎上使用更為復雜的資源預測方法進行預測。3.3 在線負載資源預測
4 性能測試與分析

4.1 流式計算負載資源預測準確度評測

表1 數據到達強度和周期變化分組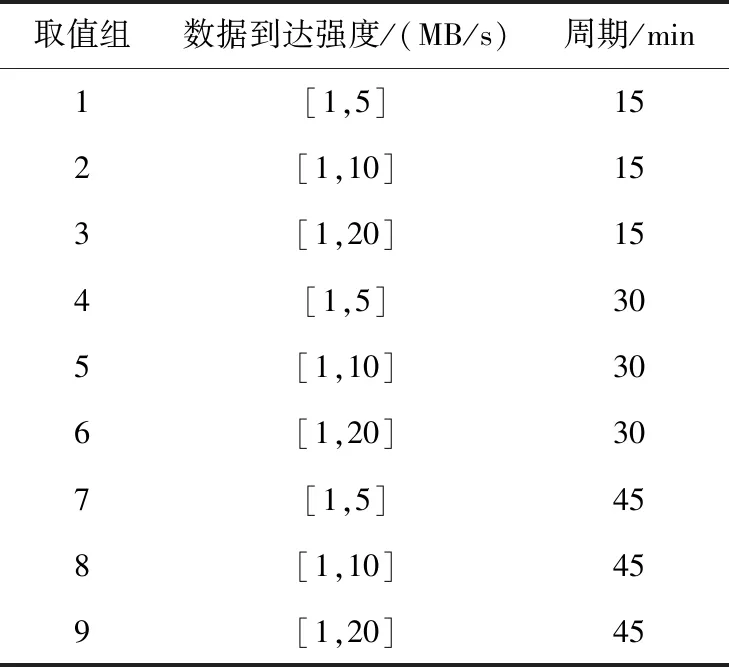
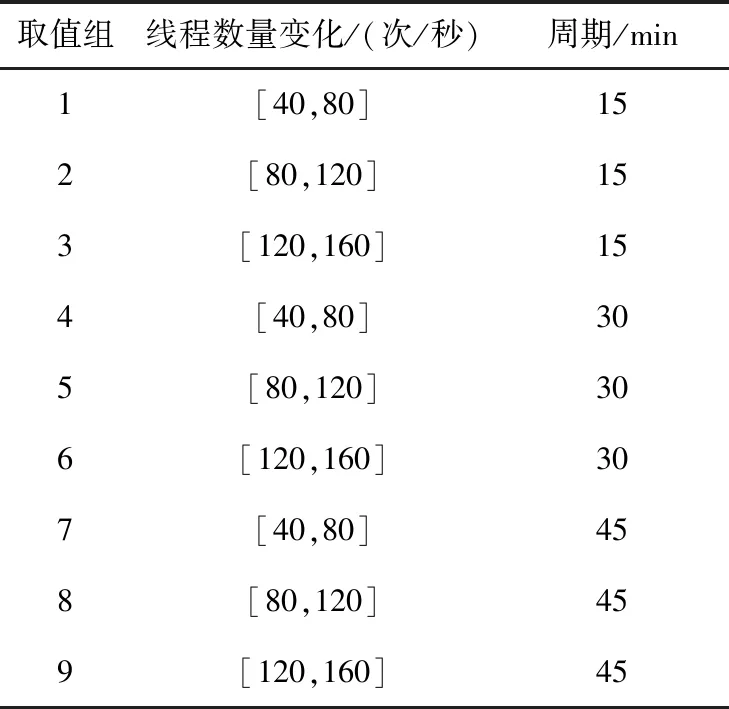
4.2 Web負載資源預測準確度評測
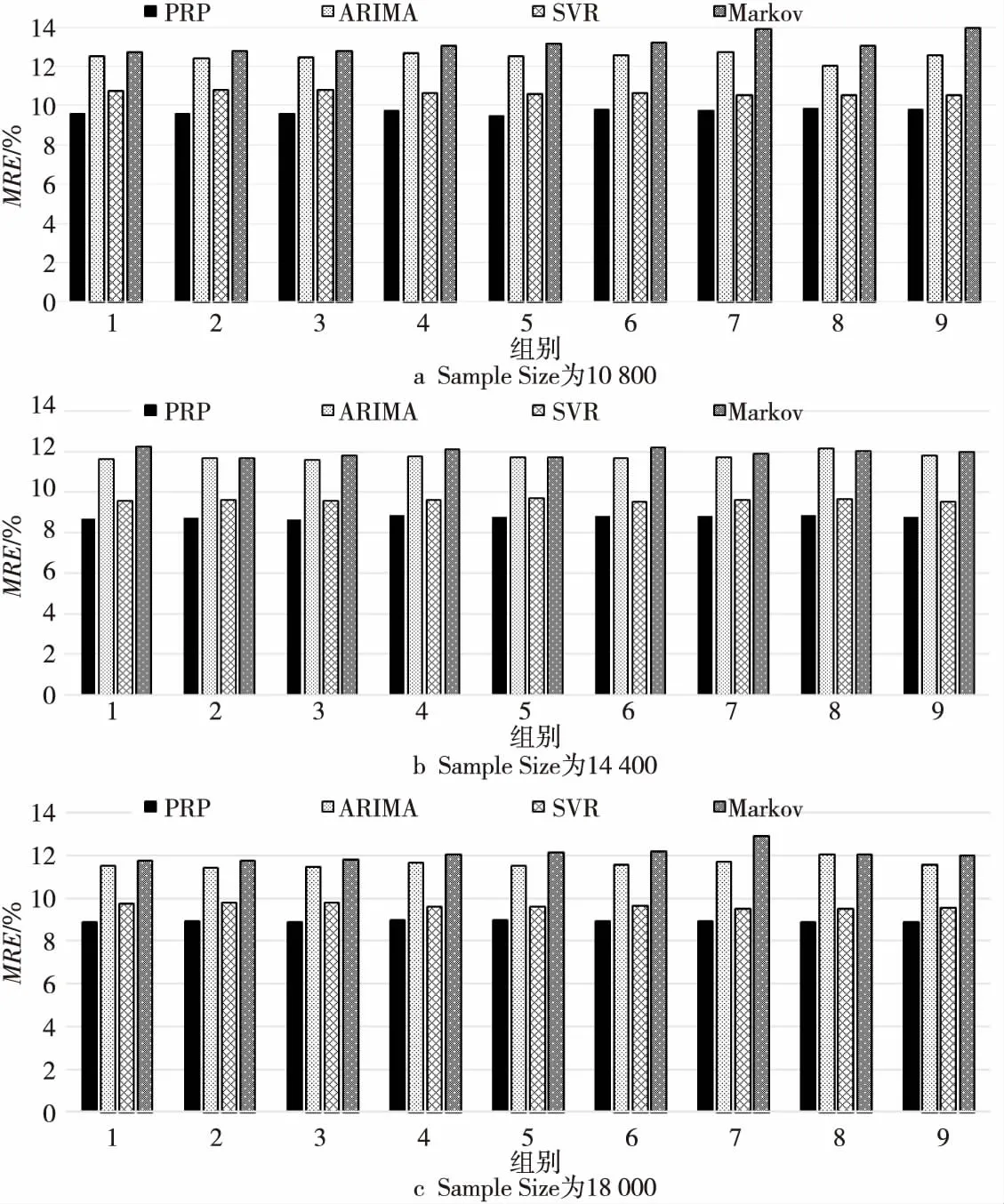
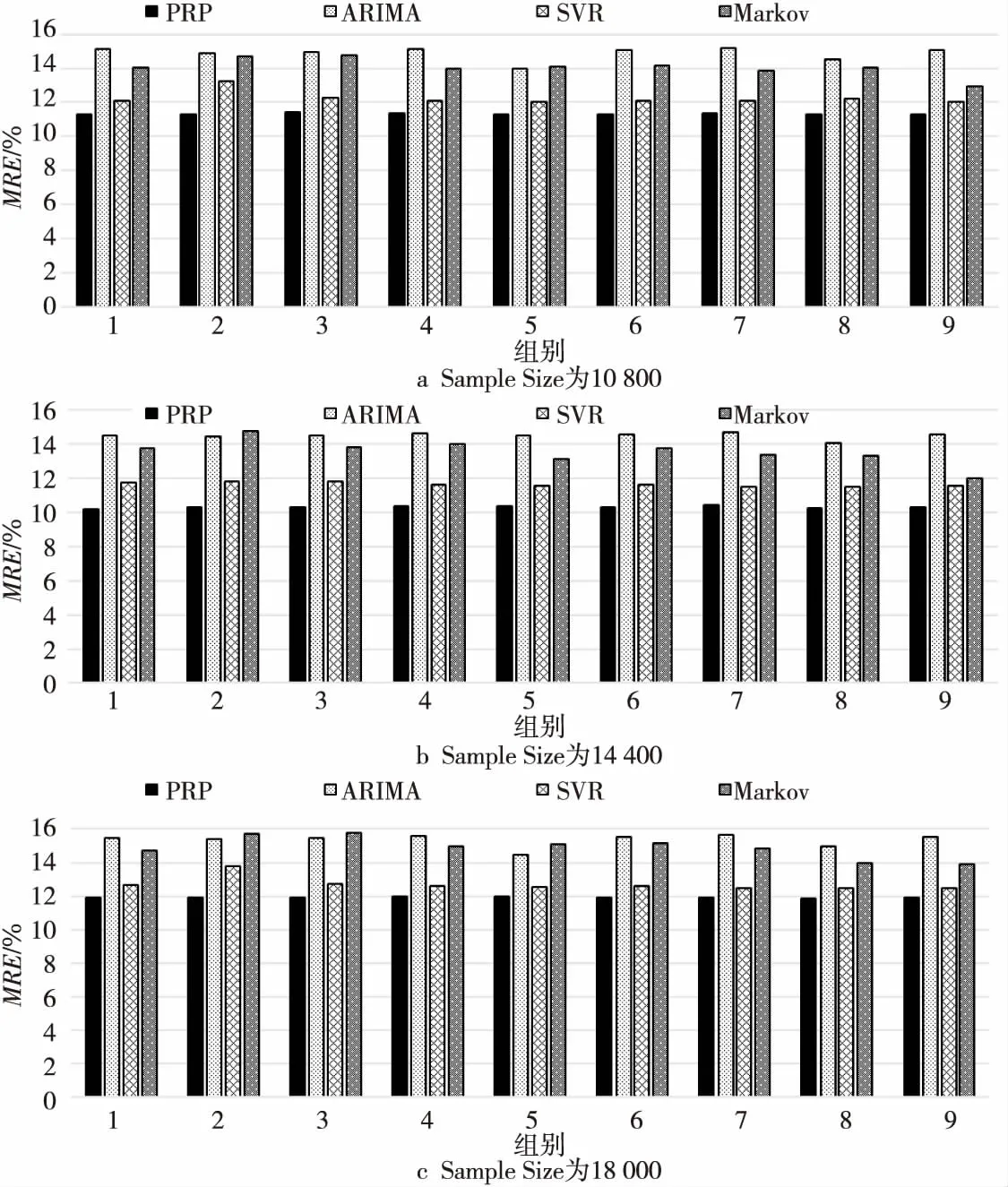
4.3 在線負載資源預測計算效率分析
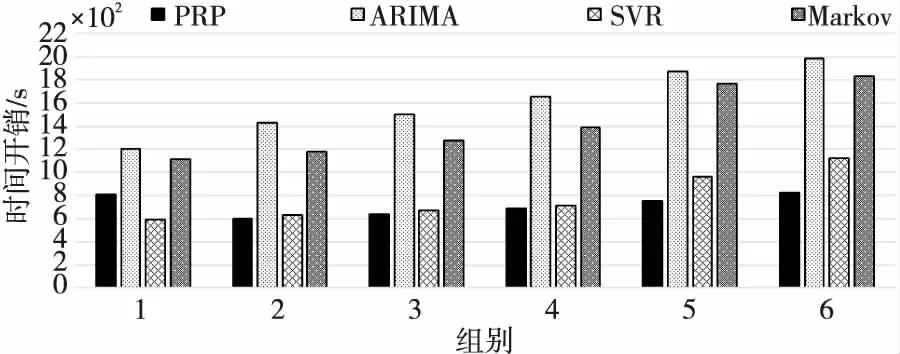
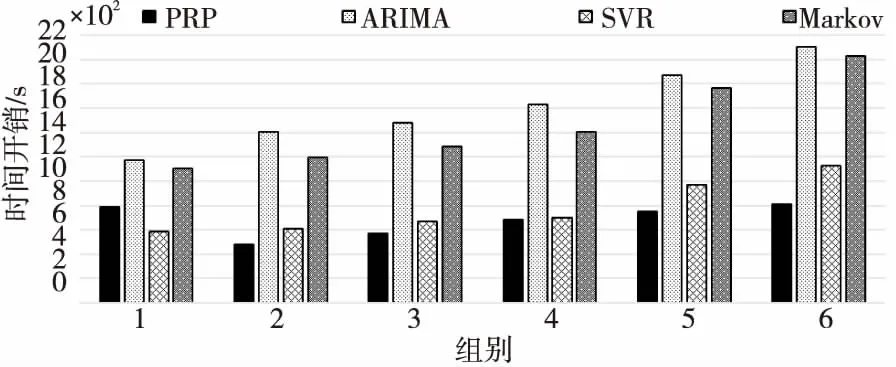
5 結束語

