基于改進蟻群算法的物流運輸路徑研究*

馬貴平,潘 峰

(西南交通大學希望學院，四川 成都 610400)

1 引言

隨著經濟和科學技術的發展，網上購物逐漸成為人們必不可少的生活方式，這種購物方式不僅大幅度便利了人們的生活，而且還帶動了物流行業的快速發展。物流作為“第三利益源泉”對經濟發展的影響日益明顯，越來越多的企業也紛紛加入其中，物流逐漸成為當今競爭激烈的行業之一。如何實現科學物流配送是每一家物流企業必須面對的一個非常繁瑣而且至關重要的難題，物流企業都需要在運輸過程中實現低成本、高效率的目標。在物流配送中，物流運輸路徑的選擇問題尤為關鍵，它是每一家物流企業都需要解決的難題。在物流運輸過程中，降低企業物流成本，縮短運輸時間，提升運輸服務質量，獲得運輸最優路徑是學者們研究的目標。為此本文提出基于改進蟻群算法的物流運輸模型來降低物流運輸成本,提高運輸效率。

2 車輛路徑優化的問題

車輛路徑優化問題VRP(Vehicle Routing Problem)是物流配送優化過程中的重要研究對象，車輛路徑優化問題被明確定為NP-hard問題，隨著配送貨物數量不斷增加，傳統路徑規劃算法并不能在較短時間內獲得最優解，這類組合優化問題利用仿生優化算法能更好地進行求解。國內外學者都提出了大量的算法對該類問題進行求解,例如王迎等[1]提出一種加入混沌擾動的模擬退火蟻群算法CSAACO(Chaotic-Simulated Annealing Ant Colony Algorithm)，該算法設定了尋找的范圍，對信息素更新方式加以改進，提高了算法的全局尋優能力，在求解效率和精度方面優于傳統蟻群算法；龍汀等[2]提出利用蟻群算法的思想求解VRP問題，該思想利用一種改進的蟻群算法來求解帶時間窗的VRP，通過加入偽隨機等相關參數來改進傳統蟻群算法，最后通過仿真模擬實驗測試，實驗結果表明該算法能有效獲得全局最優解，加快算法收斂速度；趙美紅[3]在標準蟻群算法基礎之上，對信息素更新方式進行改進，并且加入最近鄰域算法以及局部最優搜索策略來解決算法初期的螞蟻路徑選擇問題，同時利用動態信息素更新方法對標準蟻群算法進行優化改進，使算法趨于全局收斂，實驗表明算法的性能得到了有效提高；王蕾等[4]搭建了多子群蟻群算法，利用各子區間之間的信息排斥與依存關系，加快最優線路的搜索速度，縮短了運行任務所需要的時間。

物流路徑優化的問題是一個典型的組合優化問題，是極為復雜的系統性問題，上述研究在一定程度上改善了該難題。本文在以上研究基礎之上，提出采用改進蟻群算法來有效改進目前運輸車輛在選擇路徑時存在成本高、效率低下等問題，并與文獻[1]中的CSAACO算法和傳統的蟻群優化ACO(Ant Colony Optimization)算法進行仿真實驗對比，來驗證本文改進算法的可行性和有效性。

3 傳統蟻群算法

ACO算法是一種人工智能優化算法，用以模擬自然界蟻群在搜尋食物過程中探索線路的行為。蟻群優化算法表明螞蟻能夠根據前面螞蟻所分泌的信息素來選擇路徑，其選擇食物源線路的通往概率與該線路上分泌的信息素強度成正比。因此，在螞蟻經過的路徑上會形成一種信息的反饋現象，即選擇某1條路徑的螞蟻數量越多，該路徑上所留下的信息素就越多，后面的螞蟻選擇該條路徑的可能性就越大，以此達到尋找到最短路徑的目的。

假設有m只螞蟻，并且螞蟻全部從規定出發點出發，假設它們到達食物的道路上分布有n個節點，τij(t)表示節點i和節點j之間的路徑上在t時刻的信息素濃度，ηij(t)為路徑i→j對應的啟發信息函數，則對某1只螞蟻k，從節點i爬行到下1節點j的概率為：

(1)

τij(t+1)=(1-ρ)τij(t)+Δτij(t)

(2)

(3)

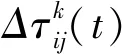
4 改進蟻群算法模型

傳統蟻群算法優點較多，如算法魯棒性較強，采用正反饋算法，并且容易和其他算法相結合等。但是，傳統蟻群算法也不可避免地存在一些缺陷，例如，容易陷入局部最優解而導致搜索停止現象，而且搜索時間較長，在解決車輛路徑優化這類NP-hard問題時，傳統蟻群算法尋求最優解的速度和效率就會變得相對較低。在應用傳統蟻群算法優化物流運輸路徑過程中,常見的方法是求解出物流運輸起始點到終點之間的最短距離,此類算法主要考慮的是利用路徑長短來衡量解的優劣。但是，在物流運輸過程中，有必要考慮所選擇道路的平均通暢程度，所產生的運輸成本以及運輸時間等因素。因此，道路的選擇其實是1個多約束條件下的求最優解的問題。為此，本文在標準蟻群算法基礎之上，加入基于多個約束條件的最優路徑選擇的改進蟻群算法，在傳統蟻群算法基礎之上對啟發函數和信息素更新方式分別進行改進，利用下1節點到終點的距離來改進蟻群算法中的啟發函數；通過由物流運輸時間因子、物流運輸成本因子和道路平均通暢程度因子組成的約束函數模型來改進算法中的信息素更新方式。改進后的蟻群算法使得物流運輸時間更短，運輸途徑更短，運輸效率更高。

5 改進啟發信息模型

在傳統蟻群算法公式中，啟發函數只考慮相鄰2個節點之間的距離的倒數1/dij，但這樣的方式只反映了當前節點與相鄰節點的關系，沒有反映當前節點和目標點的關系。這種局部的搜索范圍是以當前節點為中心，周圍節點為半徑的類似圓形的區間，這種沒方向性的搜尋方式容易讓螞蟻陷入局部最優，只能搜索出局部最短路徑，而且容易導致得到的解并非全局最優路徑，從而失去了全局搜尋最優解的能力。針對該問題，可將下1個節點j與終點g之間的直線距離加入到啟發函數中，表達式如下所示：

(4)

其中，dij表示當前節點i到下1個節點j之間的距離，djg表示當前節點j到節點g之間的距離。將下1節點和終點之間的距離引入啟發函數，增強了螞蟻搜尋的目的性，可加快算法收斂速度。若djgdij,則規定節點j為近距離節點。當螞蟻搜索時，對于遠距離的節點無需搜索，只需計算距離i較近的幾個節點，利用此改進方法，能夠進一步減少計算量，加快算法收斂速度。因此，利用式(5)對傳統蟻群算法進行改進：

(5)

5.1 改進信息素更新模型

基于物流運輸過程中，最優路徑的選擇主要考慮幾個關鍵因素：運輸的時間、成本、道路平均通暢程度。為了更快獲取最優解，本文通過設置運輸時間因子、運輸成本因子、道路平均通暢程度因子來對路徑選擇建立基于多個約束因子的數學模型X(j)，并將該模型融入到標準蟻群算法當中,實現基于多約束條件的路徑實時更新和動態選擇,引導物流運輸選擇朝最優路徑前行,更加精確地得到最優解。

5.1.1 物流運輸時間因子

(6)

其中，Tjmax表示物流在道路運輸過程中允許的預估最長時間上限，Tj表示物流運輸所需的實際時間，并且

Tj≤Tjmax

(7)

X1(j)為物流運輸時間因子，表示物流運輸到節點j的實際運輸時間與預估最長時間的比值。該比值越大，說明實際運輸時間越長。

5.1.2 運輸成本因子

(8)

其中，X2(j)表示運輸成本因子，表示物流運輸到節點j的實際運輸成本fj與最大預估運輸成本fj max的比值，該比值越大，說明實際運輸成本越高。

fj=abrasionj+Tollj+Fuelj

(9)

fj≤fjmax

(10)

其中，abrasionj表示道路運輸過程中的磨損費；Tollj表示通行費；Fuelj表示燃料費。

5.1.3 道路平均通暢程度

(11)

其中，X3(j)表示物流運輸到節點j的過程中，運輸到節點j的路徑的通暢程度與車輛行駛道路通暢度最低容忍度的比值，該比值越大，說明運輸車輛選擇該路徑行使過程越通暢;Clj表示運輸到節點j的路徑的通暢程度;Cljmax表示車輛行駛道路通暢度的最低容忍度。

綜上，約束函數X(j)表示如下:

X(j)=εX1(j)+φX2(j)+γX3(j)

(12)

其中,X1(j)表示物流運輸時間因子，X2(j)表示物流運輸成本因子，X3(j)表示道路平均通暢程度因子，ε、φ、γ分別表示在物流運輸到節點j的過程中所花時間、成本、道路平均通暢程度所占權重。

5.1.4 最優最差路徑優化

為了加快算法的收斂速度，對質量路最差的徑進行削弱，加入懲罰因子，降低其被選擇的概率，增強質量較好的路徑上的信息素濃度，使螞蟻選擇質量更佳的路徑。對標準蟻群算法中信息素更新公式改進如下：

(13)

式(13)中引入參數μ，μ∈[0,1]，Dbest表示遍歷到的最優路徑，|Dbest|表示其長度，Dworst表示遍歷到的最差路徑，|Dworst|表示其長度,ρ為信息素濃度揮發系數。μ表示改進蟻群算法中的信息素增強因子，對遍歷到的最差路徑進行懲罰，降低其信息素濃度，對遍歷到的最優路徑上的信息素進行增強。同時，在改進蟻群算法執行過程中，為了防止路徑上信息素濃度無限制地累加，必須對信息素濃度進行限制，約束表達式如下所示：

(14)

其中,τmax，τmin分別表示信息素最大值和最小值。

6 改進后蟻群算法流程

改進后的蟻群算法流程圖如圖1所示。

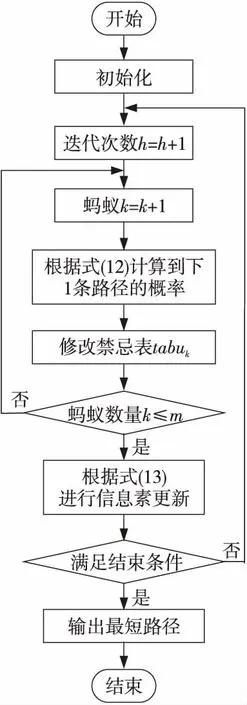
Figure 1 Flow chart of improved ACO algorithm圖1 改進ACO算法流程圖

7 仿真實驗

在仿真實驗中,具體的實驗環境設置如下:CPU 為2.30 GHz，內存為4 GB，操作系統為Windows 2003，采用 Matlab 7.0實現編程。改進后的蟻群算法參數設定為：螞蟻數量為100，初始的信息啟發因子α=1，期望啟發因子β=1，信息素揮發系數ρ=0.5，ε=1/3，φ=1/3，γ=1/3，最大的迭代次數為300次，采用快遞物流公司的5個配送網點的數據，其物流配送服務的客戶規模如圖2和圖3的橫坐標所示，配送時間縮短量和配送距離縮短量如圖2和圖3中的縱坐標所示。采用本文改進的蟻群算法、ACO算法和CSAACO算法分別對物流運輸車輛進行最優路徑求解，求解結果用圖2和圖3中的折線表示。

從圖2可以看出,改進算法的平均尋優路徑的時間比ACO算法和CSAACO算法的分別縮短258 004 s和15 000 s；當客戶規模在100～200時，傳統的ACO算法、CSAACO算法和本文的改進算法的任務時間方面差異不是那么明顯，當隨著客戶規模不斷增加，在執行同樣規模任務的情況下，本文算法的時間遠低于CSAACO和ACO的，本文算法能夠彌補CSAACO算法和ACO算法的尋優時間較長的不足，具有更快的求解速度。

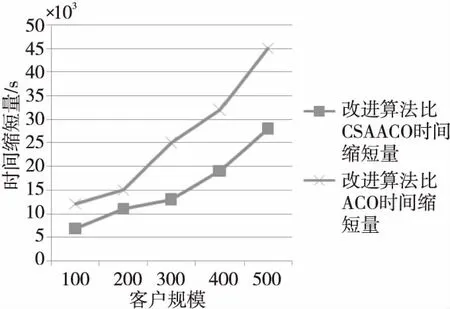
Figure 2 Relationship between customer size and time shortening圖2 客戶規模與時間縮短量的關系

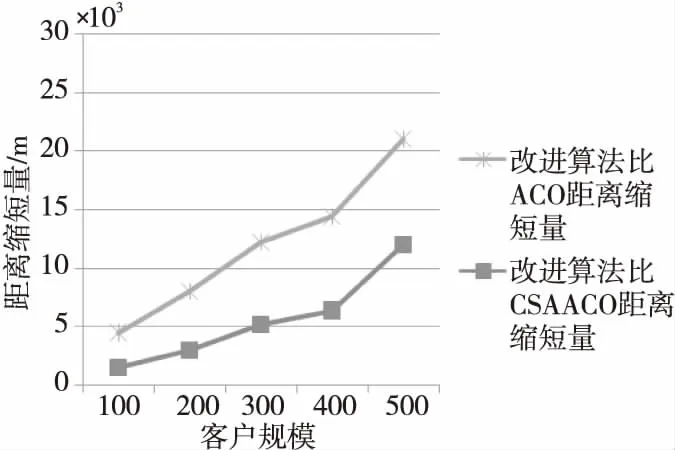
Figure 3 Relationship between customer size and distance reduction圖3 客戶規模與距離縮短量的關系

從圖3可以看出,本文改進算法的求解路徑距離相比ACO和CSAACO分別減少25 000 m和5 854 m。當客戶任務規模為100時，本文算法與CSAACO算法相比，距離縮短了約2 650 m；改進算法與傳統ACO算法相比，距離縮短了約5 000 m；而且隨著規模的增加，差距在逐漸擴大，本文改進算法表現出來的優勢更加明顯，具有更好的路徑尋優能力。

以上實驗結果表明，改進算法在尋優效率和尋優質量方面相比于CSAACO算法和ACO算法都有著明顯的提升。特別是隨著服務客戶的規模不斷擴大，該算法能更有效地解決物流配送耗時長和求解質量差等問題，優勢得到了更好的體現，利用本文改進蟻群算法在同樣客戶規模任務的情況下，能夠有效縮短執行配送任務的時間，減少運輸路徑距離，加快算法收斂速度，最大化地提高物流行業整體配送效率。

8 結束語

物流運輸的路徑選擇問題對物流企業的運送成本、時間與效率的影響至關重要，是所有物流行業所面臨的難題。本文在傳統蟻群算法基礎之上對路徑上的信息素濃度進行限制，同時加入基于運輸時間、成本、道路平均通暢程度因子的約束條件，改進信息素更新方式，從而改變了物流路徑轉移概率，增加了全局尋優能力，縮短了配送路徑，降低了物流企業配送所花費的成本，提高了配送效率，促進了物流行業的快速發展。