可證安全的隱私保護多接收者異構聚合簽密方案*

劉祥震，張玉磊，郎曉麗，駱廣萍，王彩芬

(1.西北師范大學計算機科學與工程學院,甘肅 蘭州 730070;2.深圳技術大學,廣州 深圳 518000)

1 引言

傳統公鑰密碼常采用數字加密保護方案的機密性，用簽名技術來保證對簽名的認證性。數字簽密[1]提出之前，研究人員通常使用先簽名后加密的方法，來確保方案的機密性和不可偽造性，但這種方法不僅計算量大，而且通信代價也高。簽密是將加密和簽名同時進行的一種技術，在實現原有功能的基礎上提升了效率。聚合簽名將用戶產生的多個簽名批量驗證，從而降低了驗證開銷。

聚合簽名是由Boneh等人[2]在2003年提出的。2004年，HyoJin等人[3]提出了批量驗證的聚合簽名方案，隨后Shim[4]指出HyoJin方案只能保證單個簽名的安全，不能保證聚合后的簽名安全性。Song等人[5]將聚合簽名應用到車載網中，但是提出的方案簽名可以被偽造。2009年，Sharmila等人[6]首度給出了聚合簽密的具體方案，該技術具有簽密以及聚合驗證的功能。

2012年，Ren等人[7]設計了基于身份密碼體制下可證安全的聚合簽密方案，但是該方案不支持公開驗證。2014年，Ziba等人[8]把聚合簽密技術應用到無證書密碼體制中。很多工業部門開始使用物聯網，傳輸過程中可能會使用不同的密碼技術。有些使用傳統公鑰體制TPKI(Traditional Public Key Infrastructure)，有些使用基于身份的密碼IBC(Identify-Based Cryptography)和無證書公鑰密碼CLC(Certificateless Public Key Cryptography)。如果發送方和接收方屬于2個不同密碼體制，若要進行系統間的通信，就需要用到異構技術。Sun等人[9]在2010年設計了異構簽密體制。2011年，Huang等人[10]構造了異構體制下IBC→TPKI方向的簽密方案。2013年，Fu等人[11]根據文獻[9]方案，設計了多接收方的IBC→TPKI異構簽密方案；隨后，Li等人[12]設計了異構密碼體制下的雙向TPKI?IBC簽密方案。2016年，劉景偉等人[13]設計了異構體制下高效的TPKI→IBC方案。張元英[14]在2017年設計了異構體制下CLC→IBC方向的簽密方案。牛淑芬等人[15]聯合聚合簽密與異構體制，設計了TPKI→IBC的異構聚合簽密方案。2018年，張玉磊等人[16]提出了異構雙向IBC?CLC聚合簽密技術。

2018年，牛淑芬等人[17]設計了異構密碼體制下多接收方的聚合簽密方案，但是該方案存在CLC下AΙΙ敵手KGC(Key Generation Center)被動攻擊。為了解決原方案中存在的安全漏洞，本文構造出安全的隱私保護多接收者異構簽密方案，首先在第2節給出了原方案及其具體的安全性分析。在第3節，指出牛淑芬方案出現安全缺陷的原因并在原方案基礎上設計了改進方案。在第4節中，通過安全性證明表明了單密文和聚合后密文的不可偽造。

2 文獻[17]方案及安全性分析

2.1 文獻[17]方案回顧

文獻[17]包括以下幾個算法：

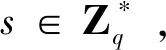
(2)CLC-KG：CLC系統中的發送方Si(i∈{1,2,…,m})通過以下方式進行身份匿名并產生公私鑰。

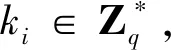
(3)IBC-KG：PKG為IBC系統中的接收方IDrj(j∈{1,2,…,n})計算私鑰Drj=sQrj，其中，Qrj=H1(IDrj)。

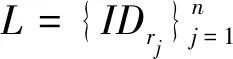
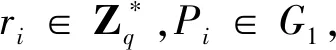
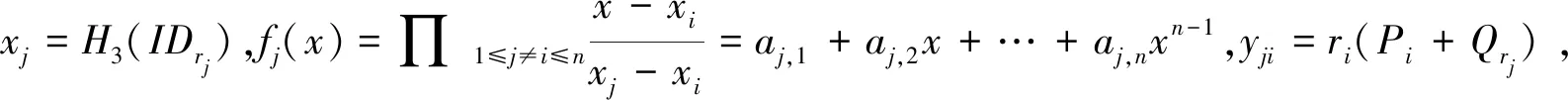
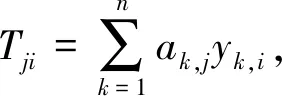
④計算hi=H4(Ci,Ri,PSi,IDSi)，Si=DSi+(XSi+hiri)Q。

⑤接收方收到Si發送的密文σi=(Ri,Ci,Ti,Si)。

(5)解簽密：接收密文σi(i∈{1,2,…,m})后，使用IDrj(j∈{1,2,…,n})進行解簽密。

①計算QSi=H1(IDSi)，hi=H4(Ci,Ri,PSi,IDSi)。

②檢查等式e(Si,P)=e(QSi,Ppub)e(PSi+hiRi,Q)是否成立,若成立，則密文σi有效；否則結束。

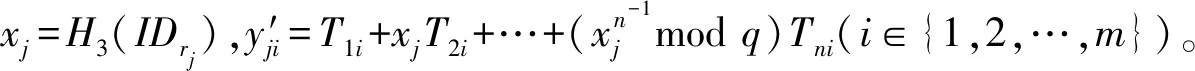
④計算w′i=e(Ppub,y′ji)e(Ri,Drj)-1。

⑤恢復消息Mi=H2(w′i)⊕Ci。

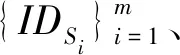
(7)聚合解簽密:

①計算QSi=H1(IDSi)，hi=H4(Ci,Ri,PSi,IDSi)。

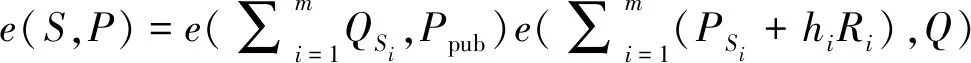
2.2 安全性分析

本文給出2種具體攻擊過程來展示文獻[17]中單個簽密與聚合簽密均可被偽造。

文獻[17]方案為CLC→IBC異構聚合簽密方案。對IBC系統中的安全主要考慮機密性；對CLC系統中的安全主要考慮敵手AΙ與AΙΙ對密文的不可偽造性。其中，AΙ可更替用戶公鑰，但是無法得到系統的主密鑰；AΙΙ為惡意KGC，能得到主密鑰，無法更替用戶的公鑰。通過分析發現，AΙΙ可偽造文獻[17]的單簽密密文和聚合簽密密文。

2.2.1 偽造單簽密密文

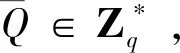
(2)詢問階段:AΙΙ通過H2、H4詢問來獲取h′i的值。

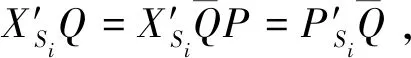
(4)偽造的單個密文正確性。

IBC系統中收到AΙΙ發送的密文σ′i=(R′i,C′i,Ti,S′i)，首先計算QSi=H1(IDSi),h′i=H4(C′i,R′i,PSi,IDSi)。驗證等式e(S′i,P)=e(QSi,Ppub)e(P′Si+h′iR′i,Q)，檢查密文σ′i。

其中

e(QSi,Ppub)e(P′Si+h′iR′i,Q)

AΙΙ偽造的單個簽密密文通過驗證等式。所以，文獻[17]方案不滿足單個簽密密文的不可偽造性。

2.2.2 對聚合密文進行偽造

敵手AΙΙ偽造聚合密文：

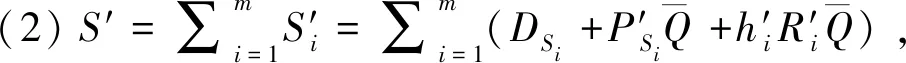
(3)驗證偽造的聚合密文：

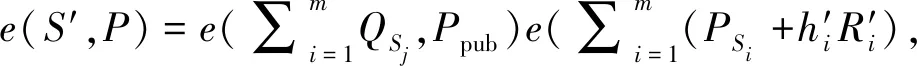
其中

敵手AΙΙ偽造的聚合密文通過驗證等式。所以，文獻[17]方案不滿足聚合簽密密文的不可偽造性。

3 改進的異構簽密方案

文獻[17]方案中不可偽造性不安全的原因在于G1的2個不同生成元P,Q，且CLC系統中的AΙΙ知道系統主密鑰與用戶部分私鑰，因此可以很容易計算出XSiQ,riQ。

我們這里所講的“親子”是廣義的，即把學生分成若干小組，每個小組六至七人，由一名家長組織，帶領學生共同閱讀。親子閱讀旨在讓家長根據兒童心理發展的特點，通過各種生動有趣的方法引導孩子對閱讀過程產生興趣，從而培養學生良好的自主閱讀能力。親子閱讀是一種傳授有關閱讀技能、方法的行為，它能夠激發學生的好奇心和強烈的閱讀興趣，發展學生語言、智力等方面的能力，真正達到早期閱讀的目的。

(2)CLC-KG：CLC系統中的Si(i∈{1,2,…,m})通過以下過程匿名并產生公私鑰:

(3)IBC-KG：PKG為IBC系統中的接收方IDrj(j∈{1,2,…,n})計算私鑰Drj=sPkrj，其中，Pkrj=H1(IDrj)。

①對消息進行加密：隨機選取δ∈{0,1}n，計算ri=H2(δi,Mi)，Ri=riP，wi=e(Ppub,P)ri，Ci=H3(wi)⊕Mi。

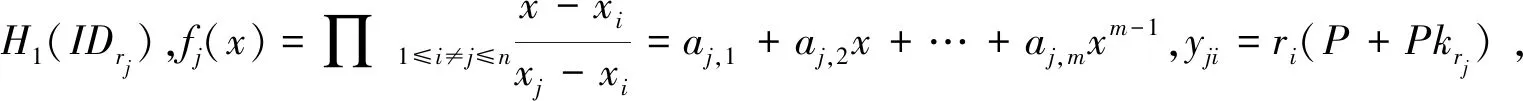
③發送方對消息進行簽名：計算hi=H4(Ci,Ri,PkSi,IDSi)，Si=DSi+(xi+hiri)H5(Ri)。

④Si將密文σi=(Ri,Ci,Ti,Si)發給接收方。

(5)解簽密：接收密文σi(i∈{1,2,…,m})后，利用IDrj(j∈{1,2,…,n})進行解簽密。

①計算hi=H4(Ci,Ri,PkSi,IDSi)。

②驗證簽名的有效性：檢查等式e(Si,P)=e(QSi,Ppub)e(PkSi+hiRi,H5(Ri))是否成立，若成立，密文σj有效，則計算以下步驟；否則結束。

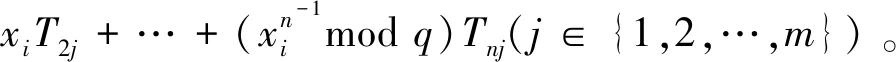
④計算w′i=e(y′ij,Ppub)e(Ri,Drj)-1。

⑤解密消息：恢復消息Mi=H3(w′i)⊕Ci。

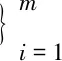
(7)聚合解簽密：

①計算hi=H4(Ci,Ri,PkSi,IDSi)。

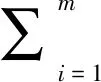
正確性分析如下：

(1)單個簽名驗證。

e(Si,P)=e(DSi+(xi+hiri)H5(Ri),P)=

e(DSi,P)e((xi+hiri)H5(Ri),P)=

e(QSi,sP)e(xiH5(Ri),P)e(hiriH5(Ri),P)=

e(QSi,Ppub)e(PkSi,H5(Ri))e(hiRi,H5(Ri))=

e(QSi,Ppub)e(PkSi+hiRi,H5(Ri))

(2)聚合簽名驗證。

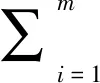
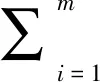
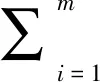
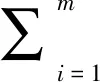
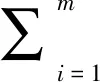
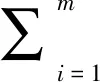
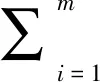
4 改進方案的安全性分析

改進方案的目的在于提高原方案的不可偽造性。該方案的不可偽造性包括單簽密密文的不可偽造性與聚合簽密密文的不可偽造性，其安全模型同文獻[17]。

4.1 單簽密密文不可偽造性

定理1若CDH問題困難，改進方案在隨機預言模型下存在AΙ和AΙΙ自適應選擇消息攻擊下不可偽造是安全的。

引理1隨機預言模型下的AΙ以優勢ε擊破本文方案，則挑戰者C就能以ε′≥(ε-qS/2k)(1-1/qppk)qppk優勢解決CDH問題，其中，部分私鑰詢問與簽密詢問的訪問次數分別為qppk與qS。

證明C規定CDH問題(P,aP,bP)，計算abP。

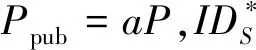
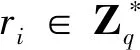
(4)H3詢問：C收到對H3的詢問時，C選取任意w2i∈{0,1}n作為返回值。

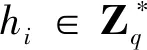
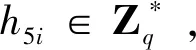
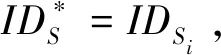
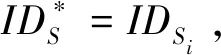
(9)公鑰詢問：當AΙ詢問IDSi的公鑰時，C查找表LPk，若表中存在，將PkSi發送給AΙ；否則，從表Lx中查找秘密值xi，計算PkSi=xiP，并發送給AΙ。將(IDSi,PkSi)存于表LPk中。

(10)公鑰替代詢問：當AΙ把IDSi的公鑰PkSi替代成Pk′Si時，C把表LPk中的元組(IDSi,PkSi)替代成(IDSi,Pk′Si)，同時把IDSi秘密值設置成xi=⊥。

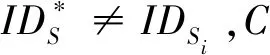
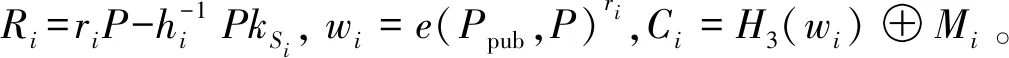
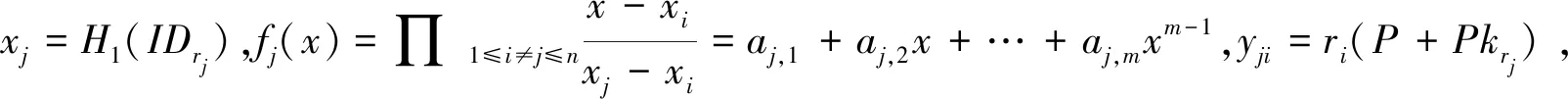
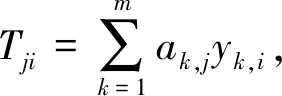
④計算Si=DSi+hiriH5(Ri)。

⑤最后C把密文σi=(Ri,Ci,Ti,Si)發送給敵手AΙ。

□

引理2隨機預言模型下的AΙΙ以不可忽略的優勢ε擊破本文方案，則存在挑戰者C，能以ε′≥(ε-qS/2k)(1-1/(qSk+m))qSk+m-1優勢解決CDH問題，其中，部分私鑰詢問、簽密詢問的訪問次數分別為qppk與qS。

證明C規定CDH問題(P,aP,bP)，計算abP。

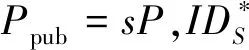
(2)H1、H2、H3詢問，秘密值詢問同引理1。

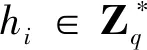
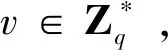
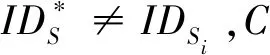
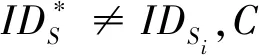
所以

C通過計算輸出了abP作為CDH問題的解。

□

4.2 聚合簽密密文不可偽造性

定理2若CDH問題困難，本文方案在隨機預言模型下存在敵手AΙ和AΙΙ自適應選擇消息攻擊下不可偽造是安全的。

引理3隨機預言模型下AΙ以不可忽略的優勢ε擊破本文方案，則存在挑戰者C，能以ε′≥(ε-qS/2k)(1-1/qppk)qppk優勢解決CDH問題，其中，部分私鑰詢問、簽密詢問的訪問次數分別為qppk與qS。

證明挑戰者C設置系統參數，其中Ppub=aP。詢問階段與引理1相同。

□

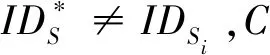
引理4隨機預言模型下的AΙΙ以不可忽略的優勢ε擊破本文方案，則存在挑戰者C，能以ε′≥(ε-qS/2k)(1-1/(qSk+m))qSk+m-1優勢解決CDH問題，其中，部分私鑰詢問、簽密詢問的訪問次數分別為qppk與qS。

證明挑戰者C設置系統參數，其中Ppub=sP。詢問階段與引理2相同。

C通過計算輸出了abP作為CDH問題的解。

□

5 性能分析

5.1 效率分析

首先，所有方案選擇相同的系統參數，包括群G1與G2，對n個消息聚合。將本文改進方案與文獻[15-17]在簽密與解簽密計算代價、是否保護用戶隱私、不可偽造4個方面進行比較，結果如表1所示。其中，U、O、f分別表示G1中乘法、雙線性對以及指數運算。

Table 1 Comparison of efficiency 表1 效率比較

通過數值理論分析發現，在簽密階段，文獻[15]方案有4n個乘法運算，而本文方案有2n+5個乘法運算；相較于文獻[16]，本文方案在增加了乘法的基礎上減少了指數運算；與文獻[17]相比，本文方案在不增加計算時間量的同時實現了不可偽造性的安全需求。

5.2 實驗仿真

利用雙線性對包對所提方案中的簽密算法與解簽密算法進行了實驗仿真。接收方人數分別為100,200,…,1 000。簽密時間與解簽密時間的仿真結果分別如圖1和圖2所示。

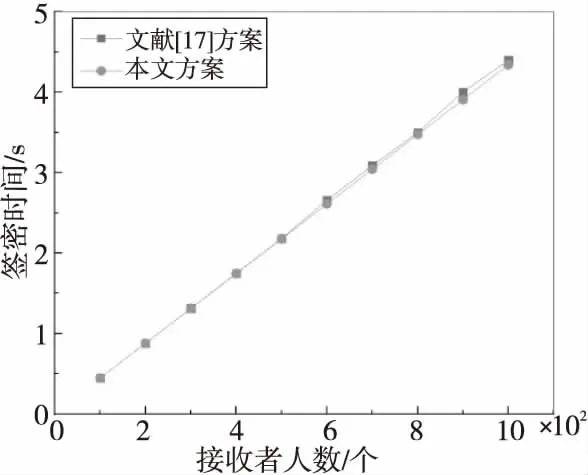
Figure 1 Signcryption time圖1 簽密時間

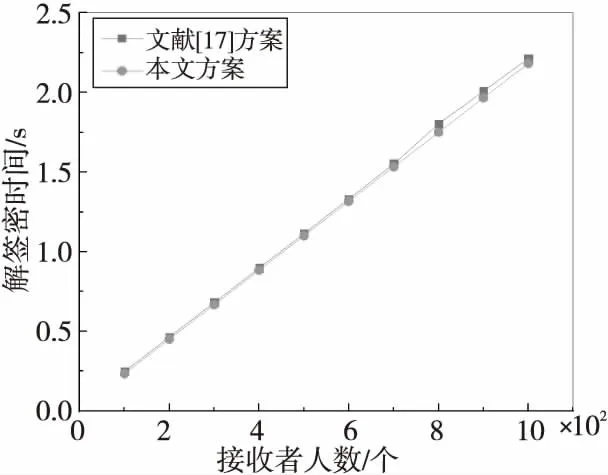
Figure 2 Unsigncryption time圖2 解簽密時間

6 結束語

異構密碼體制下能夠保證數據隱私的多接收方聚合簽密方案不但能在不一樣的密碼體制之間通信，同時還能保護發送方的隱私。本文分析了牛淑芬方案(文獻[17]方案)，指出該方案能夠被偽造，并設計了可證安全的隱私保護多接收者異構聚合簽密方案。改進的方案改善了原方案中的安全性不足，并滿足對多個消息聚合驗證的特點。下一步研究的重點是在保證數據隱私的同時提升計算效率。