基于SLP和粒子群算法的車間布局優化研究*

徐曉鳴，鄧裕琪，吳綺萍

（1.廣東海洋大學機械與動力工程學院，廣東湛江 524088；2.深圳市三一聯光智能設備股份有限公司，廣東深圳 518106）

0 引言

隨著全球經濟一體化進程加快，以及當前社會經濟存在下行風險，企業面臨提升核心競爭力的壓力與挑戰，合理的車間布局，能減少企業在制品庫存，提高空間利用率，降低生產成本[1]。因此，采用合理高效的車間布局方法對企業提高效率勢在必行。

車間設施布局問題實質上是一種組合優化問題，當布局的設備數量越多，求解越困難，至此國內外學者在該類問題求解進行了大量的研究。文獻[2]針對車間布局問題構建了各作業單位總物流強度最小和物流成本最小雙目標模型，并運用遺傳算法進行求解，并驗證了算法的有效性。文獻[3]結合傳統SLP方法，構建了物流總成本最小模型，并運用遺傳算法進行求解，驗證了算法的有效性。文獻[4]針對于車間布局問題構建了物流搬運總成本最小模型，并運用粒子群算法進行求解。文獻[5]構建了一個混合整數規劃模型，并運用切平面法進行求解，得出最優布局。上述文獻從不同的角度建立車間布局優化目標函數，然而從搬運物流成本最小和各作業單位間的非物流關系密切程度最大的多目標考慮不足。

本文在傳統SLP方法基礎上，構建了物料搬運成本最小和非物流關系密切程度最大目標規劃模型，借助粒子群算法對模型優化求解，結合實際情況對求得的結果進行調整，得出最優的布局方案。通過以SY公司為研究案例，對比前后布局方案的物料搬運成本和非物流關系密切程度，驗證方法的有效性。

1 車間布局問題建模

1.1 假設與參數

生產車間的設施布局問題是一個組合問題，各作業單位的面積尺寸不相同，車間的可利用面積有限，在建模時需要做以下假設：

（1）假設需要布局的設備結構均為矩形，長度和寬度均為可知，隨機擺放且平行于四周空間。

（2）各作業單位均為矩形，作業單位的長、寬尺寸和所需的面積均可求，各作業單位的中心點在同一水平線上。

（3）物料的運輸路線與車間的長度和寬度平行，且不考慮使用不同搬運工具產生的搬運不同費用，即單位搬運成本一致。

建模參數設計如下。

X為長度方向，Y為寬度方向，L為車間的總長，W為車間的總寬；Fi、Fj、Fk、FN為車間內第 i、j、k…N 個作業單位，共有N個作業單位；xj為作業單位Fj在X軸的中心坐標；yk為作業單位Fk在Y軸的中心坐標；li為作業單位Fi的長度；wi為作業單位Fi的寬度，m；dxik為作業單位Fi和作業單位Fk之間在X軸方向的最小距離，m；dyij為作業單位Fi和作業單位Fj之間在Y軸方向的最小距離，m；loj、woj分別為作業單位Fj距離Y軸和X軸的最小距離；dij為作業單位Fi和作業單位Fj的曼哈頓距離，m；cij為作業單位i到作業單位j之間的單位搬運成本，元/kg

·m；qij為作業單位i到作業單位j之間的年平均物流量，kg；dmax為生產車間總規劃區域的長與寬之和；Tij為作業單位i與作業單位j之間的非物流關系值，根據密切程度等級進行量化，如表1所示；bij為作業單位i與作業單位j之間的接近程度，稱為關系因子或關聯度，由dij轉化得到，如表2所示。

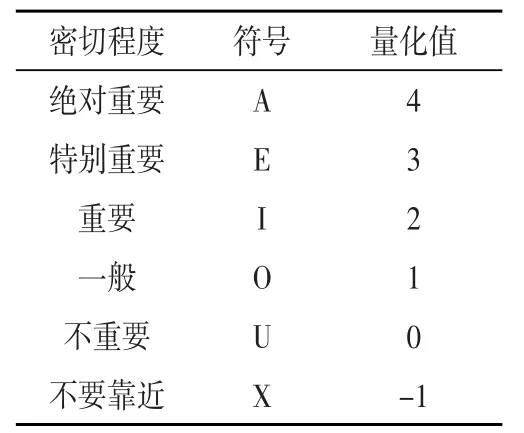
表1 作業單位間的密切程度量化表

表2 關系因子的確定

1.2 目標函數

車間設施布局以車間搬運成本（Z1）最低、作業單位間非物流關系密切程度（Z2）最大為車間布局模型的雙目標函數。

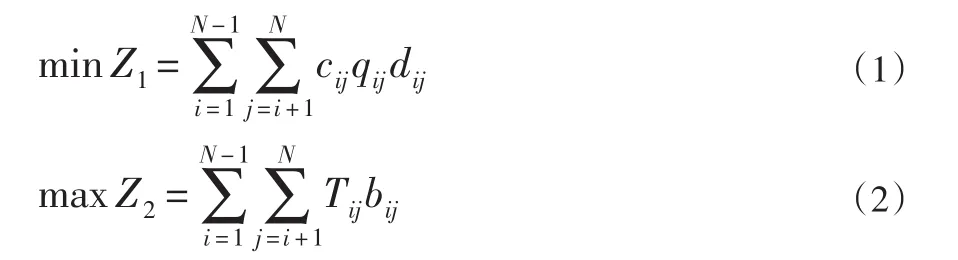
其中i和j為作業單位的編號，且i≠j。

將雙目標函數轉化為單一目標函數。

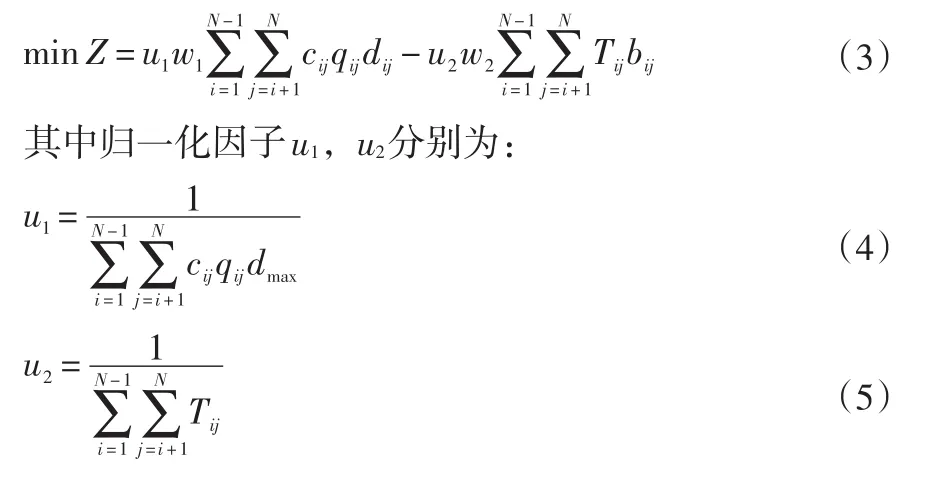
w1表示物料搬運成本的權重，w2表示非流關系密切程度的權重，且w1+w2=1。

1.3 約束條件

（1）間距約束

間距約束是指作業單位之間要留有適當的安全距離，作業單位不能重疊擺放。則間距約束可表示為：

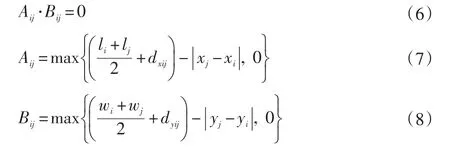
（2）邊界約束

車間的長和寬是一定的，各作業單位的總長和總寬應小于待布局車間的總長和總寬，且作業單位與車間的四壁應留有一定的距離。則邊界約束可表示為：

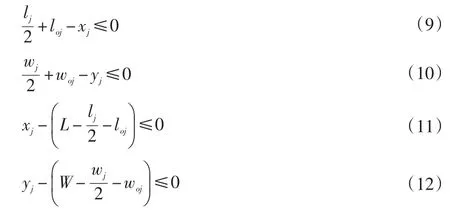
（3）固定約束

車間布局過程中，對一些特殊的設備和作業單位要單獨進行考慮，例如鍛造和電鍍等特殊單元一般都安排在角落，而有些作業單位的位置因為建筑結構等問題具有固定的位置，在布局時不能隨意變動，可以將這些比較特殊的作業單位區域固定下來，在布局設計時不在其中布置別的作業單位，設Dk為固定區域，則固定約束可以表示為：

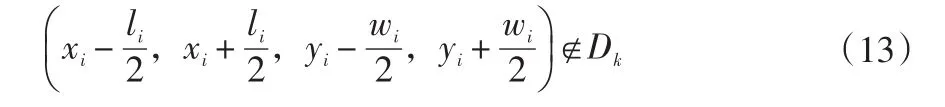
2 基于粒子群算法求解

2.1 編碼設計

假設待布局車間有N個待布局作業單位，每個車間布局方案對應為一個粒子，則每個粒子的位置和速度都為2N維向量。每個粒子的位置向量前N維標識作業單位坐標在X軸上的投影，后N個維標識作業單位坐標在Y軸上的投影；每個粒子的速度向量前N維標識在X軸上的投影，后N維標識在Y軸上的投影。具體的位置P和速度V在2N維度上的坐標如下式。

算法優化過程中主要通過追蹤Pbest和Gbest兩極值，在解空間中進行搜索，每個粒子按式（16）～（19）進行更新。

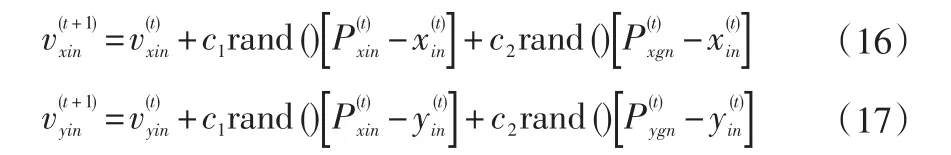
式中：t為迭代次數；c1、c2為非負常數，稱為加速系數；rand（）為均勻分布在（0，1）的隨機數；為第t次迭代時N維空間中的第i個粒子在X軸坐標上經過的最好位置；為第t次迭代時N維空間中的第i個粒子在Y軸坐標上經過的最好位置；為第t次迭代時N維空間中的粒子群在X軸坐標上經過的最好全局位置；為第t次迭代時N維空間中的粒子群在Y軸坐標上經過的最好全局位置；為下一輪迭代時，N維空間中的第i個粒子，在X軸上的投影；為下一輪迭代時，N維空間中的第i個粒子，在Y軸上的投影；n=（1，2，…，N），n表示N維空間中的第n個變量。

2.2 參數設計

（1）加速系數的確定

合理設置加速系數的取值，可以減少算法陷入局部極值中的概率，通常取c1=c2，且c1+c2≤4，根據經驗，一般取值在[0.5，2]之間能夠取得較好的優化結果。

（2）適應度函數

為保證適應度函數為非負，將目標函數做如下處理：

式中：Max為一足夠大的常數。

3 案例應用

3.1 案例概況

SY公司是一家專門從事SMD編帶機、貼片測試分類機、外觀檢測機等智能設備的生產，屬于中小型企業，按訂單組織生產。根據SY公司車間的生產設備狀況，結合輔助部門，按照功能相似性原則劃分出作業單位，劃分為12個區域，為別為：（1）來料存放區；（2）機加工區；（3）裝配區；（4）檢驗區；（5）物料存放區；（6）組裝區；（7）倉庫；（8）生產多料區；（9）IQC；（10）雜物間；（11）成品區；（12）滯銷設備存放區。

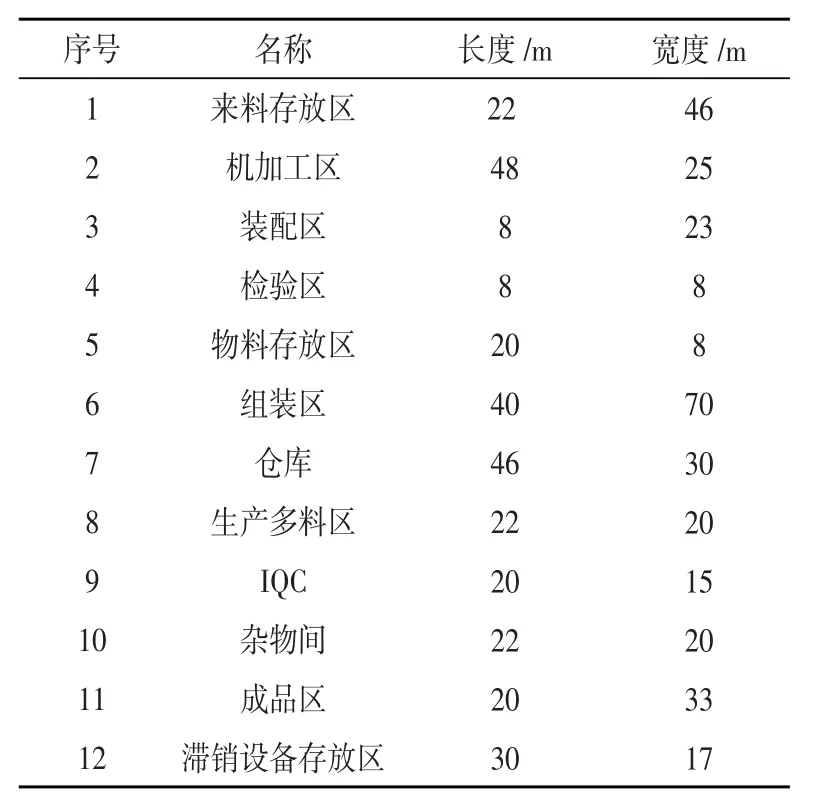
表3 作業單位面積設計值

擬布局的車間長175 m，寬120 m，各作業單位所占面積各作業單位所需面積如表3所示。

作業單位原坐標向量為：

X=[30 21.6 45 42 40 60 84 80 108 19 23 78]；

Y=[38 10 45 40 35 50 60 40 6 15 43 35]

3.2 物流分析

根據劃分的作業單位，對各作業單位間的年物料搬運量進行統計分析，得到各作業單位間的年物流量從至表，如表4所示。

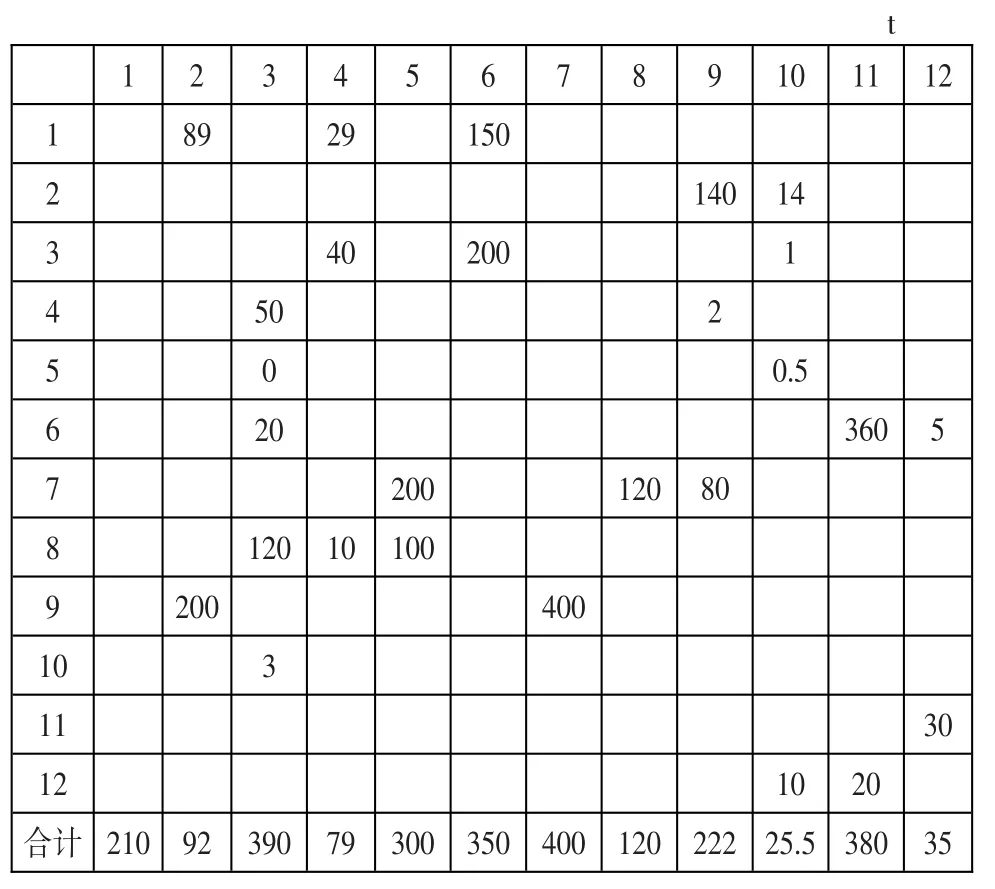
表4 作業單位間物流量從至表

3.3 非物流分析

根據SY公司設備生產的特點，制定各作業單位間相互密切程度理由，如表5所示。在此基礎上做非物流作業單位相互關系圖，如圖1所示。

表5 各作業單位關系密切程度理由

3.4 優化過程和參數設計

在本案例中，運輸成本c=0.01元/(kg·m)，dmax=295，Max=1 000，u1=1.3×10-7，u2=0.023 3。在實際中，SY公司沒有特殊的加工區域和需要固定的區域，因此不考慮固定約束。

為保證粒子群算法的優化效果，選取五種具有代表性的加速系數，分別運行1 000次，選取每種加速系數較優的3次結果進行對比。因為適應度值為目標函數的倒數，為使目標函數值最小，適應度值要選取最大的。不同的加速系數的對比分析如表6所示。

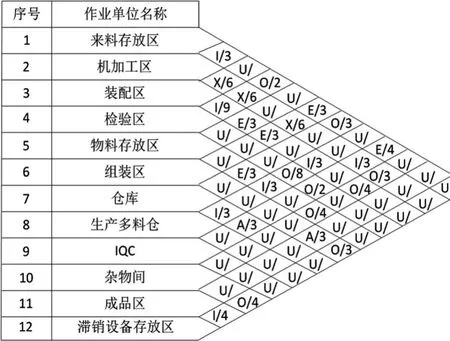
圖1 非物流作業單位相互關系圖

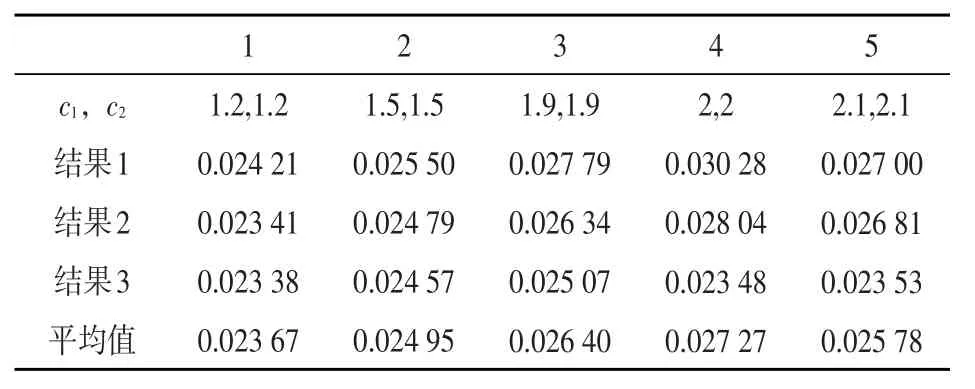
表6 加速系數對比分析

由表6可知，c1=c2=2時的適應度值平均值最大，即目標函數值最小，此時的優化結果為5個方案里的最優方案，運行求解過程如圖2所示。根據求解結果，獲得單個作業單位的坐標位置如表7所示。

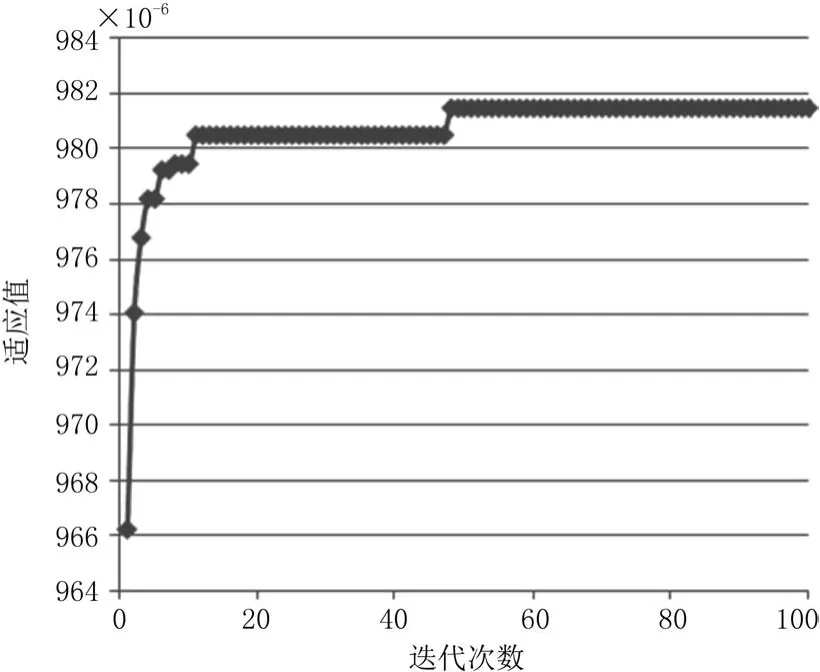
圖2 運行過程

理想狀態下的布局圖，考慮到實際布局的空間外形等限制條件，結合SY公司的車間建筑結構情況，對優化結果進行調整，得到最終的優化布局方案如圖3所示。

3.5 有效性分析

對SY公司生產車間原布局經過分析，給定作業單位原布局相應的坐標，代入算法中進行求解，再與優化后的值進行對比，優化前后方案對比如表8所示。

SY公司在改善前，物料搬運成本過高，導致產品的總體成本隨之升高，產品的市場競爭力相對較弱。通過布局改善后，降低了搬運成本，各作業單位之間的協作溝通也更加密切，生產管理就會更加順暢，因此，得出的優化方案有一定的可行性。

表7 X，Y坐標求解結果

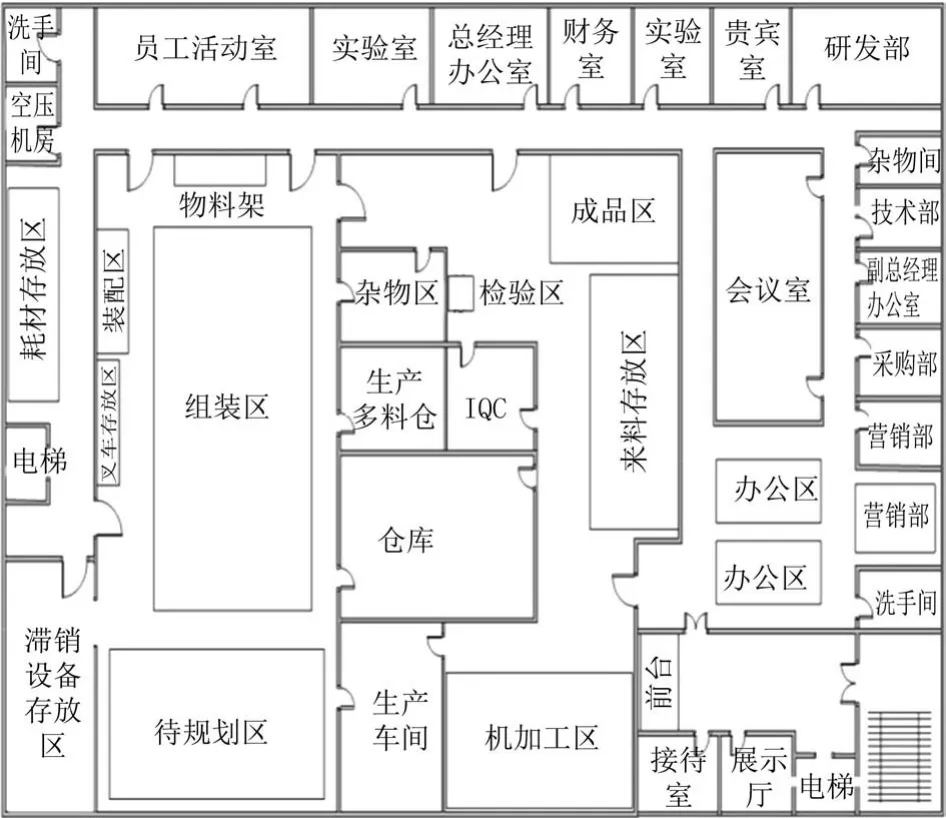
圖3 最終布局方案

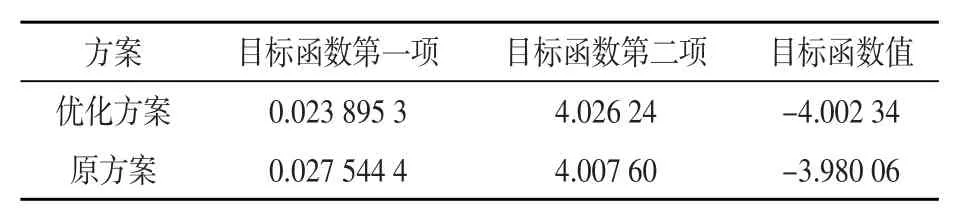
表8 方案對比分析

4 結束語

本文以SY公司的生產車間為例，對車間的現有布局進行了分析，找出現有布局問題的所在點。利用SLP方法進行車間布局的分析，對車間進行了作業單位的劃分，分析各作業單位間的物流量和非物流關系，對車間布局問題進行建模，以物流成本最小和非物流關系最大為雙目標進行分析求解，通過粒子群算法，最后得出優化的布局方案。通過優化前后布局方案的對比，驗證了優化后得車間布局方案可行，對SY公司車間布局改進具有一定的指導意義。

通過本文的研究與應用，運用SLP方法和粒子群算法能夠有效的解決企業布局問題，為相關企業解決布局問題提供了一種有效途徑。