自適應滑模摩擦補償在隔膜張力控制中的應用

王 韜，王恒升，周 君

（1.中南大學 機電工程學院，長沙410083；2.深圳市佳得設備有限公司，深圳518110）

隔膜是鋰電池的關鍵內層組件之一。 隔膜分切機是將大卷徑、寬幅的隔膜卷分切成小卷徑、窄幅的隔膜卷的設備，隔膜張力是決定產品質量最關鍵的因素。 在此以隔膜放卷張力控制為背景，在放卷過程中，隔膜卷的卷徑及慣量隨時間變化，加之摩擦、軸輥布局等其它不確定因素的影響，使得放卷系統成為一種集多輸入、多輸出、非線性、強干擾等為一體的復雜機電系統。 針對隔膜分切機在放卷過程中，由于負載慣量的時變性與摩擦的不確定性導致張力波動大的問題，提出了自適應滑模摩擦補償控制算法。

1 放卷軸動力學模型和摩擦模型

1.1 隔膜分切機放卷系統

隔膜分切機放卷系統的結構如圖1 所示。 在放卷過程中，非線性極強且時變的摩擦力矩總是存在的。 根據放卷輥的動力學模型和工程經驗有：為保證放卷張力穩定，需對放卷軸的摩擦進行實時補償。

圖1 隔膜分切機放卷系統Fig.1 Unwinding system of diaphragm slitter

為了減少摩擦對伺服運動系統的影響，學者們提出了多種控制和補償方案，基于摩擦力矩模型的前饋控制方案是最直接的方法之一。 文獻[1-2]對摩擦產生的機理進行了分析研究，提出了幾種摩擦建模方法，并對模型的實際應用進行了分析。 摩擦模型有靜態的和動態的，動態模型中最常用的是GMS模型和LuGre 模型。 文獻[3]對GMS 模型的機理和應用進行了詳細的描述。 針對摩擦模型的參數在系統運行時會動態變化，文獻[4-5]采用基于LuGre 模型的自適應控制對摩擦力矩進行前饋控制，滿足伺服運動系統的速度和位移跟蹤精度。

對于負載慣量時變和摩擦不確定的問題，在此提出基于LuGre 模型的自適應滑模ASM 控制補償算法。時變參數的自適應律由Lyapunov 函數推導得到， 為了防止時變參數出現過大甚至為負的現象，在此引入了自適應映射算法。

1.2 放卷軸動力學模型

在圖1 中， 輥1 為伺服電機驅動的放卷輥，采用力矩控制模式；r1為套于輥1 的鋰電池隔膜卷內徑；R1為隔膜卷外徑；輥2 為張力傳感器輥，用于測量放卷隔膜張力； 輥3 為電機驅動的主速度輥，采用速度控制模式，產生隔膜傳送基準速度。 由牛頓第二運動定律，放卷軸放卷時的動力學方程為

式中：J 為放卷軸的總轉動慣量；ω 為放卷電機角速度；η 為傳動機構傳動效率；j 為傳動比；u 為電機力矩；T 為放卷張力；R 為隔膜卷外徑；Tf為放卷機構中的摩擦力矩；Δ（t）為包括外界干擾和模型不確定部分的總的不確定性，且設不確定性Δ 有界，可表示為

由文獻[7]可知，在放卷的單位時間內有

式中：h 為隔膜厚度；v 為放卷軸的線速度。

聯立式（1）（3），得

由于h 為μm 級，為便于計算，可略去式（4）最終結果的第2 項，簡化后放卷軸在放卷時的動力學方程為

而放卷軸單獨轉動（即空載）時的動力學方程為

比較式（5）（6）可知，放卷軸放卷與空載的區別是有、無隔膜張力力矩的影響。 在此擬通過放卷輥的速度跟蹤試驗來驗證摩擦補償算法的有效性，并將該算法應用于隔膜放卷張力控制中，以提高張力控制精度。

1.3 摩擦模型及特性分析

對于式（6）中的Tf，采用廣泛使用的動態模型——LuGre 模型，其表達式為

式中：z 為2 個接觸面之間鬃毛的物理偏移量；ω 為角速度；σ0，σ1，B 分別為鬃毛剛性系數、阻尼系數和黏滯摩擦系數；Fc為庫倫摩擦矩；Fs為靜摩擦矩，且Fs>Fc；ωs為斯特里貝克速度。 根據ω 和ωs的大小，將摩擦分為2 種狀態——黏附狀態 （當|ω|<ωs）和滑動狀態（當|ω|>ωs）。

由摩擦特性可知，當ω 較大，即純滑動摩擦狀態時，dz/dt≈0；當ω 較小且換向時，即在黏附狀態時，dz/dt 存在較大值。 因此對于純滑動摩擦狀態，依據式（7），有

根據式（7）（8），滑動狀態時，基于LuGre 模型的摩擦力矩為

通常ωs都非常小，根據指數函數的性質，當ω較大時，式（9）右邊的第2 項近似為零。 因此，滑動狀態時LuGre 模型可近似為

2 自適應滑模摩擦補償方案

2.1 補償控制器的設計

根據張力的產生原理，放卷張力控制的本質即對放卷軸進行目標速度跟蹤控制。 為此定義角度誤差eθ和轉速誤差eω分別為

定義跟蹤誤差的線性滑模面為

式中：θd為給定角位置；θ 為實際角位置；ωd為給定

角速度；ω 為實際角速度；c>0。

實際工程中，可以將S 控制在一定范圍δ 內。在此引入一個新的滑模面SΔ，定義為

其中

式中：sat（x）為飽和函數。 SΔ具有以下性質：

由SΔ的結構和定義可知δ 的大小直接決定了控制器的精度。

由式（6），得到放卷電機的驅動力矩為

因式中的J 和Tf不確定，由式（15）計算出的驅動力矩不能達到設計的速度要求。 為此，基于滑模控制策略所設計的控制律為

在理想情況下，當SΔ=0，此時由式（16）估計的慣量和摩擦力矩就應該是其真實值。 由式（16）得到控制系統的結構如圖2 所示。

圖2 自適應滑模摩擦補償控制系統框圖Fig.2 Block diagram of ASM friction compensation control system

2.2 系統穩定性分析

將控制律（16）和式（10）代入式（6），有

其中

令

定義的Lyapunov 函數為

其中

式中：η1，η，η3為正增益。對式（19）求導，將式（17）代入，可得：

由式（20），可得J，Fc，B 的自適應律為

將自適應律（21）代入式（20），有

式中：ε，β 均為正常數，且ε>D。 綜合符號函數的性質為

故

其中投影映射算法，Projξ（·）定義如下：

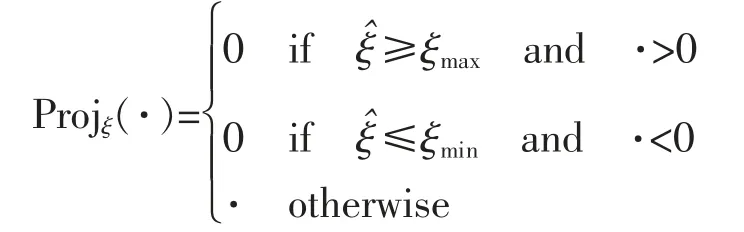
至此設計完成ASM 摩擦補償控制器。

3 仿真

3.1 仿真設置

為驗證所提出ASM 控制器能夠正確估計出模型參數，并能夠實現速度跟蹤，在此進行了仿真。

單軸驅動的仿真采用式（6）給出的模型。 其中，伺服電機的力矩環假定為理想，即其傳遞函數為1；無擾動影響，仿真步長為0.0001 s；模型參數為J=0.0156，Fc=0.32，B=0.025，均取國際單位制。

轉速給定設置為變加速曲線，即10+2sin（t），單位為rad/s；給定位置和給定加速度可以通過對給定速度進行積分和微分運算得到。

ASM 控制器的參數通過仿真調試，設定為c=5，β=10，ε=0.12，δ=0.01，η1=5，η2=20，η3=10。

需要在線估計的參數初值均設置為0。

3.2 仿真結果

仿真結果如圖3 和圖4 所示。 由圖可見，轉動慣量約在0.005 s 就收斂于真值，摩擦矩約在0.6 s達到其真值，系統很快正確地辨識出模型參數。

圖3 模型參數估計曲線Fig.3 Model parameter estimation curve

圖4 ASM 控制跟蹤誤差Fig.4 Tracking error of ASM control

圖4 為控制系統的轉速、角位移的誤差曲線，在模型參數估計值收斂后（約0.6 s），誤差曲線趨近于0。

4 試驗驗證

試驗分切機包括放卷軸和主驅動軸，采用被動式的表面收卷方式。試驗分切機實物如圖5 所示。2個驅動軸分別由倍福的伺服電機AM-8042 和AM8052 驅動， 控制器采用倍福的CX-3E80AE 型PLC。 程序掃描周期為1 ms。

圖5 試驗分切機實物Fig.5 Experimental slitting machine

4.1 速度跟蹤試驗

在ASM 控制器的速度跟蹤試驗中，對放卷電機用力矩控制模式。 設置

式中：ωd為目標轉速，（°）/s。

ASM控制器的參數選取為c=20，β=0.15，ε=0.05，δ=3，η1=3×10-8，η2=2×10-5，η3=1.5×10-6。

為了降低系統的不確定性，放卷機構的轉動慣量使用放卷恒速試驗計算出的真實值為0.0125 kg·m2；為了加快系統的收斂，使用曲線擬合的方法識別出摩擦參數的初值，并將其估計值限定在給定區間內，其中Fc初值為0.2605 NM∈［0.2581，0.2635］，B 的初值為0.006842∈［0.006593，0.007091］。 該試驗原理在此不再贅述。

試驗結果分析如下：

設置的目標轉速與實際轉速如圖6 所示，發現ASM 控制能滿足對目標轉速跟蹤的要求。 其中，超調量約為25%；調節時間約為4 s。這表明ASM 控制器的動態響應快速、平穩。

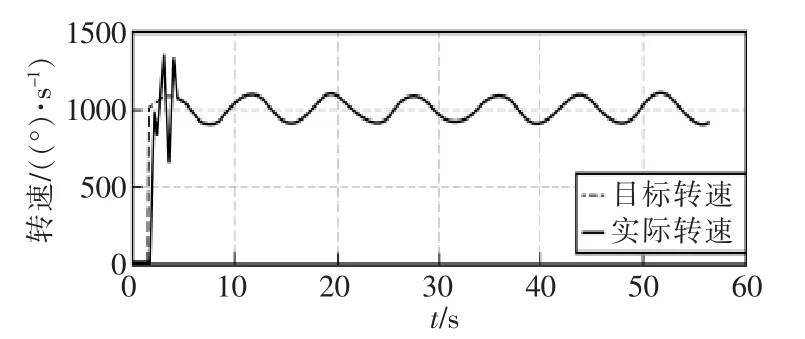
圖6 ASM 控制和PD 控制下的速度跟蹤情況Fig.6 Angular velocity tracking under ASM control and PD control

ASM 控制的角位移誤差、 速度誤差曲線如圖7，8 所示。 由圖7 可見，速度誤差的均值為0，速度誤差的穩態誤差為±0.3 rad/s，其中系統的固定誤差為±0.2 rad/s。 由圖8 可見，ASM 控制的角位移穩態誤差為±0.015 rad。 這表明ASM 控制器的穩態誤差小、精度高。

圖7 仿真轉速誤差Fig.7 Velocity error of simulation

圖8 仿真角位移誤差Fig.8 Position error of simulation

在使用ASM 控制下的速度跟蹤試驗中，通過自適應律識別出的時變摩擦參數Fc和B 的變化曲線如圖9 所示。

速度跟蹤試驗驗證了所提出的ASM 控制器的控制性能和精度均能滿足控制目標，同時也驗證了該算法能快速識別變化的摩擦力矩，并進行有效地補償。

圖9 摩擦參數估計值Fig.9 Estimations of friction parameters

4.2 張力控制試驗

在隔膜放卷試驗中，對PID+ASM 摩擦補償和PID+靜態摩擦補償，這2 種摩擦補償策略在分切機變速和勻速情況下放卷張力的控制效果進行了比較。隔膜放卷張力控制如圖10 所示。試驗所用參數見表1。

圖10 PID+摩擦補償張力控制系統框圖Fig.10 Block diagram of PID+ASM tension control system

表1 張力控制試驗用參數Tab.1 Parameters for tension control test

PID 控制器參數為KP=0.12，KI=0.1，KD=0.05。

在該試驗中，分別測試了2 種摩擦補償方案在相同期望張力Tset=4 N， 變速情況下放卷隔膜張力的控制效果，試驗結果如圖11，12 所示。

通過對試驗結果進行分析可知，在分切機變速和勻速的整個運動過程中，采用ASM 摩擦補償的張力控制效果都更為理想，其跟蹤誤差更小，約為±0.7 N，而采用靜態摩擦補償的跟蹤誤差約為±1.5 N； 而且前者在變速過程中的控制性能也更好，加減速過程中其張力波動很小，而后者的張力波動卻很明顯。

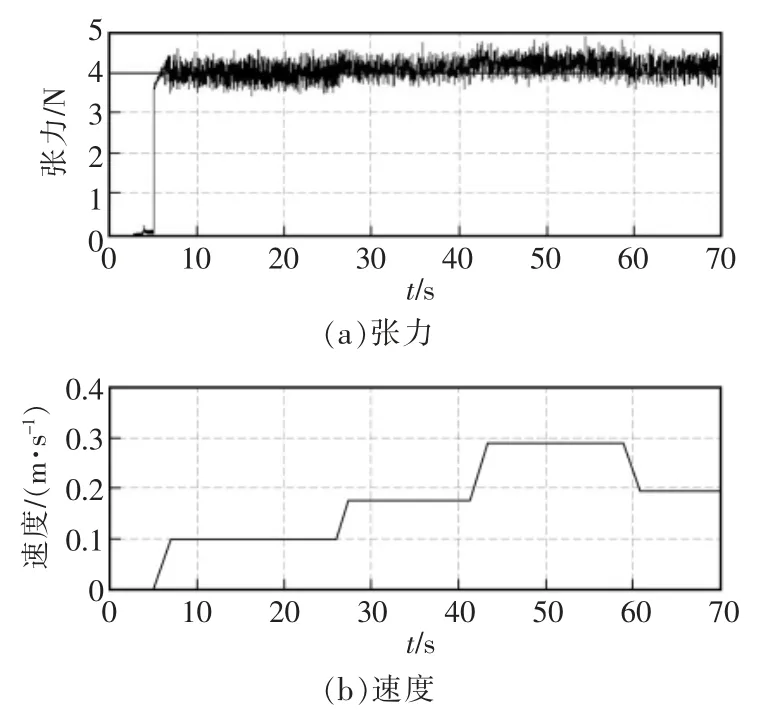
圖11 PID+ASM 摩擦補償的張力控制效果Fig.11 Tension under PID+ASM friction compensation

圖12 PID+靜態摩擦補償的張力控制效果Fig.12 Tension under PID+Stati friction compensation

綜合上述跟蹤對比試驗和放卷張力控制試驗可知，所設計的ASM 摩擦補償方案能有效地對變化的摩擦進行補償，能明顯提高隔膜張力控制精度。

5 結語

針對放卷機構中存在變化的摩擦力矩進而造成隔膜張力波動的現象，根據放卷軸的動力學模型和LuGre 摩擦模型，圍繞摩擦力矩補償問題提出了ASM 摩擦補償方案。 采用Lyapunov 穩定性理論推導得出摩擦參數的自適應律，并進行了穩定性證明。為了防止時變參數過大或為負，根據實際情況對時變參數進行映射自適應算法修正。 仿真和試驗都表明，所設計的ASM 摩擦補償方案能實現摩擦力矩的有效補償， 并且能顯著地提高隔膜分切機的張力控制精度和穩定性。