基于三次樣條插值法的干涉儀反射鏡面型值誤差分析

李 峰，汪杰君，熊顯名，張文濤，杜 浩

（桂林電子科技大學 電子工程與自動化學院，廣西 桂林 541004）

0 引言

集成電路產業是信息技術產業的核心，是支撐經濟社會發展和保障國家安全的戰略性、基礎性和先導性產業，當前和今后一段時期是中國集成電路產業發展的重要戰略機遇期和攻堅期[1]。光刻機，被譽為人類20世紀的發明奇跡之一，是集成電路產業皇冠上的明珠，研發的技術門檻和資金門檻非常高[2]。對于集成電路產業來說，高端制造是進行集成電路生產的基礎。作為“國之重器”的高端光刻機，其研制是國家戰略需求，國家科技重大專項“極大規模集成電路制造裝備及成套工藝”明確將28nm浸沒式光刻機產品作為專項的標志性目標成果。在光刻機的研究中，套刻精度一直是光刻機的重點和難點，而光刻機的測量系統則是關系到光刻機精度的重要環節。

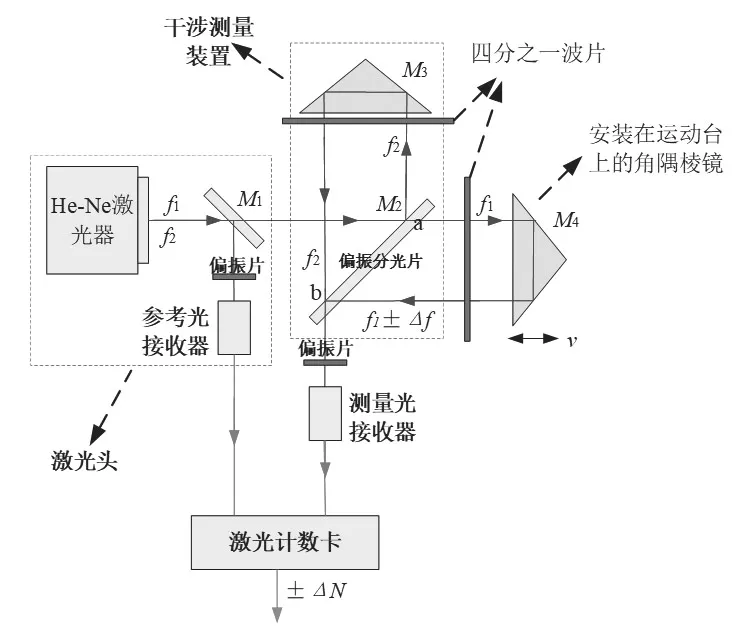
圖1 激光干涉儀測量原理圖Fig.1 Measurement schematic diagram of laser interferometer

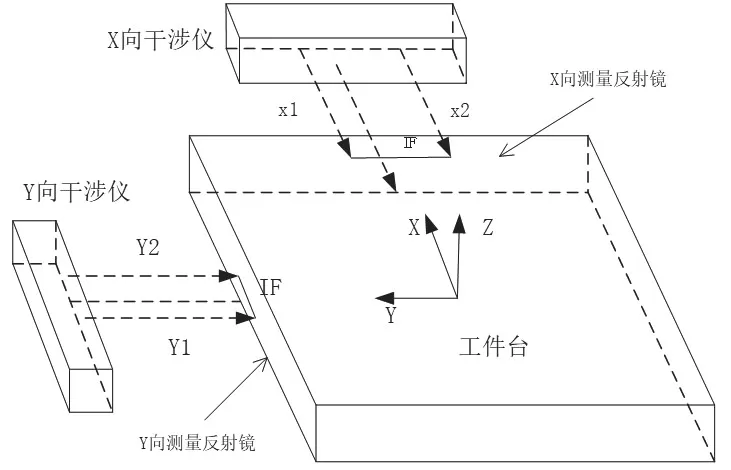
圖2 運動臺干涉儀測量系統結構Fig.2 Structure of interferometer measurement system

光刻機的運動臺位移系統使用的是雙頻激光干涉儀進行測量位移[3]。雙頻激光干涉儀總體由兩部分構成：光學系統和電路系統。光路系統由氦氖激光器、擴束鏡、檢偏器、光電接收元件、干涉鏡等組成。雙頻激光干涉光路系統后續信號處理包括光電轉換、放大整形、電子細分、連續計數、單片機和數碼管顯示等[4]。激光干涉儀測量系統的精度受多種因素影響，其測量誤差主要包括：①系統誤差，主要指受到激光干涉測量方法及測量系統元部件制造精度的限制；②阿貝、余弦誤差，在測量系統安裝過程中，測量軸線與被測對象的運動軸線之間的誤差角以及測量過程中被測對象多自由度運動等形成的誤差；③環境誤差，干涉儀工作過程中，環境的波動（空氣溫度、壓力及相對濕度的變化）引起空氣折射率的變化，由此導致的誤差；④延時誤差，由干涉儀測量電路延時、測量數據滯后所產生的誤差[5]。本文對系統誤差進行了研究，主要是研究干涉儀中平面鏡面型由于加工制造的缺陷產生的誤差，根據激光干涉儀的測量原理，利用三次樣條抽樣法對干涉儀反射鏡面型進行了仿真，最后算出了激光干涉儀反射鏡面型值的誤差。

1 激光干涉儀測量位移原理概述

1.1 激光干涉儀測量位移原理

激光干涉儀測量原理如圖1所示。激光干涉儀測量系統包括：激光頭（亥氖激光器、參考光接收器、偏振片、偏振分光器）、干涉測量裝置（角隅棱鏡、偏振分光片）、測量光接收器和激光計數卡。

激光器輸出頻差穩定的雙頻激光經過分光片M1分光，一束作為參考信號經過偏振片后變成頻率為f2-f1的光直接由參考光接收器接收，另一束光則經過干涉測量裝置中的偏振分光片M2后在a點分離成頻率為f1和f2的光，頻率為f2的光經過角隅棱鏡M3的全反射，回到偏振分光鏡的b點處；頻率為f2的光經過四分之一波片后射入安裝在運動臺上的角隅棱鏡，當運動臺發生移動時，根據多普勒效應，由角隅棱鏡返回的光的頻率變為f1±△f，該光束與頻率為f2的光在偏振分光片M2的b點處匯合，匯合后的光經過偏振片后變成頻率為f2-f1±△f的測量光。根據干涉原理，參考光與測量光過激光計數卡的處理，即可計算出運動臺的位移△L。

激光干涉儀的基本公式為：

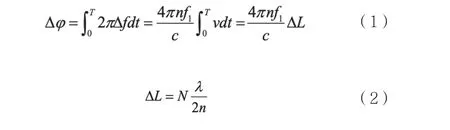
其中，N=Δφ/2π，Δφ表示相位差，λ表示波長。

1.2 干涉儀測量位移系統

根據干涉儀測量位移原理，運動臺干涉儀測量系統結構如圖2所示，其中的干涉儀采用的都是雙軸激光干涉儀。X向干涉儀的測量光束X1和X2與X向測量反射鏡垂直，與運動臺坐標系中的X軸平行；Y向干涉儀的測量光束Y1和Y2與Y向測量反射鏡垂直，與運動臺坐標系中的Y軸平行。Y向干涉儀的兩條測量光束的測量值y1和y2可以計算出運動臺的Y向位移y：Y=(y1+y2)/2，同時也可以測量出工件臺繞Z軸的旋轉度ΦYZ：ΦYZ=(y1-y2)/IF，IF表示雙軸干涉儀中兩測量光束之間的間距。同理，X向干涉儀可以測量出運動臺X向的位移x：X=(x1+x2)/2，運動臺繞Z軸的旋轉度

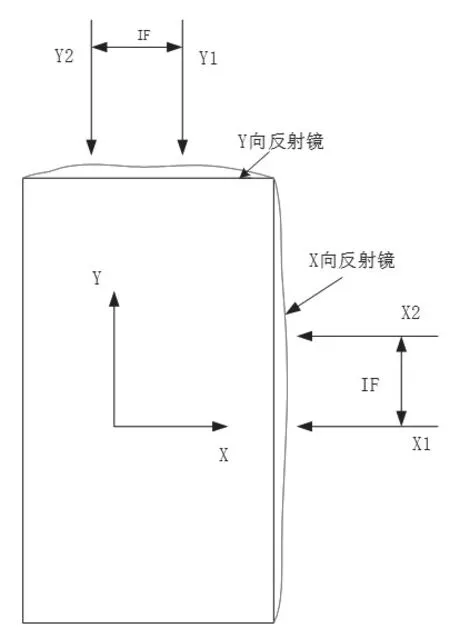
圖3 干涉儀反射鏡實際面型Fig.3 Actual map of interferometer reflector

2 干涉儀反射鏡面型校準

2.1 面型校準的原因

干涉儀的反射鏡由于加工、裝配精度、所受應力以及環境等因素的影響，其表面面形不可避免會存在一定的缺陷，即實際面形與理想面形存在一定的偏差，如圖3所示。由于運動臺定位控制時依賴于干涉儀的讀數，從圖中可以看出，若存在反射鏡面形，會導致包括X、Y兩個方向和Rz方向的測量值和臺子的真實值不一致，導致運動臺的定位出現誤差，所以需要對干涉儀反射鏡的面型進行測量校正以補償測量誤差。X向測量反射鏡的位置x的不平整度的校正值YMX，旋轉度ΦXZ修正值YΦZ；Y向測量反射鏡的位置y的不平整度的校正值XMY，旋轉度ΦYZ修正值XΦZ。

2.2 反射鏡面型計算方法

如圖4所示，首先由X向干涉儀控制ΦXZ保持不變（設置為零），由Y向干涉儀控制工件臺在Y方向保持零位，工件臺在X軸方向進行往返運動，讓Y向干涉儀能讀取到整個Y向反射鏡的面形讀數，如此可以測量得到在不同X位置處的面型值XΦZ的值。工件臺在最左端時如圖中綠色圖形所示，在右端時如圖中紅色圖形所示。干涉儀X向反射鏡面型向校準方法同Y向反射鏡面型校正方法一樣。

平移面形的計算基于旋轉面形，涉及到局部面形結構，干涉儀光束和局部面形之間的結構示意圖如圖5所示。在干涉儀光束Y1測量j點的同時，Y2測量了j+1的點面形值，它們之間的間隔為IF。同時，基于之前的旋轉面形XΦZ，可以得到j點處的旋轉面形值Mj。由圖中的幾何關系可得到Y向不同X處的面型值為：

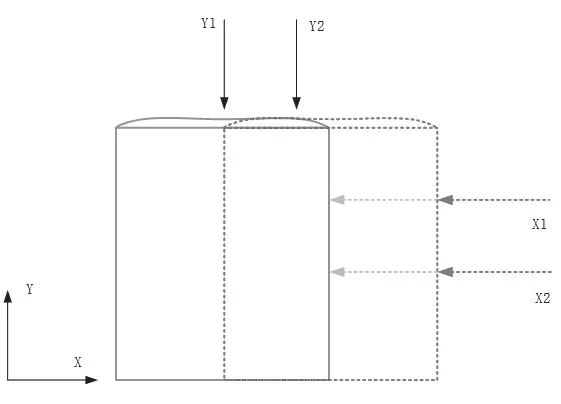
圖4 反射鏡面型計算原理Fig.4 Calculation principle of interferometer reflector

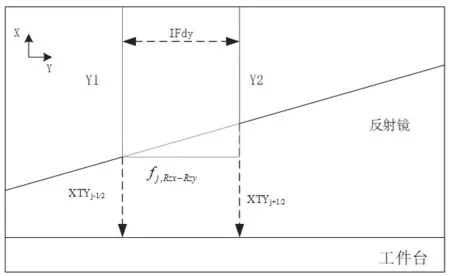
圖5 干涉儀光束之間結構示意圖Fig.5 Schematic diagram of interferometer beam structure

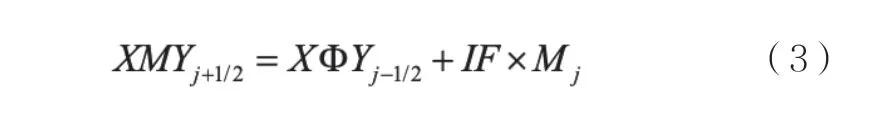
2.3 公式推導

工件臺在X=0處沿Y向運動，根據第i個測量點的旋轉偏移量Mi，可得該點的旋轉面形，具體推導過程如下：

如圖5所示，定義函數M(y)是描述X反射鏡在y位置處關于面形的連續函數，x1mea(y)和x2mea(y)為在不同的Y向位置干涉儀光束實際測量的值，那么X向干涉儀測量得到的真實值分別為：

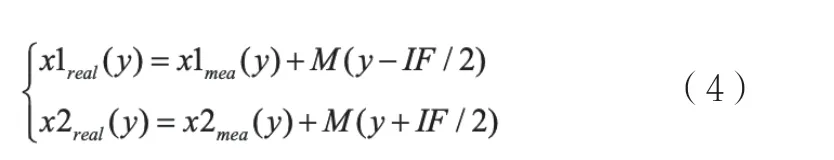
而工件臺位置和旋轉的真實值如下：

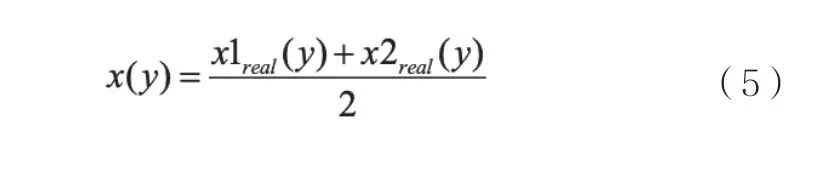
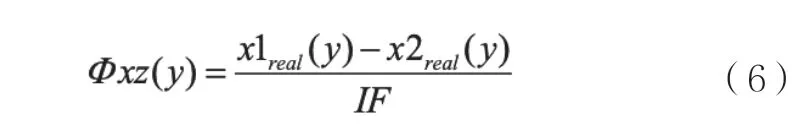
由此可以得到：

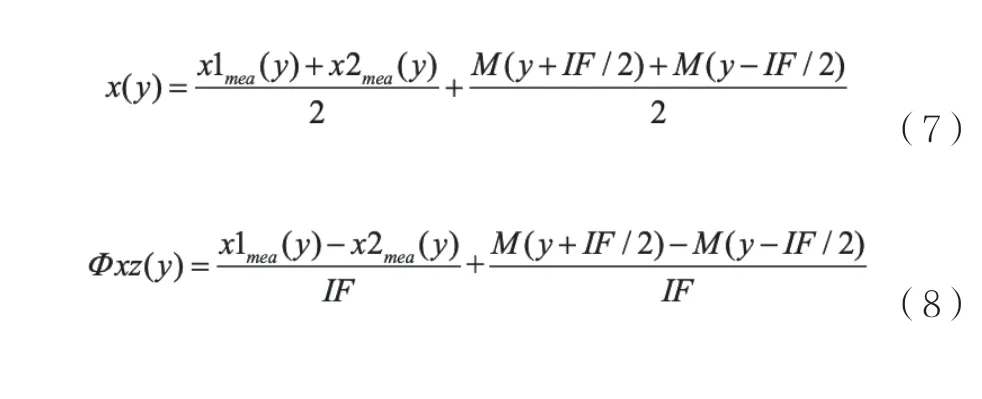
真實的測量位置x和旋轉ΦXZ為未校正的測量結果與面形校正值之和，即：

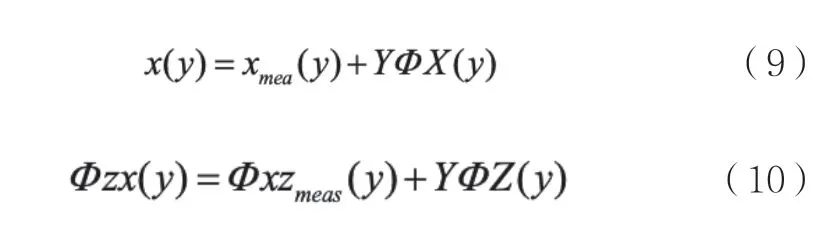
其中有：

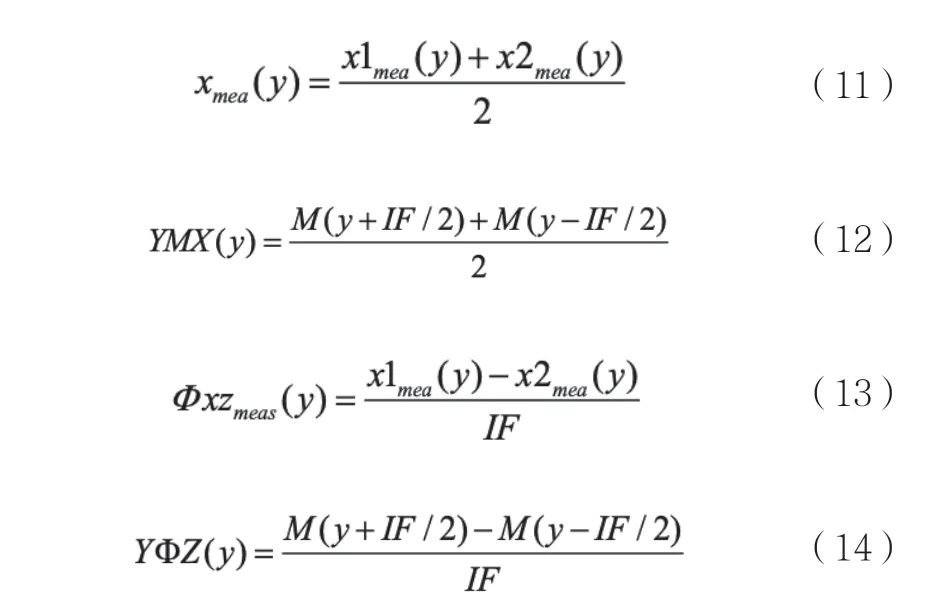
3 仿真實驗與分析

3.1 三次樣條插值算法

對于一組離散的數據yi=y(xi)，i=1,2,3...N，其三次樣條曲線S(x)滿足如下條件：

1）S(x)是分段曲線，在每一個分段區間內部[xi，xi+1]，S(x)=Si(x)是一個三次曲線。

2）在每一個xi處，S(xi)=yi

3）S(x)的一階導數S'(x)和二階導數S"(x)在整個區間[x1，xN]內連續；則對每一個區間內的樣條曲線的分段函數可以表述為：

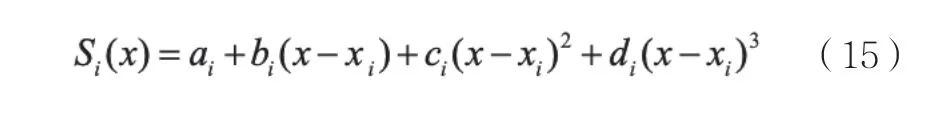
其中，ai，bi，ci，di代表4N個待求系數，由前述3個條件可得如下表達式：

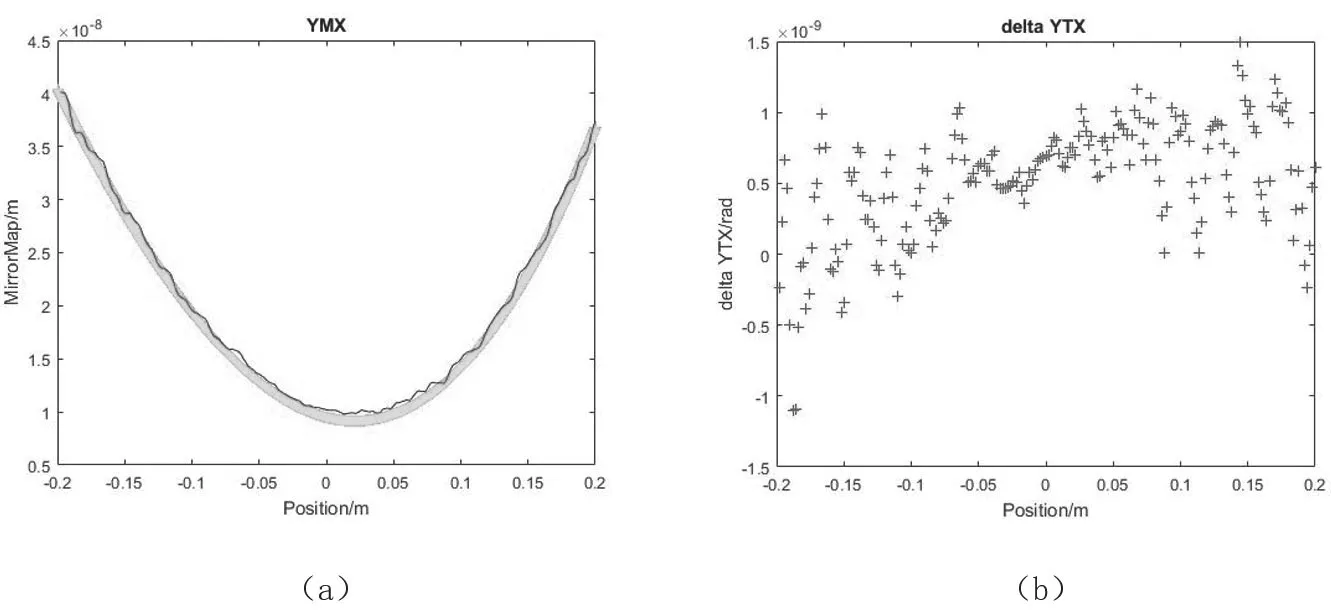
圖6 YMX的仿真結果Fig.6 Simulation result of YMX

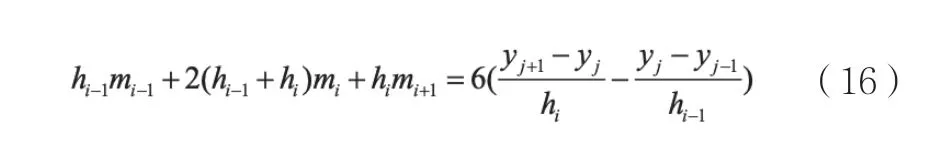
其中：

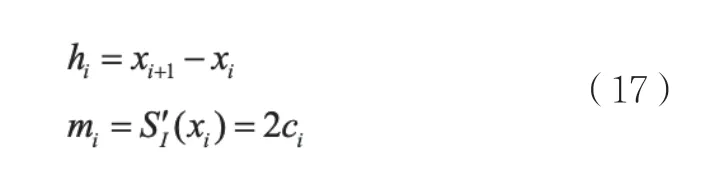
可將上述方程寫成矩陣的形式：

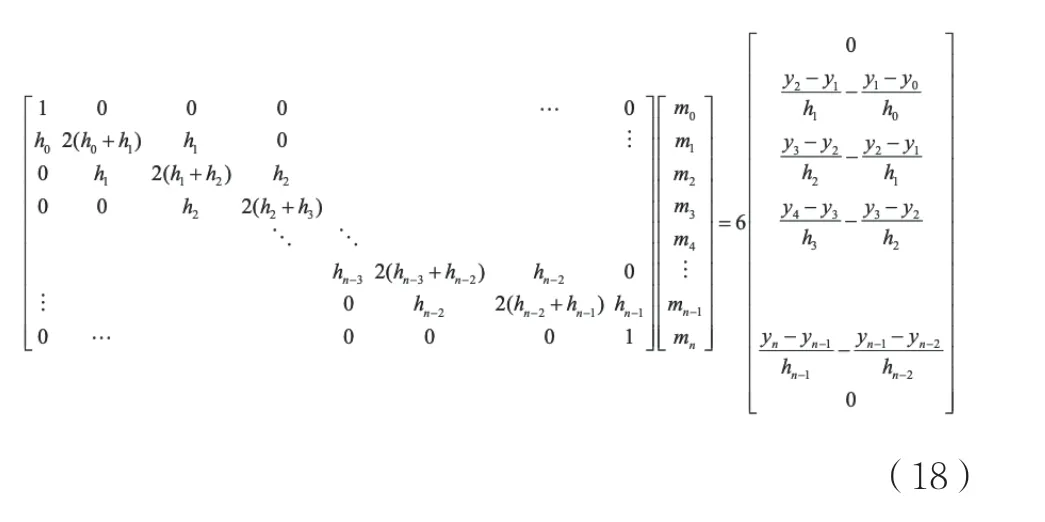
限定邊界條件為m0=0和mn=0。

對于如上矩陣，根據三角矩陣的解法，直接可得：

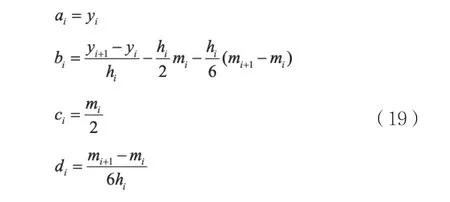
3.2 模型仿真

如圖6所示，為本文設計的模型仿真的結果圖，主要是針對X向反射鏡面型的仿真，使用的軟件是Matlab R2015b。首先，設置了一個模擬真實面型的函數M(y)，然后模擬了運動臺的Y向運動軌跡，根據運動軌跡進行測量點的數據采集，根據公式可以模擬出工件臺位置，然后利用三次樣條插值算法對這些數據進行處理，最終可以模擬出測量到的面型值。

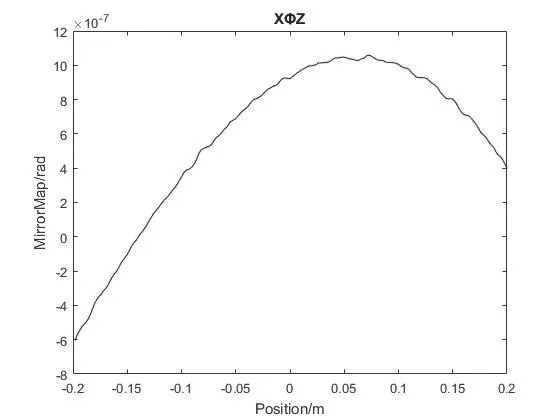
圖7 XΦZ的仿真結果Fig.7 Simulation result of XΦZ

如圖6（a）所示，綠色粗線為設置的模擬真實面型的函數 M(y)，而藍色細線為用三次樣條插值算法處理后得到的面形值YMX，是模擬測量的面形值。可以從中看出，測量值的面型YMX基本與設計出的真實面型值函數相擬合。圖6（b）是測量的面型值的誤差。本文模擬的X向的行程為±0.2m，重復測量了5次，可以從中看出面型最大的誤差在1.68×10-10m，而且越靠近量程的中心處，誤差就會越小。

圖7是旋轉面型XΦZ的仿真結果。可以計算出XΦZ最大的誤差是1.06×10-6rad，基本在快靠近程的中心處取得最大的補償量，計算出XΦZ的標準差為7.49×10-7rad。

綜上分析，本文設計的干涉儀反射鏡面型校準方法可以有效地算出干涉儀的面型值，而且算出的面型值與實際的面型值的擬合度較高，YMX最大的誤差在1.68×10-10m左右；XΦZ最大誤差的值是1.06×10-6rad，標準差為7.49×10-7rad，該校準方法滿足相應的技術指標。

4 結束語

本文設計了激光干涉儀測量位移系統反射鏡的面型值計算方法。通過對激光干涉儀位移測量系統的測量原理的分析，設計出了對干涉儀反射鏡面型值計算方法，并通過MATLAB仿真計算出了該方法測量X向反射鏡在±0.2m量程的YMX面形值的最大誤差為1.68×10-10m，XΦZ最大誤差的值是1.06×10-6rad，該方法可以為實際的工程設計提供參考價值。