基于力電耦合效應的非均勻壓電材料斷裂問題研究
朱帥 劉海濤
摘要 作為一種智能材料,非均勻壓電材料廣泛應用于航空航天、軍事等領域,由于其脆性,材料中的微裂紋對結構壽命影響較大。基于非均勻壓電材料的本構關系,幾何關系和邊界條件,利用分層法的原理進行材料的梯度劃分,分析了力電耦合效應下非均勻壓電材料中的斷裂問題。建立含裂紋非均勻壓電板的有限元模型,討論了力電耦合效應下不同梯度參數、不同裂紋形狀、不同裂紋尺寸以及不同梯度函數對裂紋周圍應力和電位移分布的變化規律。首次提出幾何過程函數來進行非均勻材料屬性的調控,實現材料參數的隨機遞增/隨機遞減。數值結果給出了在力電耦合效應下,裂紋周圍應力和電位移的分布規律;梯度參數的增大使裂紋周圍應力和電位移增大;裂紋幾何尺寸變小,裂紋周圍應力增大而電位移減小且橢圓形裂紋周圍應力要大于圓形裂紋。因此,在非均勻材料結構設計中,梯度參數應在可使用范圍內選取較小值;選擇不同梯度函數的對裂紋周圍的應力和電位移有一定影響,這對于非均勻壓電材料結構設計及實際應用起到借鑒作用。
關 鍵 詞 非均勻壓電材料;分層法;梯度函數;力電耦合效應;斷裂力學
中圖分類號 TB34 ? ? 文獻標志碼 A
0 引言
目前,壓電材料是智能結構系統中研究最多的傳感驅動材料[1],具有廣泛的應用前景。壓電材料受到機械應力會產生電場,而通過外加電場可以使壓電結構產生應力,因而具有良好的力電耦合特性,被應用于航天航空、軍工、人工智能等領域。非均勻材料是一種通過連續改變其組成物質比例,使其界面成分和組織實現連續過渡變化的梯度材料,通過梯度函數的調控,使材料的力學特性沿著一個方向呈連續變化,如彈性模量都是以函數的形式實現梯度的過渡。由于壓電材料在制造和使用過程中會發生疲勞斷裂或者產生微孔洞,使材料發生破壞,進而導致結構失效。當非均勻材料與壓電材料的結合時,可以使壓電材料的內部應力大為緩和,整體改善材料結構,不易發生破壞,大大提高材料的可靠性和使用壽命。因此,研究非均勻壓電材料板的斷裂問題對于提升相關結構器件的性能具有重要意義。
對于非均勻壓電材料的研究,只有特定的情況下可以給出解析解,當邊界條件變化以后,求解就變得相當困難。當前大部分工作基于簡單的邊界條件,給出了非均勻壓電梁板結構的基本解。Nguyen等[2]利用間斷伽遼金法計算高階連續體,降低了對位移連續性的要求。Elouafi等[3]基于Mori-Tanaka等效方法和Eshelby張量給出了非均質壓電材料等效參數的解析解。崔世堂等[4]利用TTO模型確定了材料的力學參數,研究了功能梯度梁的矩形截面在純彎曲荷載下的應力分布和彈塑性邊界演化規律。韓旭等[5]利用Fourier變換研究了層合壓電材料力電耦合在外載下的瞬態響應。Nourmohammadi等[6]對非均勻壓電材料的多場耦合問題進行了研究。張豐等[7]以菱壓電作動器為隔振器件,在力電耦合場下,研究了隔振系統的誤差、遲滯等多種工況下的數值仿真分析結果。Selimb等[8]利用高階剪切變形理論對功能梯度壓電板的振動問題進行了分析。張瑩等[9]利用England-Spencer理論獲得了圓板和圓環在周邊力下的三維彈性力學解。Komijani等[10]分析了多物理場下非均勻壓電材料執行器非線性響應問題。孟廣偉等[11]利用光滑有限元理論分析了含孔功能梯度壓電材料的力電耦合行為。Almajid等[12]利用層合板理論,研究了功能梯度壓電板的離面位移和應力場。由于壓電材料是各向異性材料,材料參數較多,同時材料是非均勻性及多場耦合的情況大大增加了求解的困難。
本文基于分層法的思想,利用分層近似處理的方法[13-14]將非均勻壓電板分為若干層,每層的材料參數按照所取的指數函數進行設置,在界面處連續變化,防止出現過大的跳躍,相鄰的材料屬性有較好的連續性,從而提高其計算精度和效率。通過有限元方法建立了含裂紋的非均勻壓電板模型,在力電耦合效應下,給出了不同的梯度參數、裂紋幾何尺寸、裂紋形狀和梯度函數對裂紋周圍最大主應力,應力[σyy]和電位移分布的影響規律。本文結果可以為工程中復雜物理場下非均勻壓電材料結構的設計起到借鑒作用。
1 基本原理方程
非均勻壓電材料場方程[11]是
2 模型建立及分析
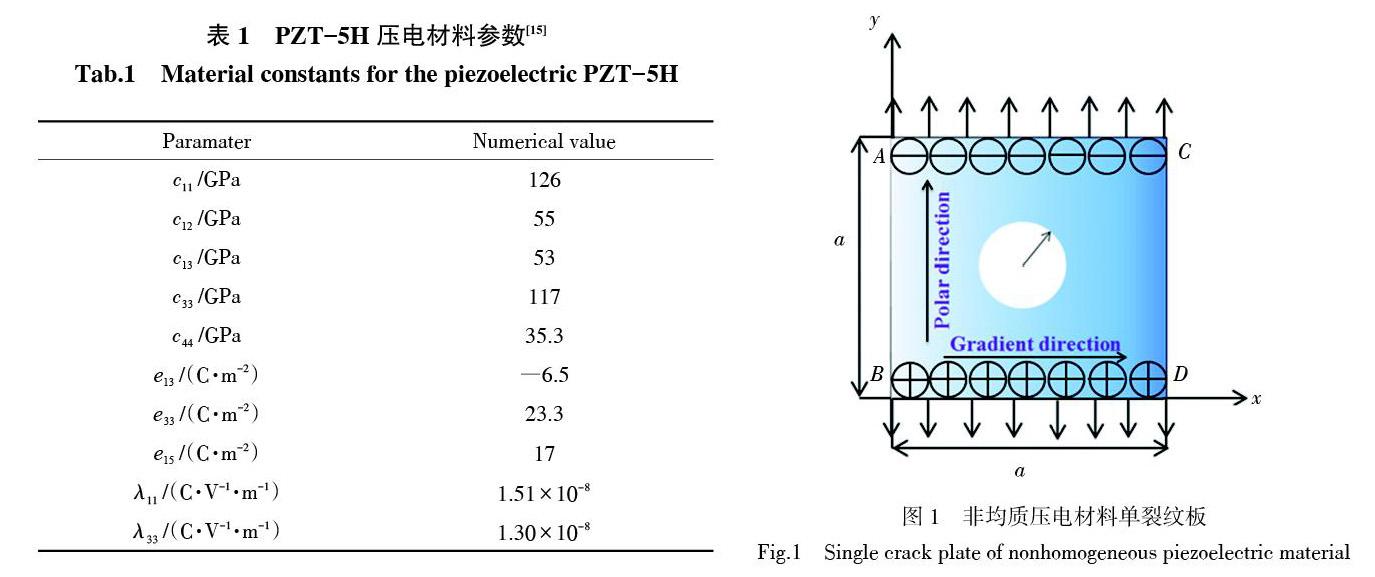
本數值模型是以含裂紋的非均勻壓電材料板作為研究對象,壓電材料的屬性[15]如表1所示。簡化的力學模型如圖1,含圓形裂紋的正方形板,邊長a=80 mm,圓形裂紋直徑r=0.5 mm,設置壓電材料的極化方向為y軸正方向,材料的梯度變化方向為x軸正方向,板的左右兩端AB與CD自由,板上下兩端同時施加力電耦合場。施加均布應力10 MPa,上端電勢為0,下端電勢為1 MV,材料參數梯度函數[K=K0eβx],其中,[K0]代表PZT-5H材料屬性[15]。這里取梯度參數[β=0.01]。
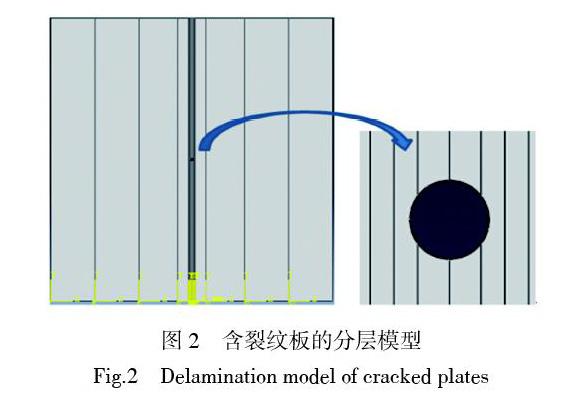
如圖2建立有限元模型,根據分層法的基本原理將模型劃分為若干層,板的層數劃分采用非均勻劃分,這樣可以更有效的分析裂紋附近場的變化。通過在圓形裂紋處的細密分層,在較遠處則分層距離擴大,對結果影響不大。在滿足一定精度情況下,將非均質板劃分為14層。每一層的材料屬性可以通過材料梯度方程計算可得,通過有限元軟件將板的材料參數賦予給每一層。板的有限元網格單元類型采用8節點CPE8RE壓電單元,保證研究結果的準確性。
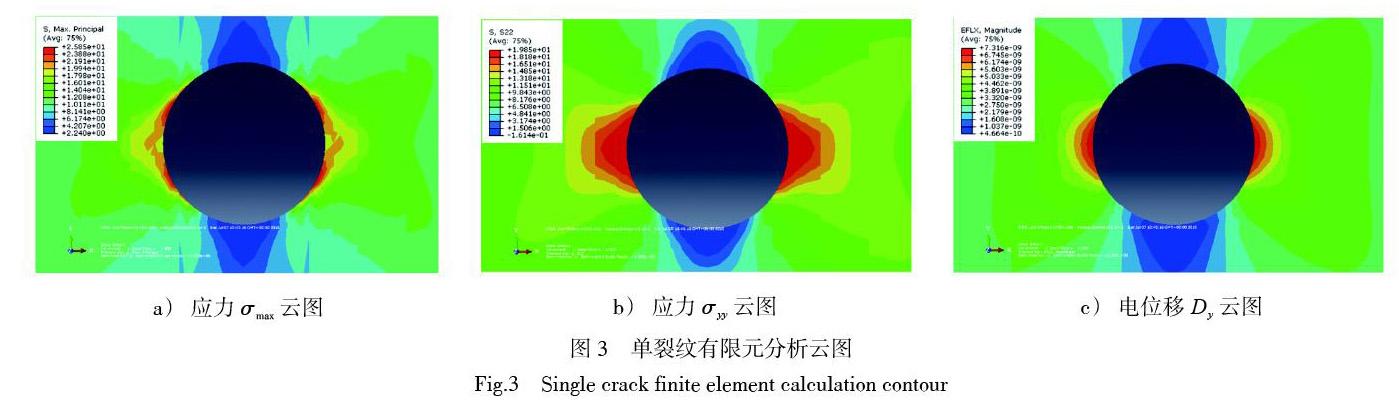
在力電耦合效應下有限元結果如圖3a)所示,可以看到裂紋周圍產生了明顯的應力集中,裂紋邊上的最大主應力值從25.85 MPa逐漸減小至2.24 MPa,但左右并不對稱。最大主應力最大的位置不是出現在裂紋尖端,這是由于材料梯度的變化,導致板左邊的彈性模量小于右邊的彈性模量,彈性模量是逐漸過渡增大,材料變得更加具有梯度性,從而避免了裂紋尖端的應力集中,使得應力分布較為均勻,限制了裂尖擴展的趨勢,達到保護板不被破壞的目的。從圖3b)中可看出,應力[σyy]集中在裂紋尖端,使得裂尖應力最大,而附近逐漸減小,這與單向拉伸裂紋應力情況相符合。圖3c)是電位移云圖,可以看出非均勻壓電板的電位移最大值集中在裂紋的尖端,在裂紋尖端周圍逐漸變小,這與文獻[14]結論相吻合。
3 算例結果分析
3.1 力電耦合效應下,梯度參數對圓形裂紋應力和電位移的影響
當非均勻壓電板在力電耦合效應下,得到在不同梯度參數[β=0.01,0.02,0.03,0.04,0.05]下的裂紋周圍的應力和電位移的分布規律,如圖4a)和圖4b)所示。當隨著梯度參數的變大,材料的非均勻性增強,非均勻壓電板左右兩端的屬性差異變大,板變得均勻性較差,裂紋更容易發生應力集中,導致最大主應力和應力[σyy]發生較大的增加。由圖4c)可得,隨著梯度參數[β]的變大,裂紋尖端的電位移[Dy]變大。
3.2 當[β=0.05]時,不同半徑對圓形裂紋應力和電位移的影響
由3.1節可知,當功能梯度參數較大時,圓形裂紋周圍的應力集中現象較為明顯,為了容易得到裂紋半徑變化和裂紋周圍的應力和電位移的關系,所以取功能梯度參數[β=0.05] 。令圓形裂紋半徑r=0.2 mm,0.5 mm,0.8 mm。設置板的大小不變時,改變圓形裂紋的半徑,可以看到圓孔附近發生了明顯的應力集中現象,如圖5a)至圖5c)所示。當裂紋較小的時候,在力、電場、力電耦合效應下,非均勻材料應力集中在小的缺陷集中區域更加容易產生,且孔徑越小應力集中越明顯,應力突然變大的趨勢變快,從而增大了裂紋周圍最大主應力與應力[σyy]。當裂紋的半徑變大后,應力集中相比較變小。而電位移[Dy]在力、電、力電耦合效應下都是隨著半徑的變大而變大。
3.3 當[β=0.01]時,橢圓形裂紋與圓形裂紋應力與電位移的比較
令梯度參數[β=0.01],且橢圓形裂紋的長軸a = r = 0.5 mm,短軸b = 0.2 mm。在力、電場、力電耦合效應一定的情況下,取相同的梯度參數,非均勻壓電材料在裂紋周圍材料屬性一致,發現橢圓形裂紋的應力和電位移要大于圓形裂紋的應力和電位移,應力集中和電位移集中現象更加明顯,這是因為橢圓形裂紋與圓形裂紋相比,裂紋的形狀更加尖銳凸出,裂紋端部承受更大的荷載,導致更容易產生明顯的應力集中和更大的電位移,材料更容易發生破壞。
3.4 當[β=0.01]時,不同梯度函數下圓形裂紋比較分析
通過可靠性問題中幾何過程的概念,本文首次提出利用幾何過程中的隨機變量序列的分布函數,來實現功能梯度材料的隨機遞增/隨機遞減的過程,這要比以往經典的梯度函數更加具有隨機性。可以通過調控“幾何過程函數”中多個參數,實現多種變化類型,更大程度上調控非均質材料的屬性。
當選取不同的梯度函數,非均質壓電材料的材料參數發生變化。這里選取第2節中自然指數[K=K0eβx]([β=0.01])時,以非均質壓電板左右兩端的材料屬性為標準。也就是,保持板左右特性不變,改變材料梯度的過渡形式。分別取線性函數、冪函數、正弦函數、幾何過程函數。最終通過計算得到各個函數中的參數值,從而得到不同類型梯度函數板在力電耦合效應下如圖7所示,裂紋的周圍的最大主應力,[σyy]應力和電位移[Dy]的分布規律。
經過分析發現,對于選定的5種不同梯度分布函數,隨著裂紋環向角度的變化,可以看到,裂紋周圍的應力和電位移在不同梯度函數下分布規律是一樣的。同時可以得到在自然指數函數情況下,裂紋周圍的最大主應力,[σyy]應力和電位移的值最小,而在其他4種函數下,數值有所差別,正弦函數>線性函數>冪函數>幾何過程函數,數值分布規律基本一致。這在一定程度上表明了不同的梯度函數作為梯度材料調控的標準,對于功能梯度材料的制造具有重要的意義,可以進一步探究。
4 結論
本文在力電耦合效應下對非均勻壓電材料的斷裂問題進行了分析。基于非均勻壓電材料的本構關系、幾何關系及邊界條件,利用分層法的理論建立了含不同裂紋類型的非均勻壓電材料有限元模型。
1)詳細討論了非均勻壓電板在力電耦合效應下,梯度參數的增大,材料均勻性變差,從而使裂紋周圍的最大主應力,應力[σyy]及電位移[Dy]增大,非均勻壓電板更加容易發生斷裂破壞。
2)分別在機械力、電場、力電耦合場作用下,研究了裂紋尺寸和裂紋形狀變化對裂紋周圍最大主應力,應力[σyy]及電位移[Dy]的影響規律,同時發現力電耦合效應要大于單一機械力或者電場的作用。
3)探究了不同梯度函數對裂紋周圍應力和電位移的影響,首次提出幾何過程函數的概念來調控非均勻壓電材料的梯度變化過程。通過研究力電耦合效應下非均質壓電材料中裂紋周圍的應力和電位移的分布規律,可為非均質壓電材料的制造使用、結構設計及其復雜工況下服役起到借鑒作用。
參考文獻:
[1] ? ?李俊峰,鄭新芳,蘇秀蘋,等. 應用PVDF壓電薄膜進行觸頭接觸壓力動態測試研究[J]. 河北工業大學學報,2014,43(4):7-10.
[2] ? ?NGUYEN V D,BECKER G,NOELS L. Multiscale computational homogenization methods with a gradient enhanced scheme based on the discontinuous Galerkin formulation[J]. Computer Methods in Applied Mechanics and Engineering,2013,260:63-77.
[3] ? ?ELOUAFI J,AZRAR L,ALJINAIDI A A. Closed-form expressions for the effective moduli of heterogeneous piezoelectric materials[J]. International Journal of Solids and Structures,2015,52:19-32.
[4] ? ?崔世堂,梁琳琳,李德龍,等. 功能梯度梁純彎曲特性研究[J]. 應用力學學報,2019,36(1):8-13,249.
[5] ? ?韓旭,龔雙. 機電耦合載荷下的壓電層合板瞬態響應分析[J]. 復合材料學報,2007,24(6):160-165.
[6] ? ?NOURMOHAMMADI H,BEHJAT B. Design criteria for functionally graded piezoelectric plates under thermo-electro-mechanical loadings[J]. Journal of Intelligent Material Systems and Structures,2016,27(16):2249-2260.
[7] ? ?張豐,徐明龍,邵恕寶. 基于菱形壓電作動器和內模控制策略的微振動隔振研究[J]. 應用力學學報,2018,35(5):956-961,1179.
[8] ? ?SELIM B A,ZHANG L W,LIEW K M. Active vibration control of FGM plates with piezoelectric layers based on Reddy's higher-order shear deformation theory[J]. Composite Structures,2016,155:118-134.
[9] ? ?張瑩,梅靖,陳鼎,等. 功能梯度圓板和環板受周邊力作用的彈性力學解[J]. 應用數學和力學,2018,39(5):538-547.
[10] ?KOMIJANI M,REDDY J N,ESLAMI M R. Nonlinear analysis of microstructure-dependent functionally graded piezoelectric material actuators[J]. Journal of the Mechanics and Physics of Solids,2014,63:214-227.
[11] ?孟廣偉,王暉,周立明,等. 含孔功能梯度壓電材料板的力電耦合無網格伽遼金法[J]. 中南大學學報(自然科學版),2015,46(11):4015-4020.
[12] ?ALMAJID A,TAYA M,HUDNUT S. Analysis of out-of-plane displacement and stress field in a piezocomposite plate with functionally graded microstructure[J]. International Journal of Solids and Structures,2001,38(19):3377-3391.
[13] ?黃立新,姚祺,張曉磊,等. 基于分層法的功能梯度材料有限元分析[J]. 玻璃鋼/復合材料,2013(2):43-48,21.
[14] ?黃干云,汪越勝,余壽文. 功能梯度材料的平面斷裂力學分析[J]. 力學學報,2005,37(1):1-8.
[15] ?SLADEK J,SLADEK V,W?NSCHE M,et al. Effects of electric field and strain gradients on cracks in piezoelectric solids[J]. European Journal of Mechanics - A,2018,71:187-198.
[責任編輯 ? ?楊 ? ?屹]

