真空動力固結軟土地基流固耦合動力特性分析

溫欣 徐東強 李偉

摘要 針對真空動力固結飽和軟土地基過程產生的大變形和流固耦合特征，基于大變形非線性有限元法構建了軸對稱流固耦合模型，并引入人工邊界條件模擬夯擊波的傳播，同時采用精細時程積分和兩點遞進格式相結合的交替迭代算法對模型進行解耦計算。結果表明：真空動力固結有效影響半徑可取2.5 r，平均有效加固深度宜取9.0 m，真空負壓和動力固結沖擊荷載相互影響對于飽和軟土地基位移增幅效果明顯，且可以顯著降低軟土地基液化的可能性。同試驗值的對比結果也驗證了數值分析的有效性。

關 鍵 詞 真空動力固結;飽和軟土地基;流固耦合;粘彈性人工邊界;交替迭代算法

中圖分類號 TU447 ? ? 文獻標志碼 A

飽和軟土地基真空動力固結過程由真空降水和動力固結多個相互影響的施工環節構成，經真空動力固結處理后的飽和軟土地基容易產生大變形[1]，呈現出明顯的流固耦合特征。孟慶山等[2]對強夯法加固飽和軟粘土地基進行了流固耦合分析，得到強夯過程中土體動態響應的一般規律;蔡袁強等[3]基于大變形理論并引入人工邊界對強夯過程中夯擊波對飽和軟土地基的影響進行了非線性有限元數值模擬分析;杜修力等[4]提出一種中心差分法和精細時程積分法相結合的顯-隱交替算法，并對飽和兩相介質進行了流固耦合動力分析;楊貝貝等[5]基于廣義偏微分方程對變形后的飽和多孔介質波動方程進行求解，同時進行了無限域動力問題的數值模擬;劉寶等[6]針對飽和多孔介質的耦合特征，引入不同耦合形式的人工邊界，探討了沖擊荷載作用下應力波在地基中的傳播特性。上述研究成果均只是基于流固耦合或者波動理論從某一個方面對飽和軟土地基的強夯過程進行了研究，而真空動力固結過程的復雜性要求有必要綜合考慮多種因素影響。本文基于大變形理論對真空動力固結飽和軟土地基進行流固耦合數值分析，并引入粘彈性人工邊界以更準確模擬夯擊波對飽和軟土地基的影響，同時采用時域交替迭代算法對流固動力耦合方程進行解耦計算，最后結合算例分析了飽和軟土地基在真空動力固結條件下的動力響應特征，研究成果有助于深入理解飽和軟土地基真空動力固結機理。

1 真空動力固結飽和軟土地基流固耦合模型構建

采用U.L.表述（Updated Lagrange）求解飽和軟土地基真空動力固結的彈塑性大變形問題。假定地基土體為層狀橫觀各向同性分布，夯錘為短圓柱體，在真空動力固結的有效影響范圍內設定截斷邊界，考慮到約束條件及荷載的對稱特點，可以用軸對稱模型對飽和軟土地基的真空動力固結過程進行數值分析。圖1為飽和軟土地基真空動力固結示意圖。

1.1 土體本構關系

真空動力固結條件下軟土的本構關系目前尚缺少深入研究，但在真空降排水和動力固結荷載作用下，飽和軟基土體會產生較大的塑性變形而達到加固效果，飽和地基土體呈現明顯的非線性變形特性，因此采用彈塑性本構模型[7]，其增量形式為

式中：[Δσ]為應力增量列陣;[Δε]為應變增量列陣;[Dep]為相關聯流動的統一強度彈塑性剛度矩陣;[De]為彈性矩陣;[Q（Q'）]為塑性勢函數;[F（F'）]為屈服函數;A與[H']為硬化函數;[σ_]為等效應力;[εp__]為等效塑性應變;[φ]為內摩擦角;[c]為粘聚力;[Rmc]為偏應力的一種度量，控制屈服面在[π]平面的性狀;p為廣義壓應力;q為廣義剪應力;[ψ]為膨脹角;[c0]為初始屈服內聚力;[e]為偏心參數，控制塑性流動勢函數與其漸近線之間的距離;[Rmv]為偏應力的另外一種度量，控制塑性勢面在[π]平面的形狀。

1.2 粘彈性人工邊界

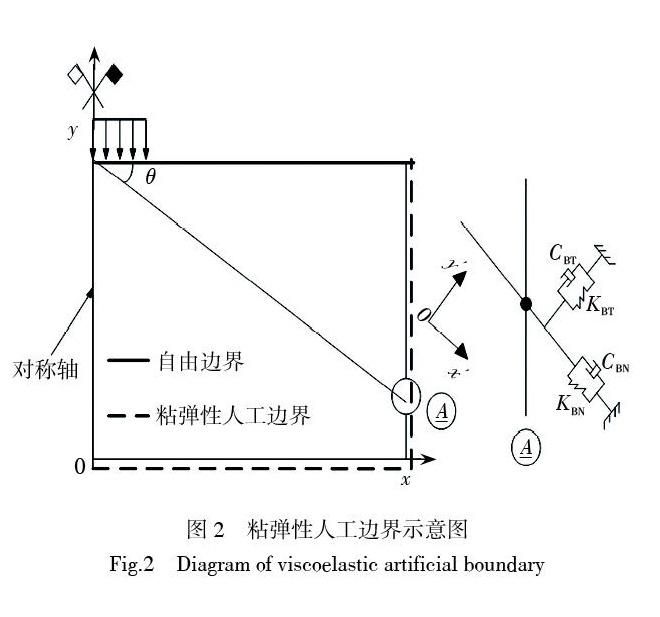
真空動力固結過程產生的波動能量將在有限元模擬的人工截取邊界上發生波的反射進而出現非真實的反射波，可以采用模擬遠域介質的彈性恢復性能的彈簧（剛度系數[KT]）和可以吸收外行波能量的阻尼器（粘滯系數[CT]）構成二維粘彈性人工邊界。

如果能精確地確定波源到人工邊界的距離[rb]，并在截斷邊界施加合適的彈簧和阻尼，即可精確地模擬波由有限域向無限域的傳播。同時借鑒脫離體概念，綜合考慮彈簧和阻尼影響，在人工邊界節點上應施加等效節點力，可以實現在粘彈性人工邊界上的波動輸入。

1.3 真空動力固結流固動力耦合模型構建

真空動力固結飽和軟土地基屬于典型的飽和兩相介質動力問題，基于改進拉格朗日法，采用Zienkiewicz[9]提出的以固相位移u和孔隙水壓力p為基本未知量的u-p模型，同時考慮土體阻尼力，將土體單元的平衡方程、本構方程及幾何方程并將粘彈性動力人工邊界條件引入飽和軟土地基真空動力固結分析中，則真空動力固結飽和軟土地基的流固耦合方程可表示為[10]

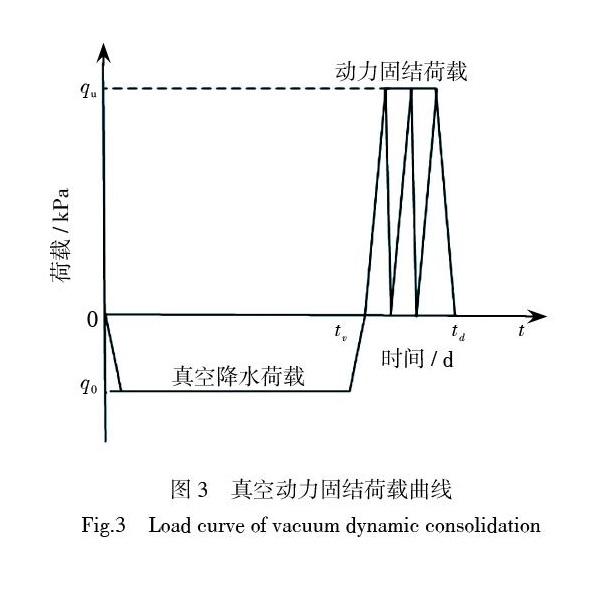
1.4 真空動力固結荷載

真空動力固結荷載由真空降水荷載和動力固結荷載組成，土體在真空荷載和動力固結荷載共同作用下開始固結。為計算方便，將真空動力固結加載曲線簡化如圖3所示。

2 方程求解

考慮到飽和軟土地基流固動力耦合方程涉及u和p兩個未知量，且存在耦合項，本次分析采用精細時程積分法[13]和中心差分法[14]相結合的交替算法以提高計算的精度和穩定性，并將耦合項作為計算當前步的初值條件，計算下一步的未知量，如此交替進行計算，其中以土體位移u為未知量的動力方程（9）引入精細時程積分法求解，以孔隙水壓力p為未知量的水體流量動力方程（10）采用兩點遞進格式計算。

2.1 土體非線性動力平衡方程的計算格式

3 工程算例及結果分析

3.1 計算說明

曹妃甸工業區某土地整理工程采用真空動力固結法處理飽和軟土地基，夯錘重量115 kN，夯錘直徑2.5 m，夯錘落距22 m。按照軸對稱取加固區一半分析，區域底面和側面的粘彈性邊界通過彈簧單元（Spring）和阻尼單元（Dashpot）實現[15]，頂面自由。初始孔隙水壓力設定為真空降水產生的負孔壓。夯擊響應時間取0.12 s[16]，流固耦合動力反應求解的時間積分算法采用前述方程解耦求解采用的交替迭代算法，時間步長Δt = 0.025 s。劃分得到192個單元和221個節點。計算參數見表1，計算斷面及單元劃分結果見圖4。

3.2 計算結果及分析

3.2.1 土體變形

通過地基土體徑向距離和夯沉量的相互關系可以確定真空動力固結軟土地基的有效加固半徑。分析圖5所示夯錘下方土體的地表沉降曲線發現：試驗值的徑向距離界限值為1倍夯錘半徑（1.0 r），而數值解結論為1.5倍夯錘半徑;在徑向距夯坑中心約2倍夯錘半徑（2.0 r）處的平均夯沉量約為峰值沉降的18%，而徑向距離為4倍夯錘半徑（4.0 r）的平均夯沉量僅為6%，試驗值和數值解曲線均呈現近似線性衰減特征，反映出土體超出界限徑向距離后整體沉降不明顯，如果以10%（平均夯沉量同峰值沉降比值）作為衡量真空動力固結有效加固半徑的標準，可以認為有效加固半徑為3.5r。但從試驗和數值分析可知，真空動力固結土體沉降影響因素眾多導致也對其有效加固半徑造成影響，建議真空動力固結有效影響半徑取值取[2.5r]。

圖6顯示了夯錘中心點A處軟土地基夯沉量沿深度的衰減情況。對應不同土層的呈現反比例變化特征的夯沉量變化符合夯擊波在成層土體中的傳遞規律。隨著深度的增加，夯擊沉降量迅速變小，試驗觀測發現距離地表2.0 m處的土層平均沉降量為159 cm，而當達10 m時沉降量為8 cm，僅占總沉降量的5%，真空動力固結對土體的影響已經很小。而數值解沉降計算結果顯示其有效影響深度小于試驗值，分析原因在于后者推導過程假設滲透系數、有效應力同孔隙比的非線性關系，2種方法計算條件存在差異導致。因此，可以認為真空動力固結的平均有效加固深度近似為9.0 m。

3.2.2 孔隙水壓力

分析真空動力固結軟土地基第一遍動力固結階段孔隙水壓力曲線（圖7）發現：試驗和數值分析均呈現出典型的峰值特征，數值解孔壓峰值相比試驗值結果相差15%，且同后者相比存在一定滯后性，同時超孔壓消散幅度相對較慢，曲線整體特征相似，表明了數值方法進行孔壓分析的合理性。

3.2.3 土體應力

圖8為飽和軟基各層土體應力[pi]與錘底接觸應力[p0]的比值曲線。分析發現：真空動力固結條件下地基土中附加應力沿深度方向有所減小，即隨著土體附加應力比增大，土體沉降深度逐漸減小，曲線變化形狀同現場數據基本一致。這說明真空降水后的淺層土體的動力固結夯擊能消耗單純動力固結大，并可顯著降低軟土地基液化的可能性。

4 結論

本文對飽和軟土地基真空動力固結過程進行流固耦合數值分析，分析了真空動力固結條件下飽和軟土地基的動力響應特征，得到如下結論。

1）基于U.L.表述和非線性有限元方法，同時考慮粘彈性人工邊界以模擬夯擊波影響，對飽和軟土地基真空動力固結過程進行流固耦合數值分析，并采用精細時程積分和中心差分交替迭代算法進行解耦計算，數值分析結果符合飽和軟基土體變形規律，具有較好的可靠性，有助于深入理解飽和軟土地基真空動力固結機理。

2）真空動力固結土體沉降影響因素眾多導致也對其有效加固半徑造成影響，真空動力固結有效影響半徑取值可取[2.5r]，真空動力固結的平均有效加固深度近似為9.0 m。

3）真空動力固結對于飽和軟土地基位移的增幅效果明顯，隨著土體排水固結導致位移沉降變化不明顯;真空降水后的淺層土體的動力固結夯擊能消耗單純動力固結大，并可顯著降低軟土地基液化的可能性。

參考文獻：

[1] ? ?朱允偉，韓選江，李玉國. 真空動力固結法處理軟基效果的試驗研究[J]. 地下空間與工程學報，2008，4（1）：175-180.

[2] ? ?孟慶山，雷學文. 飽和軟粘土強夯的流、固耦合分析[J]. 武漢科技大學學報（自然科學版），2000，23（4）：364-366.

[3] ? ?蔡袁強，陳仁偉，徐長節. 強夯加固機理的大變形數值分析[J]. 浙江大學學報（工學版），2005，39（1）：65-69.

[4] ? ?杜修力，宋佳，李亮. u-p格式飽和兩相介質動力問題的顯-隱式交替算法[J]. 巖土工程學報，2016，38（3）：395-403.

[5] ? ?楊貝貝，李偉華，趙成剛，等. 基于Comsol的飽和多孔介質動力方程的數值模擬及應用[J]. 地震工程學報，2017，39（2）：321-328.

[6] ? ?劉寶，蘇謙，劉亭，等. 飽和多孔介質不同動力耦合形式數值分析[J]. 振動與沖擊，2017，36（9）：146-152，213.

[7] ? ?盧廷浩，劉祖德，陳國興. 高等土力學[M]. 北京：機械工業出版社，2006.

[8] ? ?沈聚敏，周錫元，高小旺. 抗震工程學[M]. 第2版. 北京：中國建筑工業出版社，2015.

[9] ? ?ZIENKIEWICZ O C，CHANG C T，BETTESS P. Drained，undrained，consolidating and dynamic behavior assumptions in soils[J]. Geotechnique，1980，30（4）：385-395.

[10] ?趙伯明，夏晨. 多源輸入條件下的黏彈性人工邊界研究[J]. 土木工程學報，2015，48（增刊1）：147-151.

[11] ?中交天津港灣工程研究院有限公司. 港口工程地基規范（JTS147-1-2010）[S]. 北京：人民交通出版社，2010.

[12] ?郭見揚. 強夯夯錘的沖擊力問題（強夯加固機理探討之一）[J]. 土工基礎，1996，10（2）：35-39.

[13] ?鐘萬勰. 結構動力方程的精細時程積分法[J]. 大連理工大學學報，1994，34（2）：131-136.

[14] ?劉晶波，杜修力，李宏男，等. 結構動力學[M]. 北京：機械工業出版社，2005.

[15] ?費康，張建偉. ABAQUS在巖土工程中的應用[M]. 北京：中國水利水電出版社，2010.

[16] ?裘以惠，郭玉玲. 強夯法加固地基的土體動應力量測[J]. 太原工學院學報，1984，15（1）：45-52.

[責任編輯 ? ?楊 ? ?屹]