基于子結構的周期性結構設計方法
吳紫俊 肖人彬
摘要 針對傳統基于均勻化方法的周期性結構設計宏微尺度分離問題,提出了基于有限元子結構的周期性結構設計方法。在該方法中,假設宏觀結構由構型相同的多個子結構構成。在宏觀層面,利用子結構凝聚構建了超單元計算模型;在微觀層面,采用SIMP優化方法建立了子結構內部單元的拓撲構型設計方法。通過反求超單元模型計算結果,實現了宏微觀結構的耦合計算。在耦合計算過程中,由于超單元之間具有公共的部分邊界,使得子結構構型間具有良好的材料連通性。同時,子結構劃分源于宏觀設計域的有限元網格,確保了宏微結構間具有明確的尺寸比例關系。最后,通過兩類梁的計算實例,驗證了所提方法的有效性。
關 鍵 詞 子結構;周期性;微結構;拓撲優化
中圖分類號 TB383.3 ? ? 文獻標志碼 A
0 引言
周期性結構設計是現代結構設計的重要分支[1],已被廣泛應用于多個領域,如航空[2]、汽車[3]等的結構設計。周期性結構不僅承載能力強,重量輕[4-5],還具有隔熱[6]、隔音[7]等多功能物理特性,因其獨特的結構組成形式和良好的設計加工性能,展現出了廣闊的研究和應用前景[8-9]。周期性結構設計是一種多尺度的拓撲優化設計,方法上可分為2類:一類是基于均勻化的設計方法[10];另一類是基于宏觀周期性約束的設計方法[11]。
均勻化方法設定材料的宏觀結構由微觀尺度的單胞周期性拓展而形成。周期性結構的單胞具有周期性應力和應變邊界條件,從而獲取單胞內材料的最優分布,實現不同結構性能的周期性單胞設計[12]。Vogiatzis等[13]基于水平集法提出了單相和多相負泊松比材料的設計方法,通過施加周期性的Dirichlet位移邊界條件得到周期性微結構,并采用最速下降法構建微結構內部構型。Fantoni等[14]提出了一種多場漸近均勻化方法,用以分析具有周期性微結構的壓電材料,利用周期攝動函數考慮具有代表性的微結構非均勻性的影響。Hunag等[15]將雙向進化結構優化方法推廣到具有最佳粘彈性特性的復合材料微觀結構設計中,基于均勻化方法計算復合材料的性能參數,通過BESO方法實現單胞內材料的重新分配。賈嬌等[16]研究了宏觀傳導條件對材料微結構的影響,并提出了基于宏觀傳導條件的周期性結構傳熱材料的研究,構建了基于變密度法周期性傳熱結構模型。杜義賢等[17]基于能量均勻化方法研究了抗剪性能更優的周期性點陣結構,并提出了基于經典胞元理論的周期性點陣結構的面內等效切變模量的解析表達式。
在均勻化方法中,微觀單胞與宏觀結構設計是相互耦合的設計過程,對微觀結構的宏觀有效性材料進行評價的同時,宏觀結構的計算結果也影響微觀結構的構型優化[18]。采用均勻化方法進行周期性結構設計,其尺度分離假設會帶來2個問題:一個是微結構單胞間材料的連通性[19],其微結構單胞優化是一個獨立的優化過程,宏觀位移或應力的變化往往引起微結構間材料不連通,使得所優化的結果只有理論構型,不具備制造性[20];另一個是均勻化方法假設微結構與宏觀結構的尺寸比例約為10-9,當該比例接近于1時往往得不到合適的優化構型[21-22]。
宏觀周期性約束的設計方法中,宏觀結構被均勻地劃分成若干個具有特定長度比例大小的單元胞體。每個單元胞體同一位置上的單元具有相同的材料密度值和靈敏度值[23]。優化變量為單元胞體中每個單元的材料密度。與均勻化方法相比,隨著單元胞體的細化,其優化結果逐漸近似于均勻化方法設計結果。在基于BESO方法的周期性結構設計中[24],需要在整個設計域中求解具有周期性邊界約束的方程,存在計算量大的問題[25]。
為解決均勻化方法的尺度分離問題和宏觀周期性約束設計方法中計算量過大的問題[26],本文在有限元子結構方法的基礎上,提出了利用子結構凝聚構建宏觀結構的超單元計算模型,采用SIMP優化方法[27-28]建立子結構內部單元拓撲構型設計的周期性結構設計方法。
1 子結構凝聚及周期性結構優化問題定義
1.1 子結構凝聚
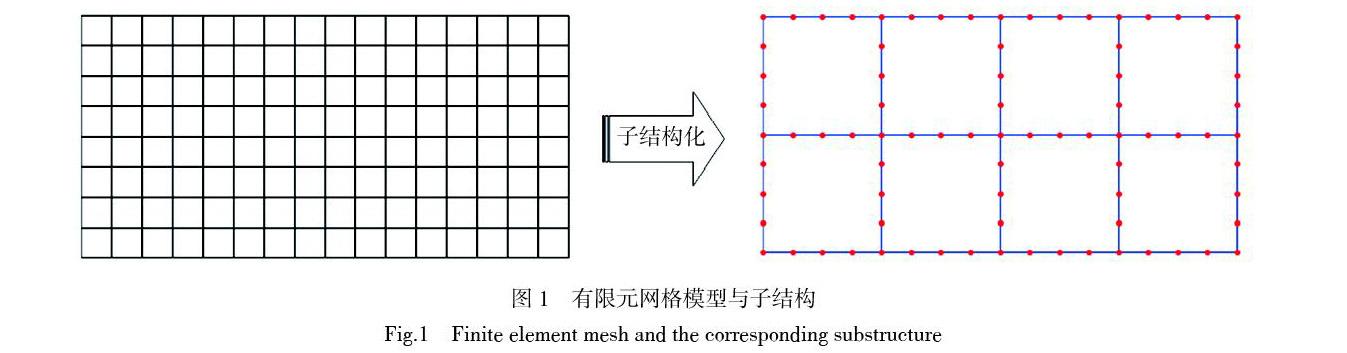
根據有限元子結構的定義,有限元網格模型可以重新劃分為多個子結構[29],如圖1所示。
優化目標是宏觀周期性結構的最小化柔度;設計變量為周期性子結構中包含的n個單元的相對密度[ρj];[K]、F分別為子結構對應超單元組裝的整體剛度矩陣與外載荷向量,[Ubb,i]是第i個超單元的位移向量,[V]是當前周期性子結構所含的材料體積,N為宏觀結構的子結構總數。
2 基于子結構的周期性結構優化模型
2.1 宏觀尺度模型
在周期性結構的宏微結構優化中,宏觀結構的剛度矩陣由式(5)建立。由于省略了內部節點,可提高其計算效率。而子結構的內部節點的位移可根據式(2)獲得。此時,圖1中的子結構模型的剛度矩陣可表示為
此時,所優化的結構將分布在整個宏觀設計域中。在宏觀結構計算過程中,其構建剛度矩陣的周期性子結構均有相同構型,對應的每個超單元凝聚矩陣均相同,即[K*bb,t=K*bb,s,t≠s] 。
2.2 子結構優化模型
在子結構構型的優化中,需要增加懲罰因子p對拓撲優化設計變量的密度進行懲罰,使其收斂于設定的密度上下界,從而獲得子結構的“黑白”設計[30]:
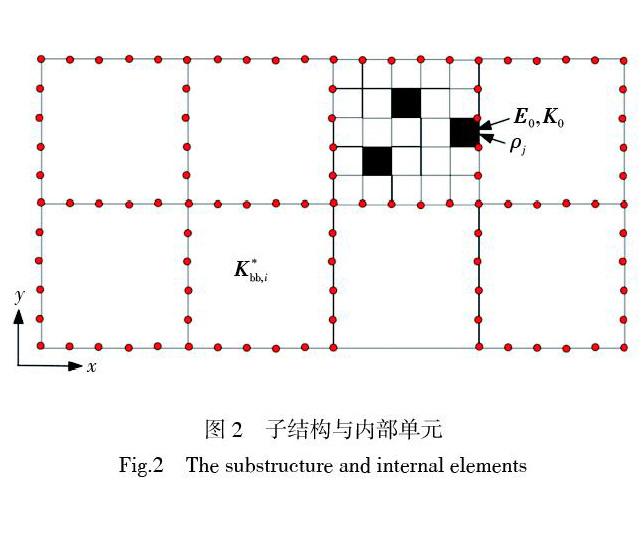
式中,懲罰因子[p≥1]表明具有中間密度的子結構[0<ρj<1]的剛度矩陣會被懲罰。該懲罰因子值越大,其優化結構桿系特征越明顯。式中,n表示該子結構內部的有限元單元總數,[Κ0]為實體材料下的有限元單元剛度矩陣,如圖2所示。
與傳統的SIMP方法不同,此時的懲罰因子p對子結構剛度矩陣的懲罰,不是凝聚后的超單元對應的剛度矩陣,而是子結構內所有單元對應的有限元單元剛度矩陣。當子結構構型優化結束后,需對其進行二次凝聚,從而在宏觀結構中計算每個子結構邊界的位移,實現宏微結構的下一次迭代計算。
2.3 靈敏度計算及變量迭代
根據所建立的子結構代理優化模型,上述基于子結構的周期性結構設計問題可重新定義為
式中:[κ]為拉格朗日因子,該因子可通過分半算法強制使設計域中的材料滿足體積約束;體積導數[?V?ρj=vj]為每個子結構的體積約束,在此與子結構當前的材料體積相等。
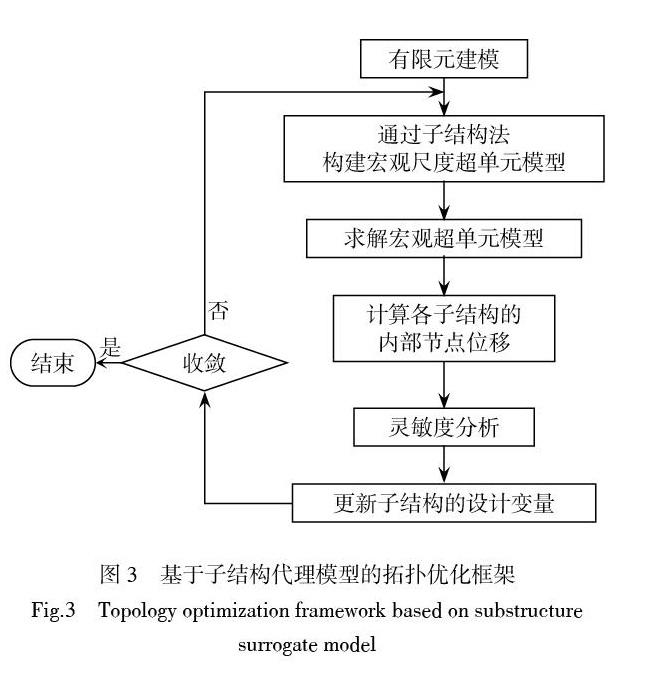
在優化迭代計算中,通過OC方法進行變量更新,每個子結構的初始體積約束均相等,整個設計域在整個優化過程中的材料體積與初始設置的體積約束相等。即材料體積始終不變,優化過程只在周期性子結構中尋找材料的最優分配比例,達到最優設計。對應優化框架如圖3所示。
3 數值計算實例
3.1 雙端固支梁結構設計
以雙端固支梁的拓撲優化設計為例[31],設計域大小為[L1×L2=2×1],其左右兩側固定,設計域中央承受[F=1]的垂直向壓力如圖4所示。所選用材料的彈性模量為[E0=1],柏松比[υ0=0.3]。
把宏觀設計域劃分為3種不同數量的子結構:[Nx×Ny=2×1],[Nx×Ny=4×2]和[Nx×Ny=8×4];子結構分別設置為[30×30],[50×50]兩類不同單元數的單元集合。根據宏觀模型的定義,在優化過程中,設體積約束設置為0.3,由于宏觀結構中沒有設計變量,因此每個周期性子結構的體積約束也為0.3。在周期性子結構的優化中,當懲罰因子設置為1,所優化的周期性子結構拓撲結構中存在大量的中間密度單元,沒有明顯的桿系結構特征。為了得到更為精細的局部結構特征,在此把懲罰因子設置[p=3]。優化迭代步長設置為0.02,為避免周期性子結構中出現棋盤格現象,靈敏度的過濾半徑設置為子結構內部單元長度的1.5倍,當相鄰兩次目標函數值相對誤差小于0.000 1時所得拓撲構型即為最優結構。其優化結果如表1所示。
從優化結果中,可推斷出以下結論:1)相同的宏觀結構子結構劃分,優化時所選取的子結構大小不同,其最終的優化拓撲構形也不同,其宏觀結構的柔度值隨著子結構單元數增多而減小;2)在同一大小的子結構下,宏觀結構子結構劃分不同,最終優化的周期性子結構構形基本相似,其宏觀結構的柔度值隨著子結構數量增多而逐漸增大。當子結構所含單元數增多時,意味著設計域的有限元網格更為細化,所得到的宏觀優化結構特征越精細,其優化結構的柔度值越小。
從優化結果看,微結構邊界間具有良好的材料連通性,改變了文獻[18]中由于應變場突變引起的微結構間材料不連通的情況,為其結構加工制造提供了模型基礎。同時,設計過程中宏觀結構與微觀構型間具有明確的尺寸比例關系,保證了設計出的結構性能與實際制造出的結構性能的一致性,避免了均勻化方法中因尺度分離引起的結構設計與制造的性能誤差。
3.2 懸臂梁結構設計
在懸臂梁的拓撲優化設計中,設置設計域大小為[L1×L2=2×1],其左側固定,設計域右上方角點承受[F=1]的垂直向壓力如圖5所示。所選用材料的彈性模量為[E0=1],柏松比[υ0=0.3]。
把宏觀設計域劃分為3種不同數量的子結構:[Nx×Ny=2×1],[Nx×Ny=4×2]和[Nx×Ny=8×4];子結構設置為[40×40]的單元集合。為驗證懲罰因子對優化構型的影響,分別設置懲罰因子[p=1]和[p=2]。靈敏度的過濾半徑設置為子結構內部單元長度的1.2倍,優化迭代步長設置為0.02,當相鄰兩次目標函數值相對誤差小于10-4時所得拓撲構型即為最優結構。其優化結構如表2所示。
從優化結果中可以看出:當懲罰因子設置為1,所優化的周期性子結構拓撲結構中存在大量的中間密度單元,沒有明顯的桿系結構特征,隨著懲罰因子的增大,其桿系特征逐漸明顯。同時,最優宏觀構型的柔度值隨著懲罰因子和宏觀子結構劃分數的增大而增大。從優化結構來看,所得到的宏觀結構及其對應的微觀構型,其材料具有很好的連通性,因此所得構型具有良好的可制造性。
需要注意的是由于SIMP方法中懲罰因子的影響,使得子結構內部有限元單元的相對密度不是離散的0或1。盡管通過子結構方法可獲得具有良好材料連通性的優化結構,但是所產生的中間密度單元給制造帶來了困難。
4 結論
本文提出了一種基于子結構的周期性微結構拓撲優化方法,解決了傳統均勻化方法中尺度分離引起的微結構間材料不連通和結構設計與制造間性能誤差的問題,為設計制造一體化提供了一種參考方法。本文研究結論可歸納如下。
1)通過子結構凝聚構建宏觀結構的超單元計算模型,把宏觀結構尺寸信息帶入到了微結構中,同時,通過引入超單元間的共同部分邊界確保了微結構設計過程中材料的連通性。
2)優化計算結果表明,宏觀子結構劃分與子結構內部有限元網格越多,其優化構型的桿系特征越明顯。由于采用的變密度法SIMP,當懲罰因子取值較小時,得到大量的中間密度單元。
3)采用SIMP方法,不可避免存在中間密度單元,給實際加工制造帶來困難。同時,所設計的宏微結構模型邊界存在臺階現象,因此需要在可加工性方面做進一步的改進。
參考文獻:
[1] ? ?ZHU J,ZHANG W,BECKERS P. Integrated layout design of multi-component system[J]. International journal for numerical methods in engineering,2009,78(6):631-651.
[2] ? ?LIU S,HU R,LI Q,et al. Topology optimization-based lightweight primary mirror design of a large-aperture space telescope[J]. Applied optics,2014,53(35):8318-8325.
[18] ?XIA L,BREITKOPF P. Multiscale structural topology optimization with an approximate constitutive model for local material microstructure[J]. Computer Methods in Applied Mechanics and Engineering,2015,286:147-167.
[19] ?SIVAPURAM R,DUNNING P D,Kim H A. Simultaneous material and structural optimization by multiscale topology optimization[J]. Structural and multidisciplinary optimization,2016,54(5):1267-1281.
[20] ?LI H,LUO Z,GAO L,et al. Topology optimization for functionally graded cellular composites with metamaterials by level sets[J]. Computer Methods in Applied Mechanics and Engineering,2018,328:340-364.
[21] ?ZHU Y,LI S,DU Z,et al. A novel asymptotic-analysis-based homogenisation approach towards fast design of infill graded microstructures[J]. Journal of the Mechanics and Physics of Solids,2019,124:612-633.
[22] ?LI Q,XU R,LIU J,et al. Topology optimization design of multi-scale structures with alterable microstructural length-width ratios[J]. Composite Structures,2019,230:111454.
[23] ?XIE Y M,ZUO Z H,Huang X,et al. Convergence of topological patterns of optimal periodic structures under multiple scales[J]. Structural and Multidisciplinary Optimization,2012,46(1):41-50.
[24] ?XIA L,XIA Q,HUANG X,et al. Bi-directional evolutionary structural optimization on advanced structures and materials:a comprehensive review[J]. Archives of Computational Methods in Engineering,2018,25(2):437-478.
[25] ?FU J,XIA L,GAO L,et al. Topology optimization of periodic structures with substructuring[J]. Journal of Mechanical Design,2019,141(7):071403.
[26] ?HOU Y,ZHAO Q,Sapanathan T,et al. Parameter identifiability of ductile fracture criterion for DP steels using bi-level reduced surrogate model[J]. Engineering Failure Analysis,2019,100:300-311.
[27] ?BENDS?E M P,SIGMUND O. Material interpolation schemes in topology optimization[J]. Archive of applied mechanics,1999,69(9-10):635-654.
[28] ?SIGMUND O. A 99 line topology optimization code written in Matlab[J]. Structural and multidisciplinary optimization,2001,21(2):120-127.
[29] ?WU Z,XIA L,Wang S,et al. Topology optimization of hierarchical lattice structures with substructuring[J]. Computer Methods in Applied Mechanics and Engineering,2019,345:602-617.
[30] ?BENDS?E M P,SIGMUND O. Topology optimization:theory,methods and applications[M]. Berlin:Springer-Verlag,2003.
[31] ?ALEXANDERSEN J,LAZAROV B S. Topology optimization of manufacturable microstructural details without length scale separation using a spectral coarse basis preconditioner[J]. Computer Methods in Applied Mechanics and Engineering,2015,290:156-182.
[責任編輯 ? ?楊 ? ?屹]

