ANSYS在壓電天平設計中的應用

趙榮娟, 黃 軍, 劉施然, 呂治國, 李國志

(中國空氣動力研究與發展中心 超高速空氣動力研究所, 四川 綿陽 621000)

0 引 言

壓電天平是利用壓電材料的正壓電效應來進行測量的天平，主要用于脈沖風洞中的氣動力測量試驗[1-2]。常用的壓電天平有3種：一種以美國康奈爾航空試驗室(GAL)早期研制的壓電天平為代表，直接采用無彈性壓電元件組合測量氣動特性[3]；一種是中國空氣動力研究與發展中心(CARDC)研制的具有彈性元件的梁式微應變壓電天平；一種是直接采用壓電型力傳感器進行氣動特性測量的壓電天平[4]。

梁式微應變壓電天平采用粘貼在天平力敏梁上的壓電陶瓷片來感受力敏梁的變形，從而達到在風洞中測量模型所受氣動力的目的。由于壓電陶瓷材料具有很高的頻響和較大的壓電常數，天平的剛度可以做得較高，從而提高了天平的頻響范圍，可用于激波風洞等脈沖風洞的測力試驗。

但在激波風洞的有效試驗時間內(一般為毫秒量級，在幾毫秒至幾十毫秒之間)，模型、天平和支撐系統在風洞啟動時受到的沖擊振動得不到完全阻尼，天平輸出的是多種頻率的振動信號和有效試驗信號的疊加信號，必須采用慣性補償方法去除振動信號，以得到有效的試驗信號。能否有效地去除振動信號，是制約風洞試驗數據質量的一個重要因素。在慣性補償設計中，一般采用加速度計進行慣性補償：通過合理設計加速度計的安裝位置，使得加速度計僅感受慣性振動信號；在試驗前，通過動態校準試驗獲得慣性補償系數[2-8]。

目前，有限元分析方法已廣泛應用于模擬求解真實的工程問題，尤其是在各種結構和傳感器的設計中[9-10]。在風洞天平設計領域，有限元分析方法被用于評估天平敏感梁微應變和結構變形均勻性以預估天平的性能[11-16]。ANSYS力電耦合的有限元分析方法在壓電型傳感器、俘能器、驅動器[17-21]等設計中具有較多應用。在壓電天平設計領域，ANSYS有限元分析方法基本上是用于結構分析，采用力電耦合方法評估天平整體性能的研究工作則少有報道[22-25]。

在本文研究中，將壓電天平結構本體和壓電陶瓷片作為一個整體，分別對壓電天平結構本體和壓電陶瓷片進行建模，采用力電耦合的求解方法，直接得到各種載荷作用下天平各分量壓電陶瓷片上的輸出開路電壓，可以更直觀地評估壓電天平性能；同時對加速度計的輸出進行評估，可以直接檢驗加速度計慣性補償的效果。

1 有限元分析的基本理論

有限元分析方法的核心思想是將被分析物體(連續的求解域)離散為有限個單元，每個相鄰單元通過單元間的公共界面或邊界面彼此連接。對每一個單元建立方程，集合為一組聯立代數方程組，可得到整個物體的解答。有限元法可以解決結構分析、熱傳導、流體力學的流場分析、電磁場分析等問題[10]。

在本文研究中，主要使用了ANSYS軟件中的結構分析和壓電分析模塊。

1.1 力電耦合動力學模型

在壓電結構的本構關系中，除彈性變形關系外，還存在力電耦合作用和介電作用。通常其本構關系可用如下2個壓電方程(壓電彈性方程、電荷方程)描述：

T=cES-eE

(1)

D=eTS+εSE

(2)

式中各變量的定義為：T為壓電應力矩陣；D為壓電輸出電位移矢量；S為壓電應變矩陣；E為電場強度矢量；cE為結構彈性矩陣；e為壓電應力常數矩陣；εS為常應變下的壓電材料介電常數矩陣。

上述2個方程用于描述壓電結構的逆壓電效應和正壓電效應。正壓電效應可用于設計各類傳感器。本文的壓電天平傳感器僅外載荷已知，需要同時求解整體結構的力學響應和電響應，因此需要聯立2個壓電方程進行求解。

利用ANSYS有限元分析軟件的前處理功能，完成幾何建模、單元類型定義、材料屬性定義、網格劃分、耦合節點處理以及載荷施加，可以在軟件后臺獲得如下形式的壓電天平整體結構的動力學方程：

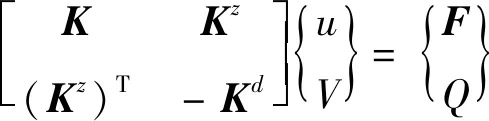
(3)

其中，u和V分別為整體結構的位移響應和輸出電勢響應，M、C、K分別為結構的質量陣、阻尼陣和剛度陣，F為結構載荷矢量，Kz、Kd分別為壓電耦合矩陣和壓電介電系數矩陣，Q為壓電結構電極面上的輸出電荷量，Cvh為壓電介電阻尼矩陣，其影響通常可忽略。若考慮壓電陶瓷片開環輸出情況，式(3)可改寫為：

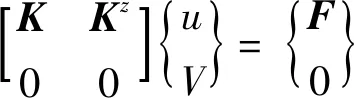
(4)

1.2 模態分析模型

模態特征是機械結構的固有振動特性，每個模態具有特定的固有頻率、阻尼比和模態振型。對于壓電結構，主要針對其彈性振動特性進行模態分析。由式(3)可得線性自由振動方程：

(5)

對壓電結構進行模態分析，即求解式(4)的特征值問題，即：

Kφ-ω2Mφ=0

(6)

其中，φ為模態振型矩陣，ω為模態頻率。

1.3 靜力學分析模型

靜力分析用于計算結構在固定不變的載荷下的響應，是ANSYS默認的分析類型。該分析不考慮結構的慣性和阻尼影響，即忽略式(3)中所有慣性項和阻尼項的作用，適用于求解慣性和阻尼對結構響應的影響不重要的問題。

1.4 瞬態動力學分析模型

動力學分析用于求解隨時間變化的載荷對結構或部件的影響。與靜力分析不同，動力學分析需考慮隨時間變化的力載荷及其對阻尼和慣性的影響。

本文的瞬態動力學分析用于求解天平在瞬態載荷沖擊條件下的響應。在動力學分析中必須考慮阻尼項，否則不能獲得收斂的振動響應結果。本文采用Rayleigh阻尼的施加方式，即首先假設結構的前兩階模態阻尼系數為ξ1=ξ2=0.08%，然后以下式計算Rayleigh阻尼比例系數：

αM=2(ξ1ω2-ξ2ω1)/(ω2/ω1-ω1/ω2)

(7)

βK=2(ξ2/ω1-ξ1/ω2)/(ω2/ω1-ω1/ω2)

(8)

則最終的阻尼矩陣C為：

C=αMM+βKM=0

(9)

2 壓電天平的結構

本文設計的壓電天平是一臺三分量梁式微應變天平。天平力敏梁的橫截面為矩形，通過壓電陶瓷片極性的組合實現分量間的抗干擾特性。當氣動力作用于模型，天平力敏梁發生變形，粘貼其上的壓電陶瓷片輸出電荷，電荷量與力敏梁變形程度相關，通過檢測電荷量即可測量作用于模型的氣動力。天平前端通過錐段與模型連接，后端通過錐面配合、雙頭螺母拉緊的方式與模型支桿連接。

3 天平結構的有限元分析

3.1 有限元模型

在有限元建模時，壓電陶瓷片采用正壓型的PZT-5，天平本體采用00Ni18Co8Mo5TiAl材料(性能參數見表1。表中，c為彈性剛度矩陣元；E、ρ、μ分別為彈性模量、密度、泊松比；ε為介電常數；e為壓電應力常數)。采用SOLID5壓電耦合單元模擬壓電陶瓷片(壓電陶瓷片上會出現力場和壓電場耦合，而SOLID5單元具有三維磁場、熱場、電場、壓電場和結構場分析能力，并能在各場之間實現有限的耦合)；采用SOLID45單元模擬天平本體。建立的壓電天平有限元模型如圖1所示。

圖1 壓電天平的有限元模型

表1 材料參數表Table 1 Material parameters

3.2 天平模態分析

模態分析的主要目的是獲得天平的各階振動頻率和振型，以判斷其是否滿足激波風洞測量的需求。本文主要計算了壓電天平的前6階固有頻率和相應的振型(如圖2所示)，可以看出：壓電天平的一階和二階振型分別為天平支桿沿側向和法向的擺動(力敏梁的寬度和高度分別為20和22 mm，因此一階和二階振動頻率有少許差異)；三階振型為天平支桿沿軸線的滾轉運動；四階和五階振型為天平支桿沿法向和側向的彎曲擺動；六階振型為天平支桿沿軸向的伸縮運動。

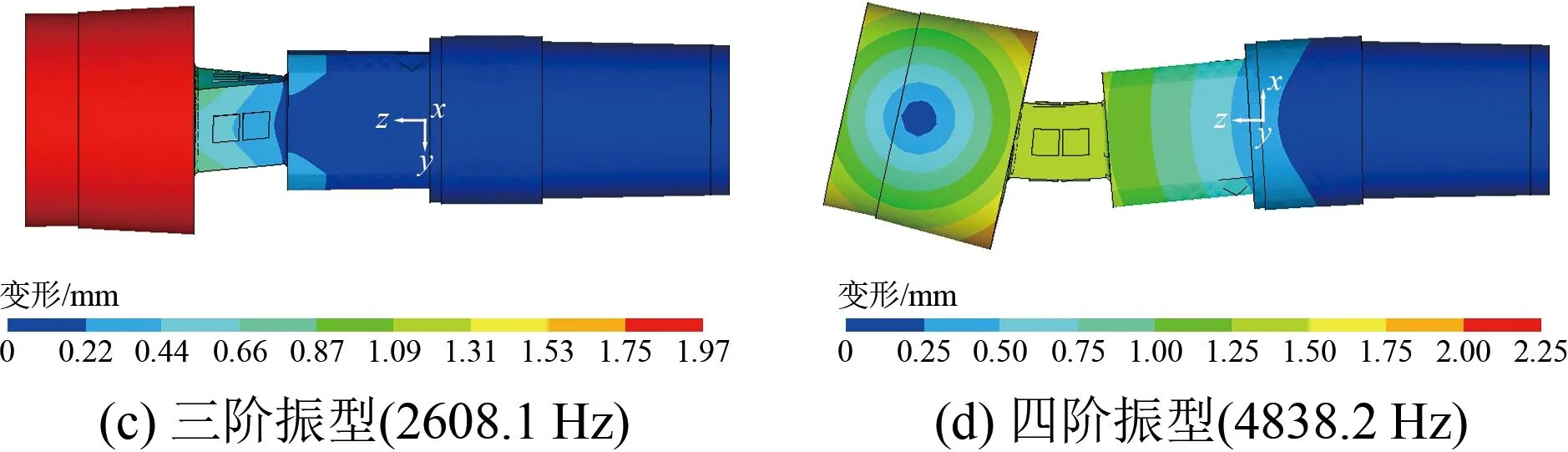
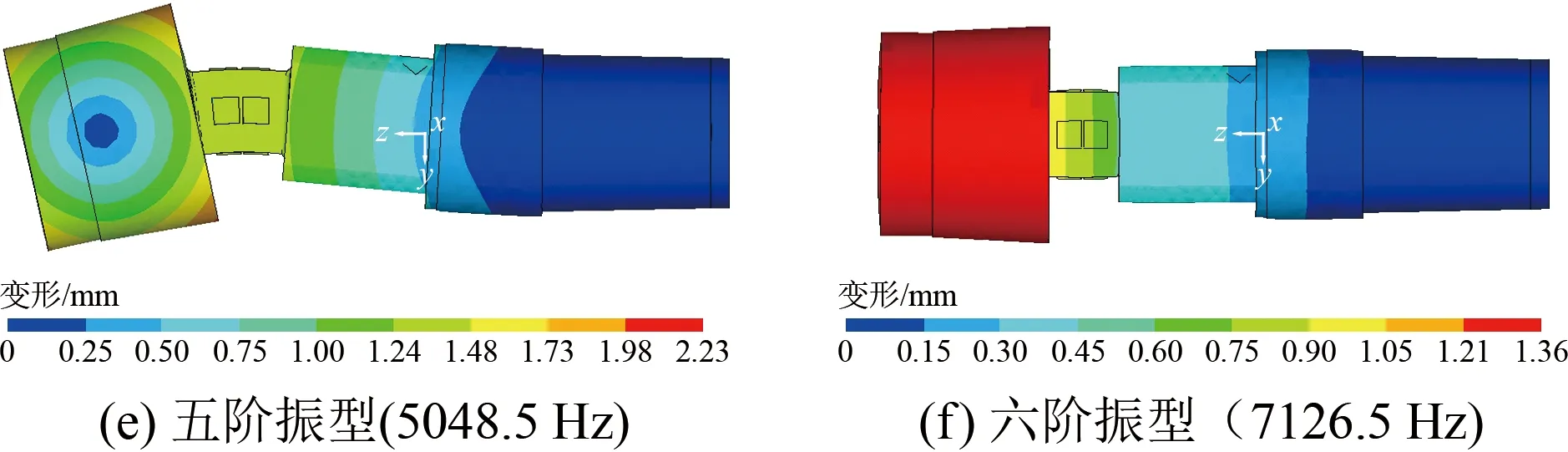
圖2 壓電天平前6階振型

模態分析結果表明：壓電天平的頻響相對較高，前兩階振動頻率均超過1 kHz，可以滿足激波風洞測力試驗的需求。

3.3 靜力分析

壓電天平的靈敏度、線性度、抗干擾能力是其設計的關鍵，以ANSYS軟件進行靜力分析的方法能夠獲得上述性能指標，從而很好地評估天平設計的合理性。靜力分析的目的就是為了獲得天平輸出與施加載荷之間的關系。本文在不同加載條件下計算了天平各分量的電壓輸出情況，評估天平各分量的主靈敏度系數和干擾靈敏度系數。

采用類似天平單元校準的方案，即一次只施加一個載荷，得到天平各分量的輸出，取主分量電勢輸出為Vz，其他干擾分量電勢輸出為Vgi，則主靈敏度系數εz可以定義為主分量輸出電勢Vz和外加載荷Fz的比值，而干擾靈敏度系數εgi是其他分量輸出電勢Vgi和外加載荷Fz的比值：

εz=Vz/Fz

(10)

εgi=Vgi/Fz

(11)

3.3.1 加載方案

在靜力分析的加載中，為了實現在天平力矩中心加載，在模型中應用附加質量和局部剛度化處理。在天平的力矩中心生成一個節點，設置為質量單元，質量為1×10-12kg，將該節點與天平前端連接錐面上的節點通過局部剛度化進行耦合處理，再將該節點作為加載點分別進行力、力矩以及綜合加載。這樣處理的好處是：在進行法向力加載時，可以避免引入附加的俯仰力矩干擾，從而得到更為準確的主靈敏度系數和干擾靈敏度系數計算結果。

3.3.2 天平各分量靈敏度分析

在軸向力加載中，分別進行了10、100、200、350和500 N的加載。從各加載條件下天平各分量輸出電壓(表2)可見，軸向力分量VA的主靈敏度系數較大，軸向力加載對其他2個分量(VN為法向力分量，VMz為俯仰力矩分量)的干擾很小。

軸向力加載時各分量的輸出電壓隨加載載荷的變化如圖3所示，可見壓電天平結構響應的線性特性顯著。采用類似方法對法向力和俯仰力矩的測量靈敏度進行評估，結果表明：天平整體的結構響應線性特性顯著。

綜合加載用于評估天平整體性能。在綜合加載驗證中，在加載點同時施加350 N的軸向力、150 N的法向力和1 N·m的俯仰力矩。從各分量輸出電壓(表3)可以看出，綜合加載的輸出為各分量單獨加載的輸出之和，這也說明采用單獨加載的方案能夠實現天平靈敏度的評估。

表2 軸向力加載時各分量的輸出電壓Table 2 Balance output voltage with different axial force loads

圖3 各分量輸出電壓隨加載載荷的變化

表3 綜合加載時天平各分量的輸出電壓Table 3 Balance output voltage with composite load

在實際使用中，壓電天平測量得到的是壓電片上的電荷輸出量，而不是電壓輸出量。為實現與真實校準結果的對比分析，本文將ANSYS評估得到的天平的電壓靈敏度系數通過下式轉變為電荷靈敏度系數[3]：

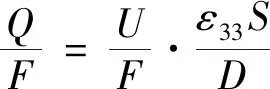
(12)

其中，ε33為PZT壓電陶瓷的Z向介電常數，Q為電荷輸出量，U為電壓輸出值，F為力載荷，S為壓電陶瓷片的面積，D為壓電陶瓷片的厚度。

從靜力分析得到的天平的電荷靈敏度系數(表4)可以看出：壓電天平各分量具有較高的主靈敏度系數和較小的干擾靈敏度系數，天平具有較強的抗干擾能力。

表4 天平靈敏度評估結果Table 4 Simulation results of the balance sensitivity

3.4 瞬態響應特性分析

對壓電天平進行了瞬態加載過程的模擬，以研究其動力學特性。動力學分析的加載過程分為2個階段：前0.005 s為載荷為0的階段；從0.005 s開始施加階躍載荷，模擬突然加載的過程，考察天平對階躍載荷的響應特性，時間間隔為0.0001 s。加載曲線如圖4所示。

圖4 動力學分析加載過程

動力學分析為綜合模擬，加載的載荷為軸向力350 N、法向力150 N、俯仰力矩1 N·m。計算加載過程中天平各分量的電壓輸出情況。在動力學分析中，對加速度計的輸出特性也進行了模擬，圖5為使用加速度計慣性補償前后的天平法向力的輸出電壓曲線。

圖5 法向力輸出補償結果

動力學分析的結果表明：進行慣性補償后，天平輸出信號平直段的信號大小與靜力分析的結果一致。法向力分量和俯仰力矩分量的補償效果類似，而軸向力分量的頻響較高，這也與試驗結果一致。風洞試驗中，對于法向力分量和俯仰力矩分量，在風洞有效試驗時間內，天平一階振動得不到完全阻尼，天平輸出的是多種頻率的振動信號和有效試驗信號的疊加信號，必須使用加速度計對振動信號進行補償，才能在試驗中得到可靠的氣動力數據。從圖5可以看出，使用加速度計可以對振動信號進行補償，但在補償過程中，又將加速度計的高頻振動信號引入了試驗信號中。在實際使用中，需要采用濾波方法濾除加速度計的高頻振動信號，再對試驗信號進行補償。

4 天平校準和風洞試驗結果分析

4.1 天平校準結果

壓電天平制作完成后，采用單分量校準的方式進行了靜態校準，即保持其他分量為常量，每次只校準一個分量。壓電天平靜態校準結果見表5。

表5 天平校準結果Table 5 Balance calibration results

對比表4和表5，可以看出：對于天平各分量的主靈敏度系數，天平校準結果比ANSYS模擬結果小12%左右。其主要原因是：在ANSYS模擬時，考慮的是一種理想狀態，壓電陶瓷片厚度采用名義值0.5 mm，但其實際厚度與名義值存在差異；另外，也未考慮壓電片陶瓷片與力敏梁之間環氧樹脂膠層的影響(因其厚度無法測量)，從而造成天平校準得到的主靈敏度系數小于模擬得到的結果。

但天平的干擾靈敏度系數均遠大于模擬得到的結果，某些分量間的干擾靈敏度系數存在量級差別。其主要原因是：(1) 配對使用的壓電陶瓷片的性能不完全一致，各分量間的干擾不能通過壓電陶瓷片的極性選擇完全抵消；(2) 加工和校準天平時，力敏梁的結構對稱性和天平安裝位置存在誤差。但在實際校準中，天平的干擾靈敏度系數是小量，因此，使用ANSYS有限元分析軟件預估壓電天平的性能是有效的。

4.2 風洞試驗結果

為了檢驗天平的性能，在0.6 m激波風洞上進行了APOLLO模型測力驗證試驗。圖6為天平法向力、加速度計、慣性補償后的法向力以及皮托壓力輸出曲線。從圖中可以看出：使用加速計進行補償后，可以明顯去除法向力輸出信號中的低頻分量，這與模擬結果一致。經過加速度計補償后的法向力輸出曲線與皮托壓力輸出曲線有很好的跟隨性。在風洞試驗中，加速度計的一階振動頻率與模擬結果不一致，這主要是因為連接支桿的存在以及模型質量的影響，導致系統振動頻率降低。

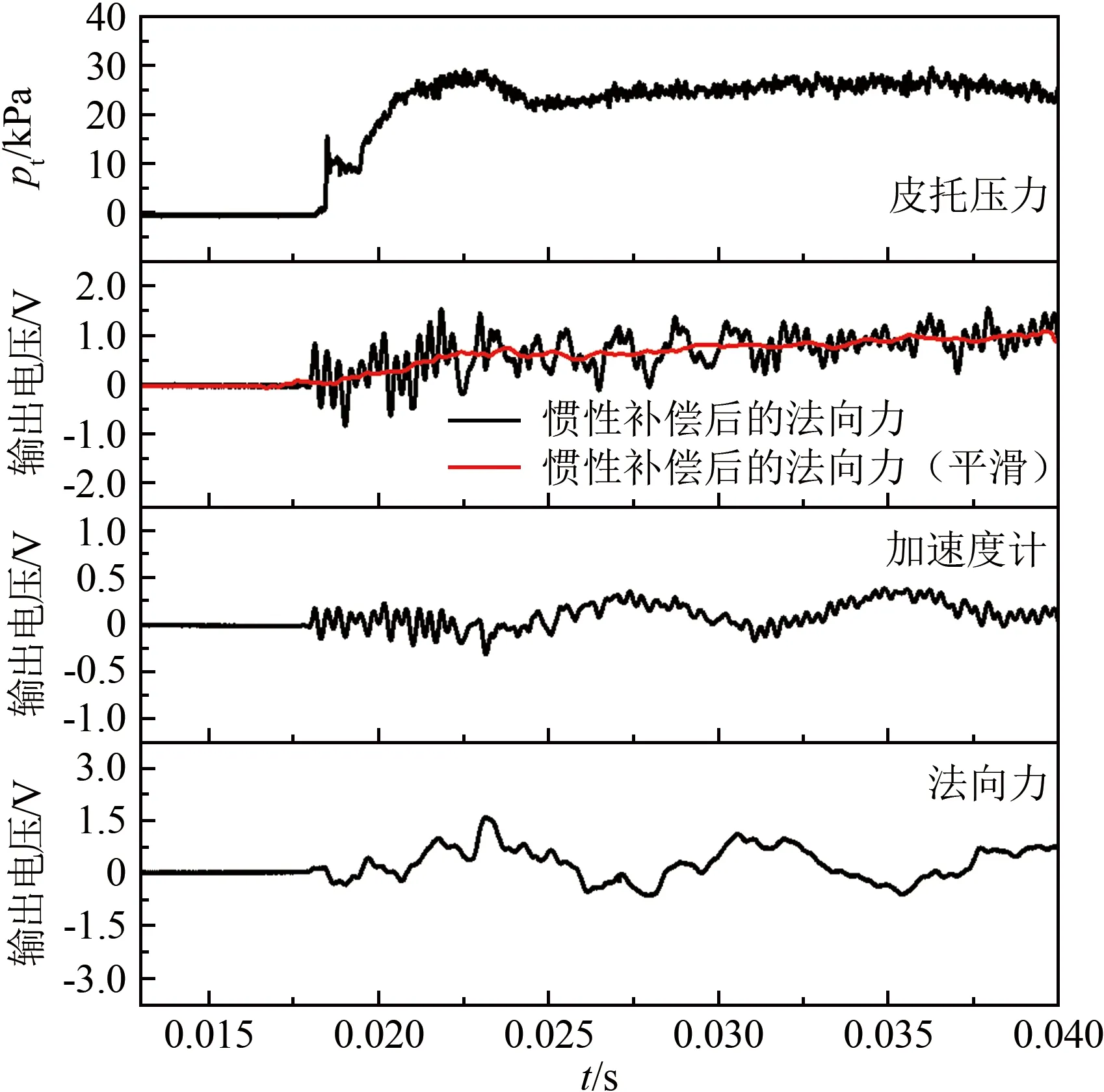
圖6 法向力試驗輸出信號

5 結 論

利用ANSYS力電耦合的有限元分析方法，對一臺三分量壓電天平的性能進行了評估，并與天平實際校準結果進行了對比，得到如下結論：

(1) 靜力學分析的結果表明，設計的三分量壓電天平具有較好的線性特征，天平的主靈敏度系數較高，抗分量間干擾的效果較好。

(2) 模態分析的結果表明，天平的頻響較高，通過加速度計對天平的一階振動干擾進行補償后，可以滿足激波風洞毫秒級測力試驗需求。

(3) 瞬態動力學過程分析能夠評估壓電天平的動態特性以及加速度計慣性補償方案的有效性。

本文將ANSYS應用于壓電天平設計，可以在設計階段評估天平性能，達到為天平設計服務的目的。