工作面運輸平巷超前支護技術優化研究
姜明偉 王子君 戴星航 陳忠越
(遼寧石油化工大學礦業工程學院,遼寧省撫順市,113001)
采煤工作面運輸平巷擔負著工作面煤炭運輸、通風、行人等重要任務,因此保證工作面運輸平巷的支護效果對工作面安全高效開采尤為重要,工作面運輸平巷的穩定性是工作面安全高效開采的前提。隨著采煤工作面的推進,工作面圍巖穩定結構遭到破壞,巷道圍巖應力重新分布,在工作面前方的一定區域內形成超前支承壓力[1-3]。工作面前方的運輸平巷處于超前支承壓力輻射范圍內[4],加之上覆巖層自重應力的影響,工作面運輸平巷會出現頂板下沉量過大、片幫等問題,嚴重影響了工作面正常開采。
在使用邁步式液壓支架之前,工作面運輸平巷多采用錨桿、錨索、單體液壓支柱配合金屬鉸接頂梁支護方式[5]。20世紀90年代初,兗礦集團設計并開發出了履帶式超前支架[6];2014年,盧進南等為解決超前支護問題,設計了液壓邁步式超前支護裝備[7]。目前,巷道超前支護支架主要是液壓支架為基礎的四連桿機構和移動的單元循環式超前支架兩大類[8-9]。考慮到邁步式超前支護液壓支架在煤礦應用已經相當廣泛,但很少有學者分析邁步式液壓支架與單體液壓支柱支護在控制巷道圍巖變形上的差異,因此本文就邁步式超前支護液壓支架與單體液壓支柱支護效果進行對比分析,用巷道圍巖變形量和頂板位移速率兩個主要參數的數值模擬結果為兩種超前支護方式選擇提供定量依據。
1 工作面運輸平巷變形機理
工作面運輸平巷變形主要有3種影響因素。
(1)傾斜方向應力集中。當運輸平巷臨近采空區時,由于上一個工作面開采形成采空區,下一工作面的運輸平巷正處于上一工作面開采形成的傾斜應力集中范圍內,導致平巷壓力增大。
(2)運輸平巷掘進本身影響。隨著巷道掘進,原本穩定的應力場被破壞,應力重新分布,在一定范圍內巷道的應力集中增大,巷道產生變形。
(3)工作面開采的二次采動影響。隨著工作面向前推進,上覆基本頂出現離層、斷裂、整體下沉,工作面支架受力增大形成老頂初次來壓,直接頂懸露一定程度后開始發生斷裂并垮落[10],形成周期來壓,如圖1所示。由關鍵層理論[11-12]分析可知:支架的工作狀態對頂板支護效果有較大的影響,當支架梁產生大的彎曲時,梁與頂板的接觸點到梁端的距離增大,此時容易發生冒頂事故。由于形成的是半拱形結構,工作面一側的運輸平巷正處于這一影響范圍內,所以工作面運輸平巷前方一定區域內將承受很大的應力,這時運輸平巷承受應力迅速增大,導致頂板下沉、兩幫片幫,嚴重影響工作面的正常開采。
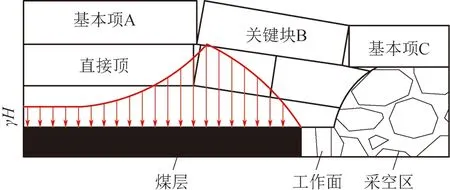
圖1 采動支承壓力分布圖
2 數值模擬與模擬結果分析
2.1 工程背景
山西煤炭運銷集團四通煤業有限公司北二采區205工作面主采2#煤層,煤層傾角3°~7°,平均傾角5°,埋深600 m,煤層平均厚度3.2 m,其硬度f=2~3。直接頂為泥巖,平均厚度5 m;老頂為細砂巖,平均厚度19.2 m;直接底板為中砂巖,比較堅硬,平均厚度4.8 m。205工作面為綜采工作面,采用走向長壁后退式采煤法。
2.2 數值模型的建立
建立工作面運輸平巷數值模型,X方向為40 m,Y方向為100 m,Z方向為40 m,運輸平巷寬度為4 m,高3.2 m。平巷右側留20 m保護煤柱,平巷全長32 m,采空區8 m,模擬自重應力為15 MPa,具體模擬參數如表1所示,模型采用庫倫-摩爾模型計算[13]。

表1 模型參數
巷道兩幫各打3根錨桿,頂板5根錨桿,錨桿長度2 m,錨桿間距為0.8 m,頂板有1排錨索,錨索長度為8 m,錨索間距0.8 m。
(1)方案一:采用單體液壓支柱支護,整條巷道放置2排單體液壓支柱,2排支柱分別距煤壁0.8 m,支柱間距為1 m,利用樁單元模擬單體液壓支柱,模擬狀況如圖2所示。

圖2 單體支柱數值模擬
(2)方案二:采用邁步式超前支護液壓支架支護,整條巷道放置3組邁步式超前支護液壓支架,前后兩組支架距離為2 m,支架一側留0.8 m行人通道,用樁單元和梁單元模擬邁步式液壓支架的頂梁和立柱,模擬狀況如圖3所示。樁單元和梁單元力學參數如表2所示。
為體現模擬開挖過程與實際生產的一致性,對工作面開采進行分步模擬,工作面每向前開挖1.6 m,在模型中運行5000步,每次開挖后給采空區賦內聚力較小的模型參數,共開挖20次。
在進行兩種支護方式模擬時,在工作面運輸平巷距離工作面30 m處設置觀測斷面,每個觀測斷面取5個代表性的觀測點,觀測點具體位置如圖4所示。

圖3 邁步式支架數值模擬

表2 樁單元和梁單元力學參數
工作面每向前推進1.6 m計算一次巷道位移,分別記錄工作面距觀測點30 m、25 m、20 m、15 m、10 m時觀測點位移變化情況。
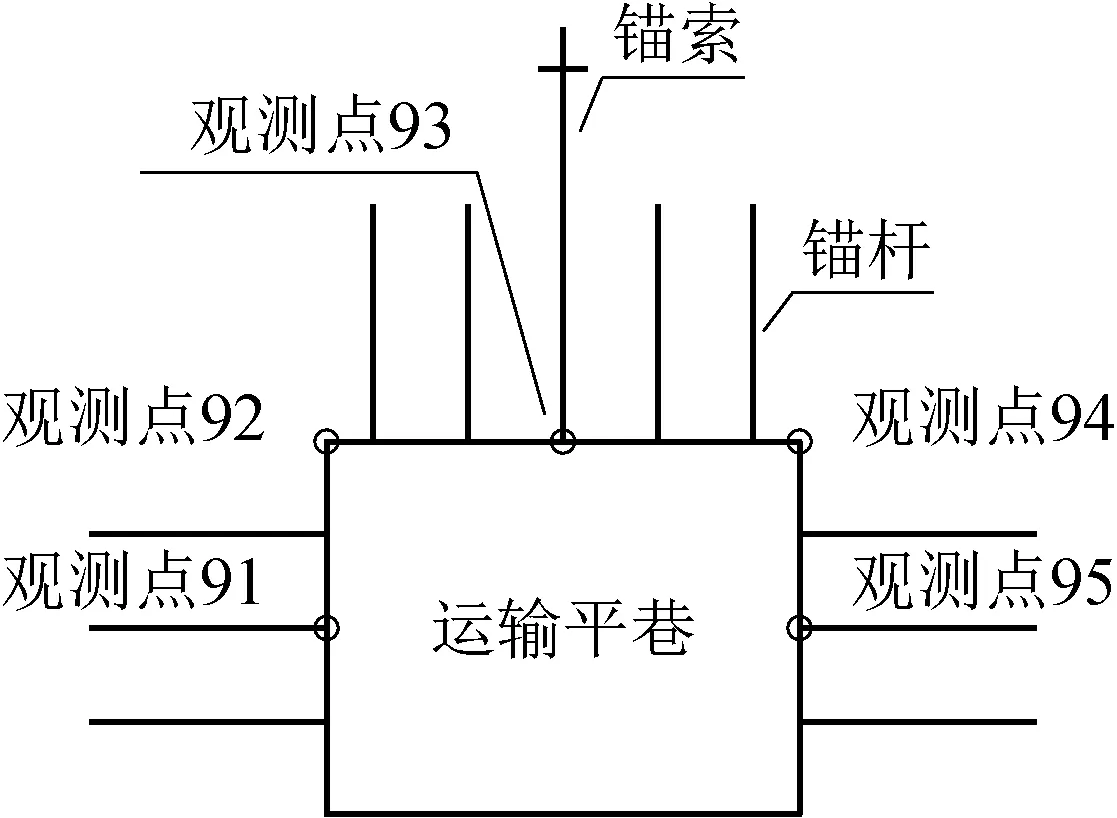
圖4 數據采集點位置
2.3 巷道圍巖變形量分析
利用前述的數值模型模擬205工作面采動對工作面運輸平巷變形量的影響,兩種支護方式在不同位置巷道變形量如圖5所示,可以看出:
(1)兩種支護方式巷道位移曲線都呈單峰值狀態,即在巷道中間位置變形量最大,兩角點次之,兩幫變形量最小。由于靠近煤壁一側巷道受采動影響較大,因此靠近煤壁一側角點和腰線處位移要略大于遠離煤壁一側;
(2)隨著開采位置逐漸靠近觀測點,巷道整體位移量也逐漸變大,在開采到觀測點附近時,兩種支護方式位移量都達到峰值;

圖5 巷道圍巖形變量對比
(3)無論工作面開采至任何位置,邁步式液壓支架的支護效果都明顯好于單體液壓支柱,不同位置最大位移差值見表3。從表3可以看出,使用邁步式液壓支架和單體液壓支柱開采至不同位置最大位移量差值分別為70.4 mm、87.6 mm、111 mm、116.2 mm、197 mm,平均值為116.4 mm,因此采用邁步式液壓支架支護時的圍巖控制效果遠優于單體液壓支柱支護。

表3 不同位置最大位移差值
2.4 巷道圍巖變形速率分析
巷道的位移速率是影響巷道變形的一個重要指標,在短時間內形成有效的支護可以大大減少巷道變形量,使巷道保持穩定狀態。巷道圍巖變形速率模擬結果如圖6所示。
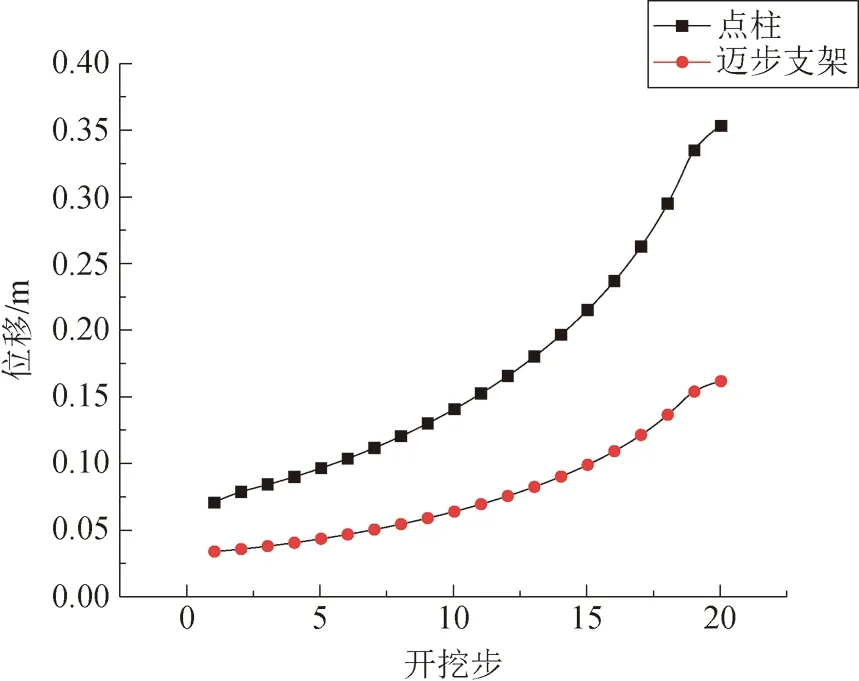
圖6 兩種支護方式下巷道位移速率對比
由圖6可以看出,隨著工作面的推進,受采動影響條件下兩種支護方式的巷道圍巖變形速率都呈上升趨勢,但采用邁步式支架支護方式要明顯小于單體液壓支柱支護。為進一步研究邁步式液壓支架與單體液壓支柱對巷道支護的位移速率,將位移曲線近似看成拋物線,考慮到樣本較少,可能存在偶然性,進行多次模擬并對各點取平均值,以保證參數的準確性,利用拋物線起點、中點、終點數值進行計算,各點取平均值如表4所示。

表4 兩種支護方式平均位移
由表4數據計算得到單體液壓支柱支護表達式為:
Y1=0.73X2-0.4X+71.07
(1)
邁步式液壓支架支護表達式為:
Y2=0.34X2-0.44X+34.31
(2)
式(1)和式(2)二次函數的一般表達式為:
Y=AX2+BX+C
(3)
由式(3)的基本性質可知,A決定了拋物線的開口方向和開口大小,根據計算公式可知A1/A2=2.15,因此使用單體液壓支柱支護巷道時的變形速率明顯高于邁步式液壓支架支護的變形速率,是邁步式液壓支架的2倍左右。邁步式液壓支架能有效控制巷道的位移變化,降低巷道圍巖的變形速率。
3 結論
(1)受工作面采動影響,工作面運輸平巷應力重新分布,在距工作面30 m范圍內,隨著開采的不斷推進,工作面運輸平巷變形量逐漸增大,并且巷道中間位置變形量最大,靠近煤壁一側巷道變形量略大于遠離煤壁一側的變形量。
(2)數值模擬結果表明,工作面運輸平巷采用邁步式液壓支架進行超前支護的支護效果明顯優于單體液壓支柱,頂板最大位移量平均相差116.4 mm。
(3)工作面運輸平巷采用單體液壓支柱進行超前支護,巷道圍巖變形速率是邁步式液壓支架支護時的2倍左右,邁步式液壓支架能在短時間內有效的控制巷道的變形,邁步式液壓支架更加適合工作面運輸平巷的超前支護。

