極大4限制邊連通圖的充分條件

郝海霞,張 磊,徐子鈞

(晉中學院數學學院,山西晉中030619)

所考慮的圖都是無向簡單圖。文中出現而未定義的概念和記號參見文獻[1]。設G=(V(G),E(G))是一個連通圖。用ν=|V(G) |表示G的階。若e=uv是G一條邊,則稱u與v相鄰。設S為G中的一個邊集,對于G中任意一點u,用N(u)表示在G中與u相鄰的點的集合,用d(u)表示在G中與u相鄰的點的數目。假設U是V(G)的一個非空子集。以U為頂點集,以G中兩個端點均在U中的所有的邊的集合為邊集所組成的子圖稱為G的由U導出的子圖,記為G[U];這時,也稱G[U]為G的導出子圖。圖G中的一條路是指一 個有限非空序列W=v0e1v1e2v2…ekvk,它的項交替地為頂點和邊,使得對 1 ≤i≤k,ei=vi-1vi,其中v0,v1,v2,…,vk-1,vk互不相同。稱W是從v0到vk的一條路, 此時, 若v0=vk,則稱W為G中的圈。W中邊的數目稱為W的長。長為k的路(或圈)稱為k-路(或k-圈)。G的圍長g(G)是指G中最短圈的長。若在G中頂點u和v是連通的,則u和v之間的距離d(u,v)是G中最短(u,v)-路的長。V1,V2是V(G)的非空子集V1,V2之間的距離定義為d(V1,V2)= min{d(u,v):u∈V1,v∈V2}。稱滿足d(V1,V2)=k的點集對V1,V2是k-距離極大的, 如果不存在頂點子集滿 足使得對G的兩個非空頂點子集X與Y,用[X,Y]表示G中一端點在X中另一端點在Y中的所有邊組成的集合,X是V(G)的非空子集,G的邊割是指形為[X,Y]的E(G)的子集,其中Y=V(G)X。

多處理機的互連網絡拓撲常以圖為數學模型,用圖的頂點(即節點)代表處理機,用邊來代表處理機之間的直接通信聯系,因此網絡拓撲的性能可以通過圖的性能和參數來衡量。為系統設計或者選擇網絡拓撲時,一個基本的考慮是系統的可靠性,它對應圖的連通性。但是用邊連通度來研究系統的可靠性不夠精確。在此背景下,1996 年FAbrega和Foil在文獻[2]中提出了k限制邊連通度的概念。

定義1設G是一個連通圖,S?E(G)是G的一個邊割。如果G-S的每個連通分支至少有k個頂點,那么稱S是G的一個k限制邊割。

稱G的所有k限制邊割中所含邊數最少的邊割為G的λk-割,λk-割所含的邊數稱為G的k限制邊連通度,記為λk(G)。當k=2 時,通常稱k限制邊連通度為限制邊連通度, 記為λ′(G)。應該指出,不是所有圖都存在k限制邊割。若G存在k限制邊割,則稱G為λk-連通圖。近年來,對于一般的正整數k,k限制邊連通度得到了廣泛的研究,見文獻［3-5］。從目前的研究結果來看,對于連通圖G,人們相信λk(G)越大,G所對應的網絡的可靠性就越好［6-8〕,因此人們希望圖G的k限制邊連通度盡可能地大。顯然這需要λk(G)的一個上界。對正整數k,定義ξk(G)=min{[X,Y]:|X|=k,G[X]連通,Y=V(G)X}。

若λk(G)=ξk(G),則稱G是極大k限制邊連通的。

將給出極大4限制邊連通圖與圍長和3-距離極大點集對的關系。

引理 1設G是λ4-連通圖。若ν(G)≥11, 則λ4(G)≤ξ4(G)［9］。

引理2令G是一個滿足λk(G)≤ξk(G)的λk-連通圖且[X,Y]是G的一個λk-割。若G[X]中存在一個k階連通子圖H滿足

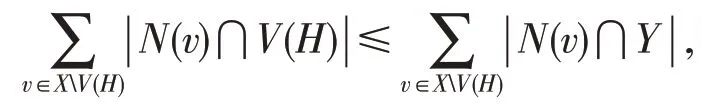
則G是極大k限制邊連通的[10]。

定理1設G是一個階ν(G)≥11 的λ4-連通圖。若G的圍長g＞6 且對于G中任意3-距離極大點集對S,T,在G[S∪T]中都有階為4 的連通分支,則G是極大4限制邊連通的。

證明用反證法。假設G不是極大4 限制邊連通 的 。 因 為ν(G)≥11,由 引 理 2.1,所 以λ4(G)≤ξ4(G)。 則λ4(G)＜ξ4(G)。設 [X,Y]是G的λ4-割。若 |X|=4 或 |Y|=4, 則有ξ4(G)≤| [X,Y] |=λ4(G), 矛盾。 故 |X|≥ 5 且 |Y|≥5 。設X1?X,Y1?Y是與[X,Y]中至少一條邊相關聯的點集。令X0=XX1,,Y0=YY1。

斷言X0≠φ且Y0≠φ。

假設X0=φ, 則X1=X, 即對任意的u∈X有|N(u)∩Y|≥1。由于|X|≥5, 因此在G[X]中存在 一個4 階連通子圖H0。因為g＞6,所以對于任意的u∈XV(H0)有|N(u)∩V(H0)|≤1。故我們有

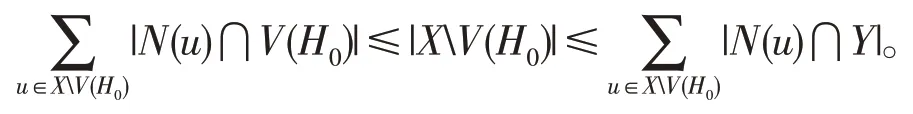
由引理2知,G是極大4限制邊連通的,矛盾。

同理可得Y0≠φ。斷言證明完成。

由于d(X0,Y0)≥3, 因此G中存在一個3-距離極大點集對S,T,使得X0?S且Y0?T。由題設知,在G[S∪T]中存在階為4的連通分支H。由于G的圍長g＞6,因此H為一條3-路或者同構于K1,3,且對于任意的u∈V(G)V(H)有

令V(H)={w0,w1,w2,w3}。由于G的圍長g＞6,因此

其中 0 ≤i,j≤ 3,i≠j。

因為H是G[S∪T]中的連通分支,所以對于任意u∈(X0∪Y0)V(H), 都有 |N(u)∩V(H)|=0 。此時,對 于任意 的v∈V(H), 有N(v)V(H)?X1∪Y1。 由X,Y的對稱性, 下面考慮 |V(H)∩X|≥|V(H)∩Y|的情形。

情形1|V(H)∩X|=4。

注 意 到 對 于 任 意u∈(X0∪Y0)V(H), 都 有|N(u)∩V(H)|=0。結合(1)式,對于XV(H)中任意一點x,都有|N(x)∩V(H)|≤|N(x)∩Y|。因此我們有

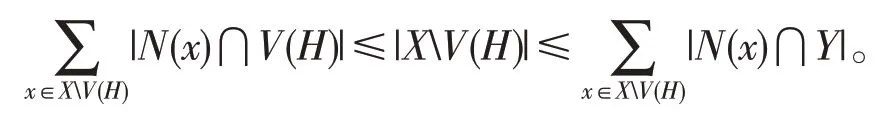
由引理2知,G是極大4限制邊連通的,矛盾。

情形2|V(H)∩X|=3。

（1）H是一條3-路。

不妨設H=w0w1w2w3。因 |V(H)∩X|=3 所以|V(H)∩Y|=1。

|{w0,w3}∩X|=1。

由對稱性,我們不妨設w0∈X。因為|V(H)∩X|=3,所以w0,w1,w2∈X。由于G的圍長g＞6,因此 (N(w0)∪N(w1)∪N(w2))∩X1中的點與N(w3)∩Y1中的點不相鄰。結合(2)式,我們有

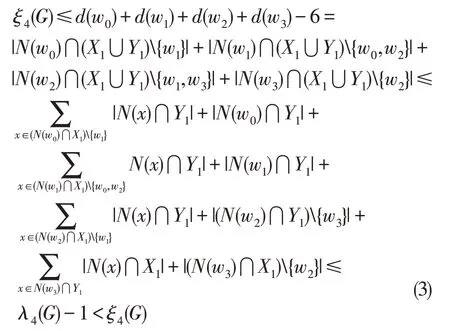
矛盾。

|{w1,w2}∩X|=1。

由對稱性, 我們不妨設w1∈X。因為|V(P)∩X|=3, 所以w0,w1,w3∈X。由于G的圍長g＞ 6, 因此 (N(w0)∪N(w1)∪N(w3))∩X1中的點與N(w2)∩Y1中的點不相鄰。因為w1w2,w2w3∈[X,Y], 結合(2)式和(3)式,所以我們有

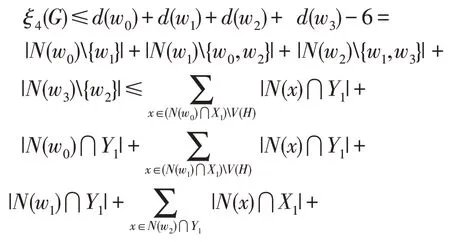
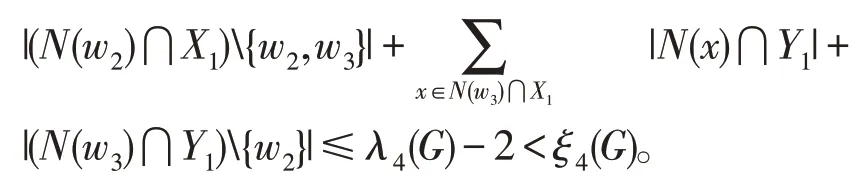
（2）H?K1,3。

不妨設dH(w0)=3。

|{w1,w2,w3}∩X|=2。

由對稱性, 我們不妨設w3∈Y。因為 |V(H)∩X|=3,所以w0,w1,w2∈X。由于G的圍長g＞ 6,因此 (N(w0)∪N(w1)∪N(w2))∩X1中的點與N(w3)∩Y1中的點不相鄰。因為w0w3∈[X,Y],結合(2)式和(3)式,所以我們有

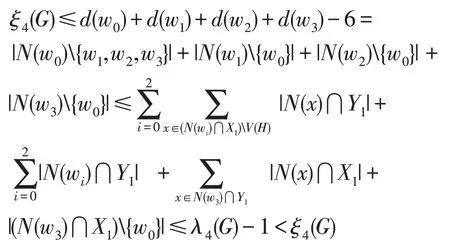
矛盾。

w0∈Y。

因為 |V(H)∩X|=3, 所以w1,w2,w3∈X。由于G的圍長g＞6, 因此 (N(w1)∪N(w2)∪N(w3))∩X1中的點與N(w0)∩Y1中的點不相鄰。因為w0w1,w0w2,w0w3∈[X,Y], 結合(2)式和(3)式,所以我們有

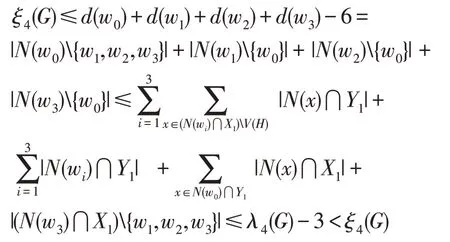
矛盾。

情形3|V(H)∩X|=2。

（1）H是一條3-路。

不妨設H=w0w1w2w3。因為 |V(H)∩X|=2, 所以|V(H)∩Y|=2。

（2）|{w0,w3}∩X|=1。

由對稱性,我們不妨設w0∈X。因為V(H)∩|X|=2,所以w0,w1∈X或w0,w2∈X。由于G的圍長g＞ 6,因此當w0,w1∈X時, (N(w0)∪N(w1))∩X1中的點與N(w2)∪N(w3)∩Y1中的點不相鄰。注意到w1,w2∈[X,Y]。結合(2)式和(3)式,我們有

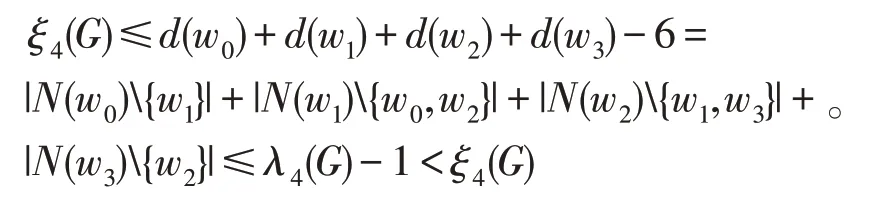
矛盾。

當w0,w2∈X時,由 于G的 圍 長g＞6,因 此(N(w0)∪N(w2))∩X1中的點與N(w1)∪N(w3)∩Y1中的點不相鄰。注意到w0w1,w1w2,w2w3∈[X,Y]。結合⑵式和(3)式,我們有

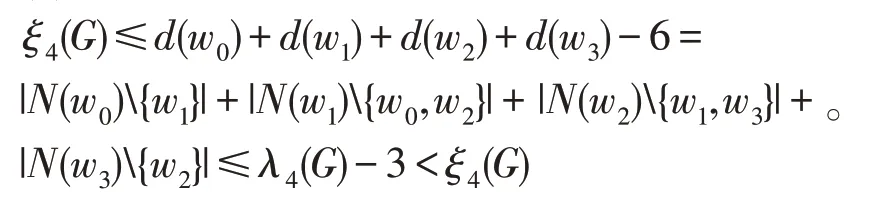
矛盾。

|{w0,w3}∩X|=0

或|{w0,w3}∩X|=2。

由對稱性, 我們不妨設|{w0,w3}∩X|=0。因為|V(H)∩X|=2,所以w1,w2∈X。由于G的圍長g＞6,因此N(w1)∪N(w2)∩X1中的點與 (N(w0)∪N(w3))∩Y1中的點不相鄰。注意到w0w1,w2w3∈[X,Y]。結合⑵式和(3)式,我們有

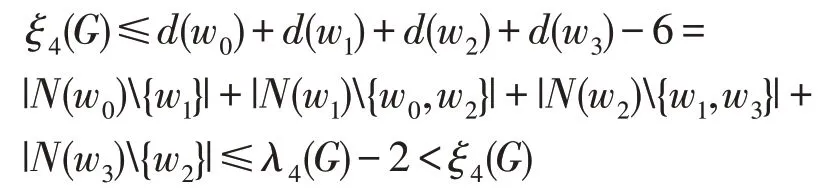
矛盾。

2H?K1,3。

不妨設dH(w0)=3 。因為 |V(H)∩X|=2, 所以|{w1,w2,w3}∩X|=2 或|{w1,w2,w3}∩Y|=2。由對稱性,我們 不 妨設 |{w1,w2,w3}∩X|=2 且w3∈Y。易 知w1,w2∈X且w0∈Y。 由 于G的圍 長g＞ 6, 因 此(N(w1)∪N(w2))∩X1中的點與 (N(w0)∪N(w3))∩Y1中的點不相鄰。注意到w0w1,w0w2∈[X,Y]。

結合⑵式和(3)式,我們有

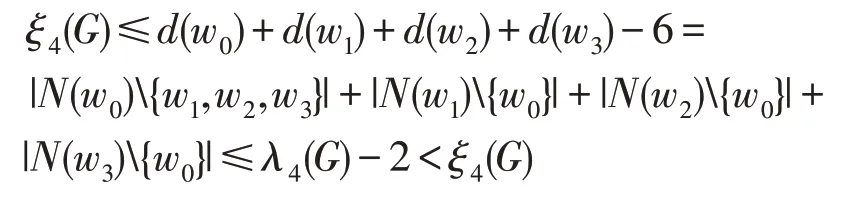
矛盾。