基于機器學習的個人信用模型實證分析

張 暉，張志明

銅陵學院金融學院，安徽銅陵，244061

1 引 言

隨著信息技術的高速發展和互聯網的普及，征信領域發生了巨大的變化。大數據征信逐漸開始取代傳統征信模式。傳統征信數據來源單一，主要以傳統商業銀行的違約記錄作為征信依據，覆蓋人群范圍較小，不能準確判斷個人實際征信狀況。大數據征信以互聯網為平臺，采用數據抓取和數據挖掘技術，運用合理的算法判斷個人或企業的信用狀況。其數據種類多樣，來源廣泛，具備綜合判斷的能力。近年來，個人信用模型不斷完善，從早期的判別分析模型到今天的基于機器學習的個人征信模型層出不窮。本文通過P2P平臺，在經過用戶允許的情況下，采集1 000名用戶的個人信息，運用四種不同的機器學習方法進行對比，將數據按照7∶3比例劃分，70%數據用于訓練，30%數據用于驗證模型，分析在有限數據情況下不同算法的準確度。

2 個人征信模型發展綜述

個人征信模型是以評分對象過去的社會經歷和交易記錄為數據，采用數理統計的方法，分析和判斷個人的信用狀況。1941年，Durand在其編寫的《消費者分期付款信貸的風險因素》一書中，提出了數理統計模型用于消費者授信決策的統計方法［1］。1958年，Fair等利用判別分析法建立了第一個真正現代意義上的商業化信用評分系統FICO，其產品在商業金融領域迅速得到了廣泛應用［2］。

計算機和信息技術的發展提高了個人征信模型的數據處理能力。在互聯網時代，個人征信的數據來源海量增長，機器學習的方法有助于處理大數據性質的征信數據。基于機器學習的個人征信模型的核心是通過搜集和挖據互聯網以及其他平臺的數據，把人類的經驗通過訓練的方式讓機器進行學習，經過反復檢驗后得出正確率高的算法或模型，用于預測個人違約概率。

近幾十年來，機器學習算法層出不窮。1967年，Cover和 Hart提出了 KNN算法（臨近算法）［3］。其全稱為K-Nearest Neighbor，意思是K個最靠近的鄰居。20世紀80年代，Breiman等人發明了決策樹算法，通過反復二分數據進行分類或回歸，大大降低了計算量［4］。2001年，Breiman在決策樹的基礎上提出了隨機森林算法，利用多棵樹對樣本進行訓練和預測［5］。樸素貝葉斯分類器（Naive Bayes Classifier，或NBC）發源于古典數學理論，有著堅實的數學基礎以及穩定的分類效率。同時樸素貝葉斯模型所需估計的參數很少，對缺失數據不太敏感，算法也比較簡單［6］。從理論上來看，樸素貝葉斯模型與其他方法相比誤差較小，但由于假設條件嚴格，現實中往往并不成立。1995年，Vapnik等人對線性分類器提出了另一種假設，即支持向量機（Support Vector Machine，簡稱SVM），其核心思想是尋找一個超平面把數據集的樣本空間劃分成不同的樣本用于分析判斷［7］。

綜上所述，可以看出當前機器學習數據處理方法取得了諸多的成果，并運用到了個人征信領域中。如美國金融科技公司ZestFinance的個人信用評分模型，從3 500個數據項提取70 000個變量，利用10個預測分析模型進行訓練和學習，從而分析消費者的信用狀況［8］。國內支付寶旗下的芝麻信用以及騰訊金融、京東金融等互聯網金融平臺也都紛紛建立了自己的信用評分體系。

3 實證分析

3.1 數據描述

本文數據來源于P2P平臺貸款客戶資料，變量指標共14項，分別為“年齡”“職業”“收入”“婚姻狀況”“教育程度”“存款”“房產”“車輛”“網購消費金額”“債務余額”“違法記錄”“公積金”“支付寶年齡”“違約記錄”。

3.2 數據處理

上述征信數據中，既有文本型數據，也有數字數據，原始數據無法直接適用于評估模型。同時，數據中的連續變量可能造成數據之間不同的區分度，因此需要對連續變量做進一步編碼，使得編碼后的數據能夠充分反映變量的變化，可以被模型充分學習。

年齡變量是一個連續型變量，其數值對客戶信用可能呈“U型”分布，即在年齡數值較小時或較大時對客戶可信度具有負作用，中間數值呈正作用［9］。因此直接使用數據作為判斷依據，可能對線性模型的評估帶來障礙，需要對數據進行重新編碼。針對年齡變量，以5歲為一個階段劃分區間，將年齡數據分為：（0，15］、（15，20］、（20，25］、（25，30］、（30，35］、（35，40］、（40，45］、（45，50］、（50，55］、（55，60］、（60，65］、（65，70］，共12個區間。通過重新編碼，將年齡1維數據轉換成12維數據，讓模型避免“U型”難點。經過重新編碼后部分結果如表1所示。

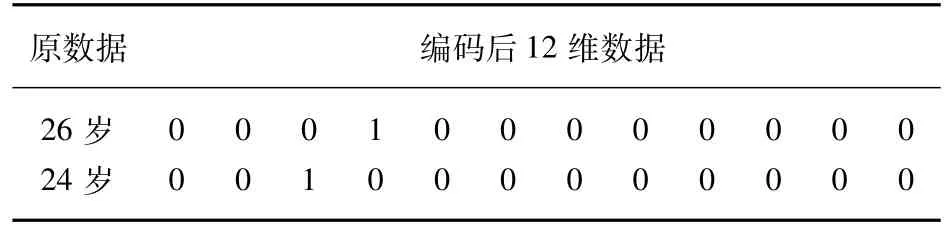
表1 年齡變量數據處理

收入數據按照2017年個人所得稅征稅級距為梯度劃分。收入數據雖然不存在“U型”數據難點，但是工資的額度增加不一定與信用評分呈線性關系，因此需要對工資進行再編碼，使工資變換能夠被分類器學習，并將收入映射到梯度區間。但是，由于其數值較大，可能會帶來因數據單位不一致帶來的參數變化，使得模型泛化能力較低，因此對其取以2為底的對數。一方面可以反映數據的變化趨勢，另一方面可壓縮數值，避免因為數據變化造成模型的效果差。與年齡不同的是，工資的每個階段都有實質作用，因此需要記錄每個階段的數值，處理后部分結果如表2所示。

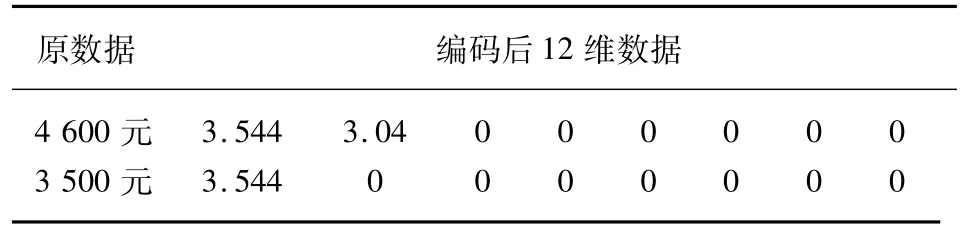
表2 收入變量數據處理

職業劃分按照商業銀行個人信用評估的一般標準，劃分為無職業、個體、教師、醫護人員、職員、公務員和金融從業者。其中職員又可分為初級職員、中級職員和高級職員。在職員部分做進一步編碼如表3所示。

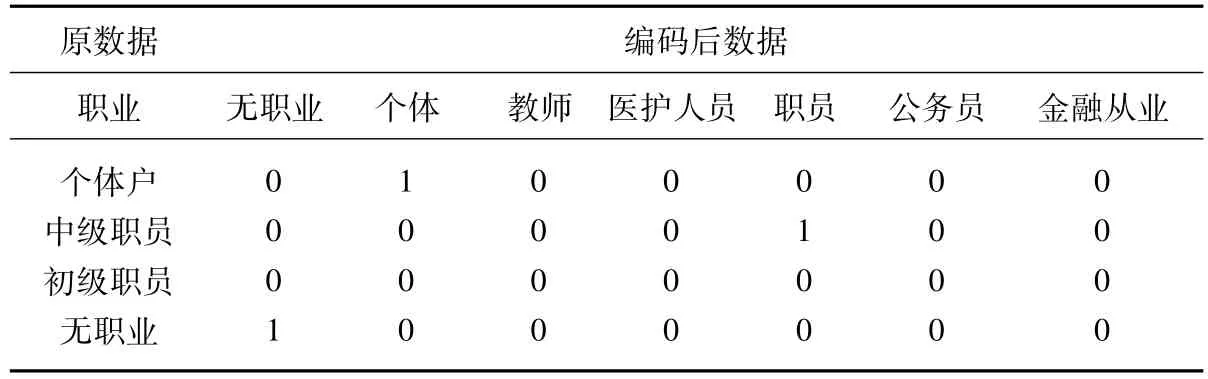
表3 職業變量數據處理

網購消費金額一般數值較大，通過對其進行標準化數據壓縮，將原始數據映射到［0，1］區間，避免因數據數值過大帶來的模型誤差，部分結果見表4。

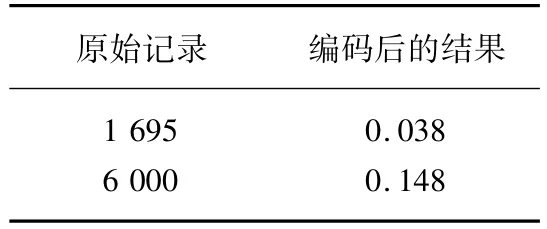
表4 網購消費金額變量處理

存款數據數額較大，在處理上對其以2為底取對數，進行壓縮，部分結果如表5所示。

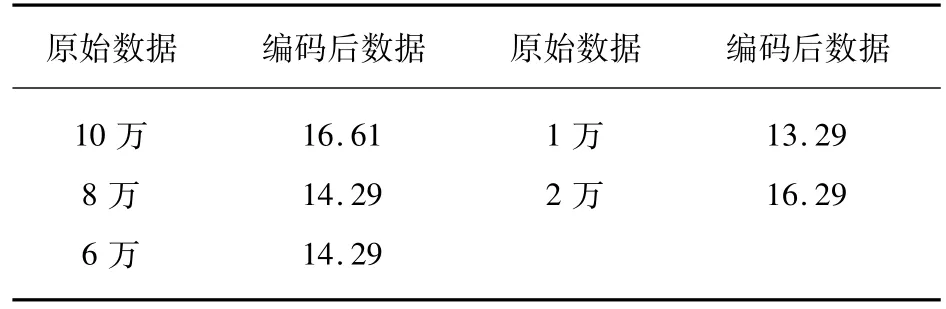
表5 存款數據變量處理

教育程度范圍大致可分為，小學、初中、高中、本科、碩士、博士。受教育程度是一種遞進關系，適合使用連續編碼方式表示，處理結果如表6所示。

表6 教育程度變量處理

債務余額記錄可分為：房貸、車貸和其他貸款。原始數據中有很多數據表示不明，無法確認具體貸款額度，所以在操作中將其標記為是否有該項貸款，確認貸款信息，部分結果如表7所示。

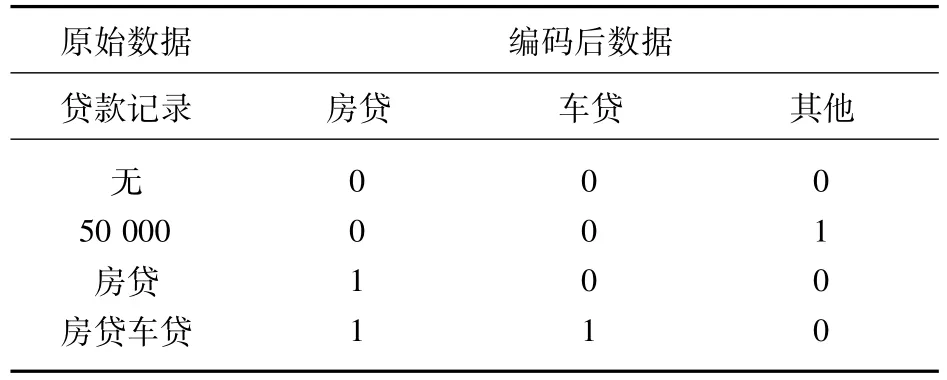
表7 債務余額變量處理

房產、車輛、公積金信息根據有無劃分為1、0，婚姻狀態未婚為0，已婚為1，離異為2；支付寶年限可以直接使用。

3.3 模型選擇

分別選用SVM、決策樹、隨機森林、樸素貝葉斯進行個人信用數據分析，對比不同模型的分析結果。

SVM本質上是針對線性可分情況進行分析，通過設置軟間隔距離，保證了分類的泛化性，降低過擬合情況。當分類特征是非線性時，通過非線性映射算法，將低維非線性特征映射成高維空間乃至無窮維，使其線性可分。從而使得利用線性分割法完成對非線性空間的劃分［10］。方案使用高斯核函數將輸入向量映射到高緯空間，借助網格搜索法，調節“軟間隔”距離，選擇最優訓練模型。

決策樹主要包括ID3，C4.5和CART。信息增益是ID3的分裂標準，它定義了一個特征的信息量：攜帶的信息越大，該特征在分裂篩選過程中權重越大。實踐發現：以信息增益為分裂標準時，分裂過程中偏向于選擇數據種類較多的分類屬性。C4.5將信息增益率作為劃分標準，優化了ID3弊端，但仍舊難以避免決策樹中結構復雜、規模大、運行效率低等問題。CART使用GINI系數，在前人的基礎上，降低了決策樹復雜性，提高決策樹算法執行效率［11］。方案使用CART算法，以單個最小節點為2個樣本點為分割終止點，對分類器進行評價。

隨機森林從bootstrap重采樣法等角度，構建集成決策樹可緩解上述問題。本方案通過使用35棵CART決策樹，以GINI系數為分割依據。通過網格化自動搜索，不同的分割深度、最小分割樣本點數等參數，選擇最優訓練模型。

樸素貝葉斯方法是基于貝葉斯定理的一組有監督學習算法，即“簡單”地假設每對特征之間相互獨立。盡管其假設過于簡單，在很多實際情況下，樸素貝葉斯工作得很好，特別是文檔分類和垃圾郵件過濾等數據量大，特征稀疏的分類環境。方案使用服從多項分布數據的樸素貝葉斯算法，將alpha平滑因子設置為1進行分類。

采用Pyhton3.6.0軟件，根據常規搜索算法調整模型參數，將數據隨機分成訓練數據和測試數據兩份，比例為7∶3。訓練數據用于訓練模型，測試數據用于對模型進行評價。評價指標主要包括準確率、召回率和F1值。準確率是評估捕獲的成果中目標成果所占得比例；召回率是從關注領域中召回目標類別的比例；F1值則是綜合這二者指標的評估指標，用于綜合反映整體的指標。結果如表8所示。

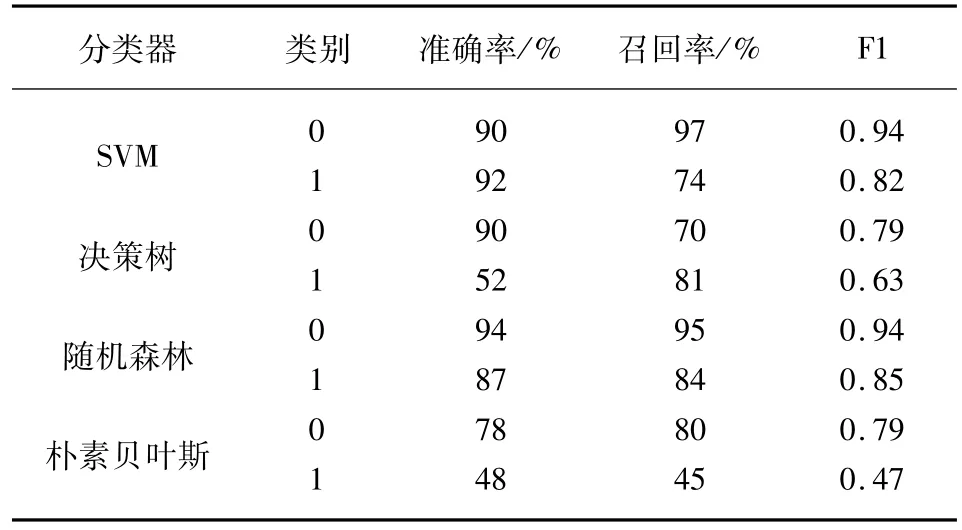
表8 機器學習個人征信模型測試結果比較

結果顯示：（1）從準確度來看，SVM和隨機森林算法的個人信用評價明顯好于樸素貝葉斯和決策樹，其對正常用戶分類的準確率分別為90%和94%，對違約用戶分類的準確率分別為92%和87%。將SVM與隨機森林對比發現，SVM能更好地捕捉違約用戶，隨機森林可以更好地捕捉正常用戶。（2）從召回率來看，SVM對正常用戶的召回率最高達到97%，隨機森林對違約用戶的召回率最高達到84%，說明上述機器學習的算法，能夠有效地將目標用戶查全，避免遺漏。結合F1值來看，SVM和隨機森林算法在綜合評價方面同樣表現較好。

4 結 論

本文通過搜集和整理P2P平臺1 000名真實客戶信息，運用4種不同的機器學習算法對客戶的信用進行分類評價，并對各算法結果進行比較。結果表明：機器學習個人征信模型相比傳統個人征信評價在數據來源相同的情況下，可以避免主觀上的失誤，結果更加明確和直觀。從實際效果來看，SVM和隨機森林是當前較為成熟的個人征信模型算法，準確度和召回率較高，可適用于商業銀行、P2P、小貸公司等機構進行個人征信評價。機器學習算法在樣本數量較少、個人數據相對不足的情況下也能夠對個人征信有著較為準確的評價。在大數據背景下，未來個人征信數據將會更加充足，基于機器學習算法的個人征信模型可以進一步優化數據處理和算法，提高個人征信評模型的準確度。