二維粗糙面兩束波束散射特性研究

思黛蓉,王明軍,陳新欣

(西安理工大學自動化與信息工程學院,陜西 西安 710048)

1 引 言

近年來,隨機粗糙面電磁散射特性研究取得重要的突破,被廣泛地應用在國防軍事領域和工程領域[1-3]。許多研究者利用Kirchhoff理論處理隨機粗糙表面散射特性,基爾霍夫理論是一種電磁理論,被稱為“切平面理論”,這一理論被應用于計算粗糙表面相干部分和漫射部分的光散射特性[3-5]。

在粗糙面中,大多數研究者都是對粗糙表面一束波束散射特性進行研究。郭立新等人利用基爾霍夫近似,研究粗糙面電磁散射,得到了平均散射強度系數及方差的表達式,并討論散射場與分維及粗糙面其他參量之間的定量關系[1]。國外學者Jafari G R等人[2]引入了一種非微擾雙尺度Kirchhoff理論,它既考慮大尺度粗糙度,又考慮小尺度粗糙度。通過利用原子力顯微鏡圖像計算光散射強度,證實理論與實驗結果吻合較好。M Nieto-Vesperinas等人[5]首次提出隨機粗糙表面兩束高斯光束的多次散射,對兩束相干光束表面的散射進行了計算機模擬。M V Glazov等人[6]采用基爾霍夫理論,研究隨機粗糙金屬表面的光散射強度問題,得到金屬表面有規則的結構來改變相干與非相干散射比值的關系。李恪等人[7]通過對激光海面漫反射特性研究,數值計算、分析二維激光光束的散射系數與遮蔽效應。M Salami等人[8-9]推導了粗糙表面兩束波束的相干散射和漫散射強度的解析表達式,討論相干強度干擾項對粗糙表面總散射強度的影響。Yura H T等人[10]推導了兩束入射光束的解析表達式,分析空間濾波對動態散斑圖的影響,得到照明光束的散射特性。Zhang Geng等人[11-12]利用高斯矩定理,推導出不同孔徑粗糙平面散斑場強度起伏的空間互相關函數及粗糙體目標后向散射散斑橫向尺寸的表達式,得出目標形狀不同,對應的散斑形狀也不同。郭冠軍等人[13]利用激光散斑特性得到散射場相關函數和強度二階矩的表達式,并計算激光散斑的面積。M Salami等人[14]根據粗糙表面的統計特性,通過考慮粗糙表面陰影效應,得出有陰影效應的相干散射強度大于沒有陰影效應的散射強度,漫射強度的變化與此相反,且探測角度的變化與散射強度成反比。楊彬等人[15]利用海面兩種多波束后向散射強度歸一化方法,驗證和對比兩種方法的有效性。賀鋒濤等人[16]研究激光光束在水下傳輸,建立了光斑擴展模型,分析光強被海水中的物質吸收和散射,光束強度逐漸減弱。目前,眾多學者對粗糙表面單波束散射強度的研究頗多[1-4,6,7,11],然而,近年來對粗糙表面多波束散射特性的研究甚少。

本文以Kirchhoff理論為基礎,研究粗糙表面兩束波束的相干散射強度和漫射強度,推導粗糙表面兩束波束散射強度歸一化相關系數的表達式。數值分析兩束波束強度相關系數及單波束、兩束波束表面相干散射強度比值的影響因素,為后期討論更有實際意義的三維粗糙目標散斑探測等問題的研究奠定基礎。

2 隨機粗糙表面散射

圖1 粗糙表面散射示意圖

遠區散射場表達式:

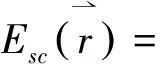
(1)

其中,h(x,y)是點(x,y)處表面高度函數,且:

(2)

由式(1)可知,平均散射場為:

(3)

其中,AM=4XY為平均散射表面的面積,總散射強度分為兩個部分:一個是相干散射強度,另一個是漫射強度,在鏡面反射方向上看到的大部分是相干散射強度。粗糙表面相干散射強度表示為:

(4)

其中,g=k2C2σ2,Io是光滑表面的相干散射強度;σ為表面均方根高度,影響光束的兩個重要因素是光束的光斑大小和入射光束的波長。

平均漫射場強度表達式為:

(5)

高斯粗糙表面一維、二維特征函數表示為:

(6)

其中,令g=k2C2σ2,ρ(R)為高斯粗糙表面的相關函數。將式(6)代入式(5)可得:

[egρ(R)-1]RdR

(7)

3 隨機粗糙表面兩束波束的散射特性

3.1 隨機粗糙表面兩束波束的相干散射場

粗糙表面兩束波束的散射示意圖如圖2所示。假設兩束波束波長相同,則:

k1=k2=k

入射波矢分別為:

散射波矢為:

圖2 粗糙表面兩束波束的散射示意圖

兩束波束的散射場分別為:

(8)

平均散射場可表示為:

〈Esc〉=〈Esc1+Esc2〉

=χ(kC1)〈Esc01〉+e-iφ0χ(kC2)〈Esc02〉

(9)

相干強度可表示為:

=e-g1I01+e-g2I02+2e-(g1+g2)/2

(10)

3.2 隨機粗糙表面漫射場及散射相關系數

粗糙面兩波束的平均漫射場強度表達式為:

〈Id〉=〈(Esc1+Esc2)(Esc1+Esc2)*〉

-〈(Esc1+Esc2)〉〈(Esc1+Esc2)*〉

=〈Id1〉+〈Id2〉+〈Id21〉+〈Id12〉

(11)

其中,由式(11)可知,第一項和第二項分別是第一束、第二束波束的平均漫射場強度,第三項和第四項表示漫射場的干擾強度。由式(7)得:

(12)

其中:

由變量替換得:

漫射場的干擾強度可簡化為:

[χ2(kC2,-kC1,R)-χ(kC2)χ*(kC1)]

(13)

同理,可得:

(14)

將式(12)、式(13)、式(14)代入式(11),得:

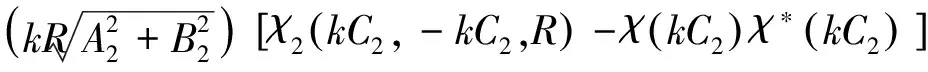
χ(kC2)χ*(kC1)]}

(15)

由式(10)和式(15)可知,總散射強度可定義為:

〈It〉=〈Ic〉+〈Id〉

(16)

C12=〈I1I2〉-〈I1〉〈I2〉

(17)

(18)

4 數值計算及分析

圖3 粗糙表面波束Ic/Io隨入射角變化

圖4 不同入射角下漫射強度的變化

圖5和圖6給出相關長度和不同的入射角度對漫射場強度有影響,相關長度的變化與漫射場強度成正比。對于不同的入射角和方位角,由圖6可以看出總散射強度受干擾項散射強度的影響較大,且總散射強度的后向散射效應增強,可由式(15)可證。

由圖5可知,光波束波長的變化對散射強度影響較大,隨著波束波長的減小,漫散射強度逐漸變小。從圖5(a)～圖5(c)可以看出隨著角度差Δθi變大,不同波長處的漫射強度均減小,且后向散射效應增強,即波束干擾越嚴重。通過對比圖5(a)與圖5(d),可以發現粗糙度σ變大,漫射強度增大且波束干擾減弱。

圖5 不同相關長度下漫射強度隨散射角變化

圖6 漫射強度隨不同角度的變化

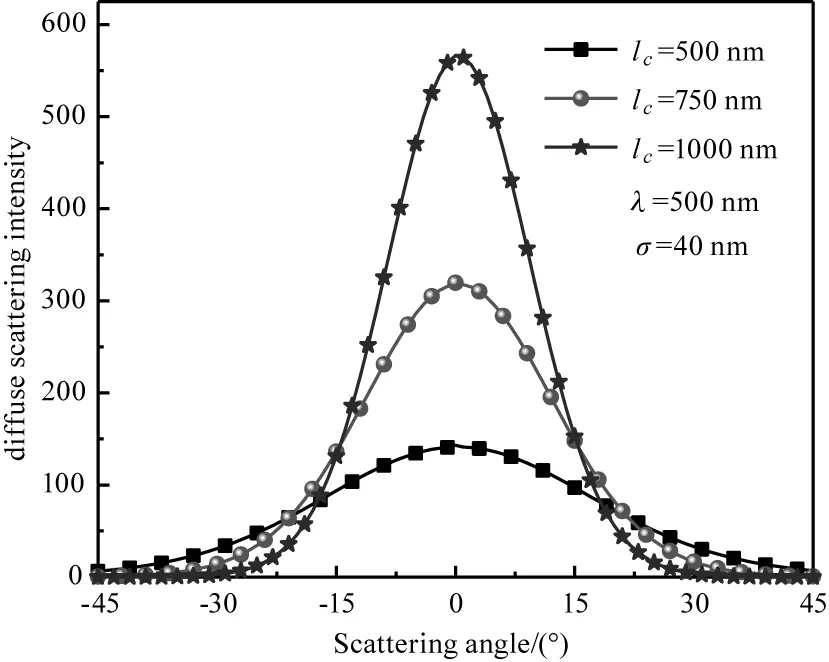
圖7 波長不同時漫射場強度隨散射角的變化

由圖8和圖9可看出散射角、kσ的增大對散射強度相關系數有影響,在圖8和圖9(b)中,隨著角度差Δθi增大,散射強度相關系數變小；由圖9(a)可知,增大相關長度,鏡反射方向的峰值也增加,散射強度主要集中在鏡反射方向。

圖8 不同入射角下γ12隨kσ的變化

圖9 不同條件下γ12隨散射角的變化

5 結 論

根據Kirchhoff理論,研究二維高斯粗糙表面散射強度,討論兩束波束的總散射強度、相關系數受干擾強度、角度差等因素的影響。通過數值方法分析兩束波束漫射強度和散射強度相關系數隨角度差、粗糙度及相關函數的變化情況,結果表明:

(1)散射角對粗糙表面的相干散射強度與光滑表面的相干散射強度比值有影響。當兩束波束入射角、方位角均相等時,說明兩波束相互重合且散射強度比值是單波束比值的四倍；如果兩束波束入射角、方位角中有一個角度不相等,根據式(10)可知,由于干擾強度的影響,相干散射強度減小。

(2)粗糙度、相關長度等影響因素的變化與漫射強度均成正比,隨著角度差Δθi增大,漫散場強度的后向散射效應逐漸增強,意味著兩束波束的干擾越嚴重。

(3)總散射強度受干擾項散射強度的影響較大,且總散射強度的后向散射效應增強。

(4)相關長度的變化與散射強度相關系數成正比,隨著角度差Δθi增大,散射強度相關系數變小,則鏡反射方向的峰值減小且并未產生后向散射效應。

綜上所述,通過對粗糙表面兩束波束的散射特性研究,討論漫射強度及散射強度相關系數受哪些因素影響。發現干擾項不僅出現在總散射場中,而且還出現在漫射場中,數值計算多波束散射強度相關系數為研究復雜粗糙目標的散斑統計特性等問題提供理論依據。