高旋二維彈道修正彈的角運動特性
朱 煌,史金光,謝 飛,徐東輝
(1.南京理工大學(xué) 能源與動力工程學(xué)院,江蘇 南京210094;2.遼沈工業(yè)集團有限公司 研發(fā)中心設(shè)計二所,遼寧 沈陽110045)
彈道修正彈成本低、命中精度高、附帶毀傷小,在現(xiàn)代戰(zhàn)爭中具有至關(guān)重要的地位。精確制導(dǎo)組件(precision guidance kit,PGK)是美國陸軍最早提出的高旋二維彈道修正彈引信項目,通過在常規(guī)炮彈上加裝低成本GPS制導(dǎo)引信組件實現(xiàn)炮彈精度的提高[1]。近年來,美國ATK公司研究的PGK為典型代表,通過控制固定鴨舵相對于彈體的滾轉(zhuǎn)角度,使操縱舵在大地坐標(biāo)系中的位置固定,由此產(chǎn)生相應(yīng)的修正力與力矩來實現(xiàn)彈道精確控制[2]。美國軍方提出的XM1156“精確制導(dǎo)組件(PGK)”二維彈道修正引信,預(yù)期的圓概率誤差達到50 m[3]。文獻[4-5]建立了該類彈丸角運動方程,研究了其飛行穩(wěn)定性及其在脈沖力作用下的運動特性。文獻[6-7]研究了彈丸在重力和控制力作用下的動態(tài)響應(yīng)特性、強迫運動特性等問題。張嘉易等[8]研究了鴨舵修正機構(gòu)的氣動特性,對幾種不同形狀、不同面積鴨舵的阻力、升力及各項力矩進行了分析,并研究了不同形狀舵片在相同時間點進行彈道修正后的修正能力。袁備等[9]對不同舵偏角和受力面積下的鴨舵所受阻力、升力和導(dǎo)轉(zhuǎn)力矩以及相關(guān)系數(shù)進行動力學(xué)仿真。許諾等[10]基于周期平均的概念提出一種能連續(xù)地控制平均法向力的大小和方向的修正方法。吳映鋒等[11]研究了無控、有控時彈丸的攻角與速度運動特性。
本文在上述研究成果的基礎(chǔ)上,建立了高旋二維彈道修正彈的角運動方程,推導(dǎo)了彈丸在起始擾動作用下的攻角與速度偏角的變化關(guān)系,研究了彈丸在脈沖控制力和固定方位控制力長時間作用的2種情況下的彈軸運動特性,進行了數(shù)值計算分析,驗證了在控制力作用下的攻角、速度偏角規(guī)律,為控制策略與控制方案的設(shè)計提供了理論依據(jù)。
1 PGK組件概述
PGK組件由互相垂直的2對舵面組成,1對旋轉(zhuǎn)舵片按照相同舵偏角差動安裝,來流在2個舵面產(chǎn)生大小相等、方向相反的氣動力,其合力為0,如圖2所示。產(chǎn)生的合力矩使彈軸旋轉(zhuǎn),同時在舵面上生成相應(yīng)的滾轉(zhuǎn)阻尼力矩反對彈丸滾轉(zhuǎn),滾轉(zhuǎn)阻尼力矩隨著轉(zhuǎn)速增大而增大,當(dāng)2個力矩的和為0時,轉(zhuǎn)速達到平衡。
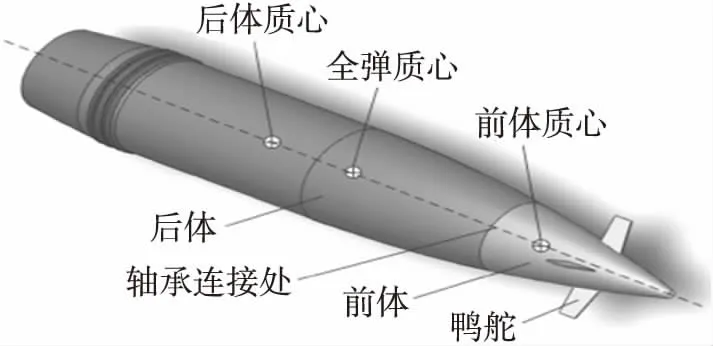
圖1 鴨式布局雙旋彈結(jié)構(gòu)示意圖
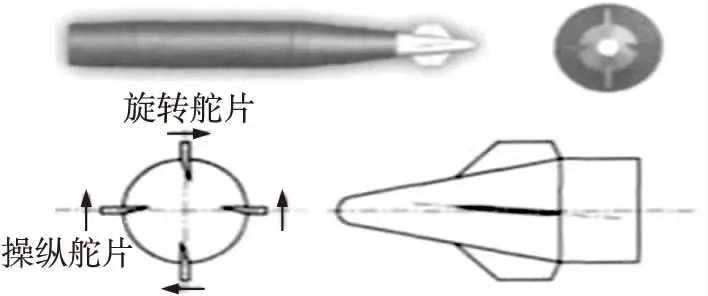
圖2 PGK組件舵面安裝情況
1對操縱舵片按同向偏轉(zhuǎn)固定角安裝,2片舵面上產(chǎn)生的升力方向相同,升力對彈丸質(zhì)心形成的力矩影響彈丸角運動,產(chǎn)生攻角,影響全彈的氣動力,進而改變彈丸的運動軌跡。
2 高旋二維彈道修正彈的角運動模型
對于高旋二維彈道修正彈,由于PGK組件的質(zhì)量、體積相對于全彈來說較小,故可以忽略其質(zhì)量和體積,不改變?nèi)珡椀馁|(zhì)量分布特性與軸對稱性,主要考慮組件增加的控制力和力矩。通過在無控彈角運動基礎(chǔ)上增加控制組件提供的控制力和力矩來建立其角運動方程。
建立的攻角角運動方程為[12]
Δ″+(H-iωp)Δ′-(kz+iωpMT)Δ=G
(1)
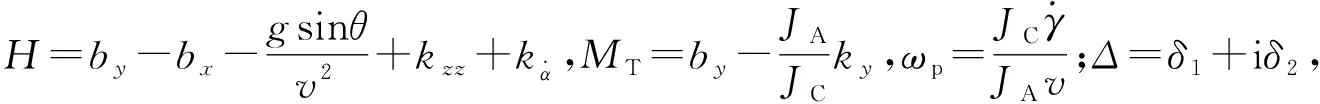
速度偏角方程為[12]
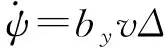
(2)
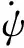
方程(1)右端的G為非齊次項,包含重力的影響、風(fēng)的影響、輕微不對稱因素的強迫作用、控制力和力矩的作用等。
在一段彈道上,認(rèn)為空氣動力變化較小,近似看作常數(shù),攻角方程(1)和偏角方程(2)就可作為常系數(shù)微分方程,對其進行求解。
3 高旋二維彈道修正彈的角運動特性
3.1 起始擾動作用下彈丸的角運動特性
Δ″-iωpΔ′-kzΔ=0
(3)
其特征方程的特征根為
(4)
式中:
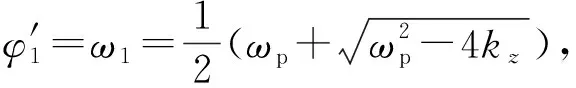
其中:φ′j=ωj,j=1,2,是對飛行弧長而言的角頻率。
考慮靜力矩為翻轉(zhuǎn)力矩,彈丸滿足陀螺穩(wěn)定性時,方程(3)的解為
Δ=C1eiφ′1s+C2eiφ′2s
(5)
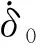
(6)
或
(7)
式中:
ω1t=ω1v0,ω2t=ω2v0
(8)
(9)
式(7)表示彈軸繞速度線的攻角運動是由2個圓運動合成,2個圓的幅值相等,角頻率均為正,即2個圓運動方向相同,其合成運動的曲線為外擺線,如圖3所示。
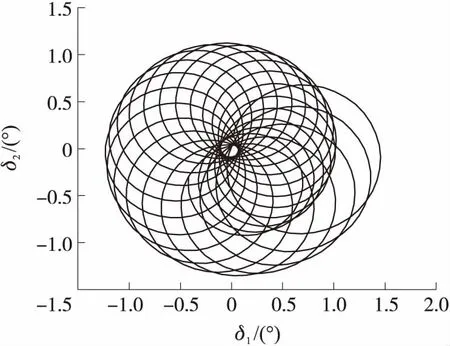
圖3 起始擾動時的攻角曲線
3.2 起始擾動作用下的平均速度方向
方程(2)描述了速度方向圍繞理想質(zhì)點彈道速度方向的變化規(guī)律。當(dāng)存在攻角Δ=δ1+iδ2時,由攻角產(chǎn)生的升力方向與復(fù)攻角矢量方向平行,大小為mbyv2|Δ|,速度方向根據(jù)升力的方向偏轉(zhuǎn),即滿足偏角方程(2),則
ψ′=ψ′1+iψ′2=byΔ
(10)
由于ψ′的方向是沿偏角ψ變化的切向,所以從幾何上講,ψ′平行于攻角曲線的割線。
(11)
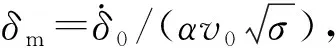
(12)
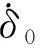
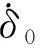
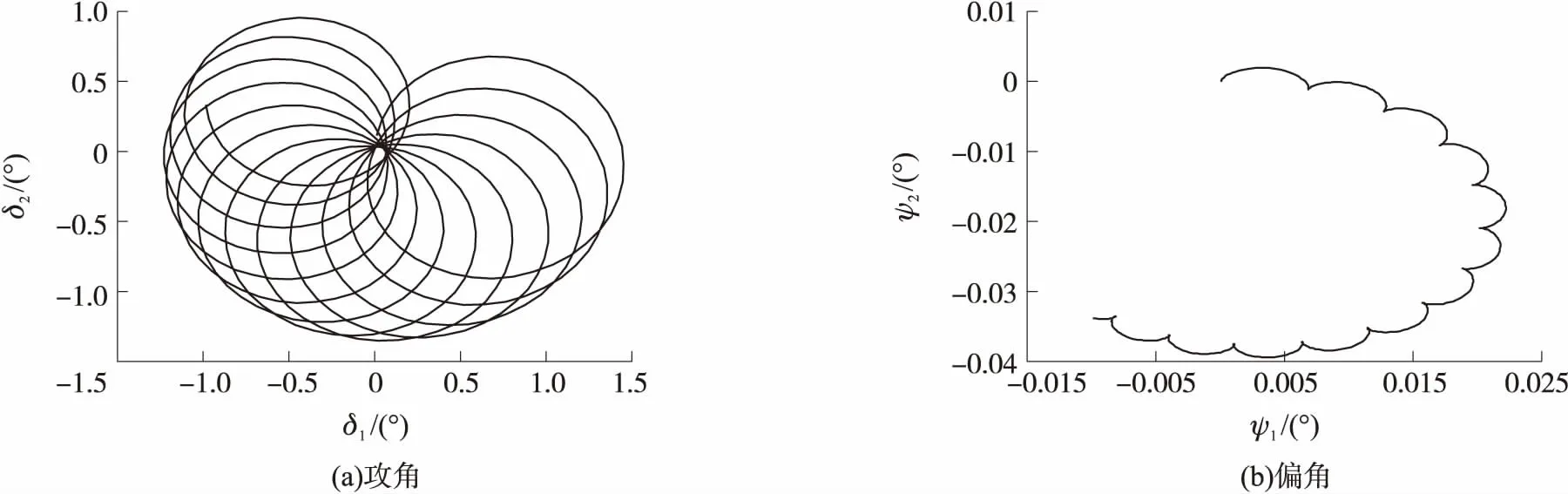
圖向上時0.5 s內(nèi)的攻角曲線、偏角曲線

圖向下時0.5 s內(nèi)的攻角曲線、偏角曲線
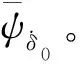

圖向右時0.5 s內(nèi)的攻角曲線、偏角曲線

圖向左時0.5 s內(nèi)的攻角曲線、偏角曲線
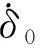
3.3 控制力瞬時作用下的彈軸運動特性
彈丸受到瞬時控制力是指升力舵面短暫地鎖定停留在某一方位一段很短的時間Δt,形成此方向的升力和控制力矩,此后解鎖,舵面相對彈體自由旋轉(zhuǎn)而不提供確定方位的升力。此時可看作在普通力作用基礎(chǔ)上增加了瞬時控制力矩時的作用效果。
以下假定攻角較小,氣流始終與舵面垂直,升力與舵面垂直,大小不變。分析舵面產(chǎn)生向上和向下方向的控制力時,對彈丸質(zhì)心產(chǎn)生控制力矩作用下的攻角和偏角變化規(guī)律。
圖8、圖9分別為產(chǎn)生向上、向下的控制力時的彈軸運動規(guī)律。
對比圖8與圖4、圖9與圖5可見,二者的運動規(guī)律相似,瞬時控制力所產(chǎn)生的平衡攻角、平均速度偏角的方向與瞬時控制力方向大致相反。

圖8 控制力向上,0.5 s內(nèi)的攻角曲線、偏角曲線

圖9 控制力向下,0.5 s內(nèi)的攻角曲線、偏角曲線
3.4 控制力較長時間作用下的彈軸運動特性
固定方位控制力指在小攻角條件下,舵面長時間停留在某個方位而形成固定方向控制力和控制力矩,從而研究彈丸角運動的長期平均響應(yīng)。
此時彈丸受到平行于彈軸的氣流,由升力面固定舵偏角δD產(chǎn)生升力FD0,FD0就是控制力,方向沿舵面法線方向。
以彈軸坐標(biāo)系Oξηζ[12]的近似鉛直面Oξη為彈體滾轉(zhuǎn)角的零位置,設(shè)舵面法線方向相對于此零位置的滾轉(zhuǎn)角為φD,則升力FD0也在φD方向,它沿彈體坐標(biāo)系Oη和Oζ的分量為FDη和FDζ。設(shè)Oη為復(fù)數(shù)平面的實軸,Oζ為虛軸,故舵面升力的復(fù)數(shù)形式為
FD=FDη+iFDζ
(13)
設(shè)固定舵面壓力中心到彈丸質(zhì)心的距離為lG,則升力對彈丸質(zhì)心產(chǎn)生的力矩為
MD=MDη+iMDζ=iFDlG
(14)
彈丸繞質(zhì)心轉(zhuǎn)動方程為
(15)
式中:ωη,ωζ分別為沿實軸和虛軸的轉(zhuǎn)速分量;MDη,MDζ為增加的控制力矩。將式(15)第1式乘以(-i),再與第2式相加,得到擺動角Φ的復(fù)數(shù)方程,再與偏角方程相減,得到攻角方程:
Δ″+(H-iωp)Δ′-(kz+iωpMT)Δ=
[|FD|lG/(JAv2)]eiφD
(16)
將方程(16)的解代入偏角方程(2)中積分,可得到飛行速度方向的變化規(guī)律。
假設(shè)在一段彈道上,方程(16)中系數(shù)變化較小,近似看作常數(shù)處理,即方程(16)為線性常系數(shù)方程。
舵面方位角φD隨著控制策略不同而變化,假設(shè)它在一段彈道上為常數(shù),即固定舵停留在某一方位角φD不變,平行于彈軸的氣流產(chǎn)生大小不變的控制力矩|FD|lG,方程右端為常數(shù)項,則方程解為
Δ=δ1+iδ2=C1e(λ1+iω1)s+C2e(λ2+iω2)s+ΔD
(17)

-(kz+iωpMT)Δ=[|FD|lG/(JAv2)]eiφD
其穩(wěn)態(tài)解為
(18)
式中:KD=|FD|lG/(JAv2)。
可見,在固定方位φD舵控力作用下,攻角經(jīng)過一段時間運動后達到平衡值ΔD。
當(dāng)不考慮馬格努斯力矩項時,即MT=0,則式(18)可寫成:
(19)
此時平衡攻角ΔD的方位與舵面法線方向φD相反,相差180°。
當(dāng)考慮馬格努斯力矩項時,即MT≠0,式(18)可寫成:
(20)
式中:Δφ=-arctan(ωpMT/kz),由于馬格努斯力矩項引起的MT較小,Δφ為一小角度。
由式(20)可以看出,平衡攻角ΔD的方位在角度(φD+Δφ)的相反方向上,即在舵面法線方向φD相反的180°附近,相差一個小角度Δφ。
為了驗證上述規(guī)律,以某大口徑二維彈道修正彈為例,利用六自由度剛體彈道方程,設(shè)置操縱舵舵偏角FD0=6°,舵面壓力中心到彈丸質(zhì)心的距離lG=500 mm,控制時間為3 s,分析3 s內(nèi)的彈軸運動規(guī)律。圖10、圖11分別給出了控制力向上、向下作用3 s內(nèi)的攻角、速度偏角曲線。
由圖10和圖11可知,在固定方位φD舵控力長時間作用下,平衡攻角、平均速度偏角的方向與控制力方向近似成180°,相差一個小的角度Δφ。
圖12、圖13分別給出了全彈道上控制力向上、向下作用時的攻角、速度偏角曲線。

圖10 控制力向上,3 s內(nèi)的攻角曲線、偏角曲線

圖11 控制力向下,3 s內(nèi)的攻角曲線、偏角曲線

圖12 全彈道控制力向上時的攻角、偏角曲線

圖13 全彈道控制力向下時的攻角、偏角曲線
由圖12和圖13可知,在全彈道上固定方位舵控力作用下,彈丸的攻角運動規(guī)律是由舵控力產(chǎn)生相反方向的攻角與重力產(chǎn)生向右的動力平衡角合成的,平均速度偏角方向為該合成攻角的方向,該速度方向?qū)⒂绊憦椀赖馁|(zhì)心運動,實現(xiàn)彈道修正。
4 結(jié)論
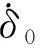
②彈丸在瞬時控制力作用下,產(chǎn)生的平衡攻角、平均速度偏角的方向與瞬時控制力方向大致相反;
③彈丸在固定方位舵控力長時間作用下,平衡攻角、平均速度偏角的方向與控制力方向近似成180°,相差一個小的角度Δφ;
④彈丸在全彈道上作用固定方位舵控力,彈丸的攻角運動是由舵控力產(chǎn)生相反方向的攻角與重力產(chǎn)生向右的動力平衡角合成的,平均速度偏角方向為該合成攻角的方向。

