基于Beam-based近場動力學模型的材料沖擊響應研究

劉 寧,王 帥,胡夢凡

(南京理工大學 機械工程學院,江蘇 南京 210094)

用傳統數值方法研究陶瓷裝甲、混凝土工事等抗彈材料侵徹毀傷問題時,還不能提供完整的沖擊破壞圖像對沖擊破壞過程給予動力學一致的分析,限制了結構防護的性能優化和評價。材料沖擊破壞是一個裂紋形成、擴展、分叉直到最終破碎的復雜過程,經典連續介質力學理論在處理這種高度非線性和不連續性問題時具有一定的局限性,主要難點在于經典連續理論的數學模型是基于連續性假設下的包含空間導數的偏微分方程,一旦所研究的問題出現損傷、裂紋擴展、分層、斷裂和穿透等不連續問題時則不存在位移偏導數,從而出現求解困難。

近年來一種新興的基于非局部思想的近場動力學方法(Peridynamics,PD)從根本上解決了傳統數值方法面臨的求解困難,該方法已在模擬裂紋萌生、擴展、分離等不連續問題時表現出了獨特的優勢[1-2]。PD理論與經典連續介質力學最大的區別在于,PD方法使用空間積分方程來描述物質力學行為,而經典連續介質力學是基于位移的導數建立運動方程。PD理論的這一特征表明,材料域內任意位置的損傷的萌發和擴展是自發產生的,并且可沿任意路徑進行,而不需要特別引入任何裂紋擴展準則[3]。

近場動力學理論體系中鍵基模型(bond-based PD)得到了廣泛應用[4-5],但常規鍵基模型只考慮了物質點間的軸向力作用,僅有一個“材料常數”,導致了對材料泊松比的限制,如平面應力問題材料泊松比為1/3,三維問題泊松比限制為1/4,制約了鍵基近場動力學模型的應用范圍。本文基于有限元Euler-Bernoulli梁單元模型思想[6-9],提出一種新型Beam-based近場動力學本構關系,突破常規鍵基近場動力學模型對材料泊松比的限制,通過算例驗證新型PD模型對沖擊動力學問題的適用性。

1 Beam-based PD模型

1.1 Bond-based PD基本理論

PD理論將物質體系看作由眾多物質點構成,每個物質點具有確定的體積和密度,空間域Ω內的物質點x與其周圍δ范圍內的物質點x′∈Ω:‖x′-x‖≤δ存在相互作用力f,如圖1所示,在任意時刻t,物質點x的運動方程為

(1)

式中:ρ為物質密度,u為物質點x的位移,e為體力密度,H代表了物質點x的近場鄰域范圍。

定義參考構形中物質點x與x′之間相對位置矢量ξ和相對位移矢量η分別為

ξ=x′-x,η=u′-u

(2)

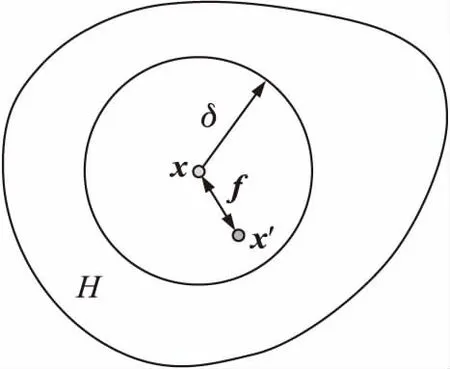
圖1 PD理論模型

對于Bond-based PD模型,式(1)中物質點間的相互作用力f可以寫為

(3)

式中:c為材料微彈性模量,可看作近場動力學理論中的“材料常數”;s為物質點之間鍵相對伸長率:

(4)

通過PD理論中應變能密度與經典彈性力學中應變能密度的等價關系[5],可推導出PD微彈性模量c,如平面應力問題微彈性模量:

(5)

式中:E為彈性模量;ν為泊松比,且為1/3,三維問題的泊松比限制為1/4,固定的泊松比限制了Bond-based PD模型的應用范圍和求解精度。

在近場動力學中,某物質點的破壞程度用近場域內與該粒子有相互作用的鍵的斷裂比例表征:

(6)

式中:μ為物質點之間鍵是否斷裂的判據,即

(7)

式中:s0為鍵的臨界伸長率。μ=1,表示物質點之間鍵未發生斷裂;μ=0,表示鍵已斷裂。

1.2 Beam-based PD模型的構建

基于有限元Euler-Bernoulli梁單元模型,在Bond-based PD模型的基礎上加入了物質點間相對轉動效應,建立了新型Beam-based PD模型,物質點間作用力由軸向力密度f1與切向力密度f2兩部分構成,如圖2所示,(x,x′)為初始構形,(y,y′)為現時構形。

Beam-based PD本構方程可以表示為

f=CS

(8)

式中:C為微彈性模量矩陣,可通過應變能密度等效方法推導;S為物質點相對伸長率矢量。在小變形情況下,參考有限元Euler-Bernoulli梁單元模型,將物質點相對伸長率矢量S進行泰勒展開和線性化處理:

(9)

式中:u1,u2,u′1,u′2分別為物質點變形前后軸向和切向位移矢量,r為物質點間相對位置矢量。

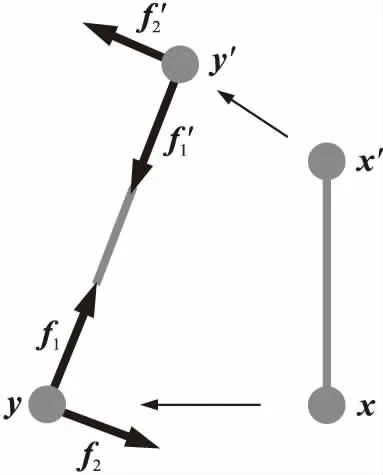
圖2 梁模型物質點運動

1.2.1 二維Beam-based PD模型

二維情況下Beam-based PD本構函數可寫為

(10)

式中:c1,c2分別為軸向和切向微彈性模量。

由式(9)可得物質點間軸向力與切向力表達式:

(11)

在二維笛卡爾坐標系下,物質點間軸向相對位移與切向相對位移可通過物質點坐標相對位移分量表示,如圖3所示。

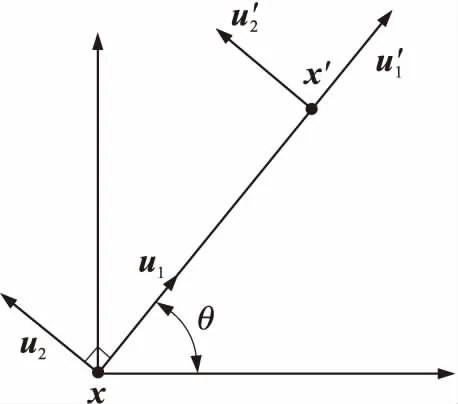
圖3 二維梁模型物質點位移分量示意圖

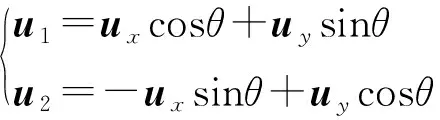
(12)

將式(12)帶入式(11)可得:

(13)

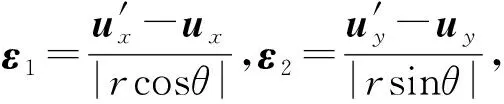
物質點間“梁單元”具有的微勢能為

(14)

物質點x的應變能密度為

(15)

同時,在彈性力學中,平面應力問題的應變能密度為

(16)

根據應變能密度等效法,由式(15)、式(16)可得Beam-based PD模型軸向微彈性模量c1與切向微彈性模量c2:

(17)

寫成矩陣形式:

(18)

式(17)中c1與c2為2個相互獨立的PD常數,其中c1>0,c2≥0。可見對于平面應力問題,Beam-based PD模型的泊松比取值范圍為(-1,1/3],大大擴展了傳統鍵基PD模型的應用范圍。

同理,可推導平面應變問題中Beam-based PD模型微彈性模量矩陣:

(19)

式中的泊松比范圍為(-1,1/4]。

1.2.2 三維Beam-based PD模型

三維情況下Beam-based PD本構方程可寫為

(20)

寫成分量形式:

(21)

三維條件下物質點間“梁單元”微勢能為

(22)

積分可得三維PD應變能密度:

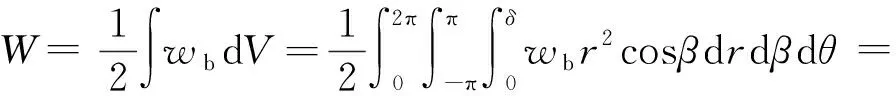
(23)

而經典彈性力學中三維應變能密度為

(24)

通過應變能密度等效方法,可得三維Beam-based PD模型微彈性模量:

(25)

寫成矩陣形式:

(26)

式中:c1>0,c2≥0,三維Beam-based PD模型泊松比范圍為(-1,1/4]。

2 數值方法

2.1 離散方程

將計算域進行離散,運動方程式(1)的離散形式可表示為

(27)

式中:i表示當前物質點,n為時間迭代步數,Vj為當前物質點i的鄰域內物質點j的體積。

2.2 PD沖擊接觸算法

將沖擊彈丸視為剛體,在沖擊過程中彈丸不斷把被沖擊材料物質點從其運動軌跡上排擠開,如圖4所示,受排擠物質點速度為

(28)

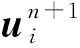
(29)

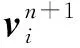
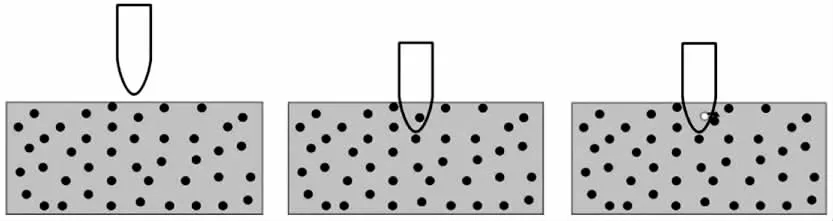
圖4 剛性體沖擊接觸模型

3 算例研究

3.1 平板沖擊

圖5為剛性圓盤沖擊矩形板模型[10],圓盤質量m=1.57 kg,直徑D=50 mm,以速度v0=32 m/s沖擊無約束矩形板上邊緣中間位置,矩形板長l=200 mm,寬b=100 mm,厚度d=9 mm,密度ρ=8 000 kg/m3,彈性模量E=191 GPa,泊松比ν=1/3。采用Beam-based PD模型計算圓盤沖擊過程,離散物質點間距Δx=1 mm,近場鄰域范圍δ=3.015dx,時間步長Δt=0.1 μs。

圖6為不同時刻矩形板內部應力波云圖,由圖可見,在圓盤沖擊矩形板后,應力波以沖擊點為圓心,以半圓形輻射狀向周圍傳播,應力波傳播到左、右邊界和底部邊界時發生反射,多次反射后形成了復雜的應力分布特征,但在整個沖擊過程中矩形板僅發生彈性形變,沒有發生破壞。

圖5 圓盤沖擊矩形板模型

圖6 矩形平板應力波傳播云圖

為了驗證Beam-based PD模型對不同泊松比材料的適用性,進一步計算了泊松比ν=1/4時矩形板中心的沖擊響應,作為對比同時給出了有限元計算結果,如圖7所示。

圖7 泊松比為0.25時中心點位移變化曲線

由圖7可見,本文模型計算結果與有限元結果吻合較好,驗證了本文模型的正確性,新型PD模型有效拓展了Bond-based模型的應用范圍。

3.2 三維Kalthoff-Winkler沖擊模型

Kalthoff-Winkler沖擊試驗是用剛性圓柱彈丸沖擊帶有對稱預置裂紋的馬氏體時效鋼靶板,觀測裂紋的擴展過程,包括裂紋擴展方向和擴展速度等[11]。試驗結果表明,圓柱體撞擊靶板時產生沖擊壓縮波,使得裂紋從裂尖處開始擴展,產生Ⅱ型裂紋,最終形成的裂紋與預制裂紋夾角約為70°。Kalthoff-Winkler沖擊試驗已成為研究材料動態斷裂本構模型和數值方法的經典驗證算例。Kalthoff-Winkler沖擊模型如圖8所示,材料參數如表1所示。圖中,圓柱直徑D=50 mm,沖擊速度v0=32 m/s,靶板長度l=200 mm,厚度d=9 mm,寬度b=100 mm,預制裂紋長l0=50 mm,間距h=50 mm,裂紋寬度a=1.5 mm。

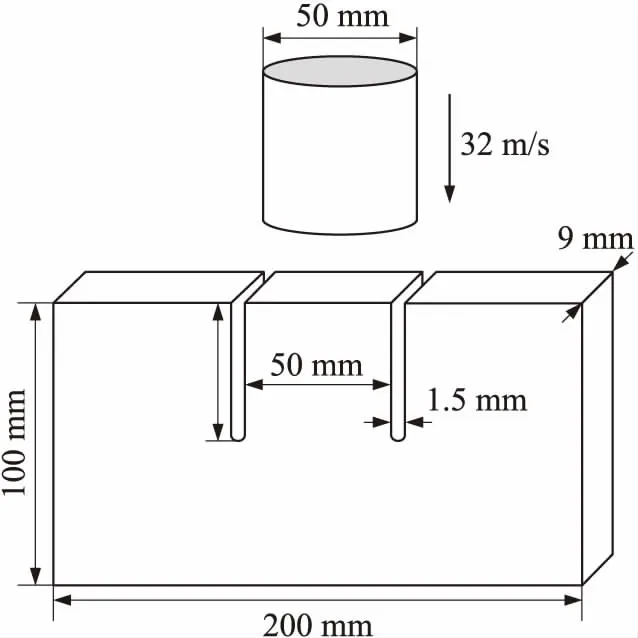
圖8 Kalthoff-Winkler試驗幾何模型

表1 靶板材料參數

E/GPaρ/(kg·m-3)ν1907 8300.3

采用Beam-based PD模型模擬Kalthoff-Winkler沖擊試驗,取物質點間距Δx=1 mm,近場鄰域δ=3.015dx,材料臨界伸長率s0=0.01,時間步長Δt=0.58 μs。

圖9為Beam-based PD模擬的裂紋擴展過程,裂紋從預制裂紋尖端開始擴展,幾乎沿一條直線對稱擴展至靶板左、右兩側邊緣,裂紋擴展方向與預制裂紋夾角大約為68.3°。圖10為文獻[12]給出的Kalthoff-Winkler沖擊試驗結果和擴展有限元仿真結果。由圖可見,本文模擬的裂紋擴展過程與試驗值吻合較好。

眾所周知,傳統有限元法難以直接模擬材料破壞過程,而改進的擴展有限元法需要人為設置合適的破壞準則才能模擬裂紋擴展。本文建立的Beam-based PD模型不僅擴展了傳統鍵基模型的適用范圍,還能夠模擬裂紋的自然萌生和自發擴展過程,無需任何外部干預,在處理材料沖擊破壞問題時顯示出巨大的優勢,為沖擊動力學研究提供了新的研究手段。

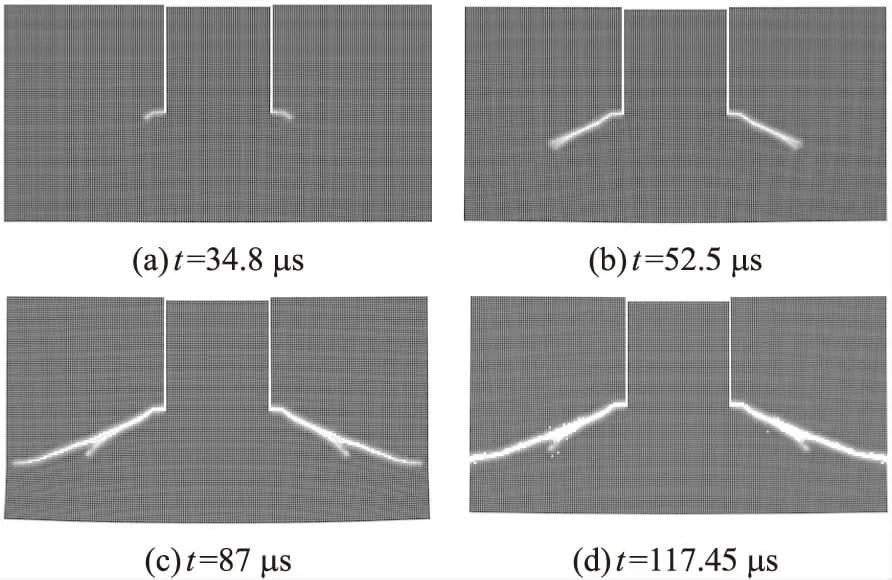
圖9 Beam-based PD模擬的裂紋擴展過程

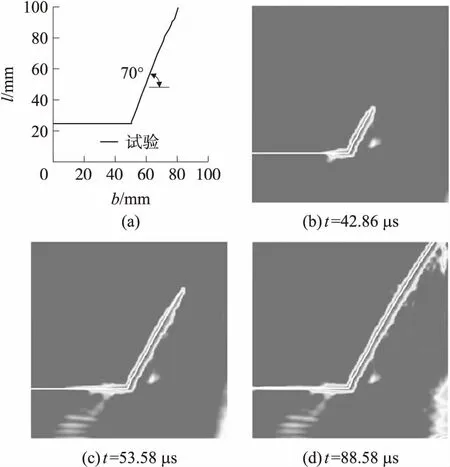
圖10 Kalthoff-Winkler試驗及擴展有限元結果[12]

4 結束語

本文針對常規Bond-based近場動力學模型對材料泊松比的限制,借鑒有限元Euler-Bernoulli梁單元模型,在Bond-based模型的基礎上加入了物質點間相對轉動效應,建立了新型Beam-based PD本構模型,有效拓展了泊松比范圍。圓盤沖擊矩形板模擬結果表明,泊松比對動態沖擊響應具有重要影響,本文模型能夠正確反映材料泊松比效應。模擬了Kalthoff-Winkler靶板沖擊過程,裂紋擴展角度和裂紋擴展速度與試驗結果吻合較好,新型Beam-based PD模型能以材料真實泊松比準確計算沖擊載荷作用下材料的變形和破壞過程。本文模型對認識脆性材料沖擊破壞的復雜物理機制具有明顯優勢,為沖擊動力學問題研究提供了一條新的技術途徑。