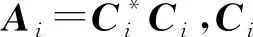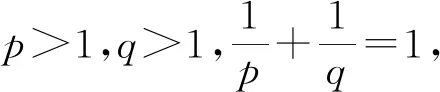關于Hardmard乘積下和幻方跡的若干不等式

劉娟娟，劉興祥，張 婧

(延安大學數學與計算機科學學院，陜西延安716000)

幻陣學是矩陣理論中非常重要的內容，其廣泛應用于密碼學、文件管理、人口流動等方面。而幻陣學對于研究矩陣不等式的相關問題也有很大價值和影響，其中幻陣學的分支——和幻方的定義及其跡的不等式前人還沒有研究過。本文在給出和幻方相關定義的基礎上，主要研究了關于Hardmard乘積下和幻方跡的幾個簡單的不等式，對于豐富矩陣不等式的研究內容，完善矩陣不等式的框架體系具有重要意義。

1 和幻方的相關定義

定義1 設F是數域，如果矩陣A=(aij)n×n∈Fn×n滿足

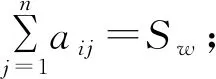
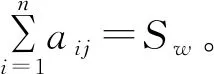
則稱矩陣A稱為數域F上的n階弱和幻方，并稱Sw為數域F上n階弱和幻方A的弱幻和。

定義2 設F是數域，如果矩陣A=(aij)n×n∈Fn×n滿足

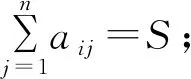
則稱矩陣A稱為數域F上的n階和幻方，并稱S為數域F上n階和幻方A的幻和。

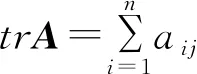
2 矩陣不等式

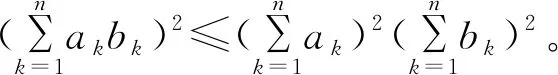
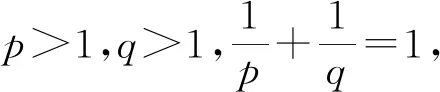
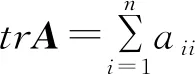
角元，則有tr(A°B)≤trA·trB。

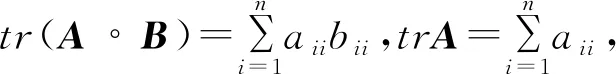
由Cacuchy不等式可知tr(A°B)≤trA·trB成立。

引理4[5,6]設A為n×n階Hermite半正定矩陣，則trAn≤(trA)n。

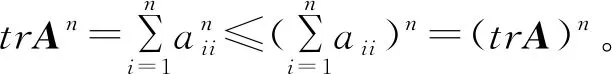
3 和幻方的不等式

定理1 設矩陣A，B分別為數域F上的n階和幻方，幻和分別為SA，SB，其中A=C*C,B=D*D,C,D為數域F上的n階Hermite半正定矩陣，則tr(A°B)2≤(SA·SB)2。

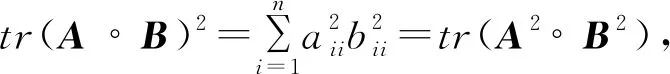
(SA)2(SB)2=(SA·SB)2，

所以tr(A°B)2≤(SA·SB)2成立。

推論1 設矩陣A，B分別為數域F上的n階和幻方，幻和分別為SA，SB，其中A=C*C，B=D*D，C，D為數域F上的n階Hermite半正定矩陣，則tr(A°B)n≤(SA·SB)n。

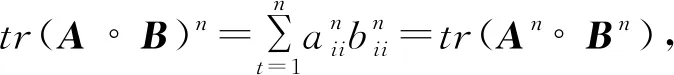
(SA)n(SB)n=(SA·SB)n，

所以tr(A°B)n≤(SA·SB)n成立。

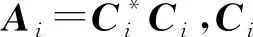
證明：采用第一數學歸納法來證明：

n=1,trA1=SA1，

n=2,tr(A1°A2)=trA1·trA2=SA1·SA2，

假設n=k時命題成立，即

當n=k+1時