淹沒條件下水射流噴嘴內外流場特性*

曾施雨，王 濤，劉辛愉，邵偉峰

(長江重慶航運工程勘察設計院，重慶 401147)

長江橫貫我國東、中、西三大經濟地帶，是連通西南、華中和華東地區的水路交通運輸大動脈，同時也是我國的重要生態寶庫。隨著長江經濟帶及國家內河水運發展戰略的實施，對提升長江黃金水道的功能和增強航運能力提出了新的要求。長江上游內河航道整治工程中，常采用水下爆破的方式清除礁石。爆破工藝雖然技術成熟、工效較高，但其所產生的附加影響會造成水生生物的致命損傷和水體環境的污染破壞。因此，研發一種環保的新型清礁技術，對于推動未來長江經濟帶的“生態優先、綠色發展”是極其必要的。

水射流技術起源于20世紀50年代，可實現對材料進行清洗、切割和破碎，最初主要應用于礦床中的采煤工程。如今，已廣泛應用于機械、航空、石油、水利等行業。1983年起，美國礦業局已經在水射流破巖領域進行了廣泛研究[1]。1995年，王瑞和等[2]對水射流破巖鉆孔及旋轉射流破巖成孔進行試驗研究，初步探究了射流破巖過程及原理。盧義玉等[3]對射流輔助刀具的切割裝置進行研發，并進行了破巖試驗。孫清德等[4]開展水力聯合機械鉆孔破巖的試驗研究，結果表明其效率高于單射流或單鉆齒的作業方式。

水射流技術具有切割能力強、取材方便、環保無污染、工作機件易于實現自動控制等優點。本文提出在水下淹沒環境下應用水射流切割礁石以代替傳統的爆破工藝，現階段主要研究淹沒水深及水流流速等外界環境因素對沖擊射流的影響。

1 水射流數學模型

1.1 模型建立

整個模型計算域主要由噴嘴及其外空間水域兩部分構成。噴嘴為常見的錐直型結構，考慮其本身具有極好的對稱性，故可將計算簡化為二維數學模型問題進行求解。水下淹沒空間為一個寬20 cm、高25 cm的水箱結構，噴嘴位于其頂部中央。計算網格采用結構化網格，其中噴嘴結構的網格尺寸進行加密處理。二維模型和錐直型噴嘴結構如圖1所示，其中入口直徑D為6 mm，入口段長度L1為20 mm，收斂段長度L2為17.55 mm，圓柱段長度L3為6 mm，收斂角α為13°，出口直徑d為2 mm。

圖1 二維模型和錐直型噴嘴結構

1.2 計算參數設置

假定整個水射流運動為不可壓縮流動，體系溫度始終保持不變，與外界無熱交換。噴嘴進口連接高壓管道，出口處于水下淹沒環境，故分別設置為壓力入口和壓力出口；噴嘴壁面為墻體邊界。

水箱頂部與外界大氣環境相通，水箱兩側處于淹沒環境中，均設置為壓力出口；水箱底部為墻體邊界條件。選擇k-ε湍流模型進行模擬計算，離散方程組采用SIMPLE算法[5]進行求解。

1.3 模型驗證

1.3.1淹沒射流結構特性

淹沒射流如圖2所示，射流主要分為初始段、基本段兩部分[6-7]。其中初始段為噴嘴出口至轉折面之間的區域，為射流的核心區，此階段射流集束性好，沖擊速度大，沿程速度幾乎保持不變。轉折面之后為射流的基本段，射流紊動特性增強，速度沿程衰減加劇，逐步呈現出散射現象。

圖2 淹沒射流

根據機械能守恒原理，忽略噴嘴出入口兩點間的高度差，由伯努利方程可推導出式(1)，同時射流流動滿足連續性方程：

(1)

ρv1A1=ρv2A2

(2)

式中：p1為噴嘴入口截面壓強(MPa)；p2為噴嘴出口截面壓強(MPa)；v1為噴嘴入口截面平均流速(ms)；v2為噴嘴出口截面平均流速(ms)；A1為噴嘴入口截面面積(m2)；A2為噴嘴出口截面面積(m2)；ρ為水體密度(kgm3)。

本試驗中6片試驗梁以剪力連接度為分組依據，分為完全連接結合梁(FCB梁組)和部分連接結合梁(PCB梁組)，分別進行動力響應的測試。每組試驗梁又根據不同的栓釘損傷工況各分為3片梁(FCB、FCB1、FCB2和PCB、PCB1、PCB2)，以進行栓釘局部損傷識別的研究，試驗梁其它參數均相同。本文只進行動力響應部分的試驗研究。

因整個噴嘴內部結構均為圓管形，故由式(1)、(2)可推導出：

(3)

式中：D為噴嘴入口直徑(m)；d為噴嘴出口直徑(m)。淹沒環境下(水深2 m)的圍壓不足0.05 MPa，遠小于數十兆帕的射流泵壓，故計算中可忽略p2的影響。針對噴嘴結構尺寸而言，(dD)4數值太小(約等于0)。故可簡化得到噴嘴出口射流沖擊速度的理論計算公式[8-9]：

(4)

1.3.2計算結果

圖3 入口壓力為50 MPa的水射流速度等值線

圖4 入口壓力為90 MPa的水射流速度等值線

由圖3、4可知，噴嘴出口處附近射流沖擊速度達到最大，沿程分布形態呈倒三角形，射流未發生明顯擴散，且始終維持高速狀態。隨后，射流后半段沖擊速度大幅度衰減，沿程擴散加劇。整個流場分布符合經典理論中淹沒射流流場分布特征。

噴嘴中軸線位置的速度變化如圖5所示。水射流噴嘴內外速度沿程發展變化可分為4個階段[10]:1)入口段：射流基本維持其初始狀態，速度變化較小；2)收斂段：噴嘴內部過流斷面面積逐漸減小，水射流壓能得以更大程度地轉化為動能，沖擊速度得到極大提高，且臨近收斂段末端期提升速率更快；3)圓柱段：噴嘴截面尺寸保持不變，水流在該區域平順過渡，沖擊速度略有提高；4)噴嘴外流場：臨近噴嘴出口存在一明顯初始段，長度約1.4 cm，射流始終處于高速狀態。隨后進入基本段，速度沿程發生大幅度衰減。

圖5 噴嘴中軸線位置速度變化

距噴嘴出口3d處水平截面速度分布如圖6所示(d為噴嘴出口直徑)。距噴嘴出口3d水平截面處，仍處于射流初始段內，越靠近軸線處射流速度越大。伴隨著射流的擴散，遠離射流軸線的兩側與四周環境水體接觸摻混，射流能量迅速消散，沖擊速度明顯減小。

圖6 距噴嘴出口3d處水平截面速度分布

1.3.3驗證結果

考慮到噴嘴出口直徑極小，出口截面軸心速度可近似代替截面平均流速，由表1可知，不同泵壓條件下，其數模計算結果均略小于理論公式計算值。同樣，數模成果表明，射流初始段無量綱長度約為7，與國內外學者的現有研究結果一致(表2)。

表1 水射流噴嘴出口速度

表2 水射流無量綱初始段長度成果

注：l為初始段長度。

通過射流噴嘴出口截面處速度大小和初始段長度兩方面的綜合分析可知，本文的研究成果與其他學者成果具有較好的相似性，所建模型滿足計算精度的要求。

2 淹沒環境對射流的影響

2.1 淹沒水深對射流的影響

伴隨著三峽大壩的調節過程，長江上游庫區水深高差最大約30 m。在泵壓50 MPa的情況下，對比分析水深為2、4、8、18、30 m不同工況條件下的射流流場變化。不同水深下中軸線位置速度差值分布如圖7所示。

注：以水深h=2 m為參照；軸向起點為噴嘴出口。圖7 不同水深下中軸線位置速度差值分布

由圖7可知，對比淹沒水深2 m情況下，水深增加到4和8 m時，射流沿程速度整體變化較小；當水深增加到18和30 m時，射流初始段以及基本段速度沿程速度均出現相對明顯地衰減，基本段后部分速度最大衰減可達17 ms左右。

注：以水深h=2 m為參照；截面位于距噴嘴出口3d處。圖8 不同水深下水平截面速度差值分布

分析可知，出現上述現象的原因在于數十米水深的環境圍壓對比射流的高泵壓而言，其大小并非處于同一數量級。高壓條件下的水射流具有極高的沖擊速度，其中初始段為射流能量最為集中的區域，沖擊速度大、集束性好，不易受到外界環境的影響。

2.2 水流流速對射流的影響

2.2.1射流流場分布變化

不同水流流速下的射流流場分布如圖9所示。

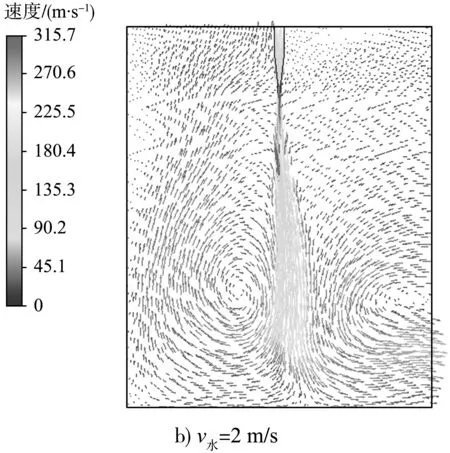
圖9 不同水流流速下的射流流場分布

射流初始段和基本段水平截面上沿x軸方向速度u的分布特征如圖10所示。當水流流速v水=0 ms時，射流兩個階段內沿水平方向上的速度分量都很小，整體波動范圍僅在-4～4 ms。伴隨著淹沒環境中水流沖擊速度的增加，射流速度分量u逐漸明顯增大，其中初始段內速度u增量在1～8.5 ms，基本段速度u增量在4～20 ms。整體來看，淹沒環境中水流流動會對射流沿程發展造成一定的影響，其中相比射流基本段而言，射流初始段仍能保持較好的穩定性。

圖10 射流水平截面處速度u分布

2.2.2射流壓強分布變化

動壓是表述對流體單位體積動能大小的物理量，其基本概念源于伯努利方程：

E=12ρv2

(5)

式中：ρ為水體密度(kgm3)；v為流體流速(ms)。流體動壓大小主要與其密度、運動速度相關。在射流沖擊破壞巖石的過程中，沖擊荷載是關鍵因素。射流的沖擊速度越大，其動壓越大，破巖效果越好。

淹沒條件下水射流動壓分布與速度分布特征相似，射流動壓最高且分布最為集中的區域位于射流基本段，如圖11、12所示。長江上游河段礁石分布以頁巖與泥巖為主，其極限抗壓強度多在20～40 MPa。對比可知，在泵壓50 MPa條件下，水射流最大沖擊動壓可達49.8 MPa，大于靶物對象巖石的抗壓強度，可實現對其切割破壞。

注：淹沒水深2 m，環境流速0 ms。圖11 泵壓50 MPa的水射流動壓等值線

注：淹沒水深2 m，環境流速0 ms，軸向起點為噴嘴出口。圖12 泵壓50 MPa的中軸線位置水射流速度-動壓分布

3 結論

1)射流噴嘴內外的沿程發展主要分為4個階段，其中噴嘴收斂段加速作用最為明顯。臨近噴嘴出口處的外流場區域中，射流存在明顯的初始段，其無量綱長度約等于7。

2)淹沒水深30 m的范圍內，伴隨水深深度的增加，射流沿程沖擊速度有所減小。整體來看，射流初始段受水深條件影響極小，軸心速度減小不足5 ms，衰減程度僅約1.5%。水深在18～30 m時，射流衰減的程度相對更為明顯，其中基本段區域軸心速度最大衰減可達約17 ms。

4)淹沒條件下水射流動壓分布與速度分布特征相似，初始段為射流動壓最高且最為集中分布的區域。