基于FLUENT的垂向二維數值波浪水槽的造波效果*

童朝鋒，魏芷陽，孟艷秋

(河海大學 港口海岸與近海工程學院，江蘇 南京 210098)

基于FLUENT流體力學模型建立數值波浪水槽是波浪與建筑物之間相互作用研究的經典方法，周勤俊等[1]基于RANS方程和兩方程湍流模型，采用有限體積法，首次提出了適用于VOF方法的源造波、消波技術;其后孫大鵬等[2]、趙艷等[3]采用計算流體力學模型成功利用源項、推板、速度邊界造波法建立基于FLUENT的數值波浪水槽，FLUENT流體力學模型開始廣泛應用。近年來國內外新的數值造波方法層出不窮，Jacobsen等[4]將基于BOUSSINESQ水波方程的造波方法成功應用到了開源代碼OpenFOAM中取得了較好的造波效果;Wang等[5]基于CIP模型成功模擬了孤立波與水下建筑物的相互作用；Losada 等[6]、Higuera等[7]分別建立了基于COBRAS-UC模型、OpenFOAM模型的數值波浪水槽模型模擬了波浪與建筑物之間相互作用過程，取得了較好的效果。

相比之下，FLUENT作為最常用的計算流體力學模型，操作簡便、界面友好，具有先進的數值仿真和強大的前、后處理功能，在計算流體力學領域和實際工程中具有極強的應用價值。基于FLUENT的數值造波方法根據造波原理主要有源項造波法、推板造波法和速度邊界造波法3種。為達到波浪的精準數值仿真，須充分了解各種造波法造波效果以及達到最佳造波效果應采用的網格尺寸，但目前尚無相關文獻對此進行詳細對比分析。

為此，本文應用FLUENT流體力學計算模型，采用上述3種造波法，分別建立不同網格尺寸和波陡條件下的數值波浪水槽，結合線性波和二階、三階Stokes波理論，對比不同方法的仿真結果及與理論波浪形態之差異，分析3種造波法的優缺點，討論采用不同波浪方程、不同網格尺寸對仿真結果的影響，為利用數值波浪水槽開展波浪與建筑物相互作用數值研究提供根據。

1 造波、消波原理及邊界條件設置

1.1 數值波浪仿真模型

波浪數值仿真采用FLUENT流體力學軟件，其軟件選取顯式或隱式差分格式，非耦合隱式算法、耦合顯式算法或耦合隱式算法等數值計算方法求解Navier-Stokes方程，可精確模擬層流、湍流、多相流等各類流體力學問題，軟件提供用戶自定義函數便于二次開發。本文數值波浪水槽模擬采用二階迎風格式、PISO算法、k-ε模型，結合VOF模型和幾何重構法進行液面捕捉，獲得較為精準的模擬結果。

1.2 造波原理及邊界條件

1.2.1源項造波法

源項造波法原理是通過UDF二次編譯功能在造波源區域給動量方程添加動量源項s(x,y,t)，使造波源區域中水質點具有運動速度，并在重力作用下水面升降形成波浪。根據相關文獻[8-9]，造波源區域高度宜取水深的23，或使造波源區域上方水體高度約為1倍波高，寬度宜取波長的150。實際計算時可選取大致合適的尺寸，再不斷試算調整選取最佳造波源尺寸。

數值水浪水槽如圖1所示。造波源區域設在入口處，波浪沿x方向傳播，右端為消波區，消波區長度取1～2倍波長。水槽入口、出口及下部邊界均取固壁邊界，上部為壓力出口。

圖1 數值波浪水槽

造波源函數根據以下公式確定：

(1)

(2)

式中：s(x,y,t)為造波源區域要添加的造波源項；u(x,y,t)為t時刻目標波浪在坐標(x,y)處的水質點水平速度，根據線性波理論或Stokes波理論取值；u、v分別為x、y方向速度；Δx為水平方向網格長度。

1.2.2推板造波法

推板造波法原理與物理模型中推板式造波機相同，其數值波浪水槽與圖1相同，入口處固壁邊界添加動網格以模擬推波板運動。

推板運動速度根據Schaffer等[10-11]推得的推板位移變化與波面高度之間解析關系確定，其水平運動速度函數u(t)如下：

(3)

(4)

式中：η為波面升高，根據Stokes波理論或線性波理論確定其值；ω為角頻率；c0為造波板運動與給定波浪間的傳遞函數；k為波數；d為水深。

1.2.3速度邊界造波法

速度邊界造波法將入口邊界水質點賦予已知相應波水平和垂向周期性振蕩速度，促使水質點運動產生波浪，其數值水槽與圖1相同。數值水槽的造波區入口處邊界設為速度入口邊界，水槽底部和右側為固壁邊界，上部為壓力出口邊界。

數值水槽入口邊界處水質點水平向和垂向速度：

u=u(x,y,t)

(5)

v=v(x,y,t)

(6)

式中：u，v分別為入口邊界水平、豎直方向速度；u(x,y,t)、v(x,y,t)分別為在t時刻坐標(x,y)處水平、豎向速度，其值根據線性波理論或Stokes波理論確定。

1.3 消波方法

采用動量源消波。在消波區，水體動量方程添加阻尼源項：

(7)

(8)

式中：ρ為水密度；p為水壓力；μ為消波系數，為使波浪平緩過渡，μ隨x由0遞增，即:

μ=a(x-x0)

(9)

式中：a為常數，根據經驗其取值范圍為1～50；x0為消波區起始位置水平坐標。

2 模型建立

2.1 網格及模擬工況

波浪要素見表1，波況1～3保持水深和波高不變，只改變周期達到改變波陡的目的。波況1～3采用的水槽總長280 m、高10 m、水深6 m，消波區長30 m。為方便比較，考慮盡可能少的影響條件，波況4采用總長140 m、高8 m、水深6 m的深水數值水槽，探究非線性項對造波效果的影響，水槽消波區長20 m。

表1 數值水槽波況參數

采用a、b、 c、d、e共5種結構化網格，其中網格a水平分辨率Δx=0.4 m，垂向分辨率Δy=0.02 m；網格b的Δx=0.4 m，Δy從液面附近向兩邊遞增，最小為0.02 m，最大為0.1 m；網格c的Δx=0.4 m、Δy=0.05 m；網格d的Δx=0.4 m、Δy=0.12 m；網格e的Δx=0.1 m，Δy從液面附近向兩邊遞增，最小為0.004 m，最大為0.06 m。

為探究垂向網格分辨率對模擬結果的影響，波況1采用a、b、c、d4種網格分別建立數值波浪水槽。網格e用于波況4深水情況下微幅波的模擬計算。波況1～3分別采用3種造波法和線性波、二階Stokes波兩種波浪方程進行模擬，以探究造波法對造波效果的影響。波況4采用3種造波法和線性波、二階、三階Stokes波方程進行模擬，研究數值造波中非線性作用的影響。算例模擬時間步長取0.01 s，每步最多迭代40次，計算總時間超過80 s。

2.2 造波和消波驗證

使用波況1(波陡Hλ=0.043)、網格b、二階波浪方程，則3種造波方法得出的x=λ處水面變化歷時曲線如圖2所示。3種模擬結果都在時間t=10 s左右達到穩定，之后水面隨時間規律性變化，且與理論值吻合良好。模擬得出的x=λ處一個周期內速度和動壓強與理論值對比見圖3。取波峰處時間為T4,波谷處時間為3T4，可以看出模擬值與理論值基本吻合，說明基于FLUENT建立的數值波浪水槽可用于波浪與結構物之間相互作用的研究。

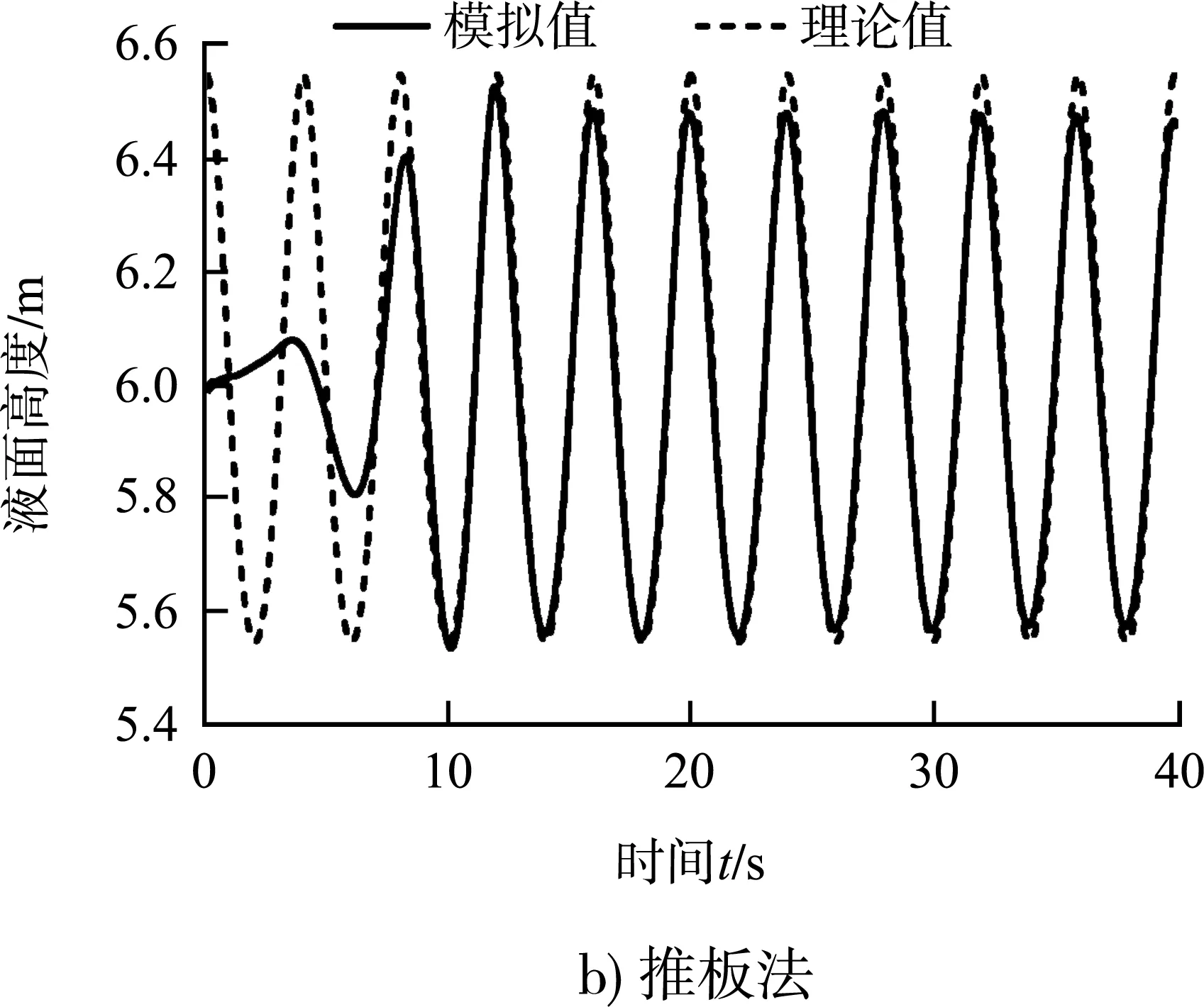
圖2 3種造波法x=λ處液面歷時曲線

波況1使用推板造波法、二階波浪方程,t=60 s時水槽末端水質點速度矢量分布見圖4。結果顯示在非消波區水質點運動速度較大，消波區水質點運動速度逐漸減小，最后變為0，說明消波區消波效果良好。

圖3 推板造波法x=λ處水質點速度、動壓強與理論值對比

圖4 t=60 s時水質點速度矢量分布

3 結果對比與分析

3.1 網格分辨率對數值造波效果影響

采用上述3種造波法、二階波浪方程和4種不同垂向分辨率的網格分別建立數值波浪水槽，模擬仿真波況1的波浪。為便于辨析某一位置處模擬波面與理論波面貼合程度，將自由水面和波高的理論值均取該點處模擬波的平均水面和波高，采用如下均方根相對誤差計算一個周期內模擬值與理論值相對差異，評價模擬仿真效果：

(10)

式中：S為均方根相對誤差；H為波高；ηi為i時刻理論液面高度；η′i為i時刻模擬液面高度；n為一個周期內的數據數量。

不同造波法所造波浪平均水面飄移隨網格分辨率變化如圖5a)所示。源項造波法模擬仿真的水面漂移絕對值受網格尺寸變化影響較大，液面附近垂向網格分辨率Δy取0.02 m時波面漂移絕對值為0 m，隨Δy增加，迅速增加到0.07 m左右；推板造波法模擬結果在Δy≤0.05 m時水面漂移絕對值集中在0.015 m附近，當Δy=0.12 m時偏移量急劇增加至0.06 m；速度邊界造波法模擬仿真結果隨網格步長增加波面漂移量變化不明顯，基本保持在0.02 m左右。

液面高度相對差異隨網格分辨率變化如圖5b)所示。采用源項造波法得出的模擬波形與理論波形之間誤差最大，隨網格變化誤差增加最快；采用推板造波法得出的模擬波形與理論波形吻合最好，相對誤差均較小；使用速度邊界法模擬值在Δy≤0.05 m時誤差較小，Δy=0.12 m時誤差急劇增加。

注：波況1，Hλ=0.043,x=λ處；Δy為0.02、0.02～0.10、0.05、0.12 m分別對應網格a、b、c、d。

圖5采用不同造波方法的水面漂移絕對值和仿真與理論液面高度相對差異隨不同網格分辨率變化

波高沿程變化如圖6所示。可以看出，采用不同分辨率的網格建立數值波浪水槽，隨波浪傳播距離增加，采用不同網格模擬得出的波高值產生差異。其中使用源項造波法造波得出的波高差異最大，使用推板造波法得出的波高差異最小，采用速度邊界造波法得出的沿程波高在網格垂向分辨率Δy≤0.05 m時基本相等，使用Δy=0.12 m的網格時得出的沿程波高與使用其他網格得出的模擬值差異較大。波高隨傳播距離增加持續衰減，衰減到一定程度后逐漸穩定，這是由數值耗散和水體黏性影響產生的正常現象，實際應用中可以增加起始波高，在波高趨于穩定的位置放置建筑物。

圖6 波況1使用不同造波法沿程波高對比

綜上，垂向網格步長越小模擬結果越精確，源項造波法模擬仿真波浪效果對垂向網格分辨率變化比較敏感，液面附近垂向網格分辨率取Δy=0.02 m，即Δy=H50(H為波高)時即可取得較為精確的結果；推板造波法和速度邊界造波法模擬結果對網格分辨率變化敏感性相對較弱，垂向網格分辨率Δy=0.05 m，即Δy=H20時模擬效果較好。

3.2 波陡對數值造波效果影響

根據上述網格對3種造波法造波效果影響分析結果，采用網格b對波況1～3模擬計算，討論波陡對數值造波效果影響。計算分別采用了3種造波法和2種波浪方程。

模擬結果在x=25 m處水面漂移絕對值見圖7。可以看出，波陡相同時采用速度邊界法得出的水面漂移絕對值最大，源項法最小；就波浪方程而言，其他條件相同時，采用不同波浪方程得出的水面漂移絕對值基本相等，說明采用的波浪方程不是影響水面漂移的主要因素。

圖7 不同波陡條件下采用不同波浪方程模擬x=25 m處水面漂移絕對值

模擬結果在x=25 m處一個周期內液面高度與理論值的相對誤差S見圖8。可以看出，其他條件相同時，采用不同波浪方程仿真得出的結果與二階Stokes波理論值吻合均較好。說明造波源不管采用哪種波浪方程，在波浪傳播過程中，模擬結果都會受邊界的非線性作用影響，使波浪呈現出非線性波特性。

圖8 不同波陡和波浪方程模擬液面與理論液面誤差

仿真得出的沿程平均波高對比見圖9。可以看出，采用速度邊界造波法得出的沿程平均波高最大，采用源項法最小；其他條件相同，波陡增大波高衰減速度變快；只改變波浪方程對比模擬結果，使用二階波浪方程得出的沿程平均波高普遍高于使用一階方程得出的結果，波陡越大兩者差異越不明顯。

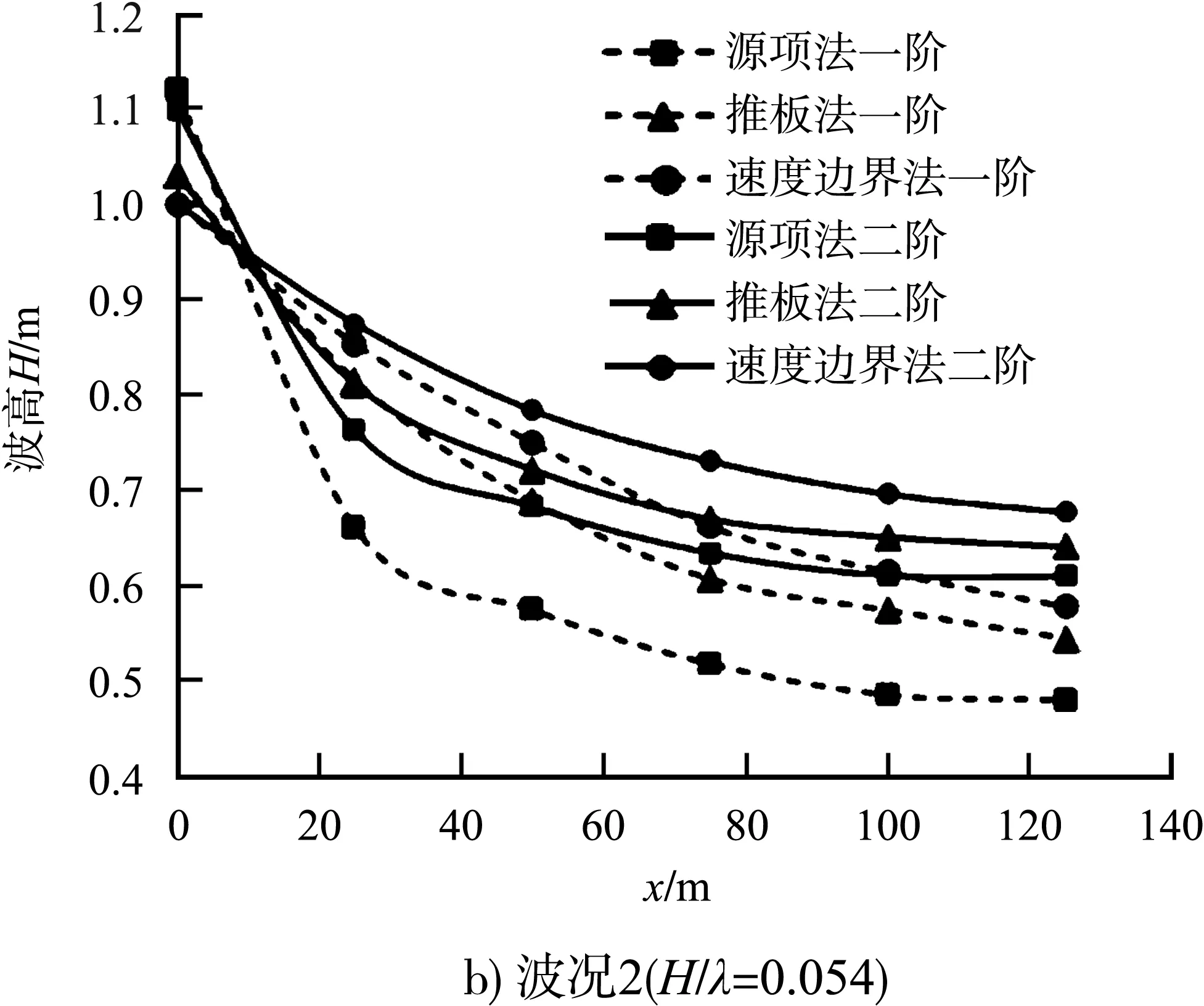
圖9 采用不同造波法和波浪方程模擬沿程平均波高對比

3.3 數值造波中的非線性作用影響

根據上述波陡對數值造波效果影響結果，無論使用哪種波浪方程建立數值波浪水槽，在波浪傳播過程中都會使模擬波面變化接近二階Stokes波理論值。增加波況4(Hλ=0.021)，深水數值水槽算例，研究采用不同波浪方程對造波效果影響。計算分別采用一階、二階、三階波浪方程,其水面漂移絕對值見表2。可以看出，造波方法相同時，使用不同波浪方程得出的水面漂移絕對值完全相等。模擬波面與理論波面相對誤差如圖10所示，造波方法相同時采用的波浪方程階數越高模擬值與同階理論值之間相對誤差越小；低階波傳播過程中受非線性影響，模擬值與相應理論值相對誤差反而大。高階波波形已經體現了非線性項的變形作用，傳播過程中反而變形較小，其模擬值與理論值之間誤差也較小。

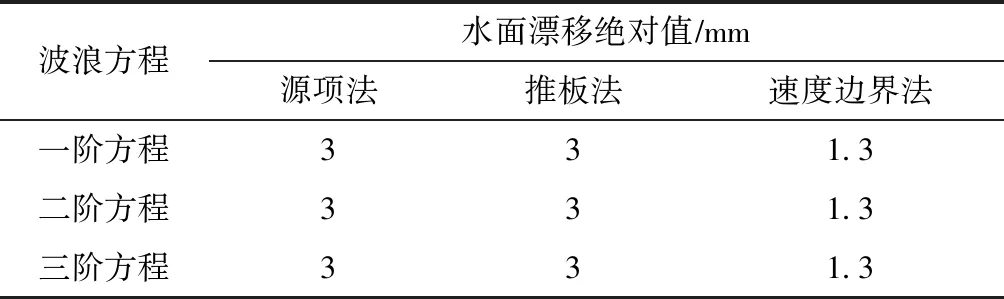
表2 波況4在深水情況下水面漂移絕對值

圖10 波況4在深水條件下模擬波面與理論波面相對誤差

4 結論

1)采用源項造波法造波，波高沿水槽衰減最快；推板造波法采用動網格技術，計算效率相對低，數值造波波形與理論波形最接近；采用速度邊界造波法計算效率最高，數值波高沿水槽衰減速度最小。

2)網格越細模擬結果越精確，采用源項造波法模擬結果對網格尺寸變化最敏感，采用推板造波法和速度邊界造波法模擬結果對網格尺寸變化較不敏感。

3)數值水槽計算中，波陡越大波高衰減越快；數值波浪模擬顯示，在數值水槽的波浪傳播有非線性作用影響，導致即使造波是線性波，傳播到一定距離后，波面也有非線性變形。