談Dandelin雙球模型的構(gòu)建及其教學(xué)價(jià)值①

王海青

(惠州學(xué)院數(shù)學(xué)與大數(shù)據(jù)學(xué)院 516007)

1 問(wèn)題提出的背景

解析幾何以歐幾里得的論證幾何為基礎(chǔ)，通過(guò)坐標(biāo)系以“幾何問(wèn)題→代數(shù)問(wèn)題→求解→反演”的方式將幾何代數(shù)化，把代數(shù)方程與曲線曲面等聯(lián)系起來(lái)，實(shí)現(xiàn)了“數(shù)與形”的靈活轉(zhuǎn)換．解析的方法更具一般性而不過(guò)多地依賴幾何圖形，它改變了歐幾里得幾何的論證方法，使幾何研究變?yōu)榇鷶?shù)計(jì)算，能由已知的代數(shù)結(jié)果發(fā)現(xiàn)新的幾何性質(zhì)．圓錐曲線作為高中解析幾何的核心內(nèi)容在現(xiàn)實(shí)中有非常廣泛而重要的應(yīng)用，一直以來(lái)人們致力于尋求其在天文學(xué)、軍事領(lǐng)域、建筑設(shè)計(jì)等方面有用的性質(zhì)．因此，圓錐曲線相關(guān)內(nèi)容的教學(xué)對(duì)學(xué)生數(shù)學(xué)思維能力和應(yīng)用意識(shí)的培養(yǎng)具有毋庸置疑的重要性．

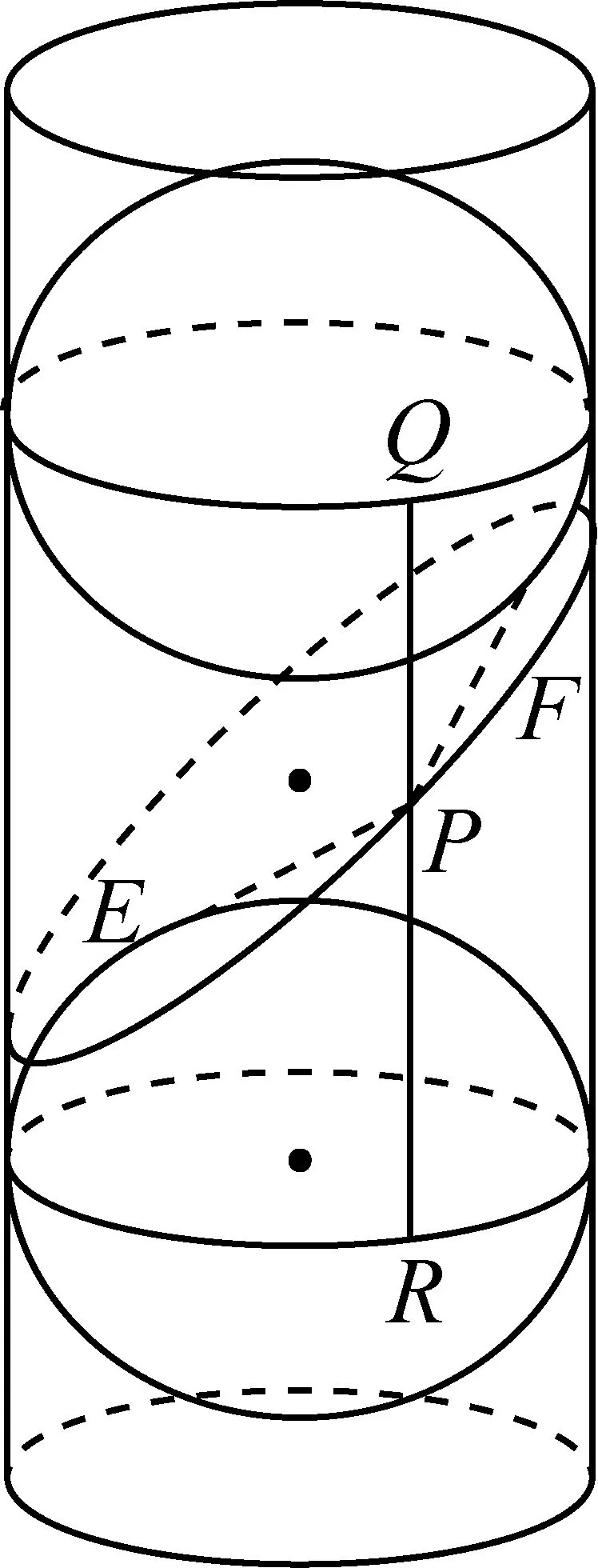
圖2

文[1]以圓錐面Dandelin雙球模型(圖1)和修正后的圓柱面Dandelin雙球模型(圖2)為介質(zhì)，強(qiáng)調(diào)解析幾何教學(xué)回歸“幾何性”的重要性，并指出了“解析性”與“幾何性”并重的教育價(jià)值．[1]解析幾何是連接代數(shù)與幾何的重要橋梁，在教學(xué)中過(guò)于偏重幾何的“解析性”或代數(shù)的“幾何性”都是不可取的，而是要兩者并重強(qiáng)調(diào)“數(shù)與形”的密切結(jié)合．正如文[1]的觀點(diǎn)，在圓錐曲線的教學(xué)中Dandelin雙球模型有助于將代數(shù)化的性質(zhì)直觀化，反映其原有的幾何特征．

但Dandelin雙球模型還承載著更為重要的教學(xué)價(jià)值，即其能揭示圓錐曲線中不同曲線的定義、同一曲線的不同定義之間的密切聯(lián)系，以及三種曲線的特性及其統(tǒng)一性的內(nèi)在關(guān)系．它能實(shí)現(xiàn)從……