第23屆北京高中數學知識應用競賽初賽試題及參考答案

一、下圖所示的是六角星跳棋盤，它是由一些小的正三角形拼出的，如果記棋盤上最小正三角形的邊長為1 cm，六角星的每個角上的三角形的邊長為kcm，就稱這個六角星跳棋盤為“k-六角星棋盤”，下圖就是“3-六角星棋盤”．跳棋盤上的每一個交叉點是旗子可以落下的地方．問：

(1)把“3-六角星棋盤”看成一個網絡地圖，三角形的邊組成這個網絡的道路，這個網絡地圖里的道路總長度是多少？

(2)對于“k-六角星棋盤”構成的網絡地圖，這個網絡地圖里的道路總長度是多少？

(3)能否一筆畫出“3-六角星棋盤”？若能，請給出畫法；若不能，說出至少需要幾筆能畫出來，并給出畫法．

解(1)“3-六角星棋盤”是由三個方向的三組平行線組成，在一個方向上的平行線有11條，其長度和=1+2+9+8+7+6+7+8+9+2+1=60(cm)，因此道路總長度=3×60=180(cm)．

(2)對于“k-六角星棋盤”，過中心點的三條線將棋盤分成六個全等的菱形，如圖3．為了不產生重復計數，菱形的分界線只參加順時針方向菱形的計數，這樣，每個菱形的道路總長是 3k2+k，于是，道路總長度=18k2+6k(cm)．

(3)不能一筆畫出“3-六角星棋盤”．

在一筆畫中，如果一個點既是起點又是終點，那么這個點就應當連出偶數條線段，路過點也如是．觀察右圖中的點A、B、C、D、E、F，與其中每個點相連的三角型的邊都是5條，條數是奇數．也就是說，這6個點中的每個點都得是起點或終點，不能既是起點又是終點，或者是路過點．

而一筆畫圖只有一個起點和一個終點，于是對于下圖來說，至少要三筆畫．

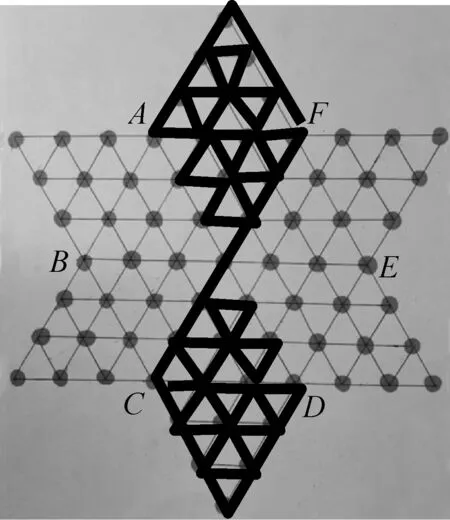
根據對稱性，選擇C為起點，F為終點，構成如上圖……