考慮高差覆冰輸電線路鏈式脫冰振動

晏致濤 李孟珠 熊輝 游溢

摘 ? 要：輸電線路是電網中重要的生命線工程，覆冰荷載是輸電線路最大威脅之一.以國網新疆電力科學研究院某工程為研究對象，采用商業軟件ANSYS進行輸電線路的有限元數值仿真，通過冰單元生死技術實現對覆冰輸電線鏈式和同時脫冰振動的有限元分析，得到等高差和有高差下單跨輸電線脫冰跳躍高度的規律，由此與縮尺模型實驗結果進行對比分析.研究表明：鏈式和同時覆冰導線脫冰模擬結果與實驗吻合很好，相差在5%以內，證明了模擬方式的準確性;在等高差鏈式脫冰下，隨著脫冰速度的增大，最大脫冰跳躍高度會增大逼近到一個定值，而最大軸力不隨脫冰速度變化而變化.有高差鏈式脫冰情況下，保持初張力不變時，隨著高差的增大，跨中最大脫冰跳躍高度近似指數增大，鏈式脫冰的最大跳躍高度逐漸逼近同時脫冰的跳躍高度值;高差的存在會加劇輸電線的上翻情況，也即是脫冰跳躍最大高度大于覆冰后的垂度，可以通過降低輸電線的初張力或者覆冰厚度來減少上翻情況的發生，降低危險隱患.

關鍵詞：架空輸電線路;數值仿真;覆冰;跳躍高度;振動

中圖分類號：TM75 ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標志碼：A

Zippered Deicing Vibration of an Iced Transmission Line

Considering Altitude Difference

YAN Zhitao1，2？覮，LI Mengzhu1，XIONG Hui1，YOU Yi1，3

（1. School of Civil Engineering，Chongqing University，Chongqing 400045，China;

2. School of Architecture and Engineering，Chongqing University of Science & Technology，Chongqing 401331，China;

3. State Grid Xinjiang Electric Power Company Electric Power Research Institute，Urumqi 830011，China）

Abstract：Overhead transmission lines are lifeline projects，and ice load is one of the greatest threat to transmission lines safety. On the basis of the project of Chinese Grid Xinjiang Electric Power Research Institute，the finite element numerical simulation models of overhead transmission lines were established by means of ANSYS software. Using the technique of birth and death of the element for ices，the finite element analyses of zippered and simultaneous ice-shedding vibrations were carried out. By analyzing the modeling parameters of the overhead transmission lines，the influence of altitude difference on the vibration response of single-span ice overhead transmission lines was studied，and compared with the results of the experiment of the scaled model. The results show that the simulations of the zippered and simultaneous ice-shedding are well matched with the experimental results and the discrepancies are less than 5%，which proves the accuracy of the simulation method. If the altitude of two suspension points is the same，the maximum jumping height first increases with the deicing speed and then is maintained at a constant value，while the maximum force is not affected by the deicing speed. If the altitude of the two suspension points is different，the maximum jumping height increases exponentially with the increase of altitude，and the jumping height of the zippered ice-shedding gradually approaches the value of simultaneous ice-shedding when the initial stress is constant. The existence of altitude aggravates the upturn of lines，and the maximum jumping height is greater than the sag of iced line. Meanwhile，the occurrence of upturn can be reduced by decreasing the initial stress and icing thickness of transmission lines.

Key words：overhead transmission lines;numerical simulation;ice shedding;jump height;vibration

覆冰輸電導線的脫冰作為一種突加荷載，很可能會使得輸電導線在脫冰面內引起大幅度的振動，也就是常說的“冰跳”現象.這種現象容易對正常的輸電線路造成閃絡、燒傷、燒斷等危害，同時極易使導線斷股、絕緣子串斷裂情況發生，嚴重時可能會導致輸電塔倒塔，這些危害都會帶來巨大經濟損失[1].輸電線路的覆冰脫冰過程不僅涉及到了多學科的交叉，比如氣象學、結構力學和空氣動力學等 [2]，而且在脫冰過程中輸電導線表現出顯著的幾何非線性特點.

在理論上國內外研究者對輸電線路脫冰問題進行了大量研究. 最初是關于覆冰輸電導線振動方程的研究，通過伽遼金方法，肖錫武等[3]完成脫冰導線的非線性偏微分振動方程，在此基礎上進行了輸電線脫冰振動與幅頻曲線關系的分析研究.之后利用軟件建模分析，候鐳等[4]通過中心差分法，完成了覆冰輸電線路脫冰與脫冰量、檔距組合、均勻與非均勻脫冰方式的關系.在考慮了輸電線脫冰振動的幾何非線性下，晏致濤等[5]得到了脫冰情況下導線跳躍高度、最大水平張力、絕緣子內力和擺動位移、支座反力等的變化規律.Jamaleddine等[6]在商業軟件ADINA的基礎上，通過利用突然卸載的方式模擬覆冰輸電導線的脫冰過程. Laszlo等[7]在ADINA軟件中通過改變導線的密度屬性實現單跨的覆冰輸電線脫冰過程來研究脫冰振動.利用有限元方法，李永平等[8]對單檔的大跨距覆冰輸電導線脫冰跳躍進行了動力響應的分析，得到了輸電線脫冰過程中的跳躍高度和張力的變化規律. 為了簡化模型，魯元兵等[9]用單根導線來模擬分裂導線，完成了對三檔覆冰輸電導線不均勻脫冰過程的數值模擬.同樣采用有限元法，王昕等[10]完成了導線脫冰中脫冰檔數、導線張力和檔距等的參數分析.

除了振動跳躍的規律研究外，國內外的研究者還對脫冰振動控制進行了研究.如劉和云[11]在覆冰模型和相應的數學模型基礎上對導線的覆冰和脫冰跳躍進行了實驗和計算機模擬的研究. 李黎等[12]利用ANSYS/LS-DYNA軟件，采用非線性時程分析法，對覆冰輸電導線的脫冰的振動進行了振動控制的研究，杜運興等[13，14]又對輸電塔線體系及覆冰脫落進行了研究.

自然界中，輸電線的脫冰過程更像是一個鏈式過程，而目前的已有研究幾乎都是以同時脫冰為前提進行仿真分析，對鏈式脫冰的研究比較少，王璋奇等[15，16]對架空線非同時脫冰跳躍進行了實驗研究，同時從動張力的角度研究了脫冰速度對覆冰導線脫冰后導線動張力的變化規律;沈國輝等[17]人也以數值仿真的方法研究了鏈式脫冰中脫冰速度對輸電線路的脫冰影響規律;但他們都沒有考慮到實際地形中的大高差對于輸電線脫冰振動的響應影響.盡管有些學者已經簡單研究了關于高差對脫冰的影響，如陳科全等[18]研究的超高壓輸電線脫冰動力響應數值模擬，研究了高差對導線脫冰后最大冰跳高度的影響規律，但是并沒有考慮鏈式脫冰和大高差對脫冰振動以及懸垂絕緣子運動的影響. 所以目前對輸電線脫冰問題仍需進一步的認識，對覆冰輸電導線的脫冰跳躍響應和脫冰過程中導線的各種參數都有待廣泛及深入的研究.

本文利用3自由度的索單元，建立單跨覆冰輸電導線模型，通過ANSYS的生死單元，來模擬覆冰導線的同時脫冰和鏈式脫冰過程，并與縮尺模型實驗得到的結論進行了對比，證明了鏈式脫冰和同時脫冰的準確性，最后在此基礎上研究了高差對線路脫冰響應的影響.

1 ? 縮尺模型脫冰試驗

進行了單跨導線縮尺模型鏈式脫冰試驗.試驗的幾何相似比為1 ∶ 30，原型檔距為270 m，所以模型的檔距為9 m，為了保證輸電線路的拉伸剛度，使用抗側彎剛度能力低的碳素線作為模擬導線的材料. 為了保證動力相似，實驗采用Froude，Cauchy和Renolds數相似.采用12個集中質量等效覆冰的質量模擬輸電線的覆冰，實驗中通過PCL電路圖依次控制電磁鐵吸盤的磁性來實現集中質量的脫落順序及脫落的時間間隔來完成覆冰脫落的過程，以此來研究不同的脫冰速度下覆冰輸電線路脫冰的過程，利用DIC-3D高速攝像儀來記錄單跨跨中的導線脫冰之后跳躍高度的變化.

該試驗的模型以及原型的參數如表1所示.因為試驗中要用到電磁鐵吸盤，將電磁鐵吸盤均勻分布在輸電線上，而此時的電磁鐵吸盤質量剛好滿足了輸電線的配重質量.覆冰采用懸掛集中小鐵塊方法，其中小鐵塊可以吸附在電磁鐵吸盤上，可以控制電磁鐵磁性來完成脫冰的過程.試驗中的鏈式脫冰是通過試驗中的時間繼電器來實現的，通過在時間繼電器上設置時間間隔來實現電磁鐵吸盤依次失去磁性，而兩個小鐵塊的距離除以時間繼電器的時間間隔就是脫冰速度.

其中PCL電路圖如圖1，右側電路為從中間到兩邊的控制電磁鐵磁性的釋放一次回路圖，即是從中間到兩邊控制釋放電路的執行電路圖;左側電路為從中間到兩邊的控制電磁鐵磁性的釋放二次回路圖，即是從中間到兩邊控制釋放電路的控制電路圖.圖中符號的含義：FU代表熔斷器，SB代表控制按鈕，KM代表接觸器，KT代表時間繼電器，M代表電磁鐵. KM2，KM3，KM4，KM5是具有四對觸點的接觸器，其余的接觸器為具有兩對觸點的接觸器.試驗中只要設定下時間繼電器的時間KT1，然后按下動作按鈕就可以實現鏈式脫冰的過程.

2 ? 輸電線路有限元模擬

2.1 ? 導線建模

由于架空輸電導線是由多股細金屬的鋼芯鋁絞線絞合而成的，其截面尺寸大小遠小于架空導線的檔距，所以可以有以下的假定：1）懸索為只承受拉力，不能承受壓力及彎矩的理想柔性結構;2）材料特性滿足胡克定律.在有限元軟件ANSYS中，Link10單元僅受拉或受壓，且支持大變形效應，將單元剖分足夠細時，適合作為模擬柔性導線的索單元.在進行導線的建模時，實際的輸電線為分裂導線，由于由分裂導線進行建模得到的模擬結果與單根導線差值不大[19]，所以這里采用單根導線來等效分裂導線.將導線分為100個單元.有限元模型相關設置參數見表2.

2.2 ? 絕緣子建模

輸電導線中的絕緣子作用是懸掛導線，當絕緣子兩側輸電導線拉力不平衡時，絕緣子會繞懸掛點發生偏轉，本文采用Link10單元進行建模. 由于脫冰時塔頭順線向位移較小，量級約為0.1 m[14]，遠小于線路檔距;且輸電塔自振基頻要遠大于導線自振基頻[15]. 因此，不考慮輸電塔的剛度對覆冰輸電導線脫冰造成的影響，采用固支來模擬絕緣子在塔架端的自由度約束.

2.3 ? 覆冰脫冰模擬

通常讓覆冰模型簡化為新月形截面包裹在輸電導線的外面 [16]，將覆冰等效為荷載離散地分布在輸電導線的若干點上，分為集中荷載和均勻荷載如圖2所示. Jamaleddine[6]等人已經驗證了利用集中荷載和均勻荷載時覆冰輸電導線的脫冰跳躍響應基本吻合，所以本文采用集中荷載的方法即通過冰單元模擬集中荷載覆冰，同時通過殺死冰單元來實現覆冰輸電導線的脫冰現象. 脫冰方式如圖3所示.在分析建模時直接將覆冰模擬為單元節點處的集中質量，采用Mass21單元模擬集中質量. 在模擬脫冰時，相應的卸載該單元處的等效質量塊，通過控制單元生死來模擬覆冰的同時和鏈式脫落過程.

3 ? 導線找形

導線找形分為導線的自重找形和導線覆冰后找形.導線自重找形采用在懸鏈形基礎上直接迭代法.首先利用懸鏈線方程在兩個懸點之間建立一條直線，之后對該懸鏈線進行網格劃分為一定數量的Link10單元.懸鏈線的兩端點采用全約束，通過材料的實際特性來設置懸鏈線的屬性，實常數以及初應變，再施加重力荷載來逐步更新覆冰輸電導線的有限元模型，以導線的張力作收斂條件進行迭代，最終找形結果就是輸電導線自重荷載情況下的初始變形.

導線覆冰后的找形同樣利用荷載的逐步迭代進行.覆冰采取等效集中荷載方法進行模擬，在導線覆冰找形時以荷載步方式施加荷載，確定覆冰導線最終形狀如圖4所示.

4 ? 鏈式脫冰模擬及參數分析

覆冰輸電線的脫冰模擬工況如表3所示. 下面將分別討論脫冰速度、傾角高差、覆冰厚度以及初張力的影響.

4.1 ? 不同脫冰速度響應分析

通過試驗和模擬研究等高差下脫冰速度分別為7.5 m/s，3.75 m/s和1.875 m/s的鏈式脫冰及同時脫冰，脫冰方向全都設置為從中間到兩邊脫冰，各脫冰工況下導線的初應力89.2 MPa不變，覆冰厚度30 mm，得到不同脫冰速度下跨中跳躍高度數值仿真和試驗的時程對比（圖5）. 圖中顯示吻合效果完好，證明了模擬的準確性，在此基礎上又全面研究了脫冰速度對輸電線路脫冰跳躍響應的影響.

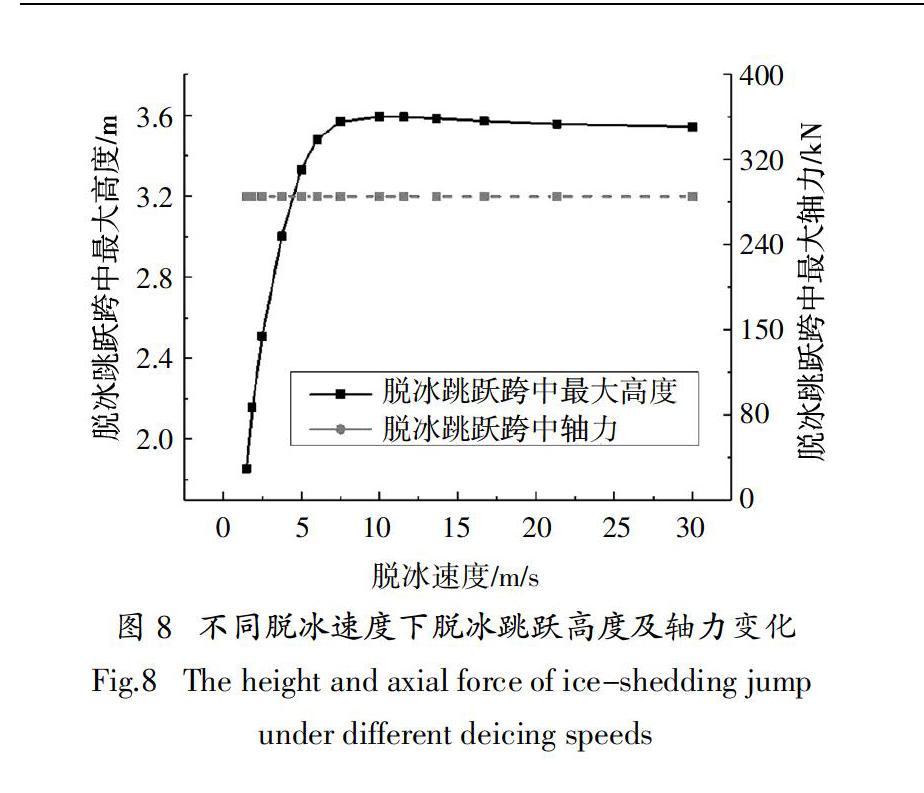
由圖6和圖7可以看出脫冰位移響應和動力響應曲線隨脫冰速度的增大，曲線的頻率逐漸增大.顯然，當脫冰速度增大到一定程度，最大脫冰跳躍高度會逼近收斂到一個定值. 圖8中跨中的脫冰跳躍高度和軸力表明脫冰跳躍最大高度隨著脫冰速度的增大先逐漸增大，然后趨于不變.此時的脫冰跳躍最大高度近似是覆冰后垂度的76.5%.脫冰跳躍的最大軸力始終為初始覆冰后的軸力值，與脫冰速度無關.

4.2 ? 有高差不同傾角的影響

這里考慮兩端掛點不同有高差線路的脫冰振動分析.線路水平檔距仍為270 m，其高差通過兩端掛點與水平夾角來表征.分析模擬了有高差下不同傾角工況來研究高差對于脫冰跳躍響應的影響，設置脫冰方向為從中間到兩邊，保持脫冰速度7.5 m/s、覆冰厚度30 mm和初應力89.2 MPa為不變量進行分析，通過試驗證明模擬準確性后，研究高差對脫冰的影響，得到以下同時脫冰和鏈式脫冰下跨中脫冰跳躍高度隨高差變化的曲線圖.

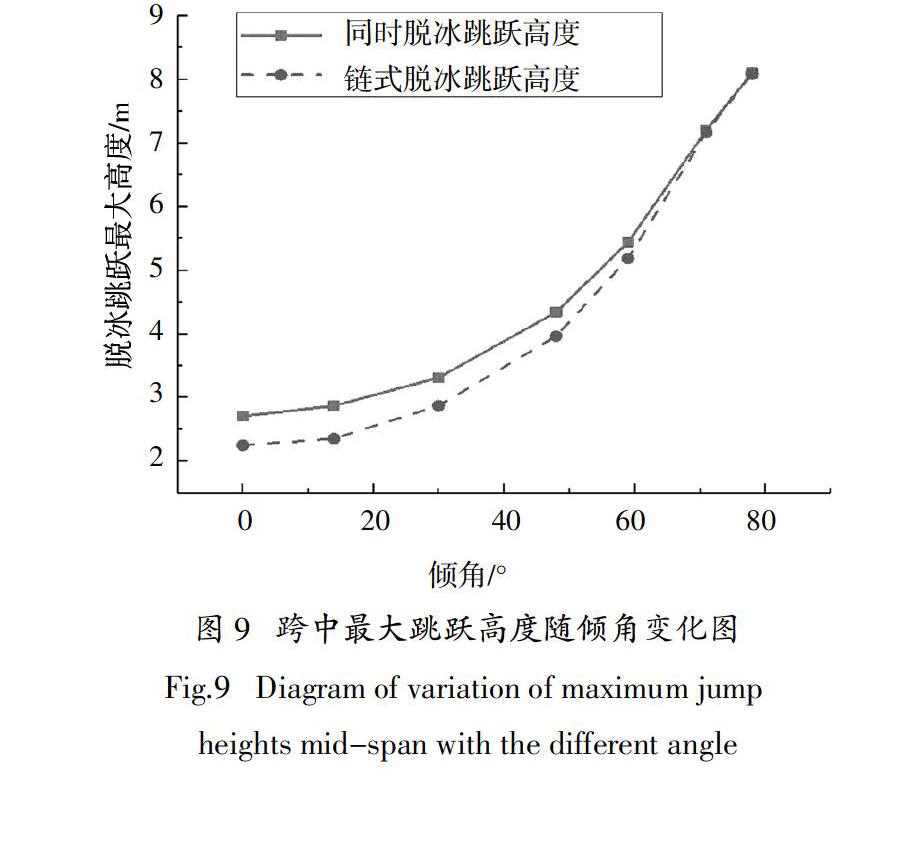
由圖9可知，當保持輸電線的初應力和覆冰厚度為10 mm不變時，跨中最大跳躍高度隨著高差的增大近似成指數增大;這里再次驗證了同時脫冰的最大跳躍高度是大于鏈式脫冰的最大跳躍高度，同時從圖中的分析還可以知道，隨著高差的增大，鏈式脫冰的跨中最大跳躍高度逐漸逼近同時脫冰的最大跳躍高度.

在前面所述基礎上又分別研究了在有高差和無高差情況下，覆冰厚度和初張力對覆冰后垂度和脫冰跳躍高度的影響，如圖10和圖11所示. 當覆冰厚度較大或者初張力較大時，不論是有高差還是沒有高差都會出現脫冰跳躍的高度大于覆冰后的垂度的情況，也就是輸電線出現上翻的情況，但是同樣條件下有高差造成的上翻情況更加危險;當覆冰厚度較大或者初張力較大時，覆冰后的垂度與鏈式脫冰跳躍的高度差值在有高差時明顯要大，同時增長要快，所以高差會加劇脫冰跳躍的上翻，就更容易造成輸電線的短線閃絡情況，給電網的安全帶來嚴重的隱患，所以在進行輸電線路設計中要考慮高差帶來的影響，減少不必要的危險發生.

5 ? 結論

輸電線路脫冰振動是輸電線路的一大威脅.實際工程中輸電線路脫冰是基于鏈式脫冰，并往往存在大高差.本文基于Ansys軟件，在采用殺死冰單元方法模擬并驗證的基礎上，研究了覆冰輸電線路鏈式脫冰情況下的響應及高差對脫冰的影響，得出了以下結論：

1）同時脫冰和鏈式脫冰模擬和試驗結果吻合較好，證明模擬的準確性.

2）等高差鏈式脫冰下，隨著脫冰速度的增大，脫冰跳躍最大位移先增大，然后趨于不變.導線的軸力與脫冰速度無關.

3）初應力不變情況下，跨中的脫冰跳躍最大高度隨著高差的增大近似指數增大，鏈式脫冰最大跳躍高度隨著高差增大逐漸逼近同時脫冰的最大跳躍高度.

4）當覆冰厚度較大或者初張力較大時，都會出現輸電線的上翻情況（跳躍高度大于覆冰后垂度），高差的存在加劇了上翻情況的發生，需要在設計中加以考慮.

參考文獻

[1] ? ?FARZANEH M. Atmospheric icing of power networks [M]. Berlin：Springer，2008：1—29.

[2] ? ?蔣興良，易輝.輸電線路覆冰及防護[M].北京：中國電力出版社，2002：1—57.

JIANG X L，YI H. Ice-coating and prevention of transmission line [M]. Beijing：China Electric Power Press，2002：1—57. （In Chinese）

[3] ? ?肖錫武，楊軍，DRUEZ J，等. 懸垂纜線的非線性振動[J]. 振動：測試與診斷，2003，23（2）：110—113.

XIAO X W，YANG J，DRUEZ J，et al. Nonlinear oscillations of a suspended cable[J].Journal of Vibration Measurement & Diagnosis，2003，23（2）：110—113.（In Chinese）

[4] ? ?侯鐳，王黎明，朱普軒，等. 特高壓線路覆冰脫落跳躍的動力計算[J]. 中國電機工程學報，2008，28（6）：1—6.

HOU L，WANG L M，ZHU P X，et al. Dynamic behavior computation of ice shedding of UHV overhead transmission lines [J].Proceedings of the CSEE，2008，28（6）：1—6. （In Chinese）

[5] ? ?晏致濤，張海峰，李正良. 基于增量諧波平衡法的覆冰輸電線舞動分析[J]. 振動工程學報，2012，25（2）：161—165.

YAN Z T，ZHANG H F，LI Z L. Galloping analysis of iced transmission lines based on incremental harmonic balance method [J].Journal of Vibration Engineering，2012，25（2）：161—166. （In Chinese）

[6] ? ?JAMALEDDINE A，MCCLUREl G，ROUSSELET J. Simulation ?of ?ice-shedding ?on ?electrical ?transmission ?lines ?using ?ADINA [J] . Computers and Structures，1993，47（4/5）：523—536.

[7] ? ?LASZLO E，FARZANEH M. Vibration of bundled conductors following ice shedding [J]. IEEE Transactions on Power Delivery，2008，23（2）：1097—1104.

[8] ? ?李永平，蘇攀，鄭毅. 架空導線覆冰及脫冰的數值模擬研究[J].水電能源科學，2010，28（12）：133—135.

LI Y P，SU P，ZHENG Y. Research on icing and ice-shedding numerical simulation of overhead conductors [J]. Water Resources and Power，2010，28（12）：133—135. （In Chinese）

[9] ? ?魯元兵，樓文娟，李煥龍. 輸電導線不均勻脫冰的全過程模擬分析[J]. 振動與沖擊，2010，29（9）：47—50.

LU Y B，LOU W J，LI H L. Whole process analysis for non-uniform ice shedding of transmission lines [J]. Journal of Vibration and Shock，2010，29（9）：47—50. （In Chinese）

[10] ?王昕，樓文娟. 多跨輸電線路脫冰動力響應研究[J].工程力學，2011，28（1）：226—232.

WANG X，LOU W J. Dynamic response analysis of multi-span transmission line to ice-shedding shock [J]. Engineering Mechanics，2011，28（1）：226—232. （In Chinese）

[11] ?劉和云. 架空線覆冰和脫冰機理的研究[D].武漢：華中科技大學，2001：1—60.

LIU H Y. Theories and applications of ice-coating and its prevention on overhead transmission line [D]. Wuhan：Huazhong University of Science and Technology，2001：1—60. （In Chinese）

[12] ?李黎，張行，尹鵬.大跨越輸電線路脫冰跳躍反應的控制研究[J]. 振動與沖擊，2008，27（10）：61—64.

LI L，ZHANG X，YIN P. Investigation on control over leap of long span transmission line due to ice-shedding shock [J]. Journal of Vibration and Shock，2008，27（10）：61—64. （In Chinese）

[13] ?杜運興，盧心龍.輸電塔線體系風致覆冰脫落動力響應的研究[J].湖南大學學報（自然科學版），2015，42（11）：88—94.

DU Y X，LU X L. Research on dynamic response of ice wind-induced ice-shedding of transmission tower-line system [J].Journal of Hunan University （Natural Sciences），2015，42（11）：88—94. （In Chinese）

[14] ?杜運興，盧心龍，聶逸悠. 線路覆冰分層脫落動力響應的研究[J]. 湖南大學學報（自然科學版），2017，44（7）：104—110.

DU Y X，LU X L，NIE Y Y. Research on dynamic response of ice layer shedding in line system [J].Journal of Hunan University（Natural Sciences），2017，44（7）：104—110. （In Chinese）

[15] ?王璋奇，王劍，齊立忠. 同期脫冰架空輸電導線的動張力特性實驗研究[J]. 噪聲與振動控制，2016，36（1）：157—162.

WANG Z Q，WANG J，QI L Z. Experimental study on the dynamic tension characteristics of the overhead transmission conductor under synchronous ice shedding [J]. Noise and Vibration Control，2016，36（1）：157—162. （In Chinese）

[16] ?王璋奇，齊立忠，王劍，等. 架空輸電線非同期脫冰跳躍動張力實驗研究[J]. 振動與沖擊，2016，35（22）：61—65.

WANG Z Q，QI L Z，WANG J，et al. Experiments on the dynamic tension of an overhead conductor under the asynchronous ice shedding [J].Journal of Vibration and Shock，2016，35（22）：61—65. （In Chinese）

[17] ?沈國輝，袁光輝，孫炳楠，等. 考慮脫冰速度效應的輸電線路脫冰模擬[J]. 重慶大學學報，2010，33（9）：132—138.

SHEN H，YUAN G H，SUN B N，et al. Simulation of ice-shedding on transmission lines considering ice-shedding velocity effect[J].Journal of Chongqing University，2010，33（9）：132—138. （In Chinese）

[18] ?陳科全，嚴波，郭躍明，等. 超高壓輸電線脫冰動力響應數值模擬[J]. 重慶大學學報，2009，32（11）：1306—1310.

CHEN K Q，YAN B，GUO Y M，et al. Dynamic responses of ultra-high voltage transmission line ice shedding [J].Journal of Chongqing University，2009，32（11）：1306—1310. （In Chinese）

[19] ?ZHANG Q，POPPLEWELL N，SHAH A H. Galloping of bundle conductor[J]. Journal of Sound and Vibration，2000，234（1）：115—134.